"If a tree falls in the forest, and no one hears it, does it make a sound?" I remember seeing an actual argument get started on this subject—a fully naive argument that went nowhere near Berkeleyan subjectivism. Just:
"It makes a sound, just like any other falling tree!"
"But how can there be a sound that no one hears?"
The standard rationalist view would be that the first person is speaking as if "sound" means acoustic vibrations in the air; the second person is speaking as if "sound" means an auditory experience in a brain. If you ask "Are there acoustic vibrations?" or "Are there auditory experiences?", the answer is at once obvious. And so the argument is really about the definition of the word "sound".
I think the standard analysis is essentially correct. So let's accept that as a premise, and ask: Why do people get into such an argument? What's the underlying psychology?
A key idea of the heuristics and biases program is that mistakes are often more revealing of cognition than correct answers. Getting into a heated dispute about whether, if a tree falls in a deserted forest, it makes a sound, is traditionally considered a mistake.
So what kind of mind design corresponds to that error?
In Disguised Queries I introduced the blegg/rube classification task, in which Susan the Senior Sorter explains that your job is to sort objects coming off a conveyor belt, putting the blue eggs or "bleggs" into one bin, and the red cubes or "rubes" into the rube bin. This, it turns out, is because bleggs contain small nuggets of vanadium ore, and rubes contain small shreds of palladium, both of which are useful industrially.
Except that around 2% of blue egg-shaped objects contain palladium instead. So if you find a blue egg-shaped thing that contains palladium, should you call it a "rube" instead? You're going to put it in the rube bin—why not call it a "rube"?
But when you switch off the light, nearly all bleggs glow faintly in the dark. And blue egg-shaped objects that contain palladium are just as likely to glow in the dark as any other blue egg-shaped object.
So if you find a blue egg-shaped object that contains palladium, and you ask "Is it a blegg?", the answer depends on what you have to do with the answer: If you ask "Which bin does the object go in?", then you choose as if the object is a rube. But if you ask "If I turn off the light, will it glow?", you predict as if the object is a blegg. In one case, the question "Is it a blegg?" stands in for the disguised query, "Which bin does it go in?". In the other case, the question "Is it a blegg?" stands in for the disguised query, "Will it glow in the dark?"
Now suppose that you have an object that is blue and egg-shaped and contains palladium; and you have already observed that it is furred, flexible, opaque, and glows in the dark.
This answers every query, observes every observable introduced. There's nothing left for a disguised query to stand for.
So why might someone feel an impulse to go on arguing whether the object is really a blegg?
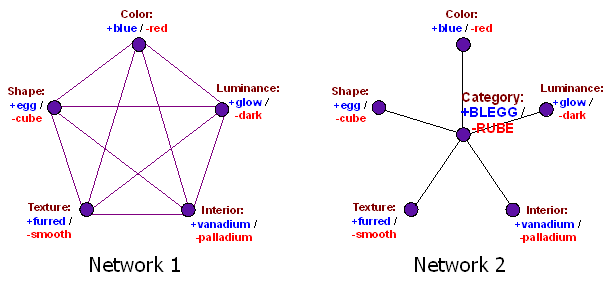
This diagram from Neural Categories shows two different neural networks that might be used to answer questions about bleggs and rubes. Network 1 has a number of disadvantages—such as potentially oscillating/chaotic behavior, or requiring O(N2) connections—but Network 1's structure does have one major advantage over Network 2: Every unit in the network corresponds to a testable query. If you observe every observable, clamping every value, there are no units in the network left over.
Network 2, however, is a far better candidate for being something vaguely like how the human brain works: It's fast, cheap, scalable—and has an extra dangling unit in the center, whose activation can still vary, even after we've observed every single one of the surrounding nodes.
Which is to say that even after you know whether an object is blue or red, egg or cube, furred or smooth, bright or dark, and whether it contains vanadium or palladium, it feels like there's a leftover, unanswered question: But is it really a blegg?
Usually, in our daily experience, acoustic vibrations and auditory experience go together. But a tree falling in a deserted forest unbundles this common association. And even after you know that the falling tree creates acoustic vibrations but not auditory experience, it feels like there's a leftover question: Did it make a sound?
We know where Pluto is, and where it's going; we know Pluto's shape, and Pluto's mass—but is it a planet?
Now remember: When you look at Network 2, as I've laid it out here, you're seeing the algorithm from the outside. People don't think to themselves, "Should the central unit fire, or not?" any more than you think "Should neuron #12,234,320,242 in my visual cortex fire, or not?"
It takes a deliberate effort to visualize your brain from the outside—and then you still don't see your actual brain; you imagine what you think is there, hopefully based on science, but regardless, you don't have any direct access to neural network structures from introspection. That's why the ancient Greeks didn't invent computational neuroscience.
When you look at Network 2, you are seeing from the outside; but the way that neural network structure feels from the inside, if you yourself are a brain running that algorithm, is that even after you know every characteristic of the object, you still find yourself wondering: "But is it a blegg, or not?"
This is a great gap to cross, and I've seen it stop people in their tracks. Because we don't instinctively see our intuitions as "intuitions", we just see them as the world. When you look at a green cup, you don't think of yourself as seeing a picture reconstructed in your visual cortex—although that is what you are seeing—you just see a green cup. You think, "Why, look, this cup is green," not, "The picture in my visual cortex of this cup is green."
And in the same way, when people argue over whether the falling tree makes a sound, or whether Pluto is a planet, they don't see themselves as arguing over whether a categorization should be active in their neural networks. It seems like either the tree makes a sound, or not.
We know where Pluto is, and where it's going; we know Pluto's shape, and Pluto's mass—but is it a planet? And yes, there were people who said this was a fight over definitions—but even that is a Network 2 sort of perspective, because you're arguing about how the central unit ought to be wired up. If you were a mind constructed along the lines of Network 1, you wouldn't say "It depends on how you define 'planet'," you would just say, "Given that we know Pluto's orbit and shape and mass, there is no question left to ask." Or, rather, that's how it would feel—it would feel like there was no question left—if you were a mind constructed along the lines of Network 1.
Before you can question your intuitions, you have to realize that what your mind's eye is looking at is an intuition—some cognitive algorithm, as seen from the inside—rather than a direct perception of the Way Things Really Are.
People cling to their intuitions, I think, not so much because they believe their cognitive algorithms are perfectly reliable, but because they can't see their intuitions as the way their cognitive algorithms happen to look from the inside.
And so everything you try to say about how the native cognitive algorithm goes astray, ends up being contrasted to their direct perception of the Way Things Really Are—and discarded as obviously wrong.
Silas, let me try to give you a little more explicit answer. This is how I think it is meant to work, although I agree that the description is rather unclear.
Each dot in the diagram is an "artificial neuron". This is a little machine that has N inputs and one output, all of which are numbers. It also has an internal "threshold" value, which is also a number. The way it works is it computes a "weighted sum" of its N inputs. That means that each input has a "weight", another number. It multplies weight 1 times input 1, plus weight 2 times input 2, plus weight 3 times input 3, and so on, to get the weighted sum. (Note that weights can also be negative, so some inputs can lower the sum.) It then compares this with the threshold value. If the sum is greater than the threshold, it outputs 1, otherwise it outputs 0. If a neuron's output is a 1 we say it is "firing" or "activated".
The diagram shows how the ANs are hooked up into a network, an ANN. Each neuron in Figure 1 has 5 inputs. 4 of them come from the other 4 neurons in the circuit and are represented by the lines. The 5th comes from the particular characteristic which is assigned to that neuron, i.e. color, luminance, etc. If the object has that property, that 5th input is a 1, else a 0. All of the connections in this network are bidirectional, so that neuron 1 receives input from neuron 2, while neuron 2 receives input from neuron 1, etc.
So to think about what this network does, we imagine inputting the 5 qualities which are observed about an object to the "5th" input of each of the 5 neurons. We imagine that the current output levels of all the neurons are set to something arbitrary, let's just say zero. And perhaps initially the weights and threshold values are also quite random.
When we give the neurons this activation pattern, some of them may end up firing and some may not, depending on how the weights and thresholds are set up. And once a neuron starts firing, that feeds into one of the inputs of the other 4 neurons, which may change their own state. That feeds back through the network as well. This may lead to oscillation or an unstable state, but hopefully it will settle down into some pattern.
Now, according to various rules, we will typically adjust the weights. There are different ways to do this, but I think the concept in this example is that we will try to make the output of each neuron match its "5th input", the object characteristic assigned to that neuron. We want the luminance neuron to activate when the object is luminous, and so on. So we increase weights that will tend to move the output in that direction, decrease weights that would move it the other way, tweak the thresholds a bit. We do this repeatedly with different objects, making small changes to the weights - this is "training" the network. Eventually it hopefully settles down and does pretty much what we want it to.
Now we can give it some wrong or ambiguous inputs, and ideally it will still produce the output that is supposed to go there. If we input 4 of the characteristics of a blegg, the 5th neuron will also show the blegg-style output. It has "learned" the characteristics of bleggs and rubes.
In the case of Network 2, the setup is simpler - each edge neuron has just 2 inputs: its unique observed characteristic, and a feedback value from the center neuron. Each one performs its weighted-sum trick and sends its output to the center one, which has its own set of weights and a threshold that determines whether it activates or not. In this case we want to teach the center one to distinguish bleggs from rubes, so we would train it that way - adjusting the weights a little bit at a time until we find it firing when it is a blegg but not when it is a rube.
Anyway, I know this is a long explanation but I didn't see anyone else making it explicit. Hopefully it is mostly correct.