Diego Caples (diego@activated-ai.com)
Rob Neuhaus (rob@activated-ai.com)
Introduction
In principle, neuron activations in a transformer-based language model residual stream should be about the same scale. In practice, the dimensions unexpectedly widely vary in scale. Mathematical theories of the transformer architecture do not predict this. They expect no dimension to be more important than any other. Is there something wrong with our reasonably informed intuitions of how transformers work? What explains these outlier channels?
Previously, Anthropic researched the existence of these privileged basis dimensions (dimensions more important / larger than expected) and ruled out several causes. By elimination, they reached the hypothesis that per-channel normalization in the Adam optimizer was the cause of privileged basis. However, they did not prove this was the case.
We conclusively show that Adam causes outlier channels / privileged basis within the transformer residual stream. When replacing the Adam optimizer with SGD, models trained do not have a privileged residual stream.
As a whole, this work improves mechanistic understanding of transformer LM training dynamics and confirms that our mathematical models of transformers are not flawed. Rather, they simply do not take into account the training process.
Our code is open source at the LLM outlier channel exploration GitHub.
Key Results
- Training an LM with SGD does not result in a privileged basis, indicating that Adam is the cause of privileged basis in transformer LMs.
- Training a 12M parameter model on TinyStories allows us to replicate outlier channel behavior on a small LM, training in less than 15 minutes on an H100.
Background
Recommended Reading
- Privileged Bases in the Transformer Residual Stream
- Toy Models of Superposition (Privileged Basis Section)
More About Anthropic’s Work
We consider Anthropic’s research on privileged basis the primary motivator for this work. In Anthropic’s Privileged Bases in the Transformer Residual Stream, they demonstrate privileged basis in a 200M parameter LLM, performed some experiments to rule out possible causes, but did not find a definitive cause. They hypothesize that outlier channels are caused by Adam’s lack of rotational equivariance, and suggest that training using SGD could isolate Adam as the cause.
Adam vs SGD, and Rotational Equivariance
Consider an experiment where we rotate the parameter space of a neural network, train it, and then invert the rotation. With Stochastic Gradient Descent (SGD), this process yields the same model as if we hadn't rotated at all. However, with the Adam optimizer, we end up with a different model.
This difference can be explained by the presence/absence a property called rotational equivariance. SGD is rotationally equivariant: optimizer steps are always directly proportional to the gradient of the loss function, regardless of the chosen coordinate system. In contrast, Adam is not rotationally equivariant because it takes steps in ways that are not proportional to the gradient. Updates depend on coordinate-wise gradient statistics. As we later show, this difference is what leads to privileged basis within LMs.
Kurtosis
Motivated by Anthropic, we use excess kurtosis as a metric for measuring basis privilege.
We encourage the reader to read Anthropic’s reasoning for why this is a good metric, but here we aim to demonstrate graphically that excess kurtosis is a reasonable choice for measuring basis privilege.
We plot the middle layer residual stream activations for the last token of string:
“Lilly saw a big red apple!”
as an Adam optimized LM training run progresses.
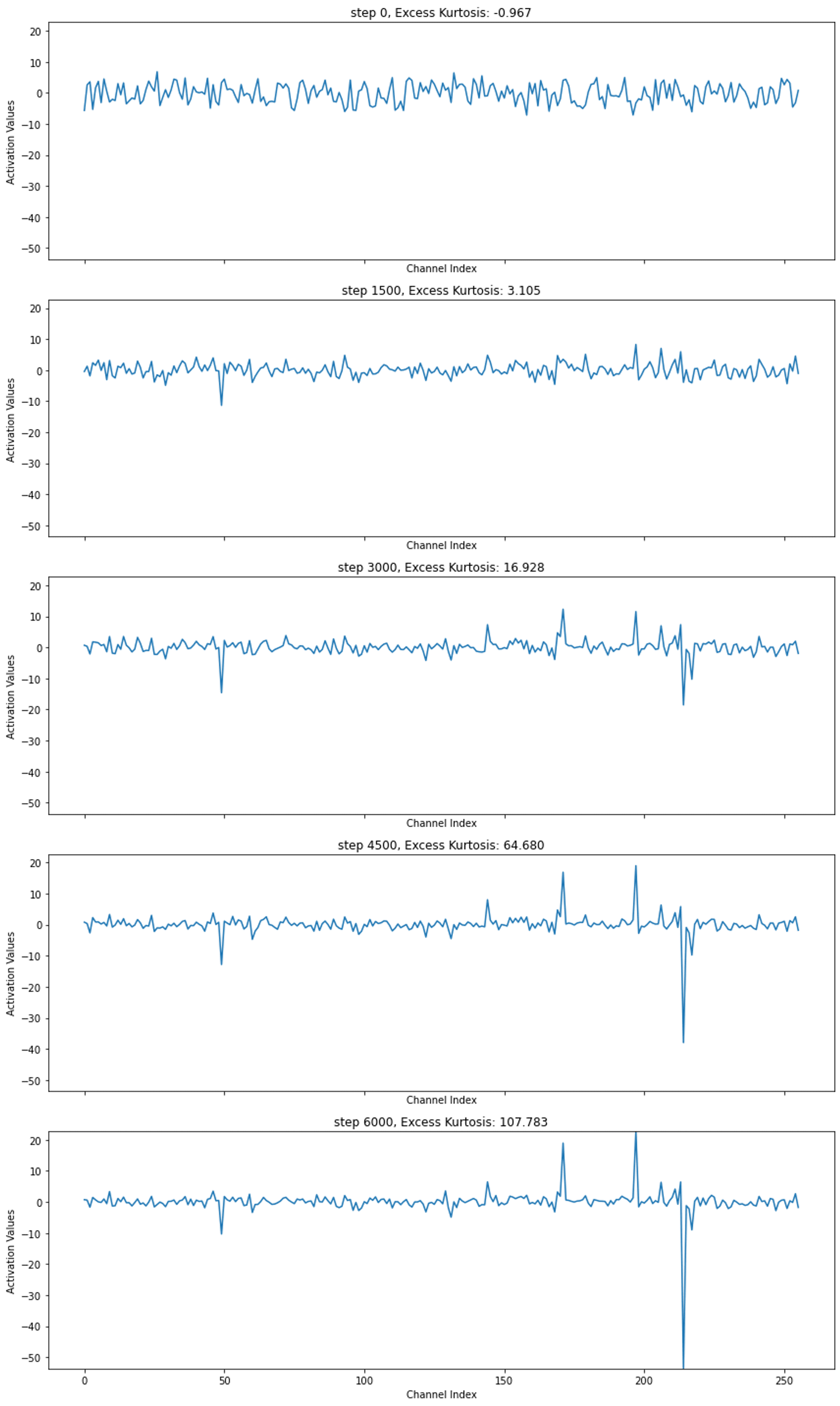
Note how as training progresses, the outlier channels in the activation become increasingly prominent. The excess kurtosis of the activations increases accordingly.
TinyStories
We use the TinyStories datasets in all of our experiments. TinyStories is a small, synthetically generated dataset of English children’s stories. The authors showed that ~10M parameter LMs trained on the dataset can generate coherent and creative stories, and demonstrate emergent properties previously only found in much larger LMs. This enables us to reproduce LMs with outlier channels at a much smaller scale than previous works.
Experiments
Replicating Outlier Channels at Small Scale
To test if training with SGD prevents privileged basis, we first need to have a model that replicates outlier channel behavior.
We train a 12M parameter transformer LM model with Adam. It is capable of generating coherent stories. As the model trains, the excess kurtosis increases, until it is over 100 by the time training terminates. Clear outlier channels are present (as seen in Model Excess Kurtosis through Training figure above).
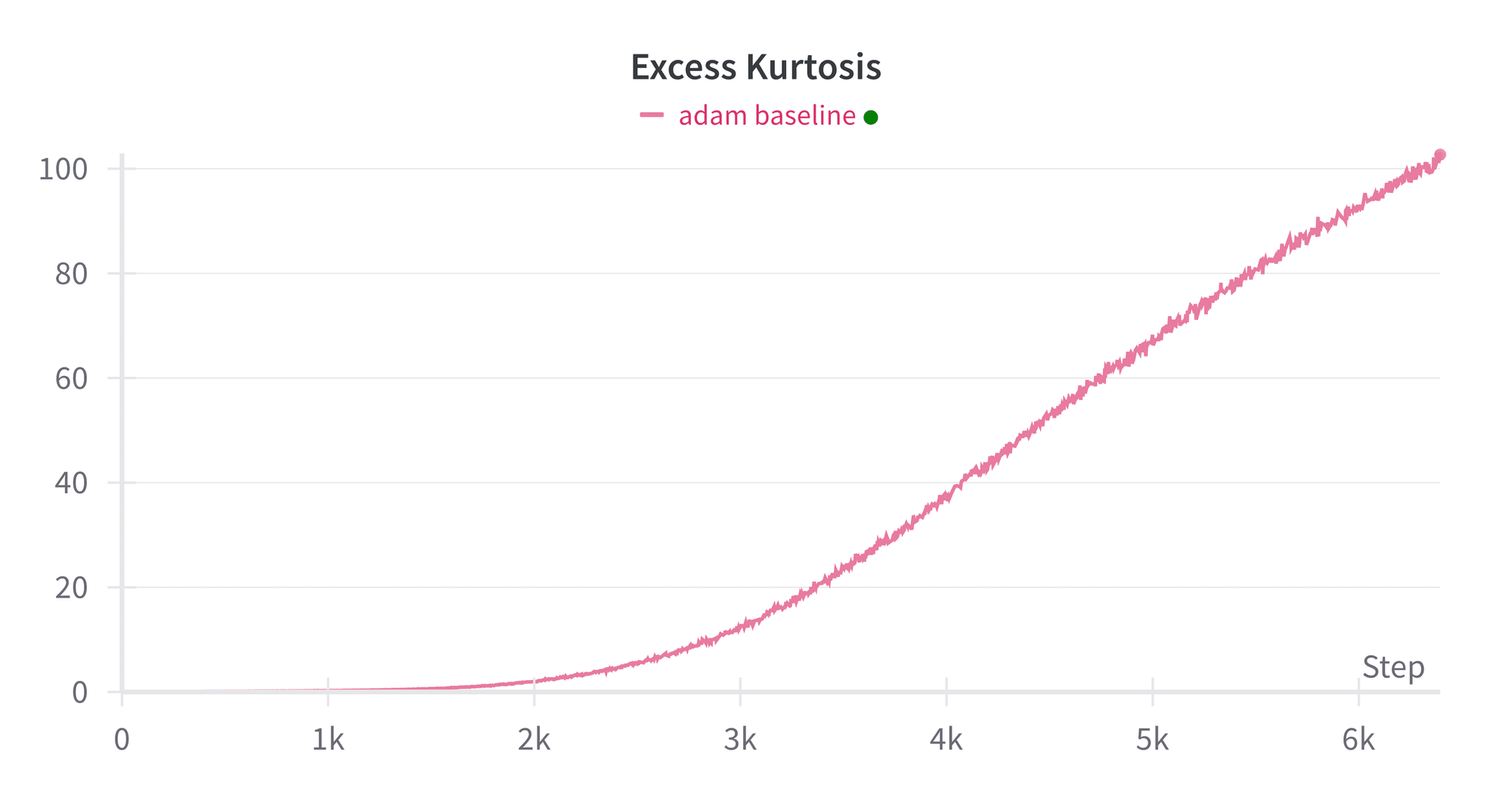
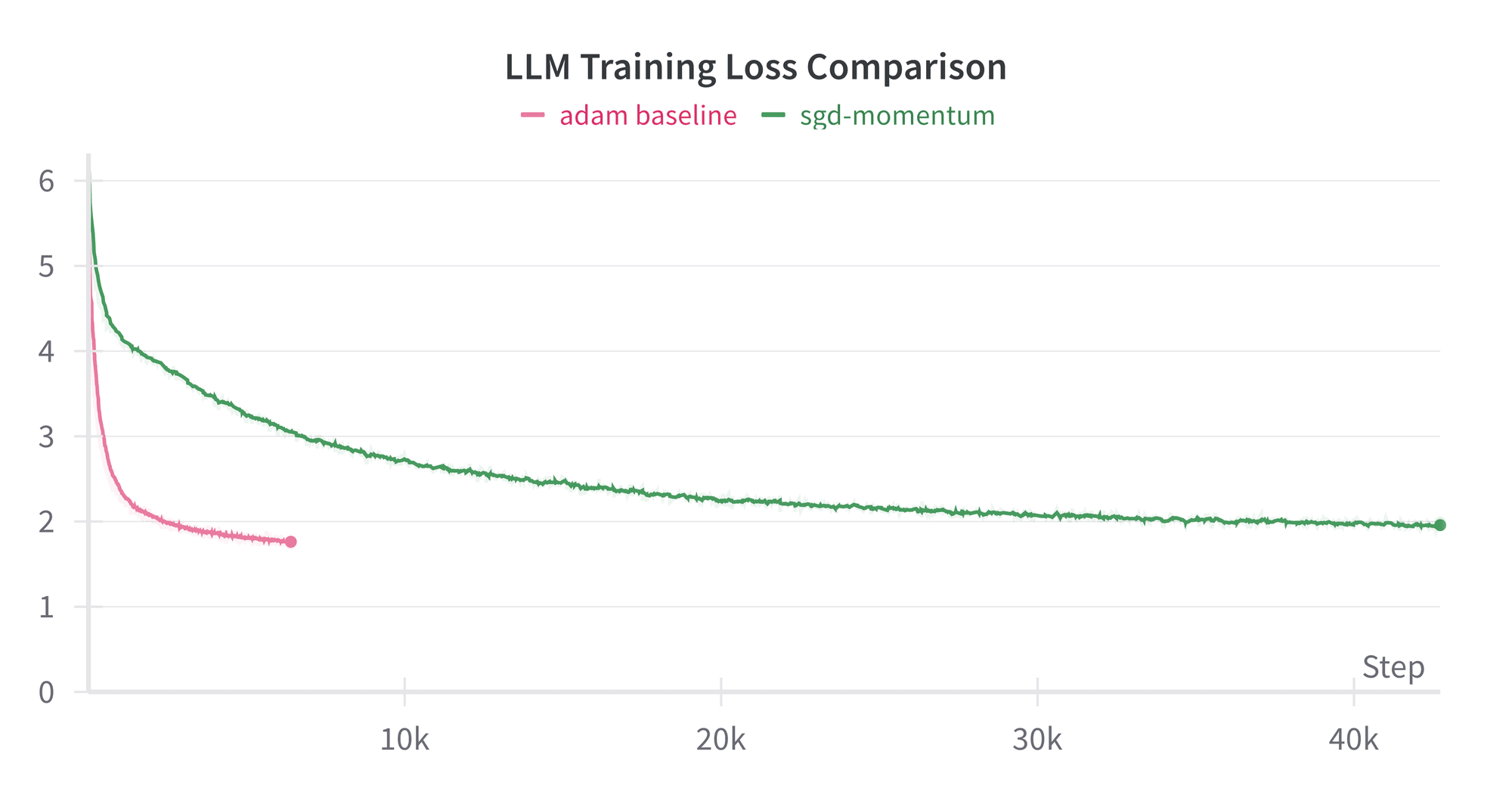
Training an LM with SGD
Next, we train the exact same model, this time using SGD with momentum (still rotationally equivariant). Adam takes ≈16x fewer steps to reach identical loss to SGD. It is the small size of the model which makes it affordable to train for so long.
Comparing the excess kurtosis of SGD and Adam shows a stark contrast:
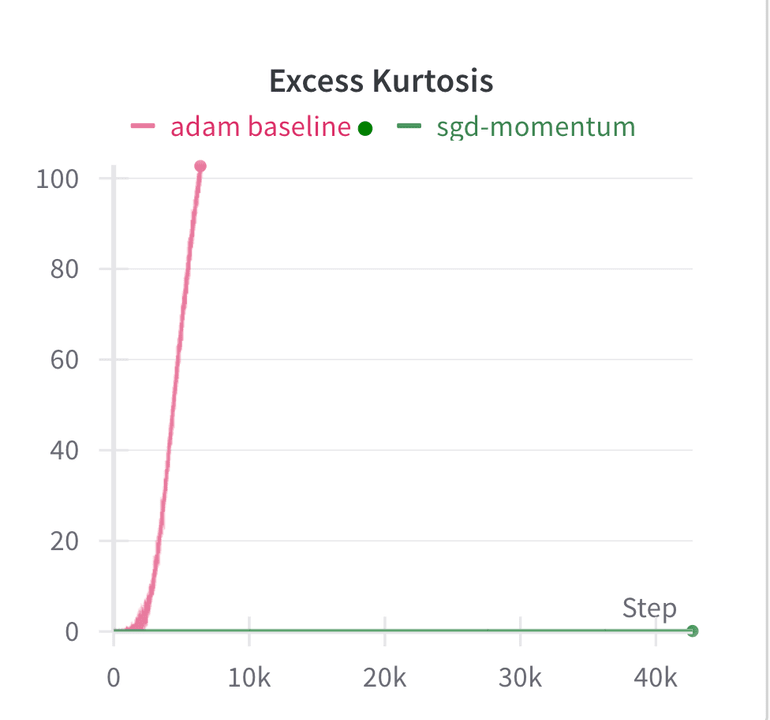
While the Adam-trained model’s excess kurtosis quickly exceeds 100, the excess kurtosis of the SGD trained model remains approximately 0 throughout training. It is clear that Adam is causally responsible for privileged basis/outlier channels.
Conclusions
We conclusively demonstrate that the Adam optimizer is the primary cause of privileged basis dimensions in transformer-based language models. By training identical 12M parameter models on the TinyStories dataset using both Adam and SGD with momentum, we observed a clear difference in the development of outlier channels:
- Models trained with Adam exhibited a rapid increase in excess kurtosis, reaching values over 100, indicating significant outlier channels.
- In contrast, models trained with SGD maintained an excess kurtosis close to 0 throughout the training process, demonstrating a lack of privileged basis dimensions.
These findings have several important implications:
- Our results confirm that the mathematical theories of transformer architecture, which predict no privileged basis in the residual stream, are not fundamentally flawed. The unexpected variation in residual stream dimension scales is a consequence of the optimization process rather than an inherent property of the transformer architecture.
- This work provides insight into the training dynamics of large language models, highlighting the impact that optimizer choice can have on the internal representations formed by these models.
- By replicating the outlier channel phenomenon in a small 12M parameter model, we've demonstrated that this behavior is not limited to larger models and can be studied more efficiently.
Future Research
- Use sparse autoencoders to see if learned features align with the outlier channels. We have some early evidence that this is the case.
- What are the exact mechanics within Adam that cause features to align with basis dimensions?
Cool work! This is the outcome I expected, but I'm glad someone actually went and did it