The AI in the quantum box

In the previous post, I discussed the example of an AI whose concept space and goals were defined in terms of classical physics, which then learned about quantum mechanics. Let's elaborate on that scenario a little more.

I wish to zoom in on a certain assumption that I've noticed in previous discussions of these kinds of examples. Although I couldn't track down an exact citation right now, I'm pretty confident that I've heard the QM scenario framed as something like "the AI previously thought in terms of classical mechanics, but then it finds out that the world actually runs on quantum mechanics". The key assumption being that quantum mechanics is in some sense more real than classical mechanics.

This kind of an assumption is a natural one to make if someone is operating on an AIXI-inspired model of AI. Although AIXI considers an infinite amount of world-models, there's a sense in which AIXI always strives to only have one world-model. It's always looking for the simplest possible Turing machine that would produce all of the observations that it has seen so far, while ignoring the computational cost of actually running that machine. AIXI, upon finding out about quantum mechanics, would attempt to update its world-model into one that only contained QM primitives and to derive all macro-scale events right from first principles.

No sane design for a real-world AI would try to do this. Instead, a real-world AI would take advantage of scale separation. This refers to the fact that physical systems can be modeled on a variety of different scales, and it is in many cases sufficient to model them in terms of concepts that are defined in terms of higher-scale phenomena. In practice, the AI would have a number of different world-models, each of them being applied in different situations and for different purposes.

Here we get back to the view of concepts as tools, which I discussed in the previous post. An AI that was doing something akin to reinforcement learning would come to learn the kinds of world-models that gave it the highest rewards, and to selectively employ different world-models based on what was the best thing to do in each situation.

As a toy example, consider an AI that can choose to run a low-resolution or a high-resolution psychological model of someone it's interacting with, in order to predict their responses and please them. Say the low-resolution model takes a second to run and is 80% accurate; the high-resolution model takes five seconds to run and is 95% accurate. Which model will be chosen as the one to be used will depend on the cost matrix of making a correct prediction, making a false prediction, and the consequence of making the other person wait for an extra four seconds before the AI's each reply.

We can now see that a world-model being the most real, i.e. making the most accurate predictions, doesn't automatically mean that it will be used. It also needs to be fast enough to run, and the predictions need to be useful for achieving something that the AI cares about.

World-models as tools

From this point of view, world-models are literally tools just like any other. Traditionally in reinforcement learning, we would define the value of a policy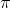 in state s as the expected reward given the state s and the policy ,

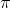but under the "world-models are tools" perspective, we need to also condition on the world-model m,

.

We are conditioning on the world-model in several distinct ways.

First, there is the expected behavior of the world as predicted by world-model m. A world-model over the laws of social interaction would do poorly at predicting the movement of celestial objects, if it could be applied to them at all. Different predictions of behavior may also lead to differing predictions of the value of a state. This is described by the equation above.

Second, there is the expected cost of using the world-model. Using a more detailed world-model may be more computationally expensive, for instance. One way of interpreting this in a classical RL framework would be that using a specific world-model will place the agent in a different state than using some other world-model. We might describe by saying that in addition to the agent choosing its next action a on each time-step, the agent also needs to choose the world-model m which it will use to analyze its next observations. This will be one of the inputs for the transition function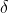 to the next state.

Third, there is the expected behavior of the agent using world-model m. An agent with different beliefs about the world will act differently in the future: this means that the future policy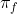 actually depends on the chosen world-model.

Some very interesting questions pop up at this point. Your currently selected world-model is what you use to evaluate your best choices for the next step... including the choice of what world-model to use next. So whether or not you're going to switch to a different world-model for evaluating the next step depends on whether your current world-model says that a different world-model would be better in that step.

We have not fully defined what exactly we mean by "world-models" here. Previously I gave the example of a world-model over the laws of social interaction, versus a world-model over the laws of physics. But a world-model over the laws of social interaction, say, would not have an answer to the question of which world-model to use for things it couldn't predict. So one approach would be to say that we actually have some meta-model over world-models, telling us which is the best to use in what situation.

On the other hand, it does also seem like humans often use a specific world-model and its predictions to determine whether to choose another world-model. For example, in rationalist circles you often see arguments to the line of, "self-deception might give you extra confidence, but it introduces errors into your world-model, and in the long term those are going to be more harmful than the extra confidence is beneficial". Here you see an implicit appeal to a world-model which predicts an accumulation of false beliefs with some specific effects, as well as predicting the extra self-esteem with its effects. But this kind of an analysis incorporates very specific causal claims from various (e.g. psychological) models, which are models over the world rather than just being part of some general meta-model over models. Notice also that the example analysis takes into account the way that having a specific world-model affects the state transition function: it assumes that a self-deceptive model may land us in a state where we have a higher self-esteem.

It's possible to get stuck in one world-model: for example, a strongly non-reductionist model evaluating the claims of a highly reductionist one might think it obviously crazy, and vice versa. So it seems that we do need something like a meta-evaluation function. Otherwise it would be too easy to get stuck in one model which claimed that it was the best one in every possible situation, and never agreed to "give up control" in favor of another one.

One possibility for such a thing would be a relatively model-free learning mechanism, which just kept track of the rewards accumulated when using a particular model in a particular situation. It would then bias the selection of the model towards the direction of the model that had been the most successful so far.

Human neuroscience and meta-models

We might be able to identify something like this in humans, though this is currently very speculative on my part. Action selection is carried out in the basal ganglia: different brain systems send the basal ganglia "bids" for various actions. The basal ganglia then chooses which actions to inhibit or disinhibit (by default, everything is inhibited). The basal ganglia also implements reinforcement learning, selectively strengthening or weakening the connections associated with a particular bid and context when a chosen action leads to a higher or lower reward than was expected. It seems that in addition to choosing between motor actions, the basal ganglia also chooses between different cognitive behaviors, likely even thoughts: 

If action selection and reinforcement learning are normal functions of the basal ganglia, it should be possible to interpret many of the human basal ganglia-related disorders in terms of selection malfunctions. For example, the akinesia of Parkinson's disease may be seen as a failure to inhibit tonic inhibitory output signals on any of the sensorimotor channels. Aspects of schizophrenia, attention deficit disorder and Tourette's syndrome could reflect different forms of failure to maintain sufficient inhibitory output activity in non-selected channels. Conseqently, insufficiently inhibited signals in non-selected target structures could interfere with the output of selected targets (expressed as motor/verbal tics) and/or make the selection system vulnerable to interruption from distracting stimuli (schizophrenia, attention deficit disorder). The opposite situation would be where the selection of one functional channel is abnormally dominant thereby making it difficult for competing events to interrupt or cause a behavioural or attentional switch. Such circumstances could underlie addictive compulsions or obsessive compulsive disorder. (Redgrave 2007)

Although I haven't seen a paper presenting evidence for this particular claim, it seems plausible to assume that humans similarly come to employ new kinds of world-models based on the extent to which using a particular world-model in a particular situation gives them rewards. When a person is in a situation where they might think in terms of several different world-models, there will be neural bids associated with mental activities that recruit the different models. Over time, the bids associated with the most successful models will become increasingly favored. This is also compatible with what we know about e.g. happy death spirals and motivated stopping: people will tend to have the kinds of thoughts which are rewarding to them.

The physicist and the AI

In my previous post, when discussing the example of the physicist who doesn't jump out of the window when they learn about QM and find out that "location" is ill-defined:

The physicist cares about QM concepts to the extent that the said concepts are linked to things that the physicist values. Maybe the physicist finds it rewarding to develop a better understanding of QM, to gain social status by making important discoveries, and to pay their rent by understanding the concepts well enough to continue to do research. These are some of the things that the QM concepts are useful for. Likely the brain has some kind of causal model indicating that the QM concepts are relevant tools for achieving those particular rewards. At the same time, the physicist also has various other things they care about, like being healthy and hanging out with their friends. These are values that can be better furthered by modeling the world in terms of classical physics. [...]

A part of this comes from the fact that the physicist's reward function remains defined over immediate sensory experiences, as well as values which are linked to those. Even if you convince yourself that the location of food is ill-defined and you thus don't need to eat, you will still suffer the negative reward of being hungry. The physicist knows that no matter how they change their definition of the world, that won't affect their actual sensory experience and the rewards they get from that.

So to prevent the AI from leaving the box by suitably redefining reality, we have to somehow find a way for the same reasoning to apply to it. I haven't worked out a rigorous definition for this, but it needs to somehow learn to care about being in the box in classical terms, and realize that no redefinition of "location" or "space" is going to alter what happens in the classical model. Also, its rewards need to be defined over models to a sufficient extent to avoid wireheading (Hibbard 2011), so that it will think that trying to leave the box by redefining things would count as self-delusion, and not accomplish the things it really cared about. This way, the AI's concept for "being in the box" should remain firmly linked to the classical interpretation of physics, not the QM interpretation of physics, because it's acting in terms of the classical model that has always given it the most reward. 

There are several parts to this.

1. The "physicist's reward function remains defined over immediate sensory experiences". Them falling down and breaking their leg is still going to hurt, and they know that this won't be changed no matter how they try to redefine reality.

2. The physicist's value function also remains defined over immediate sensory experiences. They know that jumping out of a window and ending up with all the bones in their body being broken is going to be really inconvenient even if you disregarded the physical pain. They still cannot do the things they would like to do, and they have learned that being in such a state is non-desirable. Again, this won't be affected by how they try to define reality.

We now have a somewhat better understanding of what exactly this means. The physicist has spent their entire life living in the classical world, and obtained nearly all of their rewards by thinking in terms of the classical world. As a result, using the classical model for reasoning about life has become strongly selected for. Also, the physicist's classical world-model predicts that thinking in terms of that model is a very good thing for surviving, and that trying to switch to a QM model where location was ill-defined would be a very bad thing for the goal of surviving. On the other hand, thinking in terms of exotic world-models remains a rewarding thing for goals such as obtaining social status or making interesting discoveries, so the QM model does get more strongly reinforced in that context and for that purpose.

Getting back to the question of how to make the AI stay in the box, ideally we could mimic this process, so that the AI would initially come to care about staying in the box. Then when it learns about QM, it understands that thinking in QM terms is useful for some goals, but if it were to make itself think in purely QM terms, that would cause it to leave the box. Because it is thinking mostly in terms of a classical model, which says that leaving the box would be bad (analogous to the physicist thinking mostly in terms of the classical model which says that jumping out of the window would be bad), it wants to make sure that it will continue to think in terms of the classical model when it's reasoning about its location.