It really is an important, well-written post, and I very much enjoyed it. I especially appreciate the twin studies example. I even think that something like that should maybe go into the wikitags, because of how often the title sentence appears everywhere? I'm relatively new to LessWrong though, so I'm not sure about the posts/wikitags distinction, maybe that's not how it's done here.

I have a pitch for how to make it even better though. I think the part about "when you have lots of data" vs "when you have less data" would be cleaner and more intuitive if it were rewritten as "when $X$ is discrete vs continuous". Now the first example (the "more data" one) uses a continuous $X$; thus, the sentence "define $y_i$ as the sample mean of $Y$ taken over all $y_j$ for which $x_j=x_i$" creates confusion, since it's literally impossible to get the same value from a truly continuous random variable twice; it requires some sort of binning or something, which, yes, you do explain later. So it doesn't really flow as a "when you have lots of data" case---nobody does that in practice with truly continuous $X$, no matter how much data (at least as far as I know).

Now say we have a discrete $X$: e.g., an observation can come from classes A, B, or C. We have a total of $n$ observations, $n_j$ from class $j$. Turning the main spiel into numbers becomes straightforward:

On average, over all different values of $X$ weighted by their probability, the remaining variance in $Y$ is $1-p$ times the total variance in $Y$.

• "Over all different values of $X$" -> which we have three of;
• "weighted by their probability" -> we approximate the true probability of belonging to class $j$ as $\frac{n_j}{n}$, obviously;
• "the remaining variance in $Y$" for class $j$ is $\widehat{{Var}_j}=\frac{1}{n_j-1}{\sum }_{i=1}^{n_j}(y_{ij}-\overline{y_j}{)}^2$, also obviously. And we are done, no excuses or caveats needed! The final formula becomes: 

An example: $(Y\mid X)\sim N({\mu }_X,{\sigma }_X)$. Since we are creating the model, we know the true "platonic" explained variance. In this example, it's about 0.386. An estimated explained variance on an $n=200$ sample came out as 0.345 (code)

After that, we can say that directly approximating the variance of $Y\mid X$ for every value of a continuous $X$ is impossible, so we need a regression model.

And also that way it prepares the reader for the twin study example, which then can be introduced as a discrete case with each "class" being a unique set of genes, where $n_j$ always equals two.

If you do decide that it's a good idea, but don't feel like rewriting it, I guess we can go colab on the post and I can write that part. Anyway, please let me know your thoughts if you feel like it.

Is it correct to say that the mean is a good estimator whenever the variance is finite?

Well, yes, in the sense that the law of large numbers applies, i.e. 

The condition for that to hold is actually weaker. If all the $x_i$ are not only drawn from the same distribution, but are also independent, the existence of a finite $E\left[X\right]$ is necessary and sufficient for the sample mean to converge in probability to $E\left[X\right]$ as $n$ goes to infinity, if I understand the theorem correctly (I can't prove that yet though; the proof with a finite variance is easy). If $x_i$ aren't independent, the necessary condition is still weaker than the finite variance, but it's cumbersome and impractical, so finite variance is fine I guess.

But that kind of isn't enough to always justify the use of a sample mean as an estimator in practice? As foodforthought says, for a normal distribution it's simultaneously the lowest MSE estimator, the maximum likelihood estimator, and is an unbiased estimator, but that's not true for other distributions.

A quick example: suppose we want to determine the parameter $p$ of a Bernoulli random variable, i.e. "a coin". The prior distribution over $p$ is uniform; we flip the coin $n=10$ times, and use the sample success rate, $\frac{k}{n}$, i.e. the mean, i.e. the maximum likelihood estimate. Per simulation the mean squared error $E\left[{(\frac{k}{n}-p)}^2\right]$ is about 0.0167. However, if we use $\frac{k+1}{n+2}$ instead, the mean squared error drops to 0.0139 (code).

Honestly though, all of this seems like a frequentist cockamamie to me. We can't escape prior distributions; we may as well stop pretending that they don't exist. Just calculate a posterior and do whatever you want with it. E.g., how did I come up with the $\frac{k+1}{n+2}$ example? Well, it's the expected value of the posterior beta distribution for $p$ if the prior is uniform, so it also gives a lower MSE.

Consequently, we obtain

$$1-p=\frac{{\sum }_{i=1}^N(y_i-y_i^{\prime }{)}^2}{{\sum }_{i=1}^N(y_i-\overline{y}{)}^2+(y_i^{\prime }-\overline{y}{)}^2}.$$

Technically, we should also apply Bessel's correction to the denominator, so the right-hand side should be multiplied by a factor of $(1-\frac{1}{2N})$. Which is negligible for any sensible $N$, so doesn't really matter I guess.

Well, here ya go. Apparently, the mirror-test shrimp are Myrmica ants.

The article is named Are Ants (Hymenoptera, Formicidae) capable of self recognition?, and the abstract could've been "Yes" if the authors were fond of brevity (link: https://www.journalofscience.net/html/MjY4a2FsYWk=, link to a pdf: https://www.journalofscience.net/downnloadrequest/MjY2a2FsYWk=).

I remember hearing a claim that the mirror test success rate reported in this article is the highest among all animals ever tested, but this needs checking, can easily be false.

This is quite an extraordinary claim published in a terrible journal. I'm not sure how seriously I should take the results, but as far as I know nobody took them seriously enough to reproduce, which is a shame. I might do it one day.

Well, EB article you linked doesn't state directly that fatty acids are made out of carbon atoms linked via hydrogen bonds. It has two sentences relevant to the topic, and I am not entirely sure how to parse them:

Unsaturated fat, a fatty acid in which the hydrocarbon molecules have two carbons that share double or triple bond(s) and are therefore not completely saturated with hydrogen atoms. Due to the decreased saturation with hydrogen bonds, the structures are weaker and are, therefore, typically liquid (oil) at room temperature.

The first sentence is (almost)^[1] correct.

The second sentence, if viewed without the first one, may technically also be correct, but for what I know it's not and also it's not what they meant. See, fatty acids are capable of forming actual hydrogen bonds with each other with their "acid" parts (attached the picture from my organic chem course). On the left covalent bonds are shown with solid lines and hydrogen bonds are shown with dashed lines. The "fatty" part of the molecule is hidden under the letter R. On the right there is methyl instead of R (ie it's vinegar) and hydrogen bonds are not shown—molecules are just oriented in the right way. (I'm really sorry if I'm overexplaining, I just want to make it understandable for people with different backgrounds).

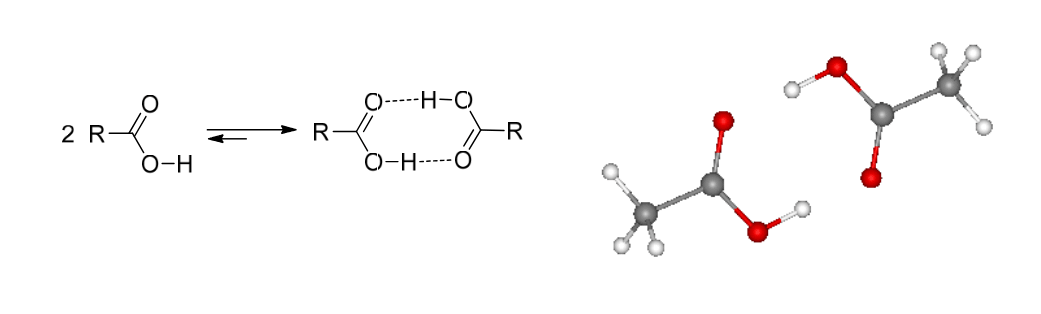
So, if interpreted literally, the second sentence states that unsaturated fatty acids form less hydrogen bonds with each other for whatever reason, and that's why they are liquid instead of solid. The explanation I've heard many times is different, it says that they are liquid because their "fatty" part is bent because double bonds have different geometry, so it is harder for them to form a crystal. I mean, it is still possible that they also form less hydrogen bonds, but I bet it's insignificant even if true.

But it honestly looks like they don't mean all of that at all, they are just incorrectly calling covalent bonds between carbon and hydrogen "hydrogen bonds" and they also don't know what they mean by "the structures are weaker". It's still a sin, but not the one you are accusing them of.

I am also completely fine with the phrasing that is currently in the article and I'm sorry for wasting your time with all that overthinking, hope it wasn't totally useless.

1. ^{^}

   The "fatty" part of a fatty acid molecule can't be called a "hydrocarbon molecule" since it is, well, a part of another molecule, and should rather be called "hydrocarbyl group" (see eg Wikipedia). Also the article should say "at least two carbons" instead of "two carbons" because, as this post is well aware, there exist polyunsaturated fatty acids.

Great post, enjoyed it!

A technical mistake here: "Fat is made of fatty acids—chains of carbon atoms linked via hydrogen bonds". They are linked via covalent bonds, not hydrogen bonds.

For those who don't know: covalent bond is a strong chemical bond that forms when two atoms provide one electron each to form an electron pair. These are normal bonds that hold molecules together. They are shown as sticks when one draws a molecule. Hydrogen bond is a much weaker intermolecular bond that forms when one molecule has an atom with an unshared electron pair and the other has a hydrogen atom that sort-of has an orbital to fit this electron pair.

And also having a chain of carbon atoms is about "fatty" part, and the "acid" part means that at the end of this chain there is a carboxyl group. I know that's not the point of this post, it just hurts a little, I'm sorry.