Many thanks to Michael Hanna and Joshua Batson for useful feedback and discussion. Kat Dearstyne and Kamal Maher conducted experiments during the SPAR Fall 2025 Cohort. TL;DR Cross-layer transcoders (CLTs) enable circuit tracing that can extract high-level mechanistic explanations for arbitrary prompts and are emerging as general-purpose infrastructure for mechanistic...
TLDR: recently, we wrote a paper proposing several evaluations of SAEs against "ground-truth" features computed w/ supervision for a given task (in our case, IOI [1]). However, we didn't optimize the SAEs much for performance in our tests. After putting the paper on arxiv, Alex carried out a more exhaustive...
Produced as part of the SERI ML Alignment Theory Scholars Program - Summer 2023 Cohort We would like to thank Atticus Geiger for his valuable feedback and in-depth discussions throughout this project. tl;dr: Activation patching is a common method for finding model components (attention heads, MLP layers, …) relevant to...
Thanks for your thoughtful comment! I think that's an interesting idea. If a replacement model is faithful, you would indeed expect it to behave similar when tested on other data. This may possibly connect to a related finding that we couldn't yet explain: that CLTs fail for memorized sequences, when those should be the simplest. Maybe the OOD test is something that we could do in real LLMs as well, not just toy models.
I don't think I'd go as far as saying "faithfulness==OOD generalization" though. I think it is possible that two different circuits produce the same behavior, even on OOD. For example, let model A and B learn to multiplicate arbitrary numbers perfectly. There are different ways to do x * y, for example compute +x y times, do it like we learned in school, etc. In those cases, OOD examples would still deliver equal output but the internal circuits are different. So I'd say that faithfulness is a stronger claim than OOD generalization.
Many thanks to Michael Hanna and Joshua Batson for useful feedback and discussion. Kat Dearstyne and Kamal Maher conducted experiments during the SPAR Fall 2025 Cohort.
Cross-layer transcoders (CLTs) enable circuit tracing that can extract high-level mechanistic explanations for arbitrary prompts and are emerging as general-purpose infrastructure for mechanistic interpretability. Because these tools operate at a relatively low level, their outputs are often treated as reliable descriptions of what a model is doing, not just predictive approximations. We therefore ask: when are CLT-derived circuits faithful to the model’s true internal computation?
In a Boolean toy model with known ground truth, we show a specific unfaithfulness mode: CLTs can rewrite deep multi-hop circuits into sums... (read 5126 more words →)
TLDR: recently, we wrote a paper proposing several evaluations of SAEs against "ground-truth" features computed w/ supervision for a given task (in our case, IOI [1]). However, we didn't optimize the SAEs much for performance in our tests. After putting the paper on arxiv, Alex carried out a more exhaustive search for SAEs that do well on our test for controlling (a.k.a. steering) model output with SAE features. The results show that:
Calculating l, the maximal number of simultaneously active features, yields strange results. For example, if we have 100 features and 100 neurons, l has to be < 100/(8 * ln(100)) = 2.7. But I would expect that 100 features can be simultaneously active because we have 100 dimensions, so the features can be orthogonal and independent. Am I understanding something wrong?
Produced as part of the SERI ML Alignment Theory Scholars Program - Summer 2023 Cohort
We would like to thank Atticus Geiger for his valuable feedback and in-depth discussions throughout this project.
Activation patching is a common method for finding model components (attention heads, MLP layers, …) relevant to a given task. However, features rarely occupy entire components: instead, we expect them to form non-basis-aligned subspaces of these components.
We show that the obvious generalization of activation patching to subspaces is prone to a kind of interpretability illusion. Specifically, it is possible for a 1-dimensional subspace patch in the IOI task to significantly affect predicted probabilities by activating a normally dormant pathway outside the IOI circuit. At the same time, activation patching the entire MLP layer where this subspace lies has no such effect. We call this an "MLP-In-The-Middle" illusion.
We show a simple mathematical model of how this situation may arise more generally, and a priori / heuristic arguments for why it may be common in real-world LLMs.
The linear representation hypothesis suggests that language models represent concepts as meaningful directions (or subspaces, for non-binary features) in the much larger space of possible activations. A central goal of mechanistic interpretability is to discover these subspaces and map them to interpretable variables, as they form the “units” of model computation.
However, the residual stream activations (and maybe even the neuron activations!) mostly don’t have a privileged basis. This means that many meaningful subspaces won’t be basis-aligned; rather than iterating over possible neurons and sets of neurons, we need to consider arbitrary subspaces of activations. This is a much larger search space! How can we navigate it?
A natural approach to check “how well” a subspace represents a concept is to use a subspace analogue of the activation patching technique. You run the model on input A, but with the activation along the subspace taken from an input B that differs from A only in the value of the concept in question. If the subspace encodes the information used by the model to distinguish B from A, we expect to see a corresponding change in model behavior (compared to just running on A).
Surpri...
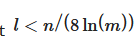
Thanks for your comment, I really appreciate it!
(a) I claim we cannot construct a faithful one-layer CLT because the real circuit contains two separate steps! What we can do (and we kinda did) is to have a one-layer CLT to have perfect reconstruction always and everywhere. But the point of a CLT is NOT to have perfect reconstruction - it's to teach us how the original model solved the task.
(b) I think that's the point of our post! That CLTs miss middle-layer features. And that this is not a one-off error but that the sparsity loss function incentivizes solutions that miss middle-layer features. We are working on adding more case studies to make this claim more robust.