Are you sure the "arrow forgetting" operation is correct? You say there should be an arrow when
for all probability distributions P over the elements of Ni, the approximation of Nj over P is no worse than the approximation of Ni over P
wherein [Ni]=[A→B←C] here, and [Nj]=[A−B−C]. If we take a distribution in which A⊥/C|B , then Nj is actually a worse approximation, because A⊥C|B must hold in any distribution which can be expressed by a graph in [Nj] ... (read more)
Thanks for the feedback. There's a condition which I assumed when writing this which I have realized is much stronger than I originally thought, and I think I should've devoted more time to thinking about its implications.
When I mentioned "no information being lost", what I meant is that in the interaction A→B, each value b∈B (where B is the domain of PB) corresponds to only one value of a∈A. In terms of FFS, this means that each variable must be the maximally fine partition of the base set which is possible with that variable's set of factors.
Under these conditions, I am pretty sure that A⊥C⟹A⊥C|B
I am confused about the last correspondence between Venn Diagram and BN equivalence class (this one: ). The graph X-Z-Y implies that X⊥Y|Z. Could you explain how the Venn diagram encodes this independence/orthogonality?
I used to think that starting new AI safety orgs is not useful because scaling up existing orgs is better:
they already have all the management and operations structure set up, so there is less overhead than starting a new org
working together with more people allows for more collaboration
And yet, existing org do not just hire more people. After talking to a few people from AIS orgs, I think the main reason is that scaling is a lot harder than I would intuitively think.
larger orgs are harder to manage, and scaling up does not
I made a deck of Anki cards for this post - I think it is probably quite helpful for anyone who wants to deeply understand QACI. (Someone even told me they found the Anki cards easier to understand than the post itself)
You can have a look at the cards here, and if you want to study them, you can download the deck here.
Possibly! Extending factored sets to continuous variables is an active area of research.
Scott Garrabrant has found 3 different ways to extend the orthogonality and time definitions to infinite sets, and it is not clear which one captures most of what we want to talk about.
I suspect that the fundamental theorem can be extended to finite-dimensional factored sets (i.e., factored sets where |B| is finite), but it can not be extended to arbitrary-dimension factored sets
If his suspicion is right, that means... (read more)
Finite Factored Sets are re-framing of causality: They take us away from causal graphs and use a structure based on set partitions instead. Finite Factored Sets in Pictures summarizes and explains how that works. The language of finite factored sets seems useful to talk about and re-frame fundamental alignment concepts like embedded agents and decision theory.
I'm not completely happy with
Finite factored sets are a new way of representing causality that seems to be more capable than Pearlian causality, the state
The summary has been updated to yours for both the public newsletter and this LW linkpost. And yes, they seem exciting. Connecting FFS to interpretability was a way to contextualize it in this case, until you would provide more thoughts on the use case (given your last paragraph in the post). Thank you for writing, always appreciate the feedback!
Consider the graph Y<-X->Z. If I set Y:=X and Z:=X
I would say then the graph is reduced to the graph with just one node, namely X. And faithfulness is not violated because we wouldn't expect X⊥X|X to hold.
In contrast, the graph X-> Y <- Z does not reduce straightforwardly even though Y is deterministic given X and Z, because there are no two variables which are information equivalent.
I'm not completely sure though if it reduces in a different way, because Y and {X, Z} are information equivalent (just like X and {Y,Z}, as well as Z and {X,... (read more)
Finally got around to looking at this. I didn't read the paper carefully, so I may have missed something, but I could not find anything that makes me more at ease with this conclusion.
Ben has already shown that it is perfectly possible that Y causes X. If this is somehow less likely that X causes Y, this is exactly what needs to be made precise. If faithfulness is the assumption that makes this work, then we need to show that faithfulness is a reasonable assumption in this example. It seems that this work has not been done?
If we can find the precise and reasonable assumptions that exclude that Y causes X, that would be super interesting.
Would it be possible to formalize "set of probability distributions in which Y causes X is a null set, i.e. it has measure zero."?
We are looking at the space of conditional probability table (CPT) parametrizations in which the indepencies of our given joint probability distribution (JPD) hold.
If Y causes X, the independencies of our JPD only hold for a specific combination of conditional probabilities. Namely those in which P(X,Z) = P(X)P(Z). The set of CPT parametrizations with P(X,Z) = P(X)P(Z) has measure zero (it is lower-dimensional than the spa... (read more)
I'm pretty sure that you can prove that finite factored sets have this property directly, actually!
2Frederik Hytting Jørgensen
For example, in theorem 3.2 in Causation, Prediction, and Search, we have a result that says that faithfulness holds with probability 1 if we have a linear model with coefficients drawn randomly from distributions with positive densities.
It is not clear to me why we should expect faithfulness to hold in a situation like this, where Z is constructed from other variables with a particular purpose in mind.
Consider the graph Y<-X->Z. If I set Y:=X and Z:=X, we have that X⊥Y|Z, violating faithfulness. How are you sure that you don't violate faithfulness by constructing Z?
This is a very good point, and you are right - Y causes X here, and we still get the stated distribution. The reason that we rule this case out is that the set of probability distributions in which Y causes X is a null set, i.e. it has measure zero.
If we assume the graph Y->X, and generate the data by choosing Y first and then X, like you did in your code - then it depends on the exact values of P(X|Y) whether X⊥Z holds. If the values of P(X|Y) change just slightly, then X⊥Z won't hold anymore. So given that our graph is Y->X, it's really unlikely (I... (read more)
I'm not quite convinced by this response. Would it be possible to formalize "set of probability distributions in which Y causes X is a null set, i.e. it has measure zero."?
It is true that if the graph was (Y->X, X->Z, Y->Z), then we would violate faithfulness. There are results that show that under some assumptions, faithfulness is only violated with probability 0. But those assumptions do not seem to hold in this example.
Thank you very much. That explains a lot. To repeat in my own words for my understanding: In my example perturbing any of the probabilities, even slightly, would upset the independence of Z and X. So in some sense their independence is a fine tuned coincidence, engineered by the choice of values. The model assumes that when independences are seen they are not coincidences in this way, but arise from the causal structure itself. And this assumption leads to the conclusion that X comes before Y.
I agree that 1. is unjustified (and would cause lots of problems for graphical causal models if it was).
Interesting, why is that? For any of the outcomes (i.e. 00, 01, 10, and 11), P(W|X,Y) is either 0 or 1 for any variable W that we can observe. So W is deterministic given X and Y for our purposes, right?
If not, do you have an example for a variable W where that's not the case?
I think W does not have to be a variable which we can observe, i.e. it is not necessarily the case that we can deterministically infer the value of W from the values of X and Y. For example, let's say the two binary variables we observe are X=[whether smoke is coming out of the kitchen window of a given house] and Y=[whether screams are emanating from the house]. We'd intuitively want to consider a causal model where W=[whether the house is on fire] is causing both, but in a way that makes all triples of variable values have nonzero probability (which is true for these variables in practice). This is impossible if we require W to be deterministic once (X,Y) is known.
Further, I’m pretty sure the result is not “X has to cause Y” but “this distribution has measure 0 WRT lebesgue in models where X does not cause Y”
Yes that's true. Going from "The distributions in which X does not cause Y have measure zero" to "X causes Y" is I think common and seems intuitively valid to me. For example the soundness and completeness of d-separation also only holds but for a set of distributions of measure zero.
I think this could be right, but I also think this attitude is a bit too careless. Conditional independence in the first place has lebesgue measure 0. I have some sympathy for considering something along the lines of "when your posterior concentrates on conditional independence, the causal relationships are the ones that don't concentrate on a priori measure 0 sets" as a definition of causal direction - maybe this is implied by the finite factored set definition if you supply an additional rule for determining priors, I'm not sure.
Also, this is totally not the Pearlian definition! I made it up.
Are you sure the "arrow forgetting" operation is correct?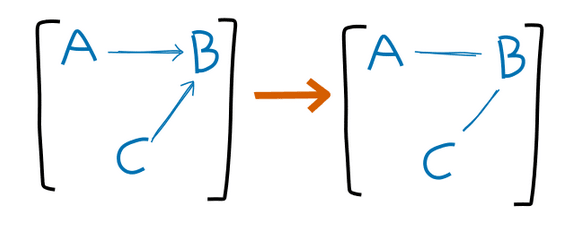
You say there should be an arrow when
wherein [Ni]=[A→B←C] here, and [Nj]=[A−B−C]. If we take a distribution in which A⊥/C|B , then Nj is actually a worse approximation, because A⊥C|B must hold in any distribution which can be expressed by a graph in [Nj] ... (read more)