FWIW - here (finally) is the related post I mentioned, which motivated this observation: Natural Abstraction: Convergent Preferences Over Information Structures The context is a power-seeking-style analysis of the naturality of abstractions, where I was determined to have transitive preferences.
It had quite a bit of scope creep already, so I ended up not including a general treatment of the (transitive) 'sum over orbits' version of retargetability (and some parts I considered only optimality - sorry! still think it makes sense to start there first and then...
Not sure this is exactly what you meant by the full preference ordering, but might be of interest: I give the preorder of universally-shared-preferences between "models" here (in section 4).
Basically, it is the Blackwell order, if you extend the Blackwell setting to include a system.
Thanks for the reply. I'll clean this up into a standalone post and/or cover this in a related larger post I'm working on, depending on how some details turn out.
What are here?
Variables I forgot to rename, when I changed how I was labelling the arguments of in my example. This should be , , retargetable (as arguments to ).
I appreciate this generalization of the results - I think it's a good step towards showing the underlying structure involved here.
One point I want to comment on is transitivity of , as a relation on induced functions . Namely, it isn't, and can even contain cycles of non-equivalent elements. (This came up when I was trying to apply a version of these results, and hoping that would be the preference relation I was looking for out of the box.) Quite possibly you noticed this since you give 'limited transitivity' in Lemma B.1 rather than fu...
I think this line of research is interesting. I really like the core concept of abstraction as summarizing the information that's relevant 'far away'.
A few thoughts:
- For a common human abstraction to be mostly recoverable as a 'natural' abstraction, it must depend mostly on the thing it is trying to abstract, and not e.g. evolutionary or cultural history, or biological implementation. This seems more plausible for 'trees' than it does for 'justice'. There may be natural game-theoretic abstractions related to justice, but I'd expect human concepts and beha...
A while back I was looking for toy examples of environments with different amounts of 'naturalness' to their abstractions, and along the way noticed a connection between this version of Gooder Regulator and the Blackwell order.
Inspired by this, I expanded on this perspective of preferences-over-models / abstraction a fair bit here.
It includes among other things:
- the full preorder of preferences-shared-by-all-agents over maps X→M(vs. just the maximum)
- an argument that actually we want to generalize to this diagram instead[1] :
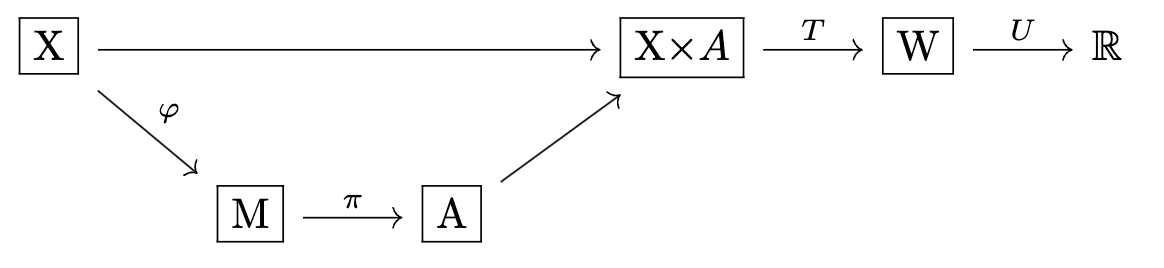
- an extension to preferences
... (read more)