Geometry of vectors: direction
To understand geometry of vectors, we need a good way to compare directions, and a way to rotate vectors. It was hard to find a good way to algebraically represent differences between directions, and rotations. Lots of cumbersome and complicated formulas and methods were developed – which you may have suffered through in a high-school trigonometry class – before we finally found a clean and powerful way of thinking about it, that is also much more intuitive!
This article is a quick introduction to the important concepts and ideas for handling vector directions, with lots of visual representations of them. This will help us understand the pieces that go into the geometric product, which is a powerful way to manipulate these concepts algebraically. In turn, having the geometric product at hand will allow us to gain a more substantial understanding of the ideas introduced here. [1]
Comparing direction
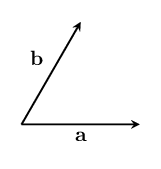
What would it take to change the direction of to match the direction of ? We want our answer to be specific enough that we could use it to tell our friend exactly how to make the same change in direction.
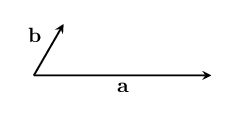
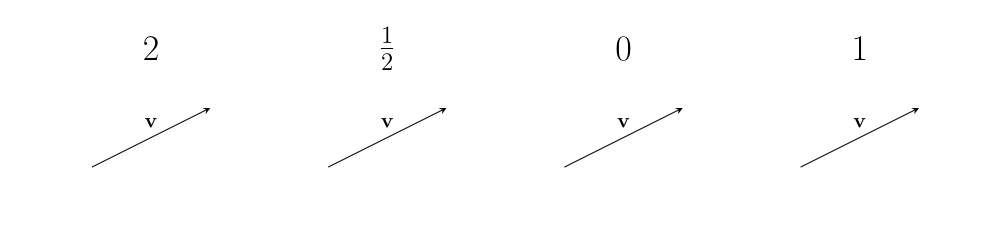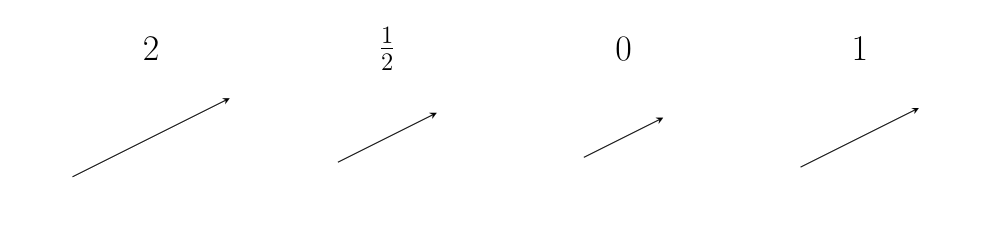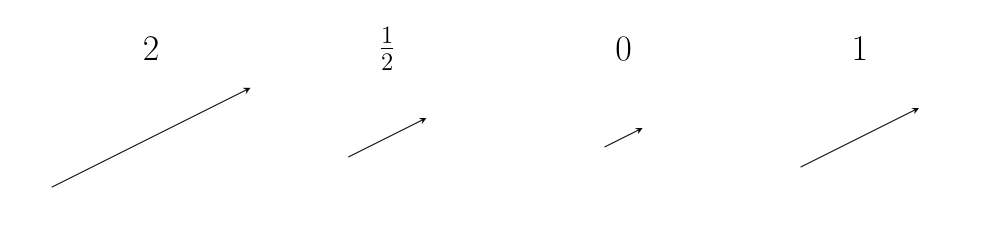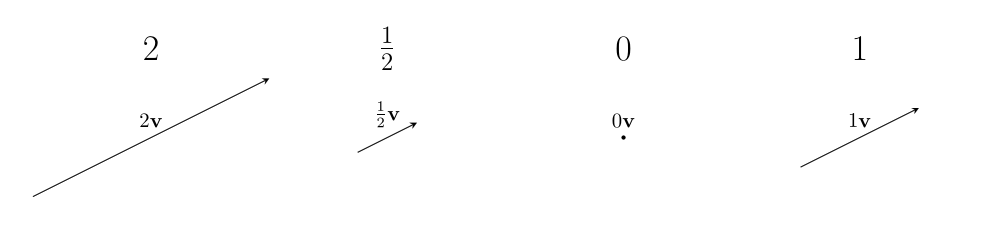
It should not depend on the size of the vectors:
It should also be the same for vectors which have been rotated in the same direction:
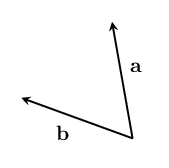
And it should be able to work for vectors in three (or more) dimensions. So you should be able to tell your friend whether you want to change the direction of to match , or to match :
Try thinking of a way to do this yourself before moving on.
Angle?
An angle is a good way to describe the size of the difference between the directions of the two vectors, but by itself it is missing information about which way you would need to turn it to get the vectors to match. In two dimensions you can get away with using negative angles to represent this, but in three (or more) dimensions, it becomes clear that an angle by itself will not work.
Show solution
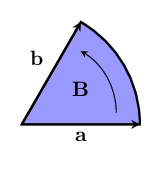
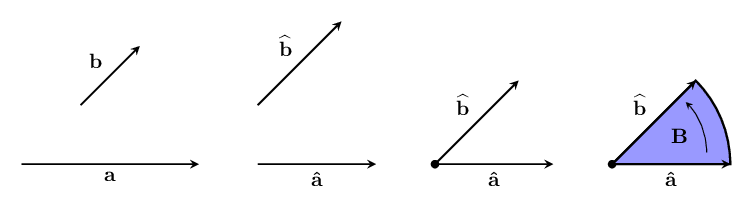
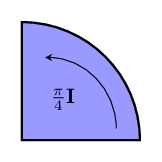
We need to keep track of three things: the size of the turn we would need, the plane in which the turn takes place, and which way to turn it within the plane. Sound familiar? Considering the plane together with the direction of the turn in the plane as a 2-dimensional direction, we can make a vector! Shown below is a bivector that can represent the difference in direction from to :
However, this is a different kind of vector from our vectors and , so to keep things from getting confusing, we will call the new kind of vector a bivector.
And since bivectors are a kind of vector, we can describe a bivector exactly by describing it in terms of a basis for bivector space! We'll see how all of this works below.
Bivectors
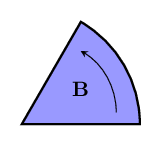
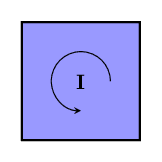
So how do bivectors work? A bivector is a new type of vector. Its size is its area, and its direction is a two-dimensional sort of direction that determines its orientation in space, along with which way it turns things.
The bivector lies in the plane of your screen, and has a counter-clockwise orientation (i.e. it moves things in the opposite way that the hands of a clock move). We usually use a bold, upper-case letter for bivectors.
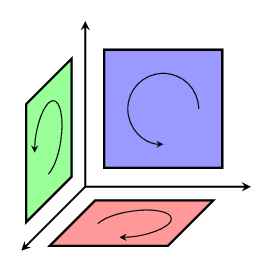
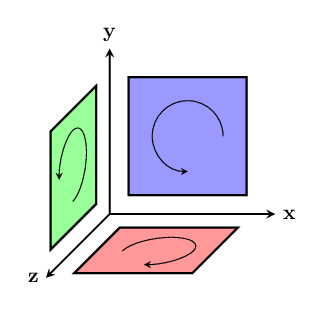
Bivectors are particularly important in three-dimensions, where there are many more directions that they could have:
The size of a bivector is its area, so the unit bivector has the area of a square with unit length sides:
We'll usually use to write a unit bivector.
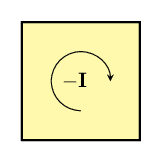
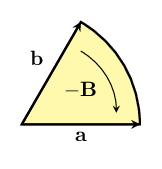
The negative of a bivector is a bivector with the same size and which lies in the same plane, but which turns things the opposite way. You can think of it like flipping a piece of paper over:
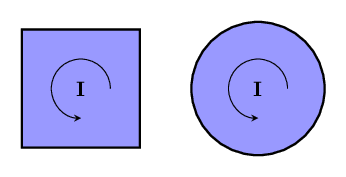
As with all types of vectors, the size and direction of a bivector are all there is to it! This means that bivectors do not have positions or shapes, since we do not keep track of that information anywhere. So since these bivectors have the same direction, and both have area 1, these are both the same bivector:
Similarly, rotating a bivector without changing the plane it lies in doesn't change it since its size and direction remain the same. So this bivector stays the same even though we're shaking it around:
We can add two bivectors to get another bivector. This is one place where doing things algebraically helps us a lot – it is kinda hard to visualize what the new bivector will look like. Here is one way to do it:
When two bivectors have the same (or opposite) direction though, it's a lot easier: addition can be done just by adding (or subtracting) the sizes of the two bivectors:
Bivector basis
If we have a basis of ordinary vectors, we can use these to create a basis for the bivectors that would be needed for vectors in that space. For any pair of basis vectors, we can use the bivector that describes the difference in direction of those two vectors.
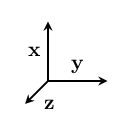
In three dimensions, there are three possible pairs: xy, yz, and xz. Here's the normalized basis we can construct from these pairs:
In two dimensions, there is only one pair, and the space of bivectors is one-dimensional:
How many dimensions does bivector space have for for vectors in 4-dimensions?
Answer
It has 6-dimensions. If the basis for ordinary vectors in 4-dimensions is , , , , then the basis for the bivectors will be the bivectors for each of the pairs: , , , , , and .
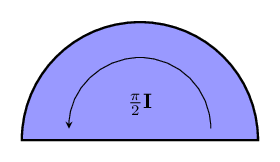
Now that we know about bivectors, lets go back to seeing how we can use them to describe differences in direction. We can visualize the difference in direction between two vectors and by normalizing them, adding them both to the same point, and then using the area swept out by rotating one to match the other one. This area is what we'll use for the size of the bivector that represents the difference between these two directions.
We'll use the direction of a bivector for the direction we w
The unit circle has area (about ):
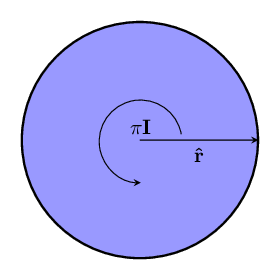
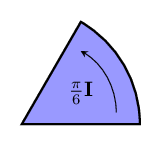
We use the sizes of bivectors to describe how much of a rotation is needed. The most natural value to use is just the area of the piece of the unit circle we saw from before. Then we can use fractions of to say what fraction of a full turn is needed. [2]
A special amount of direction change is given by a bivector of size . Equally far from both vector and its reverse - in the most completely different direction. There are lots of words for vectors that differ by this bivector: we can say that the vectors are at right angles to each other, perpendicular, or orthogonal.
Rotating vectors
When applied to vectors, scalars represent different actions we can do to a vector: the act of stretching a vector, or shrinking one, or reversing one, or erasing one, or leaving it alone.
Rotation is another action we can apply to vectors. Things that rotate other things are called rotors:
We usually will use a capital to write a rotor. Since bivectors can describe differences in direction, we can also use them to describe rotors. To make a rotor from the bivector , we use the letter , like this: . [3]
!rotor action examples using exponential rotation (gifs)
The reason we don't use a bivector directly is that the rules for combining rotors are different from the rules for combining bivectors (which are just the vector arithmetic rules). It can't be bivector addition, since rotors are non-commutative:
And it can't be direct multiplication, because if we have two rotors in the same plane, the size of the bivector for the combined rotor should be the sum of the sizes of the bivectors for the two rotors, and not the product. As an extreme case, the rotor with the zero bivector just leaves things the same, instead of erasing them.
In algebra, scalars act on vectors through ordinary multiplication. For example, we can double a vector , by multiplying it by 2: to get . We would like to have an algebraic way to depict how rotor actions work
In order to depict how rotor actions work algebraically, we'll first need to develop the geometric product. In fact, getting rotors to work algebraically is an important part of what led to the development of the geometric product in the first place!
We're really close to having a basic grasp of all the ideas that go into the geometric product! We've learned in this page about the geometry of vector directions; the last thing we'll need is a geometric understanding of how the sizes of different vectors relate to each other.
Once we have the geometric product, we'll be able to take a deeper look at how rotors work.
- ^︎
Note that we are not using angles in this page, which is the typical way of thinking about the directions of vectors. Instead, we are using a closely related, but different, concept called a bivector. Bivectors allow us to see deeper facts about rotations more easily than angles will, and when the time is right, we will see exactly how angles fit in with the concepts presented here.
- ^︎
But isn't this half of what it should actually be?!? Well, it's true that the equivalent angle has a value (in radians) equal to twice the area of the bivector. While radians measure the length of the arc swept out, bivectors measure the area swept out – so rest assured that this is actually the right way to do it.
- ^︎
If you are familiar with exponents, you might notice that this is the same as exponential notation. We'll later see that there is a deep connection between rotors and exponents, which is the reason we use this notation!