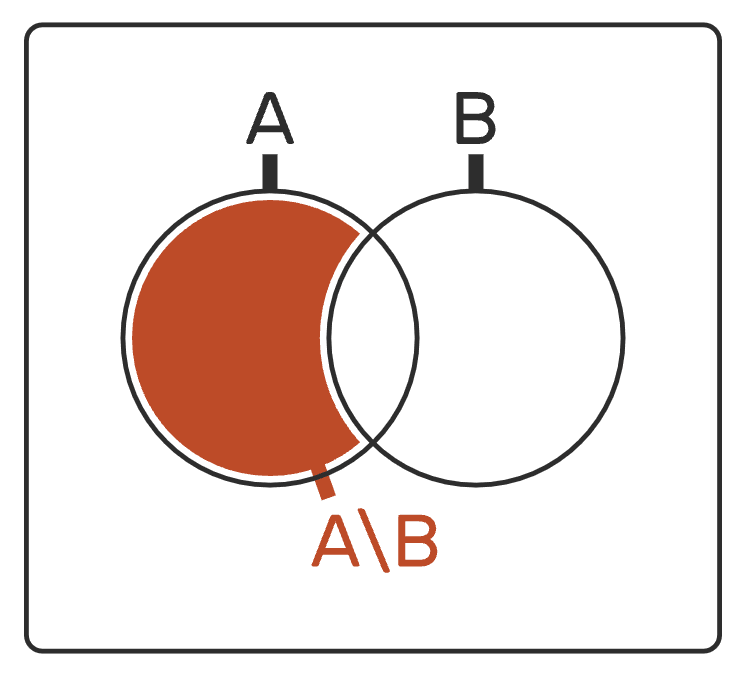
The relative complement of two sets and , denoted , is the set of elements that are in while not in .
Formally stated, where
That is, Iff is in the relative complement , then is in and x is not in .
For example,
If we name the set as the set of all things, then we can define the Absolute complement of the set , , as
Parents: