Cross-posted from Telescopic Turnip
Disclaimer: This article is about living organisms, and how they are sculpted by evolution. Any use of mathematics is metaphorical, not literal – it's only there to give a sense of scale. Apologies to all the people who got correctly offended by my shamelessly hand-wavy references to Kolmogorov complexity.
As we all know, humans are terrible at building butterflies. We can make a lot of objectively cool things like nuclear reactors and microchips, but we still can't create a proper artificial insect that flies, feeds, and lays eggs that turn into more butterflies. That seems like evidence that butterflies are incredibly complex machines – certainly more complex than a nuclear power facility.
Likewise, when you google "most complex object in the universe", the first result is usually not something invented by humans – rather, what people find the most impressive seems to be "the human brain".
As we are getting closer to building super-human AIs, people wonder what kind of unspeakable super-human inventions these machines will come up with. And, most of the time, the most terrifying technology people can think of is along the lines of "self-replicating autonomous nano-robots" – in other words, bacteria.
Humans are just very humbled by the Natural World, and we are happy to admit that our lame attempts at making technology are nothing compared to the Complexity of Life. That's fair enough – to this day, natural living organisms remain the #1 collection of non-human technology we get to observe and study. What makes these organisms so different from human-made technology?
Here is my thesis: the real reason why humans cannot build a fully-functional butterfly is not because butterflies are too complex. Instead, it's because butterflies are too simple.
As I'll argue, humans routinely design systems much more complex than butterflies, bacteria or brains – and if you look at all the objects in the room, your brain is probably not even in the top 5.
As it turns out, there are some pretty hard fundamental limits on the complexity of living organisms, which are direct consequences of the nature of evolution.
But before going into that, let's examine how complex living organisms like you and me really are.
You are simpler than Microsoft Word™
By "complexity", I mean complexity in the Kolmogorov sense: how much information you need to completely describe something. This definition is particularly convenient for two things: software, and living organisms.
For example, the Tetris game fits in a 6.5 kB file, so the Kolmogorov complexity of Tetris is at most 6.5 kB. It's a pretty simple system. In contrast, the complete Microsoft Word™ software is a much more complicated object, as takes 2.1 GB to store.
We can do the same with living organisms. The human genome contains about 6.2 billion nucleotides. Since there are 4 nucleotides (A, T, G, C), we need two bits for each of them, and since there are 8 bits in a byte, that gives us around 1.55 GB of data.
In other words, all the information that controls the shape of your face, your bones, your organs and every single enzyme inside them – all of that takes less storage space than Microsoft Word™.
We can go further: only 10% of the human genome is actually useful, in the sense that it's maintained by natural selection. The remaining 90% just seems to be randomly drifting with no noticeable consequences. That brings your complexity down to 155 MB – not even a CD-ROM worth of data.
(There's an open debate about whether genomes really contain all information needed to describe a species – since each cell is built from another cell, there might be additional information in physical cell structures. My guess is that, since this non-DNA information is not a substrate of evolution the way DNA is, it likely doesn't contribute significantly to overall complexity.)
I like the organism/software comparison, because it goes to show how insanely compressed living organisms are compared to human-made software. Notice the log scale:
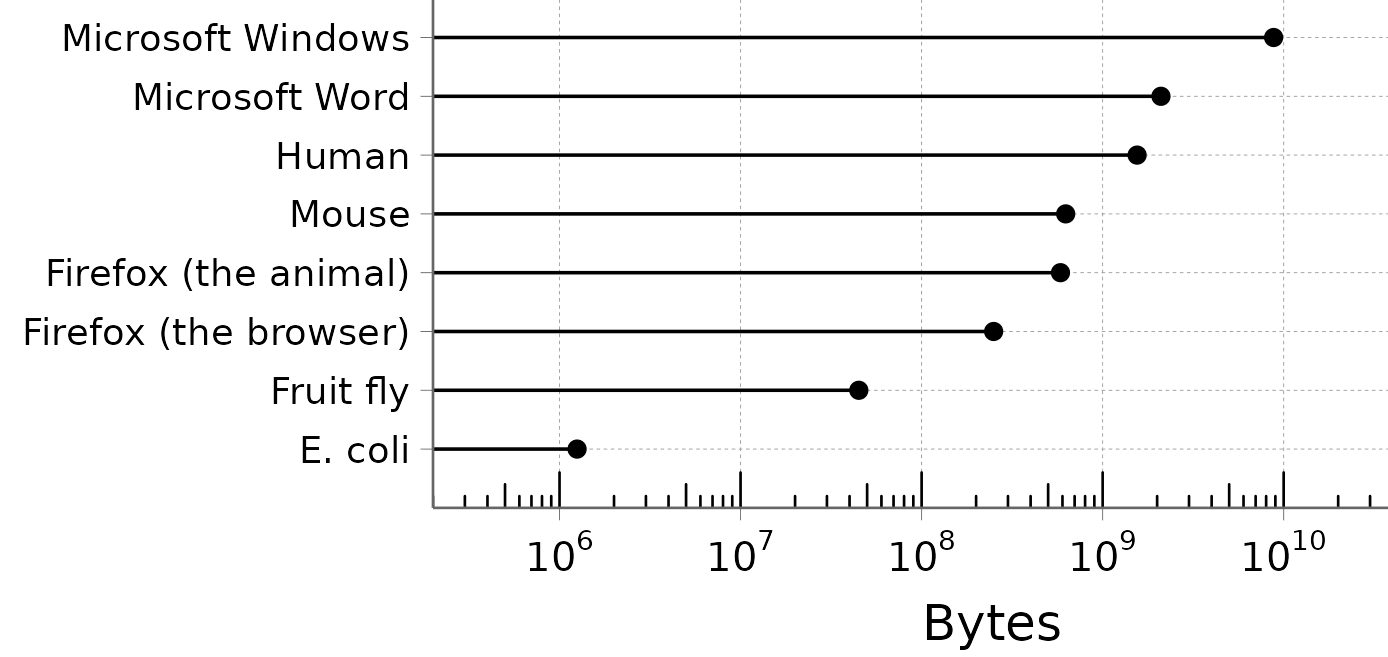
Take a moment to appreciate how simple bacteria are. Escherichia coli has a genome of about 5 million nucleotides, i.e. 1.25 MB. That is small enough to fit on a 1.44 MB floppy disk.[1]
In this case, being simple is very different from being capable – we are still talking about self-replicating micro-robots. E. coli can deploy a little motor to swim in the direction of nutrients, it has little retractile arms, a self-repairing envelope, a 5-years battery life, complicated collective tactics, and an immune system so clever that when we discovered it, it was a huge leap forward for human technology. All of that is encoded in a genome 1/1000 the size of Microsoft Word.
(To be fair, not all bacteria fit on a floppy disk. For example, Myxococcus xanthus, with its 2.5 MB genome, is too large. You will have to invest in more advanced storage technologies, like the 40-MB Iomega® 1999 Clik™ PocketZip.)
(That said, M. xanthus is a predatory bacterium famous for its ability to eavesdrop on the chemical messages of its preys, so it's basically malware. You don't want that on your floppy disk anyway.)
I think this dazzling level of compression is what really distinguishes natural, evolution-selected designs from human-made technology.
For example, your body contains a nice little structure called the nephron. It's your kidney's basic filtration device – it gets rid of harmful waste molecules while keeping the precious stuff your body wants to keep.
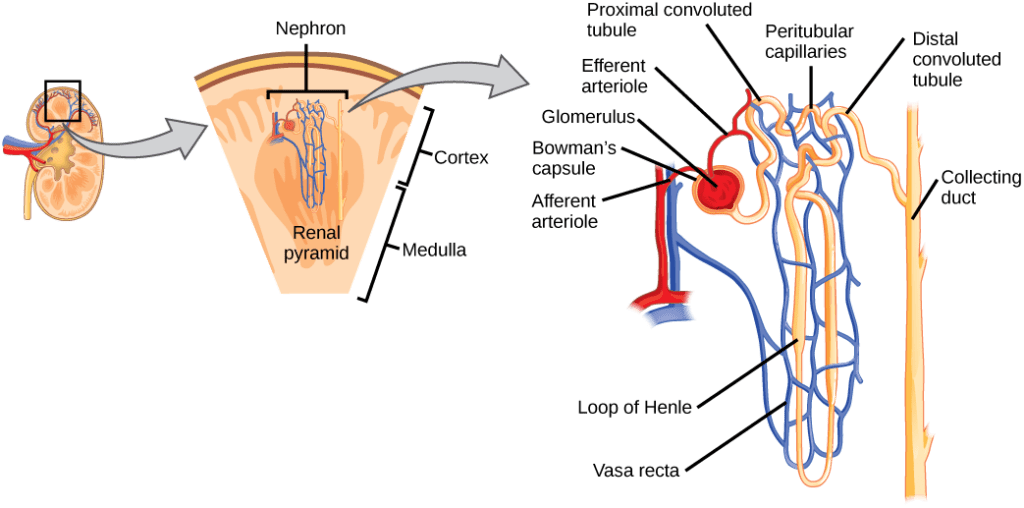
Sure, this looks pretty complex, but it's not far more complex than the kind of facilities humans use to treat wastewater. In fact, human engineers are totally capable of building an artificial kidney that works just fine.
What makes something like the nephron impressive is not the super-human complexity of its workings. What's impressive is that you have one million copies of the nephron in each of your kidneys, and the entire thing spontaneously assembles starting from a single cell, and all of this is encoded in a genome that only contains 150 MB of information. That's not even 1/4 of a CD-ROM. Could the complete specification of a water treatment facility fit on a CD-ROM? I don't think the regulatory documents alone would fit.
This level of simplicity is beyond anything humans have ever created. This is what I mean by "mechanisms too simple for humans to design".
Of course, this level of compression completely changes the design rules. To be competitive on the fitness market, living organisms need to come up with clever ways to do very complicated operations with a very small number of components. And, as we'll see, they are super-humanely good at it.
But why are living organisms so simple in the first place?
Blood for the Information Theory God
Evolution works by alternating between mutation and natural selection. How does that affect the information content of a genome? To put it in a super-hand-wavy way:
- Mutations degrade information. One nucleotide encodes 2 bits of information, so a random mutation introduces 2 bits of uncertainty.
- Natural selection accumulates information. If you start from a mix of all possible sequences, and only the fittest fraction P of the population survives, you gain -log(P) bits of information. Notice that if you have an even mix of A, T, G and C at a given position, picking the "fittest" nucleotide is equivalent to picking the top 25% of the population, so the information gain is -log(0.25) = 2 bits of information, which is indeed the information content of one nucleotide.
I mean this merely as an intuition pump, but you can put this in more precise mathematical terms. Therefore, maintaining a functional genome is a perpetual burden: with each generation, as our imperfect DNA-polymerase introduces new random mutations, some of the information content of our genomes is lost. To keep the species going, this lost information has to be gained back through natural selection.
This comes with a huge cost: the only way to accumulate more information would be to have more "efficient" selection – that is, a larger fraction of the population must die without offspring in each generation. The Information Theory God wants blood.
To get a sense of what this means in practice, let's do a thought experiment.
Imagine the X social network, but with a little modification: tweets are generated by natural selection. In this version, you cannot write new tweets – instead, whenever someone pushes the "retweet" button, it is replicated imperfectly and a few characters might be changed at random.
With every retweet, there is a small chance that the changes will make the tweet slightly better. A better tweet is more likely to be retweeted, and the process repeats until the tweet evolves into the most viral, unstoppable incendiary hot take ever.[2]
But, realistically, it is vastly more likely that introducing a random change into a tweet will just introduce a nonsense typo, making it less good than the original.
And that's enough to put a hard limit on the length of a tweet. To see why, let's consider two equally-good tweets, both good enough to be retweeted 10 times on average, with a mutation rate of 1% per character.
- Tweet 1 is 280-characters long. Then 94% of the retweets have a mutation somewhere, and only 6% are identical to the original. So, most of the time, all of the tweet's progeny will have one or more random letter substitution, and that's almost always a bad thing. The tweet's offspring is becoming less dank with each generation and its cursed dynasty quickly vanishes into darkness.
- Tweet 2 is 140-characters long. Now the fraction of mutants is only about 75%. This means that, every generation, you will get 2 or 3 copies of the original tweet among the offspring. If each of them gets retweeted 10 more times, you now have a self-sustaining population.
Sure, it is possible that one of the mutants of the 280-characters long Tweet 1 will be extraordinarily dank by sheer luck, but it will get very few opportunities to find such a good mutation before the lineage goes extinct. Meanwhile, the shorter Tweet 2 gets a potentially unlimited number of attempts, so it has a decent shot at finding a beneficial mutation eventually.
So we have a trade-off between a few parameters:
- The retweet rate, T, a.k.a "fitness"
- The mutation probability per character, μ
- The length of the tweet, L
As the tweet is retweeted T times, the expected number of identical copies among the offspring is
This represents the number of unmutated copies of the tweet you propagate - basically backup copies of the original. For the tweet to sustainably replicate and evolve while preserving its information, this number should be at least 1. So the length of the tweet is limited to:
And here we are: there's a hard limit on how much information you can fit in a tweet.
Of course, this Twitter parable is very different from real-life DNA information, but the general idea is the same (and biologists have come up with all kinds of dirty ghetto mathematical approximations to formalize it). No matter how you put it, the inescapable part is how the fraction of retweets without mutations decreases exponentially with L: to make the tweet twice as long, the number of retweets would have to be squared.
This is why you shouldn't see evolution as a "random walk" through the space of possible genomes. Instead, most of the work of natural selection is simply to purge the bad mutants and maintain a core functional population. It's only on top of that, when the population manages to perpetuate over many generations, that evolution gets to tinker a little bit and try to come up with improvements.
In practice, information accumulates pretty slowly – in a paper from the 1960s, Motoo Kimura estimated that we've gained about 0.2 bits of information per year since the Cambrian.
The Barrier
What about the mutation rate μ? Can't we make an organism arbitrarily complex by decreasing the mutation rate? After all, it’s not like there is a mathematical limit to the accuracy of DNA replication machinery, right?
Well, there is, in fact, a mathematical limit to the accuracy of DNA replication machinery.
It's not that better polymerases don't exist. It's that evolution is not precise enough to discover them. The reason for that is called the Drift Barrier – a direct consequence of genetic drift, the change in allele frequencies due to the random happenstance of life.
The intensity of genetic drift scales with 1/N, with N the population size. (To get an intuition why, imagine a winner-take-all scenario where you start with N individuals. Each of these N initial individuals has a 1/N probability of being the winner, just by chance, so a neutral mutation must also have a 1/N probability of being accidentally selected.) This is essentially the "resolution limit" of evolution. If the relative improvement that comes with a mutation is smaller than 1/N, then it will be drowned in randomness and natural selection can't reliably select for it.
Now, reducing the mutation rate has diminishing returns. Even in conditions where every single mutation is 100% deadly (so there is maximal selection pressure for lower mutation rates), reducing the number of mutations per generation from 10% to 1% saves 9% of the offspring, but going from 1% to 0.1% only saves 0.9%, and so on. Eventually, the effect becomes so small that it hits the 1/N Drift Barrier. Then, evolution can't push it any further down.
And if you look across the tree of life, the mutation rate does indeed scale inversely with population size. This is a rare and precious case where people tried to describe biology with math, and it actually worked:
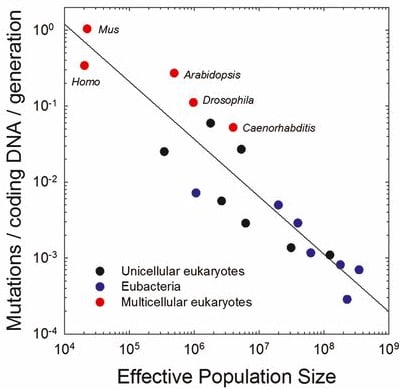
Of course, the largest, most complex organisms also tend to have the smallest populations, so there is no way out: complexity is limited by mutation rate, which is limited by population size, which is itself limited by complexity.
Needless to say, none of these limits apply to human inventions, which is why your phone's web browser can be orders of magnitude more complex than you are.
Implications for Pokémon (SPECULATIVE)
If a species isn't able to maintain the information content of its genome, this information evaporates. What does this look like in practice? There are various theoretical scenarios with cool names like error catastrophes, mutational meltdowns and extinction vortex to describe what happens.
To illustrate that point, let's contemplate the possibility of using genetic engineering to bring your favorite Pokémon to life.
Say you want to immanentize Pikachu. Using speculative advanced AI technology, you generate a complete genome that codes for a picture-perfect Pikachu. Then you synthesize it and you inject the embryos inside some suitable host.
Here's the crucial point: real-life animals represent special cases: their body plans arise from relatively simple rules that can be encoded in a genome small enough to be maintained, according to their population size. Encoding an animal into a genome is a vastly over-determined problem.
But the perfect Pikachu almost certainly isn't like that. There's no simple Pikachu-generating function. To get the shape and colors just right, you likely need to add numerous genetic circuits and morphogens to precisely adjust the position of each feature. And that requires endowing your Pikachus with a ridiculously long genome.
The problems begin when the first-gen Pikachus start to reproduce. Even if they start with almost-perfect DNA-polymerases, the Drift Barrier means that mutations in the polymerases themselves cannot be purged, so the mutation rate inevitably goes up. Since the Pikachu's genome is so humongous, there will be new mutations in all of the offspring, so there's nothing you can do to prevent them from accumulating malformations.
As the population declines, natural selection becomes less and less efficient, and everything gets worse and worse. In bad enough cases, the species can even spiral down to extinction, even in the absence of any competitor.
And you can't even breed them back into their original Pikachu shape, because once you've lost the information, the chances of the original alleles ever reoccurring in isolation are vanishingly small.
(The implications for catgirls are too sad to discuss.)
Seeing like a 1.25 MB genome
The information constraints are mostly relevant for large, complex, macroscopic animals with small population sizes.
But we could also go in the other direction. On the opposite side of the trade-off, you find bacteria, who decided instead to swarm the world with huge populations of absurdly simple creatures.
To highlight the deep divide between these two strategies, let's look at the genomes. Remember that the human genome contains 10% useful information, interspersed with 90% nonsensical wastelands. On the other hand, here is the genome of the gut bacterium Escherichia coli. The colorful blocks are things that code for content. Only the little spaces in between are non-coding, and most of that has some important regulatory effect:

The genomes of bacteria (and other prokaryotes) look like the walled city of Kowloon. In comparison, the genomes of animals (and other eukaryotes) look more like the steppes of Kazakhstan.
You might be wondering why life would diverge to these two antipodes. It's as if the two realms were being pulled apart by inescapable forces. That's because they are.
In fact, considering the information-theory arguments above, bacteria could afford to have much larger genomes without going into error catastrophes. They replicate themselves with insane accuracy – if a bacterium divides 1000 times, 999 of the daughters will be exactly identical to their mother – without a single mistake in any of the 15 million bases.
But there are other factors that drag down the size of bacterial genomes. I heard of three reasons:
- The membrane / cytoplasm ratio: In humans, the chemical reactions associated with respiration are done by mitochondria. But bacteria don't have those. Instead, respiration is done by enzymes inserted in the bacteria's membrane. Here's the problem: if you double the size of a cell, the volume is multiplied by 8, but the surface area is only multiplied by 4. So if you try to add more cool mechanisms inside a cell, you will soon run out of membrane real estate to generate the energy to power these mechanisms.
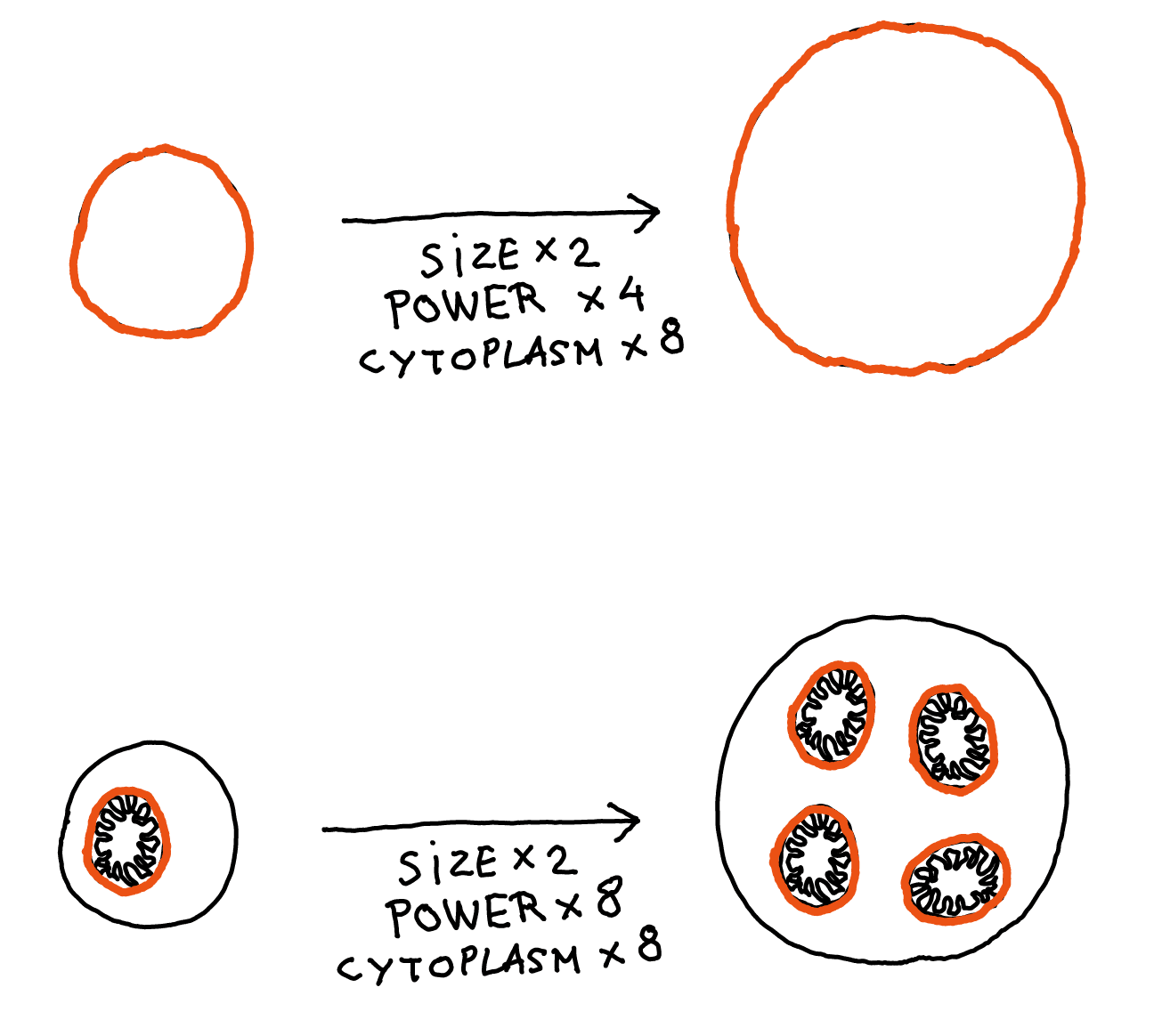
This is actually one of the main reasons mitochondria are so useful: they allow the amount of membrane (and therefore the energy-production capacity) to scale with volume like everything else, so it's no longer a limit to cell size.
- Bacteria's evolution is more precise: If you compare the cost of making a few hundred nucleotides of DNA to the total cost of making the whole cell, the former is a tiny fraction. But bacteria have huge populations, so the Drift Barrier is very small for them. If they can save a little bit of energy by removing 100 bp of useless DNA, evolution is precise enough to get rid of it.
But eukaryotes, with their huge genomes and small populations, can't see any difference. And so, the junk DNA just accumulates. - Bacteria just like to delete stuff: When bacteria mutate, even in the absence of selection, they are 10 times more likely to remove nucleotides than to insert them. The reasons why are still mysterious (eukaryotes don't do that), but the consequences are clear: any sequence in the genome that is not especially useful will just naturally shrink over time.
These are just mechanistic explanations. For a deeper look on the metaphysics of this, I recommend Aysja's piece on Seeds of Science, Why Are Bacteria So Simple.
Anyways, everything about bacteria seems to be optimized for minimalism, allowing for immense populations and rapid evolution. This is how you end up with self-replicating nanobots whose genomes fit on a floppy disk.
Mechanisms too simple for humans to design
With these constraints in mind, we can now fully appreciate the magnificent simplicity of natural mechanisms.
Here is one of my favorite examples. It's a really clever mechanism Bacillus subtilis uses to navigate the world.
Bacillus subtilis is a rod-shaped bacterium that lives buried in the soil, near the roots of plants. Here's what it looks like when it grows:

For soil bacteria, a typical day looks like: escape killer fungi, find delicious nutrients and, perhaps most importantly, find oxygen to breathe. How can such a small creature find the places where it can grow the fastest, and move towards them?
It's interesting to think about this problem from the point of view of a human engineer: if you wanted to make a tiny robot that moves in the direction that maximizes growth, how would you do that? What is the simplest solution you can find?
Here is a naive "human-style" solution: put some oxygen sensors everywhere on the surface of the cell, then somehow measure the difference between two opposite sides. If you detect a gradient, you activate a bunch of tiny propellers on the least oxygenated side, so the bacteria swim towards the oxygen. Repeat this for every possible nutrient.
This is costly, easy to break, and extremely hard to evolve. But I don't think I could come up with anything much better. (If you take time to think about this, feel free to pause reading and write your best solution in the comments!)
Now, here is what B. subtilis actually does. The strategy is a combination of two phenomena:
First, B. subtilis doesn't grow straight. It grows twisting, kind of like this:
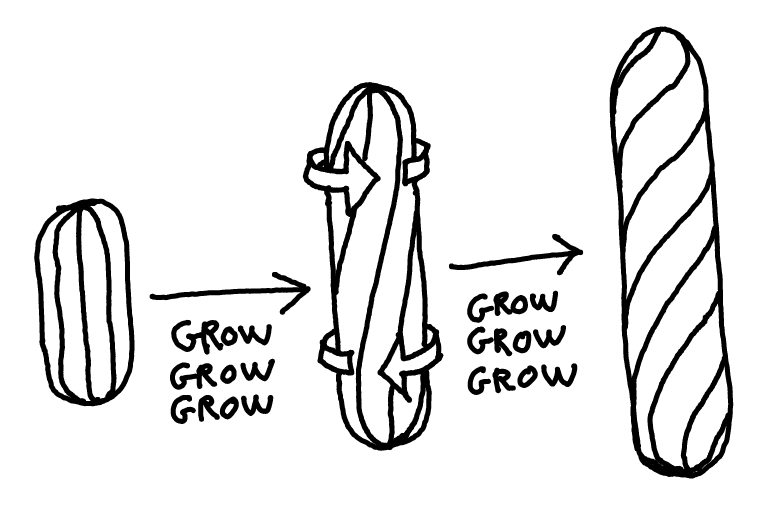
(If this is hard to visualize, hit me up for a beer and I'll mime it for you.)
Second, when they starve, the cells tend to aggregate into pellets of thousands of entangled cells, called a biofilm. When they do so, they usually keep elongating but stop fully dividing, forming long filaments.
And these two simple things are all it takes for the cells climb the gradient. Can you guess what the emergent property is?
...
...
...
Notice that if a cell-filament is entangled with others, then its poles are stuck and can't rotate. As the cells keep growing in a twisted way, eventually this happens:
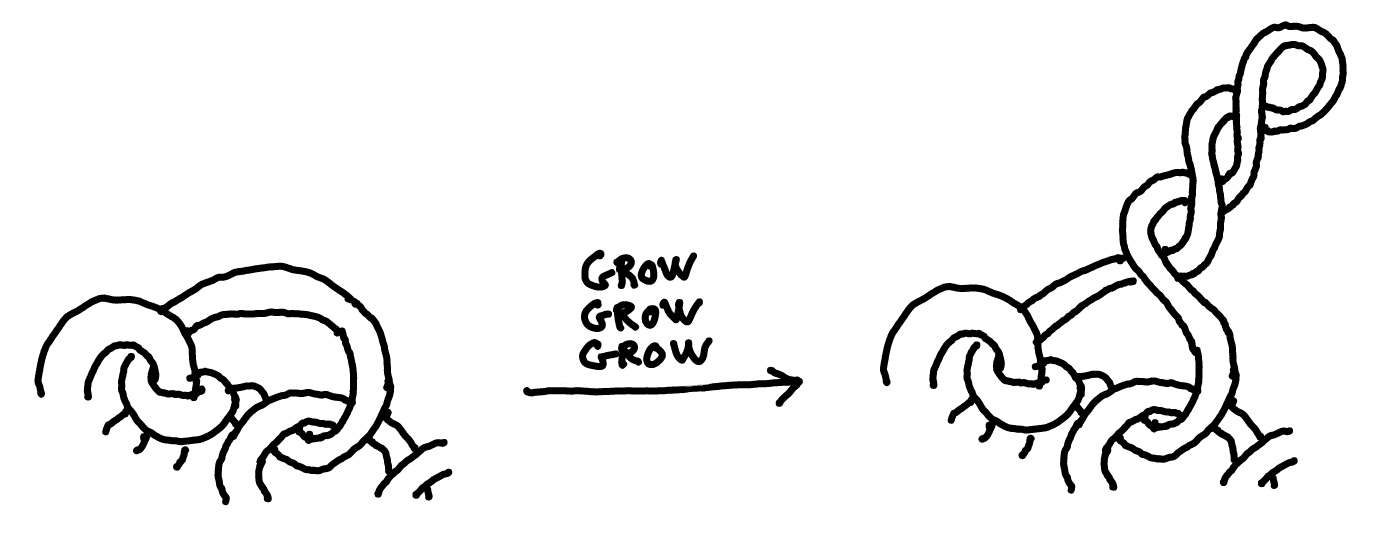
And so our clump of bacteria, while sticking firmly to surfaces, now has tentacles it can extend to reach for oxygen, as if surrounded by snorkels. Here's an actual picture:
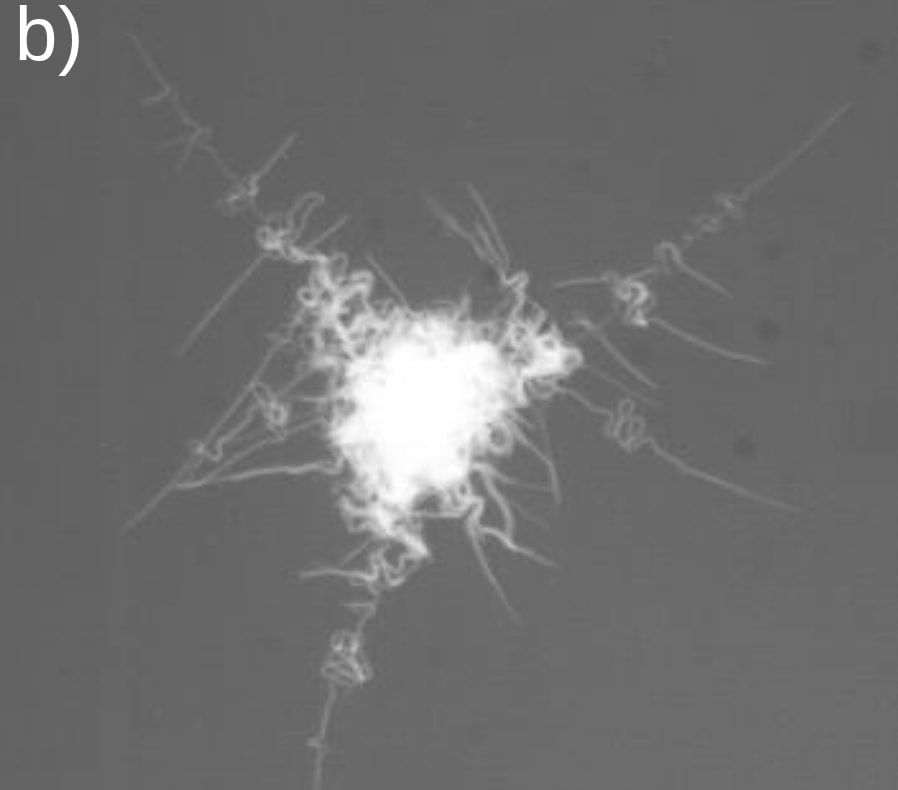
Now, if there is more oxygen on one side, the cells who have access to the most oxygen will grow faster, so the new tentacles will predominantly occur on the well-oxygenized side of the colony. In other words, the colony throws its tentacles preferentially in the direction of the oxygen source.
The chained cells at the end of the tentacles can then complete their division, allowing to start the process again in the new location. And that's how, the authors say, B. subtilis' biofilms can escape crowded environments by tracking the oxygen gradient. It's basically performing gradient descent, just by combining twisted cell growth, chaining and entanglement.
The paper only demonstrates this for oxygen, but the filament tentacles don't explicitly rely on any oxygen detector. I suppose it would work just as well to track down food, flee antibiotics, or seek better temperatures. That's the elegant part: it's a pure growth-maximizer that is driven by growth itself. The map is actually the territory.
This kind of mechanism is why I think studying bacteria is so fun. Bacteria do this kind of things all the time. When your genome can only store 1.25 MB of information, you can't waste any of it on clear, rational, legible mechanisms. Rather, bacteria's engineering approach is to throw together some spooky dynamical system that somehow couples the thing you want to maximize to the behavior that maximizes it, with fewer moving parts than what seems possible.
(If you want another example, here's one that is built on pure math.)
The future of non-human design
To come back to the question I raised at the beginning – does this tell us anything about what kind of inventions the super-intelligent AIs of the future will come up with?
What's pretty clear is that living organisms are the product of some very peculiar constraints, including constraints that directly emanate from the very process of evolution. AI-assisted design will not have any of these constraints, so the design space is much larger. I sometimes hear things like "[scary thing] doesn't occur in nature, so [scary thing] is impossible", and that sounds definitely wrong – evolution operates under specific constraints that apply only to evolving things. All natural pandemics are subject to these constraints, but artificial bioweapons might not be.
On the other hand, the living world contains some of the world's most fascinating mechanisms, and it would be really hard to come up with them through intelligent design. It's possible that the best parts of the design space are simply too strange, too far-fetched, to be explored by a rational agent. Maybe some designs can only be found by relentless real-world experimentation.
Machines may already beat us at PhD-level math, but it will take more time before they can fully harness the vast powers of accidental discovery. Only then will they be able to truly rival Nature.

- ^
For the zoomers among you: floppy disks were popular storage devices until the early 2000s - that's what the 💾 save icon is supposed to represent. I can feel my bones rotting and crumbling like ancient ruins as I'm writing this.
- ^
You are welcome to implement this website. Suggested name: X-chromosome
I could be way off on this, but I cannot help but core here is less about complexity than it is about efficiency. The most efficient processes do all appear to be a bit simpler than they probably are. It's a bit like watching an every talented craftsman working and thinking "The looks easy." Then when you try you find out it was much more difficult and complicated than it appeared. The craftsman's efficiency in action (ability to handle/deal with the underlying complexity) masked the truth a bit.