Admittedly this sounds like an empirical claim, yet is not really testable, as these visualizations and input-variable-to-2D-space mappings are purely hypothetical
Usually not testable, but occasionally reality manages to make it convenient to test something like this fun paper.
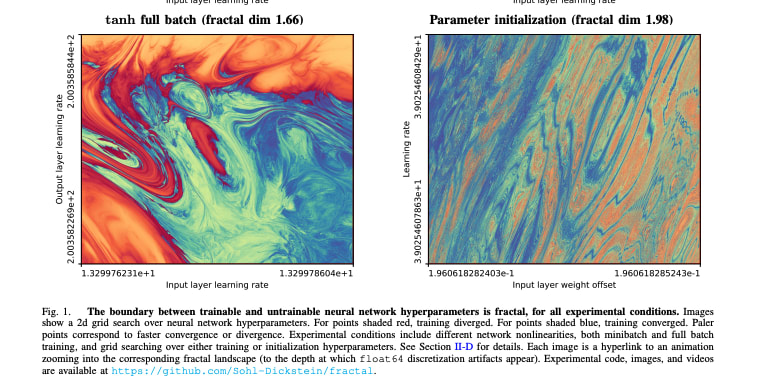
1Tl;dr: Much of common sense and personal insights are just first order approximations, broadly generalizing complex situations to a single supposed truth. But often the truth value of a claim depends on many hidden factors. In this post I argue that it’s important to maintain a general awareness of the imprecise nature of seemingly binary statements, and to recognize when it’s appropriate to dig deeper and figure out these hidden variables and how they interact. Often we should replace “Is X true?”-type questions with “When is X true?”, which has a better shot at leading to more interesting and accurate insights.
Many human disagreements come down to something like the following:
Alan: Did you know, Earth's surface is water?
Betty: What, that is not true! We are standing on Earth right now, and it is clearly not wet.
Alan: Well this is just anecdotal evidence. Haven't you read the science that most of Earth's surface is covered by water?
Betty: Of course I know this science. But surely you don't believe it is water all the way down? Do you know the science that beneath all this water, there is actually a lot of rock at the ground? So Earth's surface is solid after all.
...
Why is this argument so silly? Alice and Bob argue about "the Earth's surface" as a single thing, such that claims about it, e.g. what material it consists of, can be answered in a binary fashion. But whether or not that is true or false is not a well-defined question that one can just answer. It depends not only on your exact definitions but also, crucially, on many implicit, even hidden factors. In this case, your exact location on the planet, as well as e.g. the time of year.
Of course nobody would have that exact argument, because in this context the futility of it becomes instantly obvious. Yet, many other arguments, as well as individual misconceptions, are of a very similar nature, where a complex question that depends on many hidden factors is falsely treated as a binary one.
Note that even probabilistic or grayscale thinking are often not sufficient to resolve this, because they still treat the question as one that essentially has one answer. Replacing the binary with a spectrum or probability is often an improvement, but it doesn’t address the inherent hidden complexity of most statements.
I once had a conversation with a friend of mine, which went roughly like this:
Bob: “I’ve been trying to gain weight, but it seems impossible.”
Alice: “Have you tracked your calorie intake?”
Bob: “Yes, pretty much, and I’m averaging ~2800kcal per day, which should be quite a bit more than I would need to maintain my weight.”
Alice: “So are you weighing everything and calculating the calories based on the exact quantities?”
Bob: “Not quite, I’m often rather eyeballing it and going with my best guess, as weighing everything would add a lot of overhead, which I think isn’t necessary as these guesses should be pretty solid.”
Alice: “People can’t estimate calories. There have been studies on that.”
Bob: “...uhh… this claim seems rather overconfident and one-dimensional, and one day I will mention it in a post.”
Of course it’s possible that my friend here was right in the sense that really my calorie tracking was simply off, and my real calorie intake was lower than I thought, and this explained my failure to gain any weight[1].
But what I’m much more interested in now[2] is the claim “People can’t estimate calories. There have been studies on that”. This seems to be exactly the kind of thing where some claim is accepted as “True”, because there’s evidence for it, without taking into account that it depends on (hidden) factors, and hence is sometimes true and sometimes false (and maybe sometimes even somewhere in between).
I’m sure there’s indeed some general bias that has to be overcome when estimating one’s calorie intake. And it may take some effort to get calibrated. But my friend here basically claimed that it’s somehow fundamentally impossible to overcome that bias and to get calibrated in this domain[3].
So, can people estimate their caloric intake? I would guess it mainly depends on training and experience. Maybe there is this general bias, either of people generally underestimating calorie counts, or of people being influenced by wishful thinking depending on their goals. But if you’re aware of this bias and go through some deliberate training to get calibrated, then I don’t see a reason for that not to just work. Some noise remains of course, and this you could indeed reduce by precisely weighing all the ingredients of your food, but this noise would cancel out over time and your estimates hence should be sufficiently precise to control your caloric intake pretty well.
Nudging is a form of “choice architecture”, where people’s decisions are (supposed to be) influenced by subtle changes in how options are presented to them. E.g. by adjusting the order or framing of decision options, or selecting different defaults. Does nudging work? There’s a wild debate with people saying yes or no or yes but not as much as we initially thought but still it may be a valuable policy tool. But, given how valuable nudging may be for policy, and how important it hence would be to properly understand it, it’s much more fruitful to ask: when and why does it work (and how well exactly), and when does it not? Because that it works at all – in the sense of: there are at least some cases where this has a systematic non-zero effect on people’s behavior – should be obvious (but maybe it’s just me). And luckily, there are people out there engaging with that exact question:
We can start to see the bigger problem here. We have a simplistic and binary “works” versus “does not work” debate. But this is based on lumping together a massive range of different things under the “nudge” label, and then attaching a single effect size to that label.
Similar problems exist for many study findings: some general effect is found by an initial study, then it’s either reliably replicated, or replications fail. Depending on that, most people are happy to accept its findings as The Truth in the first case, or denying the effect’s existence altogether in the second case. If they accept the effect’s existence, they then usually make the mental shortcut of assuming that it just applies, for everyone, everywhere, all the time[4]. In reality, nearly all these findings remain subject to various factors and can differ significantly. Variables such as the specific implementation, the target audience, the weather, or the time of year can all influence the outcomes to varying degrees.
Take power posing for instance: it certainly does not live up to the initial hype, but it may still be worth asking: who benefits from it, and when? Maybe this would actually make a notable difference when you are feeling down? Or maybe it wouldn’t. But simply asking “does it work” is and remains a rather misleading question most of the time, as it just sweeps away the many things in life where the answer will not be a binary (or even one-dimensional) one[5].
Probably the best way to get the point of this post across is to put it into pictures. So let’s do that. If “true” is blue, and “false” is orange, then most people go through life with basically these two buckets:
And most binary-sounding claims would be sorted into either of them.
Then some come across the ideas of probabilistic or grayscale thinking, and end up with a finer spectrum:
And now, binary-sounding claims would not just be seen as “true” or “false”, but in finer shades of uncertainty and nuance.
But still, at this point, for many people a claim will still essentially occupy a point on that spectrum. Whereas I would argue that many claims actually make up a whole landscape on their own[6], similar to “is Earth’s surface water or earth”:
And this landscape is even “fractal” in the sense that you could in principle zoom in quite a lot and would find more and more detail, similar to a fractal zoom or a coastline. Admittedly this sounds like an empirical claim, yet is not really testable, as these visualizations and input-variable-to-2D-space mappings are purely hypothetical. But the intuition behind it is this: quite often, for any set of operationalizations that seem to lead to a “true” or “false” evaluation, you can come up with one extra detail that flips the answer to the opposite. For instance, is broccoli healthy?
And so forth. Each of these steps is like a zoom in closer to the border of the fractal, and in each step you can find further conditions that lead to the claim being true or false. It just keeps going. Of course “zooming in” so much is not very practical – but I’m mostly intending to describe the territory here, without claiming that we should zoom in on it that much in practice and always model all these little details in our map. Whether it’s worthwhile to look at reality in such detail still very much, who would have guessed, depends on many factors.
Now, to get back to the earlier question “does power posing work”? Maybe here the landscape would look somewhat like this:
This landscape would suggest that it’s mostly useless, but if you can find easy ways to systematically identify the conditions where the effect is >0, and if the effect happens to be large enough to be worth the 30 seconds of just standing there, then it may be a useful thing to utilize every now and then. Don’t judge a tool by its average output if there are systematic ways to benefit from it beyond the average.
I’m not saying you should now all run to the next mirror, power pose in front of it and see what happens (but feel free, of course). What I’m rather trying to say is: if somebody tells you they love power posing, and they do it every morning, and it helps them a lot to feel more energetic and confident, then please don’t start arguing with that person because "studies show that it doesn’t work and hence they are irrational"[7].
Of course the solution can’t be to always see everything at the maximum possible level of detail and nuance. Often, due to lack of studies, or computing power, or a number of other reasons, we lack the necessary insight to be able to tell what that landscape actually looks like.
I’ve heard before that many superforecasters know about Bayesian updating, yet rarely, if at all, explicitly do the actual math involved. They rather get a general feel for it to incorporate it into their world model on a more intuitive level. I suspect the same applies here: it’s less about running through life with a magnifying glass, trying to figure out all the details about the fractal reality all around us, and more about getting an intuitive appreciation of the idea. This way, when your nephew asks you whether broccoli is healthy, you can just say “yes” rather than overwhelming him with a lecture on the many factors that determine the answer to this question. But when you think about an important study result, or the efficient market hypothesis, or some large scale intervention or policy proposal, or – heaven forbid – a debate in the lesswrong comments section, you have the presence of mind to not fall for the seductive simplicity of binary answers, but to look for the factors that determine the answer.
Thanks to Adrian Spierling and Francesca Müller for providing valuable feedback on this post.
Even though I quite doubt it, and think I rather underestimated my calorie expenditure instead. Ultimately my attempts succeeded, and the winning strategy for me happened to be to drop calorie tracking altogether and instead track my weight on a daily basis.
...surely not at all because that’s the point where I suspect the other person was wrong, and not me
Now to be fair, this is almost certainly not exactly what she meant, and “People can’t estimate calories” was rather meant as a short version of “Studies show that most people are systematically wrong in their calorie estimates, so this is a likely explanation for your struggles” that was just phrased a bit uncharitably. But let’s ignore that point, so that I have some strawman view that I can properly attack
When explicitly asked about this, most people would probably not defend this view, and acknowledge context dependence. But when not prompted in such a way, this is pretty often overlooked.
Even though I do acknowledge that as far as study designs are concerned, it does make sense to focus on the “is the effect real at all” question. It’s more the interpretations of the results of such studies that I tend to disagree with.
For this, let’s just assume we mapped all the “hidden input variables” onto a square-shaped 2D space using something like t-SNE
The exception here maybe being: if this person is not just personally excited about what it does for them, but also runs around convincing everyone else to start power posing because it’s such an amazing tool, then it may indeed make sense to inform them that they are most likely an outlier in how much they benefit from it, and other people will on average benefit much less, or not at all, from this intervention.
