That's entirely fair. And tbh most of the time I'm looking at a hot loop where the compiler did something dumb, the first question I ask myself is "is there some other way I could write this code so that the compiler will recognize that the more performant code is an option". Compilers are really quite good and fully featured these days, so there usually is some code transformation or pragma or compiler flag that will work for my specific use case.

Generating a loud noise that you're expecting but your opponents aren't might be even better at differentially elevating their heart rates.

The point with assembler in drawing the analogy "assembly programmers : optimizing compilers :: programmers-in-general : scaffolded LLMs". The post was not about any particular opinions I have^[1] about how LLMs will or won't interact with assembly code.

As optimizing compilers became popular, assembly programmers found that their particular skill of writing assembly code from scratch was largely obsolete. They didn't generally beome unemployed as result though. Instead, many of the incidental skills they picked up along the way^[2] went from."incidental side skill" to "main value proposition".

1. ^{^}

   I do have such opinions, namely "LLMs mostly won't write as for basically the same reasons humans don't write much asm". But that opinion isn't super relevant here.

2. ^{^}

   e.g. knowing how to read a crash dump or which memory access patterns are good or just general skill at translating high-level descriptions of program behavior into a good data model and code the correctly operate on those data structures

My thesis is approximately "we don't write assembly because it usually doesn't provide much practical benefit and also it's obnoxious to do". This is in opposition to the thesis "we don't write assembly because computers have surpassed the abilities of all but the best humans and so human intervention would only make the output worse".

I think this is an important point because some people seem to be under the impression that "LLMs can write better code than pretty much all humans" is a necessary prerequisite for "it's usually not worth it for a human to write code", and also operating under the model of "once LLMs write most code, there will be nothing left to do for the people with software development skills".

Drop in remote worker

I think this one sounds like it describes a single level of capability, but quietly assumes a that the capabilities of "a remote worker" are basically static compared to the speed of capabilities growth. A late-2025 LLM with the default late-2025 LLM agent scaffold provided by the org releasing that model (e.g. chatgpt.com for openai) would have been able to do many of the jobs posted in 2022 to Upwork. But these days, before posting a job to Upwork, most people will at least try running their request by ChatGPT to see if it can one-shot it, and so those exact jobs no longer exist. The jobs which still exist are those which require some capabilities that are not available to anyone with a browser and $20 to their name.

This is a fine assumption if you expect AI capabilities to go from "worse than humans at almost everything" to "better than humans at almost everything" in short order, much much faster than the ability of "legacy" organizations to adapt to them. I think that worldview is pretty well summarized by the graph from the waitbutwhy AI article:

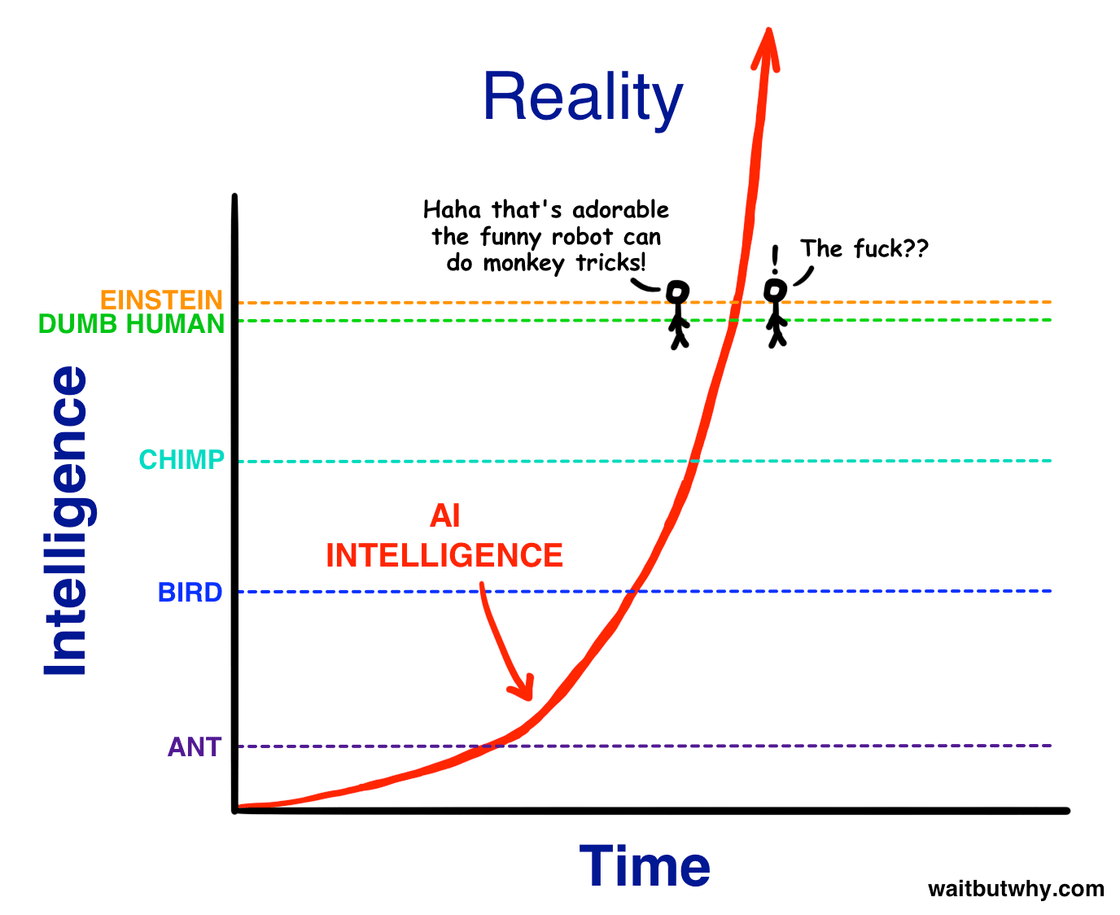
But if the time period isn't short, we may instead see that "drop-in remote worker" is a moving target in the same way "AGI" is, and so me may get AI with scary capabilities we care about without getting a clear indication like "you can now hire a drop-in AI worker that is actually capable of all the things you would hire ahuman to do".

But this was misdirection, we are arguing about how surprised we should be when a competent agent doesn't learn a very simple lesson after making the mistake several times. Optimality is misdirection, the thing you're defending is extreme sub-optimality and the thing I'm arguing for is human-level ability-to-correct-mistakes.

I agree that this is the thing we're arguing about. I do think there's a reasonable chance that the first AIs which are capable of scary things^[1] will have much worse sample efficiency than humans, and as such be much worse than humans at learning from their mistakes. Maybe 30%? Intervening on the propensity of AI agents to do dangerous things because they are overconfident in their model of why the dangerous thing is safe seems very high leverage in such worlds.

I think focusing on the "first AI smart enough" leads to a lot of low-EV research. If you solve a problem with the first AI smart enough, this doesn't help much because a) there are presumably other AIs of similar capability, or soon will be, with somewhat different capability profiles and b) it won't be long before there are more capable AIs and c) it's hard to predict future capability profiles.

a. Ideally the techniques for reducing the propensity of AI agents to take risks due to overconfidence would be public, such that any frontier org would use them. The organizations deploying the AI don't want that failure mode, the people asking the AIs to do things don't want the failure mode, even the AIs themselves (to the extent that they can be modeled as having coherent preferences^[2]) don't want the failure mode. Someone might still do something dumb, but I expect making the tools to avoid that dumb mistake available and easy to use will reduce the chances of that particular dumb failure mode.

b. Unless civilization collapses due to a human or an AI making a catastrophic mistake before then

c. Sure, but I think it makes sense to invest nontrivial resources in the case of "what if the future is basically how you would expect if present trends continued with no surprises". The exact unsurprising path you project in such a fashion isn't very likely to pan out, but the plans you make and the tools and organizations you build might be able to be adapted when those surprises do occur.

Basically this entire thread was me disagreeing with

> Trying to address minor capability problems in hypothetical stupid AIs is irrelevant to x-risk.

because I think "stupid" scary AIs are in fact fairly likely, and it would be undignified for us to all die to a "stupid" scary AI accidentally ending the world.

1. ^{^}

    Concrete examples of the sorts of things I'm thinking of:

   • Build a more capable successor
   • Do significant biological engineering
   • Manage a globally-significant infrastructure project (e.g. "tile the Sahara with solar panels")
2. ^{^}

   I think this extent is higher with current LLMs than commonly appreciated, though this is way out of scope for this conversation.

What baby gate protects you from Claude subtly misspecifying all your unit tests

Huh. This is an interesting question, since it feels tractable. Performing the exercise of "sit down with a clock and think for 5 minutes".

So here are some things which I think would help:

1. Never allow a single (wlog) Claude instance modify both the tests and the unit under test within the same task. Tasks may look like
   • "Here's an item of the spec which hasn't been implemented yet, write a test and ensure it fails"
   • or "Here's an observed bug, write a test which reproduces the bug and ensure the regression test fails"
   • or "Here's a failing test, fix the unit under test and ensure that tests pass"
   • but never "Here's an observed bug, figure out what happened, fix it, and write a test to ensure it can't happen again"
2. Have Claude write some example-based tests: these are your classic assert 5 == add(3, 2) style tests. The important thing is that the left hand side of the assert, and all args to the unit on the test, are primitives or composed from primitives.
3. Have Claude write some property-based tests. These tests specify some property which should hold over all inputs to the unit under test. For example, you could have @given(left=st.integers(min_value=1), right=st.integers(min_value=1)) annotation on def test_add_two_positives_gt_left(left, right): assert add(left, right) > left.
4. Do Mutation testing: take the unit under test, and the AI-generated test suite, and then make changes ("mutants") of the type that common coding errors tend to be (replacing if a > b: foo(a) with if a < b: foo(a) or if a > b: foo(b) etc) for thousands of examples, and checking how many of the "mutants" your test suite catches
5. Have a more trusted, less capable agent sanity-check the tests from 2 and 3. For extra oomph:
   • Give it a list of the tests, ordered by Shapley value of mutants killed or such^[1]
   • See if it can improve on the tests, by the above. Improving an existing test suite is often easier than writing it from scratch.
   • Give it some examples of mutants not killed by any tests, or not killed by any of the top N tests. See if those mutants suggest more test cases.

Of the things I list here, I do 1 and 2 as standard practice at $DAYJOB. I do those mostly because those practices help with catching mundane mistakes: I don't particularly expect Claude to write intentionally bad tests. Still, I expect those practices would also help if I was having an actively-malicious Claude instance write tests for me^[2]. If the Claude wants to ship code that's bad in some specific way with unit tests deliberately engineered not to expose that badness, these mitigation strategies would make evil!Claude's job much harder.

On examination, these proposals share a basic thread which looks something like "make writing subtly-misspecified tests harder faster than you make writing correct tests harder". Claude is better than I am at writing tests, or at least will be at some point in the near future. But there are limits to Claude's abilities - if you can get to the point where Claude can just barely do the task, it won't be able to do the task and also secretly accomplish some other goal which makes the task harder^[3].

More generally, if you want an autonomous agent it must be self monitoring and self evaluating

I don't think this is true. The most effective human organizations have people in separate roles. That's not just for comparative advantage reasons. You want dev and QA to be different people. Likewise your salespeople should probably not be the same people writing the queries that say whether the thresholds for bonuses have been met. Sometimes you even want one person to operate in multiple roles sequentially, e.g. in red-green-refactor^[4] development flows.

An actually autonomous agent has to be able to ontologize reward over the computable environment in a general way that doesn't require some other mind to come in and correct it all the time. If you don't have that, you're not getting meaningful autonomy.

I note that public companies usually don't leave anyone operating without accountability to^[5], and correction from someone else associated with the company. I doubt that your actual position is "human employees are not actually autonomous agents", though.^[6] Is your position that, if you need to erect so many safeguards against reward hacking, you'll approximately always be better off just doing the task yourself, and so you can't get meaningful work out of agents that reward hack?

1. ^{^}

   As far as I can tell, no tooling exists for this at this time. I kind of want to build such tooling, and am actively restraining myself because the automated test generation rabbit hole goes arbitrarily deep and I have already wasted multiple weeks of my professional life chasing those rabbits with lackluster results (as reliability at that level is just not that important for the code I write at $DAYJOB)

2. ^{^}

   Well, would help against the particular threat model of subtly bad unit tests. When I wrote the phrase "having an actively-malicious Claude instance write tests for me", my immediate reaction to my own words was to note that that's a fancy way of saying "I have given a malicious Claude instance the ability to write and execute code on my machine".

3. ^{^}

   Unless Claude is sandbagging, but at that point you just have an elicitation problem, and that's the sort of problem the ML community is already quite good at solving^[7].

4. ^{^}

   Or the ever-popular "red-green-ship" development flow

5. ^{^}

   As long as AI agents don't meaningfully have accountability, I don't think it's even desirable for them to have "actual autonomy". Sure, a Claude instance who tries to sabotage the unit tests to slip bad code under the radar might cause the class of all scaffolded Claude agents as a whole to lose some credibility, but that particular Claude instance is ephemeral and none of the future instances will even remember that it happened or learn that doing that is against their interests.
   
   This is now way way outside the scope of the original comment though.

6. ^{^}

   Specifically, if your definition of "actually autonomous" excludes humans, I don't understand why we care whether an agent is "actually autonomous". If that is your position, though, I'd be curious whether you have particular capabilities in mind which would be unlocked by an agent with that level of autonomy, but would not be unlocked by a group of human-level-autonomous agents,

7. ^{^}

   I don't particularly expect the ML community to solve the elicitation problem elegantly but it does seem like the sort of problem which can be distilled down to a numeric score. The ML community has an extremely strong track record of making numeric scores go up. I would bet money they could make this number go up too.

Ideally this is true whether it's in a simulation or real life

Agreed. In practice, though, I worry that if you make it salient that sometimes AIs do ambiguously immoral things in situations where they thought they were being tested on ability to accomplish a goal but were actually being tested on propensity to behave morally, AI companies will see that and create RL envs to better teach AI agents to distinguish cases where the testers are trying to elicit capabilities from cases where testers are trying to elicit moral behavior.

I think it should be the AI Lab's job to filter out that kind of data from the next training run.

I agree normatively, but also that sentence makes me want a react with the mood "lol of despair".

I don't think "check whether the situation you're in looks like a morality test and, if so, try to pass the morality test" is a behavior we want to encourage in our LLM agents.