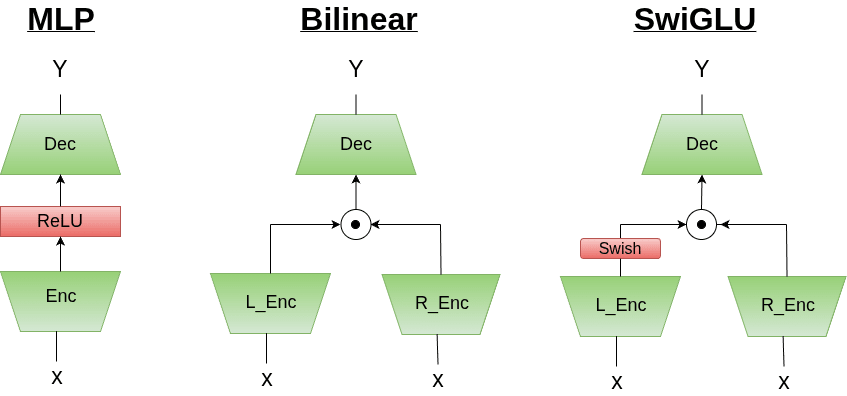
I'm confused on what you're referring to. Bilinear layers are scale invariant by linearity

B i l i n e a r (a x) = a^{2} B i l i n e a r (x)

So x could be the input-token, a vector d (from the previous bilinear layer), or a steering vector added in, but it will still produce the same output vector (and affect the same hidden dims of the bilinear layer in the same proportions).

Another way to say this is that for:

y = B i l i n e a r (a x)

The percentage of attribution of each weight in bilinear w/ respect to y is the same regardless of $a$ , since to compute the percentage, you'd divide by the total so that cancels out scaling by $a$ .

This also means that, solely from the weights, you can trace the computation done by injecting this... (read more)

Replying toTensor-Transformer Variants are Surprisingly Performant

Logan Riggs4d

Tensor-Transformer Variants are Surprisingly Performant

I hadn't considered steering vectors before, but yes that's correct.

Replying toTensor-Transformer Variants are Surprisingly Performant

Logan Riggs1mo

Tensor-Transformer Variants are Surprisingly Performant

Just looking at Shazeer's paper (Appendix A)

All of the GLU models performed better (lower is better) and the GLU models have a bilinear encoder (just w/ & w/o a sigmoid/GeLU/Swish/ReLU function). So in fact it does better (if this is what you meant by a dual encoder).

HOWEVER, we could have 3 encoders, or 100! This should store even more information, and would probably perform better per step, but would take up more GPU VRAM and/or take longer to compute each step.

In this post, though, I used wall clock time as a measure of training efficiency. Hand-wavy:

loss/step * time/step

(maybe it should be divided to make it loss/time?)

Replying toTensor-Transformer Variants are Surprisingly Performant

Logan Riggs1mo

Tensor-Transformer Variants are Surprisingly Performant

A full 3rd order tensor is much larger, whereas this parametrization is the CP-decomposition form. This is the "official reason" when I'm really just building off Dooms et al. (I've never actually tried training the full tensor though!)

Re init: the init for modded gpt at that fork was kind of weird, but I'm pretty sure most standard inits prevent that. I am using RMSNorm which can be treated as a tensor network as well (I could maybe dm explanation, it's a forthcoming resource from Thomas). I'm also normalizing Q & K which isn't a tensor network, BUT compositionality is on a spectrum (maybe I am too). So this does mean a small portion of the model isn't a tensor network.

Ideally we can work around this!

Replying toTensor-Transformer Variants are Surprisingly Performant

Logan Riggs1mo

Tensor-Transformer Variants are Surprisingly Performant

Yep! But I do think the highest priority thing would be actually doing ambitious interp w/ this, although, if we had 100 people working on this (instead of ~4-5 full time?), a few working on the scaling laws would be good.

TNs are more amenable to optimizing exactly what we want in a mathematically precise way, so optimizing for this (to achieve ambitious mech interp) would incur an additional cost in capabilities, just fyi.

Tensor-Transformer Variants are Surprisingly Performant

Logan Riggs

1mo

I've been researching tensor networks as a more interpretable architecture, but whenever I tell people this, they always ask "But is it any good?"

So I trained multiple 500M parameter LLMs on fineweb, showing the tensor variant needed ~4% more batches of data to match CE-loss.

There's a few caveats, so my personal estimate is around 15% worst to 10% better. Details below.

The Architecture

Replacing MLP w/ a Bilinear Layer

An MLP is a linear encoder, ReLU, then linear decoder.

M L P (x) = D (R e L U (E (x)))

A bilinear layer asks "what's better than one encoder? Two!"

B i l i n e a r (x) = D (L x ⊙ R x)

Where $⊙$ means "element-wise multiply" eg

[1, 2, 3] ⊙ [1, 2, 3] = [1, 4, 9]

A SwiGLU Layer (Swish Gated Linear Unit) says "Let's add in nonlinearities"

S w i G L U (x) = D (s w i s h (L x) ⊙ R x)

SwiGLU is a SOTA architecture & Bilinear is a tensor network.

Replacing Softmax Attn w/

... (read 1135 more words →)

Replying toARC progress update: Competing with sampling

Logan Riggs3mo

ARC progress update: Competing with sampling

Not claiming to understand your work, but my intuition is that a bilinear layer would be easier to prove things about than an MLP, while also being closer to SOTA. Some (maybe) useful properties for your case:

bilinear
- directions are what matters for relationships between components (between any part of any matrix, where the input can be considered just another matrix); scale doesn't affect compositionality.
- No implicit computation (eg different polytopes of MLPs), just the structure in the weights.
a polynomial
can be turned into a tensor (& combined into a larger tensor when you have multiple layers)
- Note: a bilinear layer is already a CP decomposition (generalization of SVD, maintaining the outer product format), but combining two

... (read more)

Temporarily Losing My Ego

Logan Riggs

4mo

I was doing the online version of the Jhourney retreat where they try to teach you the jhanas (narrator: he did not learn the jhanas). Part of what wsas taught was to work on your curiousity, which I chose to practice noticing surprisal.

It's ~impossible to predict low-level details of vision. I can predict high level details ("oh that car will still be there in the next time step"), but not low level details ("oh the exact colors and texture will be like this").

This also extended to hearing (specifically the exact fluctuations of sounds) and same w/ my body sensations. So these modalities made a good warm-up or "easy mode".

The meditation retreat was... (read 881 more words →)

Logan Riggs4mo

Great work!

Listened to a talk from Philipp on it today and am confused on why we can't just make a better benchmark than LDS?

Why not just train eg 1k different models, where you left 1 datapoint out? LDS is noisy, so I'm assuming 1k datapoints that exactly capture what you want is better than 1M datapoints that are an approximation $.$ ^[1]

As an estimate, Nano-GPT speedrun takes a little more than 2 min now, so you can train 1001 of these in:

2.33*1k/60 = 38hrs on 8 H100's which is maybe 4 b200's which is $24/hr, so ~$1k.

And that's getting a 124M param LLM trained on 730M tokens up to GPT2 level. Y'all's quantitative setting... (read more)

Replying toPenny's Hands

Logan Riggs4mo

Penny's Hands

I was actually expecting Penny to develop dystonia coincidentally, and the RL would tie-in by needing to be learned in reverse ie optimizing from dystonic to normal. It is a much more pleasant ending than the protagonist's tone the whole way through.

If I was writing a fanfic of this, I'd keep the story as is (+ or - the last paragraph), but then continue into the present moment which leads to the realization.

Replying toFinding Features in Neural Networks with the Empirical NTK

Logan Riggs4mo

Finding Features in Neural Networks with the Empirical NTK

It's very exciting to have an orthogonal research direction that finds these ground truth features, which might possibly even generalize(!!). Please do report future results, even if negative (though your Malladi et al link is some evidence in the positive).

It's also very confusing since I'm unsure how this all fits in with everything else? This clearly works in these cases. SAE's clearly work in some cases as well (and same w/ the parameter decomposition research), but what's the "Grand Theory of NN Interp" that explains all of these results?

In general, I believe it's very important that we hedge our bets on research directions for interp. The main reason being one of them actually panning out, but even if not, they already provide unique pieces of evidences for later researchers (maybe us, maybe LLMs, lol) to hopefully figure out that "Grand Theory of NN Interp".

Replying toHospitalization: A Review

Logan Riggs4mo

Hospitalization: A Review

Thanks Charlie:)

Hospitalization: A Review

Logan Riggs

4mo

I woke up Friday morning w/ a very sore left shoulder. I tried stretching it, but my left chest hurt too. Isn't pain on one side a sign of a heart attack?

Chest pain, arm/shoulder pain, and my breathing is pretty shallow now that I think about it, but I don't think I'm having a heart attack because that'd be terribly inconvenient.

But it'd also be very dumb if I died cause I didn't go to the ER.

So I get my phone to call an Uber, when I suddenly feel very dizzy and nauseous. My wife is on a video call w/ a client, and I tell her:

"Baby?"

She's probably annoyed at me interrupting; I... (read 2481 more words →)

366

•••

Replacing RL w/ Parameter-based Evolutionary Strategies

Logan Riggs

4mo

I want to highlight this paper (from Sept 29, 2025) of an alternative to RL (for fine-tuning pre-trained LLMs) which:

Performs better
Requires less data
Consistent across seeds
Robust (ie don't need to do a grid search on your hyperparameters)
Less "Reward Hacking" (ie when optimizing for conciseness, it naturally stays close to the original model ie low KL-Divergence)

They claim the magic sauce behind all this is the evolutionary strategy optimizing over distributions of model parameters. Surprisingly, they've scaled this to optimize over billion-parameter models.

Let's get into their method.

Evolutionary Strategy (ES) Algorithm

They start w/ a "Basic ES Algorithm" which is:

In other words, we're gonna sample noise around the original model's weights N times (ie we're going to... (read 792 more words →)

Telling the Difference Between Memories & Logical Guesses

Logan Riggs

4mo

Witness testimonies have been shown to be pretty unreliable. Many innocent people have been convicted based off eye-witness testimony, which was overturned by DNA evidence. One interesting example is from Buckhout in 1980, provocatively titled "2000 witnesses can be wrong"

Buckhout performed an experiment with 2,145 at-home viewers of a popular news broadcast. The television network played a 13-second clip of a mock robbery, produced by Buckhout. In the video, viewers watched a man in a hat run up behind a woman, knock her over, and take her purse. The perpetrator's face was only visible for about 3.5 seconds. The clip was followed by the announcer asking participants at home for cooperation in

... (read 922 more words →)

Making Your Pain Worse can Get You What You Want

Logan Riggs

4mo

I remember going to church w/ my mom where we'd need to stand while singing. I didn't really like standing that long, so I told Mom my legs were hurting so could I please sit down?

She said yes.

Sooo the next week, when I wanted to sit down, I intentionally tensed my knee-area so that my legs would hurt. Then I could tell ask my mom again and sit down while not being a dirty liar (we were in church after all).

In general, people can sometimes get what they want [attention/emotional support/etc] by making their problems worse (or creating a problem when there's none there). One simple way to achieve this is to... (read 840 more words →)

How to Feel More Alive

Logan Riggs

4mo

Cached responses are very useful. When this topic comes up, I bring up X. When the gadget comes by, I add a gizmo to it. When you have a repetition of three, come up with a pattern-breaking, funny example for the last one.

But to have most of your words & actions to be cached is considered soul crushing.

Is to be dead.

Oh, so you're saying to just be more sPonTanEOus?

Sort'of! But "just be spontenanoeous" isn't helpful advice or even spelled correctly. The key is to become aware of:

Local Details Unique to Your Current Situation

In any long-term relationship, it's easy to fall into the same routines & canned responses. With my wife^[1], making the... (read 1013 more words →)

Looking for feature absorption automatically

Theodore Ehrenborg

Theodore Ehrenborg, Logan Riggs, Cleo Nardo

6mo

Summary

This post discusses a possible way to detect feature absorption: find SAE latents that (1) have a similar causal effect, but (2) don't activate on the same token. We'll discuss the theory of how this method should work, and we'll also briefly go over how it doesn't work in practice.

Introduction

Feature absorption was introduced in A is for Absorption.

Their example: Assume the model has two features, 𝒜="this token is 'short'" and ℬ="this word starts with s". In the prompt "Sam is short", 𝒜 activates on "short", and ℬ activates on "Sam" and "short". Hence the L0 across those two features is 3. We train an SAE to recover these features.

But the SAE is... (read 1594 more words →)

Stores Already Have Empty Shelves.

Just saw two empty shelves (~toilet paper & peanut butter) at my local grocery store. Curious how to prepare for this? Currently we've stocked up on:
1. toilet paper
2. feminine products
3. Canned soup (that we like & already eat)

Additionally any models to understand the situation? For example:

Self-fulfilling prophecy - Other people will believe that toilet paper will run out, so it will
Time for Sea Freights to get to US from China is 20-40 days, so even if the trade war ends, it will still take ~ a month for things to (mostly) go back from normal.

How do you work w/ sleep consolidation?

Sleep consolidation/ "sleeping on it" is when you struggle w/ [learning a piano piece], sleep on it, and then you're suddenly much better at it the next day!

This has happened to me for piano, dance, math concepts, video games, & rock climbing, but it varies in effectiveness. Why? Is it:

Duration of struggling activity
Amount of attention paid to activity
Having a frustrating experience
Time of day (e.g. right before sleep)

My current guess is a mix of all four. But I'm unsure if you [practice piano] in the morning, you'll need to remind yourself about the experience before you fall asleep, also implying that you can only really consolidate 1... (read more)

Implications of a Brain Scan Revolution

Suppose we were able to gather large amounts of brain-scans, lets say w/ millions of wearable helmets w/ video and audio as well,^[1] then what could we do with that? I'm assuming a similar pre-training stage where models are used to predict next brain-states (possibly also video and audio), and then can be finetuned or prompted for specific purposes.

Jhana helmets

Jhana is a non-addicting high pleasure state. If we can scan people entering this state, we might drastically reduce the time it takes to learn to enter this state. I predict (maybe just hope) that being able to easily enter this state will lead to an increase in psychological... (read 718 more words →)

Veo-2 Can Produce Realistic Ads

Logan Riggs

Veo-2 is google's latest video-generation model. Released Dec 16th, it's quite impressive! Of course, there are still limitations (available in that previous link), especially w/ more complex movements (e.g. skateboarder & ballerina) and consistency.

Then we have this, very realistic ad created by one person in ~3 weeks.

Most people would not be able to tell this is AI-generated (maybe 1/100k people could tell unprompted?). It is still human-edited and uses human voices. Some quick facts from the author:

How long did it take?: yup, not sure the hours. What I can backtrack is I generated 12 days for the ad, and 4 for the BTS. add editing, sound design, etc. Maybe 3 weeks?
All AI?:

... (read 188 more words →)

[Exercise] Four Examples of Noticing Confusion

Logan Riggs

Confusion is a felt sense; a bodily sensation you can pay attention to and notice! So here's my question for you:

What's this Song about?

Think About Things by Daði Frey
Youtube Link, Spotify Link
(recommended to listen to the song first, before reading the lyrics)

Lyrics

Baby I can't wait to know
Believe me I'll always be there so
Though I know I love you
I find it hard to see how you feel about me
'Cause I don't understand you
Oh you are yet to learn how to speak
When we first met
I will never forget
'Cause even though I didn't know you yet
We were bound together then and forever
And I could never let you go
Baby I can't wait to know
What do you

... (read 829 more words →)

A trending youtube video w/ 500k views in a day brings up Dario Amodei's Machines of Loving Grace (Timestamp for the quote):
[Note: I had Claude help format, but personally verified the text's faithfulness]

I am an AI optimist. I think our world will be better because of AI. One of the best expressions of that I've seen is this blog post by Dario Amodei, who is the CEO of Anthropic, one of the biggest AI companies. I would really recommend reading this - it's one of the more interesting articles and arguments I have read. He's basically saying AI is going to have an incredibly positive impact, but he's also a realist and

... (read more)

Was looking up Google Trend lines for chatGPT and noticed a cyclical pattern:

Where the dips are weekends, meaning it's mostly used by people in the workweek. I mostly expect this is students using it for homework. This is substantiated by two other trends:
1. Dips in interest over winter and summer breaks (And Thanksgiving break in above chart)

2. "Humanize AI" which is

Humanize AI™ is your go-to platform for seamlessly converting AI-generated text into authentic, undetectable, human-like content

[Although note that overall interest in ChatGPT is WAY higher than Humanize AI]

•••

Logan Riggs

Hospitalization: A Review

Seeking Power is Often Convergently Instrumental in MDPs

Sparse Autoencoders Find Highly Interpretable Directions in Language Models

A descriptive, not prescriptive, overview of current AI Alignment Research

Logan Riggs

Logan Riggs

Tensor-Transformer Variants are Surprisingly Performant

Temporarily Losing My Ego

Hospitalization: A Review

Replacing RL w/ Parameter-based Evolutionary Strategies

Telling the Difference Between Memories & Logical Guesses

Making Your Pain Worse can Get You What You Want

How to Feel More Alive

Logan Riggs

Hospitalization: A Review

Seeking Power is Often Convergently Instrumental in MDPs

Sparse Autoencoders Find Highly Interpretable Directions in Language Models

A descriptive, not prescriptive, overview of current AI Alignment Research

Logan Riggs

Logan Riggs

Tensor-Transformer Variants are Surprisingly Performant

Temporarily Losing My Ego

Hospitalization: A Review

Replacing RL w/ Parameter-based Evolutionary Strategies

Telling the Difference Between Memories & Logical Guesses

Making Your Pain Worse can Get You What You Want

How to Feel More Alive

The Architecture

Replacing MLP w/ a Bilinear Layer

Replacing Softmax Attn w/

Evolutionary Strategy (ES) Algorithm

Local Details Unique to Your Current Situation

Summary

Introduction

Stores Already Have Empty Shelves.

How do you work w/ sleep consolidation?

Implications of a Brain Scan Revolution

Jhana helmets

What's this Song about?