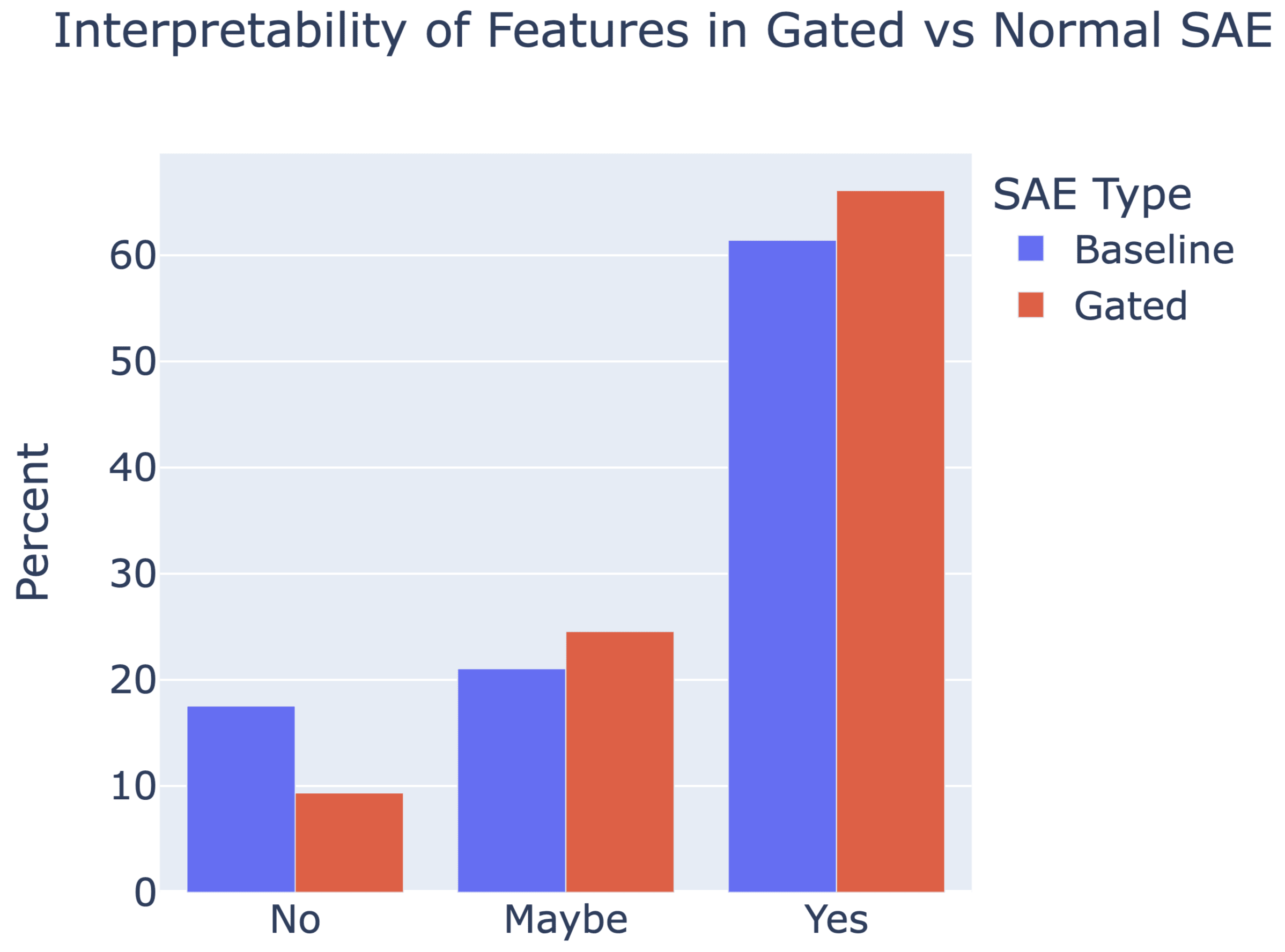
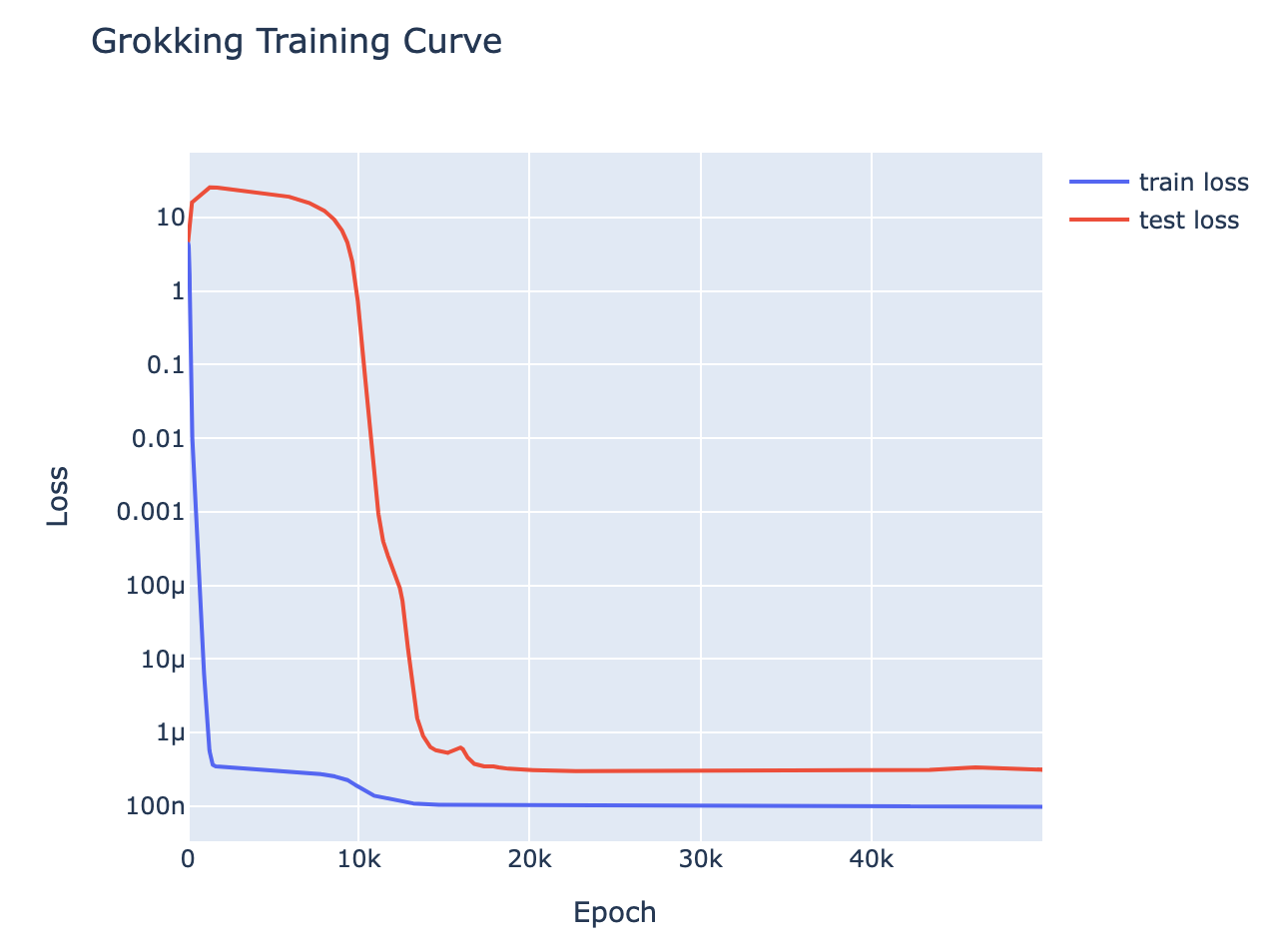
A significantly updated version of this work is now on Arxiv and was published as a spotlight paper at ICLR 2023 aka, how the best way to do modular addition is with Discrete Fourier Transforms and trig identities If you don't want to commit to a long post, check out the Tweet thread summary Introduction Grokking is a recent phenomena discovered by OpenAI researchers, that in my opinion is one of the most fascinating mysteries in deep learning. That models trained on small algorithmic tasks like modular addition will initially memorise the training data, but after a long time will suddenly learn to generalise to unseen data. A training curve for a 1L Transformer trained to do addition mod 113, trained on 30% of the 1132 pairs - it shows clear grokking This is a write-up of an independent research project I did into understanding grokking through the lens of mechanistic interpretability. My most important claim is that grokking has a deep relationship to phase changes. Phase changes, ie a sudden change in the model's performance for some capability during training, are a general phenomena that occur when training models, that have also been observed in large models trained on non-toy tasks. For example, the sudden change in a transformer's capacity to do in-context learning when it forms induction heads. In this work examine several toy settings where a model trained to solve them exhibits a phase change in test loss, regardless of how much data it is trained on. I show that if a model is trained on these limited data with high regularisation, then that the model shows grokking. Loss curve for predicting repeated subsequences in a sequence of random tokens in a 2L attention only transformer on infinite data - shows a phase changeLoss curve for predicting repeated subsequences in a sequence of random tokens in a 2L attention-only transformer given 512 training data points - shows clear grokking. One of the core claims of mechanistic interpretability is that neur