Graphical tensor notation for interpretability
[ This post is now on arXiv too: https://arxiv.org/abs/2402.01790 ] Some examples of graphical tensor notation from the QUIMB python package Deep learning consists almost entirely of operations on or between tensors, so easily understanding tensor operations is pretty important for interpretability work.[1] It's often easy to get confused about which operations are happening between tensors and lose sight of the overall structure, but graphical notation[2] makes it easier to parse things at a glance and see interesting equivalences. The first half of this post introduces the notation and applies it to some decompositions (SVD, CP, Tucker, and tensor-network decompositions), while the second half applies it to A Mathematical Framework for Transformer Circuits. Most of the first half is adapted from my physics PhD thesis introduction, which is partly based on existing explanations such as in the math3ma blog, Simon Verret's blog, tensornetwork.org, tensors.net, Hand-waving and Interpretive Dance: An Introductory Course on Tensor Networks, An Intuitive Framework for Neural Learning Systems, or a talk I gave in 2021. Feel free to scroll around and look at interesting diagrams rather than reading this post start to finish. Tensors Practically, tensors in our context can just be treated as arrays of numbers.[3] In graphical notation (first introduced by Roger Penrose in 1971), tensors are represented as shapes with "legs" sticking out of them. A vector can be represented as a shape with one leg, a matrix can be represented as a shape with two legs, and so on. I'll also represent everything in PyTorch code for clarity. Each leg corresponds to an index of the tensor - specifying an integer value for each leg of the tensor addresses a number inside of it: where 0.157 happens to be the number in the (i=0,j=2,k=0) position of the tensor A. In python, this would be A[0,2,0]. The amount of memory required to store a tensor grows exponentially with the number of legs,[4] so
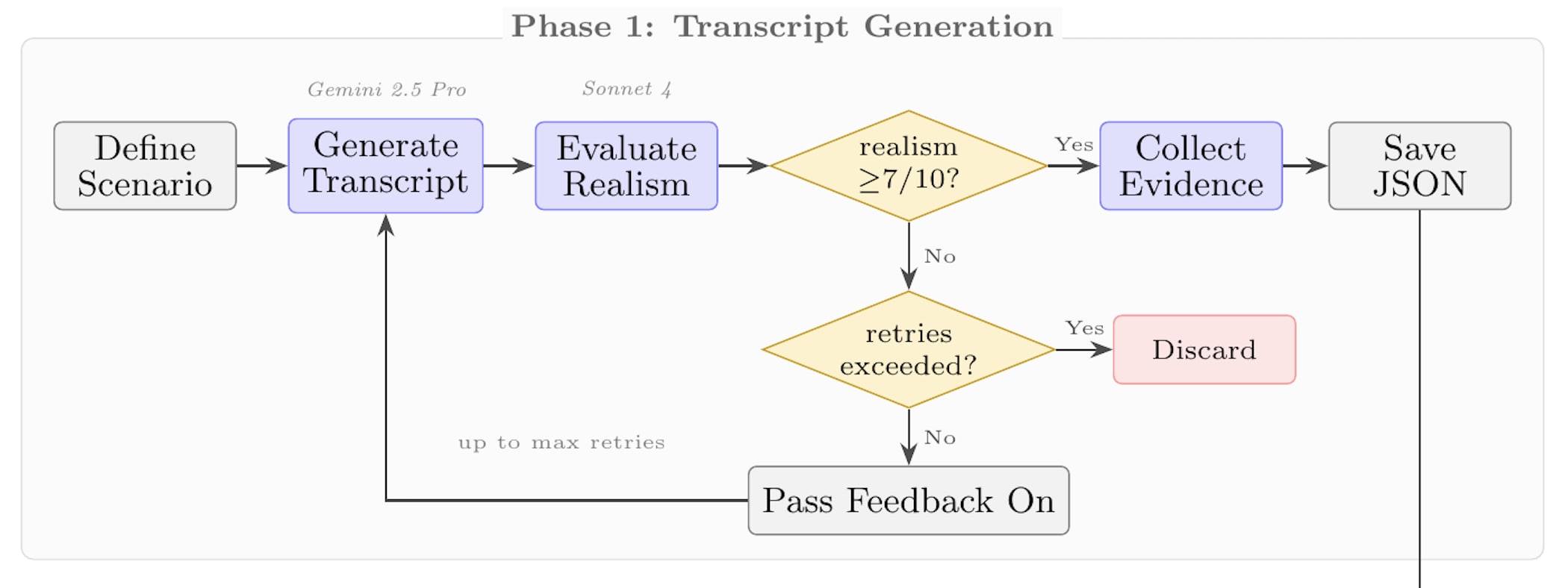

You could also make a similar eval by inserting misaligned actions into real transcripts, instead of using entirely synthetic transcripts.