LESSWRONG
LW

by So8res
11 min read
162

39

This is crossposted from my new blog. I was planning to write a short post explaining how Newcomblike problems are the norm and why any sufficiently powerful intelligence built to use causal decision theory would self-modify to stop using causal decision theory in short order. Turns out it's not such a short topic, and it's turning into a short intro to decision theory.

I've been motivating MIRI's technical agenda (decision theory and otherwise) to outsiders quite frequently recently, and I received a few comments of the form "Oh cool, I've seen lots of decision theory type stuff on LessWrong, but I hadn't understood the connection." While the intended audience of my blog is wider than the readerbase of LW (and thus, the tone might seem off and the content a bit basic), I've updated towards these posts being useful here. I also hope that some of you will correct my mistakes!

This sequence will probably run for four or five posts, during which I'll motivate the use of decision theory, the problems with the modern standard of decision theory (CDT), and some of the reasons why these problems are an FAI concern.

I'll be giving a talk on the material from this sequence at Purdue next week.

1

Choice is a crucial component of reasoning. Given a set of available actions, which action do you take? Do you go out to the movies or stay in with a book? Do you capture the bishop or fork the king? Somehow, we must reason about our options and choose the best one.

Of course, we humans don't consciously weigh all of our actions. Many of our choices are made subconsciously. (Which letter will I type next? When will I get a drink of water?) Yet even if the choices are made by subconscious heuristics, they must be made somehow.

In practice, decisions are often made on autopilot. We don't weigh every available alternative when it's time to prepare for work in the morning, we just pattern-match the situation and carry out some routine. This is a shortcut that saves time and cognitive energy. Yet, no matter how much we stick to routines, we still spend some of our time making hard choices, weighing alternatives, and predicting which available action will serve us best.

The study of how to make these sorts of decisions is known as Decision Theory. This field of research is closely intertwined with Economics, Philosophy, Mathematics, and (of course) Game Theory. It will be the subject of today's post.

2

Decisions about what action to choose necessarily involve counterfactual reasoning, in the sense that we reason about what would happen if we took actions which we (in fact) will not take.

We all have some way of performing this counterfactual reasoning. Most of us can visualize what would happen if we did something that we aren't going to do. For example, consider shouting "PUPPIES!" at the top of your lungs right now. I bet you won't do it, but I also bet that you can picture the results.

One of the major goals of decision theory is to formalize this counterfactual reasoning: if we had unlimited resources then how would we compute alternatives so as to ensure that we always pick the best possible action? This question is harder than it looks, for reasons explored below: counterfactal reasoning can encounter many pitfalls.

A second major goal of decision theory is this: human counterfactual reasoning sometimes runs afoul of those pitfalls, and a formal understanding of decision theory can help humans make better decisions. It's no coincidence that Game Theory was developed during the cold war!

(My major goal in decision theory is to understand it as part of the process of learning how to construct a machine intelligence that reliably reasons well. This provides the motivation to nitpick existing decision theories. If they're broken then we had better learn that sooner rather than later.)

3

Sometimes, it's easy to choose the best available action. You consider each action in turn, and predict the outcome, and then pick the action that leads to the best outcome. This can be difficult when accurate predictions are unavailable, but that's not the problem that we address with decision theory. The problem we address is that sometimes it is difficult to reason about what would happen if you took a given action.

For example, imagine that you know of a fortune teller who can reliably read palms to divine destinies. Most people who get a good fortune wind up happy, while most people who get a bad fortune wind up sad. It's been experimentally verified that she can use information on palms to reliably make inferences about the palm-owner's destiny.

So... should you get palm surgery to change your fate?

If you're bad at reasoning about counterfactuals, you might reason as follows:

Nine out of ten people who get a good fortune do well in life. I had better use the palm surgery to ensure a good fortune!

Now admittedly, if palm reading is shown to work, the first thing you should do is check whether you can alter destiny by altering your palms. However, assuming that changing your palm doesn't drastically affect your fate, this sort of reasoning is quite silly.

The above reasoning process conflates correlation with causal control. The above reasoner gets palm surgery because they want a good destiny. But while your palm may give information about their destiny, your palm does not control your fate.

If we find out that we've been using this sort of reasoning, we can usually do better by considering actions only on the basis of what they cause.

4

This idea leads us to causal decision theory (CDT), which demands that we consider actions based only upon the causal effects of those actions.

Actions are considered using causal counterfactual reasoning. Though causal counterfactual reasoning can be formalized in many ways, we will consider graphical models specifically. Roughly, a causal graph is a graph where the world model is divided into a series of nodes, with arrows signifying the causal connections between the nodes. For a more formal introduction, you'll need to consult a textbook. As an example, here's a causal graph for the palm-reading scenario above:

The choice is denoted by the dotted Surgery? node. Your payoff is the $ diamond. Each node is specified as a function of all nodes causing it.

For example, in a very simple deterministic version of the palm-reading scenario, the nodes could be specified as follows:

  1. Surgery? is a program implementing the agent, and must output either yes or no.
  2. Destiny is either good or bad.
  3. Fortune is always good if Surgery? is yes, and is the same as Destiny otherwise.
  4. $ is $100 if Destiny is good and $10 otherwise, minus $10 if Surgery is yes. Surgery is expensive!

Now let's say that you expect even odds on whether or not your destiny is good or bad, e.g. the probability that Destiny=good is 50%.

If the Surgery? node is a program that implements causal decision theory, then that program will choose between yes and no using the following reasoning:

  • The action node is Surgery?
  • The available actions are yes and no
  • The payoff node is $
  • Consider the action yes
    • Replace the value of Surgery? with a function that always returns yes
    • Calculate the value of $
    • We would get $90 if Destiny=good
    • We would get $0 if Destiny=bad
    • This is $45 in expectation.
  • Consider the action no
    • Replace the value of Surgery? with a function that always returns no
    • Calculate the value of $
    • We would get $100 if Destiny=good
    • We would get $10 if Destiny=bad
    • This is $55 in expectation.
  • Return no, as that yields the higher value of $.

More generally, the CDT reasoning procedure works as follows:

  1. Identify your action node A
  2. Identify your available actions Acts.
  3. Identify your payoff node U.
  4. For each action a
    • Set A to a by replacing the value of A with a function that ignores its input and returns a
    • Evaluate the expectation of U given that A=a
  5. Take the a with the highest associated expectation of U.

Notice how CDT evaluates counterfactuals by setting the value of its action node in a causal graph, and then calculating its payoff accordingly. Done correctly, this allows a reasoner to figure out the causal implications of taking a specific action without getting confused by additional variables.

CDT is the academic standard decision theory. Economics, statistics, and philosophy all assume (or, indeed, define) that rational reasoners use causal decision theory to choose between available actions.

Furthermore, narrow AI systems which consider their options using this sort of causal counterfactual reasoning are implicitly acting like they use causal decision theory.

Unfortunately, causal decision theory is broken.

5

Before we dive into the problems with CDT, let's flesh it out a bit more. Game Theorists often talk about scenarios in terms of tables that list the payoffs associated with each action. This might seem a little bit like cheating, because it often takes a lot of hard work to determine what the payoff of any given action is. However, these tables will allow us to explore some simple examples of how causal reasoning works.

I will describe a variant of the classic Prisoner's Dilemma which I refer to as the token trade. There are two players in two separate rooms, one red and one green. The red player starts with the green token, and vice versa. Each must decide (in isolation, without communication) whether or not to give their token to me, in which case I will give it to the other player.

Afterwards, they may cash their token out. The red player gets $200 for cashing out the red token and $100 for the green token, and vice versa. The payoff table looks like this:

  Give Keep
Give ( $200, $200 ) ( $0, $300 )
Keep ( $300, $0 ) ( $100, $100 )

For example, if the green player gives the red token away, and the red player keeps the green token, then the red player gets $300 while the green player gets nothing.

Now imagine a causal decision theorist facing this scenario. Their causal graph might look something like this:

Let's evaluate this using CDT. The action node is Give?, the payoff node is $. We must evaluate the expectation of $ given Give?=yes and Give?=no. This, of course, depends upon the expected value of TheirDecision.

In Game Theory, we usually assume that the opponent is reasoning using something like CDT. Then we can reason about TheirDecision given that they are doing similar reasoning about our decision and so on. This threatens to lead to infinite regress, but in fact there are some tricks you can use to guarantee at least one equilibrium. (These are the famous Nash equilibria.) This sort of reasoning requires some modifications to the simple CDT procedure given above which we're going to ignore today. Because while most scenarios with multiple agents require more complicated reasoning, the token trade is an especially simple scenario where we can brush all that under the rug.

In the token trade, the expected value of TheirDecision doesn't matter to a CDT agent. No matter what the probability p of TheirDecision=give happens to be, the CDT agent will do the following reasoning:

  • Change Give? to be a constant function returning yes
    • If TheirDecision=give then we get $200
    • If TheirDecision=keep then we get $0
    • We get 200p dollars in expectation.
  • Change Give? to be a constant function returning no
    • If TheirDecision=give then we get $300
    • If TheirDecision=keep then we get $100
    • We get 300p + 100(1-p) dollars in expectation.

Obviously, 300p+100(1-p) will be larger than 200p, no matter what probability p is.

A CDT agent in the token trade must have an expectation about TheirDecision captured by a probability p that they will give their token, and we have just shown that no matter what that p is, the CDT agent will keep their token.

When something like this occurs (where Give?=no is better regardless of the value of TheirDecision) we say that Give?=no is a "dominant strategy". CDT executes this dominant strategy, and keeps its token.

6

Of course, this means that each player will get $100, when they could have both recieved $200. This may seem unsatisfactory. Both players would agree that they could do better by trading tokens. Why don't they coordinate?

The classic response is that the token trade (better known as the Prisoner's Dilemma) is a game that explicitly disallows coordination. If players do have an opportunity to coordinate (or even if they expect to play the game mulitple times) then they can (and do!) do better than this.

I won't object much here, except to note that this answer is still unsatisfactory. CDT agents fail to cooperate on a one-shot Prisoner's Dilemma. That's a bullet that causal decision theorists willingly bite, but don't forget that it's still a bullet.

7

Failure to cooperate on the one-shot Prisoner's Dilemma is not necessarily a problem. Indeed, if you ever find yourself playing a token trade against an opponent using CDT, then you had better hold on to your token, because they surely aren't going to give you theirs.

However, CDT does fail on a very similar problem where it seems insane to fail. CDT fails at the token trade even when it knows it is playing against a perfect copy of itself.

I call this the "mirror token trade", and it works as follows: first, I clone you. Then, I make you play a token trade against yourself.

In this case, your opponent is guaranteed to pick exactly the same action that you pick. (Well, mostly: the game isn't completely symmetric. If you want to nitpick, consider that instead of playing against a copy of yourself, you must write a red/green colorblind deterministic computer program which will play against a copy of itself.)

The causal graph for this game looks like this:

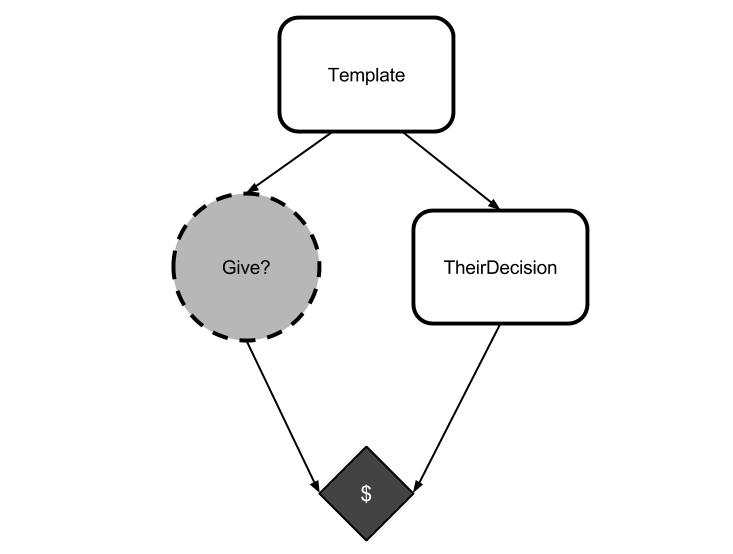
Because I've swept questions of determinism and asymmetry under the rug, both decisions will be identical. The red copy should trade its token, because that's guaranteed to get it the green token (and it's the only way to do so).

Yet CDT would have you evaluate an action by considering what happens if you replace the node Give? with a function that always returns that action. But this intervention does not affect the opponent, which reasons the same way! Just as before, a CDT agent treats TheirDecision as if it has some probability of being give that is independent from the agent's action, and reasons that "I always keep my token while they act independently" dominates "I always give my token while they act independently".

Do you see the problem here? CDT is evaluating its action by changing the value of its action node Give?, assuming that this only affects things that are caused by Give?. The agent reasons counterfactually by considering "what if Give? were a constant function that always returned yes?" while failing to note that overwriting Give? in this way neglects the fact that Give? and TheirDecision are necessarily equal.

Or, to put it another way, CDT evaluates counterfactuals assuming that all nodes uncaused by its action are independent of its action. It thinks it can change its action and only look at the downstream effects. This can break down when there are acausal connections between the nodes.

After the red agent has been created from the template, its decision no longer causally affects the decision of the green agent. But both agents will do the same thing! There is a logical connection, even though there is no causal connection. It is these logical connections that are ignored by causal counterfactual reasoning.

This is a subtle point, but an important one: the values of Give? and TheirDecision are logically connected, but CDT's method of reasoning about counterfactuals neglects this connection.

8

This is a know failure mode for causal decision theory. The mirror token trade is an example of what's known as a "Newcomblike problem".

Decision theorists occasionally dismiss Newcomblike problems as edge cases, or as scenarios specifically designed to punish agents for being "rational". I disagree.

And finally, eight sections in, I'm ready to articulate the original point: Newcomblike problems aren't a special case. They're the norm.

But this post has already run on for far too long, so that discussion will have to wait until next time.

Causal Decision Theory
Personal Blog

39

Mentioned in
Causal decision theory is unsatisfactory
-1James_Miller
14So8res
New Comment
162 comments, sorted by
top scoring
Click to highlight new comments since:
Some comments are truncated due to high volume. (⌘F to expand all)Change truncation settings
[-]Shmi150

I suspect that CDT seems not suitable for Newcomb-like problems because it tends to be applied to non-existent outcomes. If the outcome is not in the domain, you should not be calculating its utility. In the PD example CD and DC are not valid outcomes for clones. Similarly, two-boxing and getting $1001k is not a valid outcome in Newcomb. If you prune the decision tree of imaginable but non-existing branches before applying a decision theory, many differences between CDT and EDT tend to go away.

Reply
[-]lackofcheese140

Moreover, if you prune the decision tree of all branches bar one then all decision algorithms will give the same (correct) answer!

It's totally OK to add a notion of pruning in, but you can't really say that your decision algorithm of "CDT with pruning" makes sense unless you can specify which branches ought to be pruned, and which ones should not. Also, outright pruning will often not work; you may only be able to rule out a branch as highly improbable rather than altogether impossible.

In other words, "pruning" as you put it is simply the same thing as "recognizing logical connections" in the sense that So8res used in the above post.

Reply
3private_messaging
Well, a decision theory presumably is applied to some model of the physics, so that your agent can for example conclude that jumping out of a 100th floor window would result in it hitting ground at a high velocity. Finding that a hypothetical outcome is physically impossible would fall within the purview of the model of physics.
4cousin_it
As you know, I'm interested in decision theories that work in completely deterministic worlds. What does "pruning" mean if only one outcome is logically possible?
2Shmi
Not one, multiple. For example In Newcomb's you can still choose to one-box (you get $1M) or two-box (you get $1k). However, "two-box and $1001000" is not in the problem domain at all, just like killing the predictor and grabbing all its riches isn't. Similarly, if you play a game of, say, chess, there are valid moves and invalid moves. When designing a chess program you don't need to worry about an opponent making an invalid move. In the cloned PD example CD and DC are invalid moves. If an algorithm (decision theory) cannot filter them out automatically, you have to prune the list of all moves until only valid moves are left before applying it. I am surprised that this trivial observation is not completely obvious.
4cousin_it
The problem is that, for a deterministic decision algorithm running in a deterministic world, only one outcome actually happens. If you want to define a larger set of "logically possible" outcomes, I don't see a difference in principle between the outcome where your decision algorithm returns something it doesn't actually return, and the outcome where 1=2 and pumpkins fall from the sky. You might say that outcomes are "possible" or "impossible" from the agent's point of view, not absolutely. The agent must run some "pruning" algorithm, and the set of "possible" outcomes will be defined as the result of that. But then the problem is that the set of "possible" outcomes will depend on how exactly the "pruning" works, and how much time the agent spends on it. With all the stuff about self-fulfilling proofs in UDT, it might be possible to have an agent that hurts itself by overzealous "pruning".
5Shmi
I must be missing something. Suppose you write a chess program. The part of it which determines which moves are valid is separate from the part which decides which moves are good. Does a chess bot not qualify as a "deterministic decision algorithm running in a deterministic world"? Or is the issue that there is an uncertainty introduced by the other player? Then how about a Rubik cube solver? Valid moves are separate from the moves which get you close to the final state. You never apply your optimizer to invalid moves, which is exactly what CDT does in Newcomb's.
[-]James_Miller80

How will your clones play the centipede game?

Reply
[-]Anders_H60

This discussion and a previous conversation with Nate have helped me crystallize my thoughts on why I prefer CDT to any of the attempts to "fix" it using timelessness. Most of the material on TDT/UDT is too technical for me, so it is entirely possible that I am wrong; if there are errors in my reasoning, I would be very grateful if someone could point it out:

Any decision theory depends on the concept of choice: If there is no choice, there is no need for a decision theory. I have seen a quote attributed to Pearl to the effect that we can only ... (read more)

Reply
8So8res
Yeah. TDT/UDT agents don't choose their source code. They just choose their strategy. They happen to do this in a way that respects logical connections between events, whereas CDT reasons about its options in a way that neglects acausal logical connections (such as in the mirror token trade above). None of the algorithms are making different assumptions about the nature of "free will" or whether you get to "choose your own code": they differ only in how they construct their counterfactuals, with TDT/UDT respecting acausal connections that CDT neglects.
6Anders_H
I recognize that you understand this much better than me, and that I am almost certainly wrong. I am continuing this discussion only to try to figure out where my lingering sense of confusion comes from. If an agent is playing a game of PD against another agent running the same source code, and chooses to "cooperate" because he believes the that other agent will necessarily make the same choice: how is that not equivalent to choosing your source code?
4lackofcheese
It isn't equivalent. The agent recognizes that their already-existing source code is what causes them to either cooperate or defect, and so because the other agent has the same source code that agent must make the same decision. As for how the actual decision happens, the agent doesn't "choose its source code", it simply runs the source code and outputs "cooperate" or "defect" based on what the result of running that source code is.
2Anders_H
This makes sense, but if it is true, I don't understand in what sense a "choice" is made. It seems to me you have assumed away free will. Which is fine, it is probably true that free will does not exist. But if it is true, I don't understand why there is any need for a decision theory, as no decisions are actually made.
6lackofcheese
Clearly you have a notion of what it means to "make a decision". Doesn't it make sense to associate this idea of "making a decision" with the notion of evaluating the outcomes from different (sometimes counterfactual) actions and then selecting one of those actions on the basis of those evaluations? Surely if the notion of "choice" refers to anything coherent, that's what it's talking about? What matters is that the decision is determined directly through the "make a decision" process rather than independently of it. Also, given that these "make a decision" processes (i.e. decision theories) are things that actually exist and are used, surely it also makes sense to compare different decision theories on the basis of how sensibly they behave?
2Anders_H
You are probably right that I have a faulty notion of what it means to make a decision. I'll have to think about this for a few days to see if I can update...
3A1987dM
This may help you. (Well, at least it helped me -- YMMV.)
3lackofcheese
Basically, my point is that the "running the source code" part is where all of the interesting stuff actually happens, and that's where the "choice" would actually happen. It may be true that the agent "runs the source code and outputs the resulting output", but in saying that I've neglected all of the cool stuff that happens when the source code actually gets run (e.g. comparing different options, etc.). In order to establish that source code A leads to output B you would need to talk about how source code A leads to output B, and that's the interesting part! That's the part that I associate with the notion of "choice".
7tslarm
I don't think you've misunderstood; in fact I share your position. Do you also reject compatibilist accounts of free will? I think the basic point at issue here is whether or not a fully determined action can be genuinely 'chosen', any more than the past events that determine it. The set of assumptions that undermines CDT also ensures that the decision process is nothing more than the deterministic consequence (give or take some irrelevant randomness) of an earlier state of the world + physical law. The 'agent' is a fully determined cog in a causally closed system. In the same-source-code-PD, at the beginning of the decision process each agent knows that the end result will either be mutual cooperation or mutual defection, and also that the following propositions must either be all true or all false: 1. 'I was programmed to cooperate' 2. 'the other agent was programmed to cooperate' 3. 'I will cooperate' 4. 'the end result will be mutual cooperation' The agent wants Proposition 4 -- and therefore all of the other propositions -- to be true. Since all of the propositions are known to share the same truth value, choosing to make Proposition 3 true is equivalent to choosing to make all four propositions true -- including the two that refer to past events (Propositions 1 and 2). So either the agent can choose the truth value of propositions about the past, or else Proposition 3 is not really under the agent's control. I'd be interested to know whether those who disagree with me/us see a logical error above, or simply have a concept of choice/agency/free will/control that renders the previous paragraph either false or unproblematic (presumably because it allows you to single out Proposition 3 as uniquely under the agent's control, or it isn't so fussy about temporal order). If the latter, is this ultimately a semantic dispute? (I suspect that some will half-agree with that, but add that the incompatibilist notion of free will is at best empirically false and a
4[anonymous]
Decision theories are algorithms. Free will really doesn't have much to do with them. A deterministic agent must still actually use some algorithm or another to map from sensory inputs and learned knowledge to effector outputs.
3Anders_H
Thank you - this is exactly the point that I was trying to make, just stated much more articulately. I too would much appreciate responses to this, it would help me resolve some deep confusion about why very smart LessWrongers disagree with me about something important.
6IlyaShpitser
Hi, sorry, I think I misunderstood what you were unhappy with. I have not fully internalized what is happening, but my understanding (Nate please correct me if I am wrong): We can have a "causal graph" (which will include exotic causal rules, like Omega deciding based on your source code), and in this "causal graph" we have places where our source code should go, possibly in multiple places. These places have inputs and outputs, and based on these inputs and outputs we can choose any function we like from a (let's say finite for simplicity) set. We are choosing what goes into those places based on some optimality criterion. But you might ask, isn't that really weird, your own source code is what is doing the choosing, how can you be choosing it? (Is that what you mean by "incoherence due to recursion?") The proposed way out is this. What we are actually choosing is from a set of possible source codes that embeds, via quining, the entire problem and varies only in how inputs/outputs are mapped in the right places. Due to the theorem in the link it is always possible to set it up in this way. Note: the above does not contain the string "free will," I am just trying to output my incomplete understanding of how the setup is mathematically coherent. I don't think there is any "free will" in the g-formula either. ---------------------------------------- I realize the above is still not very clear (even to myself). So here is another attempt. The key idea seems to be using Kleene's theorem to reason about own source, while further having the ability to rewrite parts of own source code based on conclusions drawn. In this particular case, "choice" is defined as 1. thinking about own source code with the "causal graph" (with holes for your source code) embedded. 2. maximizing expected utility, and realizing it would be optimal if [a particular rule mapping inputs to outputs] should go into all the holes in the "causal graph" where our algorithm should go. 3. rewr
3Anders_H
Thank you - Yes, that is what I meant by recursion, and your second attempt seems to go in the right direction to answer my concerns, but I'll have to think about this for a while to see if I can be convinced. As for the G-Formula: I don't think there is free will in it either, just that in contrast with UDT/TDT, it is not inconsistent with my concept of free will. As an interesting anecdote, I am a Teaching Assistant for Jamie (who came up with the G-Formula), so I have heard him lecture on it several times now. The last couple of years he brought up experiments that seemingly provide evidence against free will and promised to discuss the implications for his theory. Unfortunately, both years he ran out of time before he got around to it. I should ask him the next time I meet him.
1IlyaShpitser
re: free will, this is one area where Jamie and Judea agree, it seems. ---------------------------------------- I think one thing I personally (and probably others) find very confusing about UDT is reconciling the picture to be consistent with temporal constraints on causality. Nothing should create physical retro causality. Here is my posited sequence of events. step 1. You are an agent with source code read/write access. You suspect there will be (in the future) Omegas in your environment, posing tricky problems. At this point (step 1), you realize you should "preprocess" your own source code in such a way as to maximize expected utility in such problems. That is, for all causal graphs (possibly with Omega causal pathways), you find where nodes for [my source code goes here] are, and you "pick the optimal treatment regime". step 2. Omega scans your source code, and puts things in boxes based on examining this code, or simulating it. step 3. Omega gives you boxes, with stuff already in them. You already preprocessed what to do, so you one box immediately and walk away with a million. Given that Omega can scan your source, and given that you can credibly rewrite own decision making source code, there is nothing exotic in this sequence of steps, in particular there is no retro causality anywhere. It is just that there are some constraints (what people here call "logical counterfactuals") that force the output of Omega's sim at step 2, and your output at step 3 to coincide. This constraint is what lead you to preprocess to one box in step 1, by drawing an "exotic causal graph" with Omega's sim creating an additional causal link that seemingly violates "no retro causality." ---------------------------------------- The "decision" is in step 1. Had you counterfactually decided to not preprocess there, or preprocess to something else, you would walk away poorer in step 3. There is this element to UDT of "preprocessing decisions in advance." It seems all real choi
1nshepperd
This is closer to describing the self-modifying CDT approach. One of the motivations for development of TDT and UDT is that you don't necessarily get an opportunity to do such self-modification beforehand, let alone to compute the optimal decisions for all possible scenarios you think might occur. So the idea of UDT is that the design of the code should already suffice to guarantee that if you end up in a newcomblike situation you behave "as if" you did have the opportunity to do whatever precommitment would have been useful. When prompted for a decision, UDT asks "what is the (fixed) optimal conditional strategy" and outputs the result of applying that strategy to its current state of knowledge. Basically this, except there's no need to actually do it beforehand. If you like, you can consider the UDT agent's code itself to be the output of such "preprocessing"... except that there is no real pre-computation required, apart from giving the UDT agent a realistic prior.
1dankane
Actually, no. To implement things correctly, UDT needs to determine its entire strategy all at once. It cannot decide whether to one-box or two-box in Newcomb just by considering the Newcomb that it is currently dealing with. It must also consider all possible hypothetical scenarios where any other agent's action depends on whether or not UDT one-boxes. Furthermore, UDT cannot decide what it does in Newcomb independently of what it does in the Counterfactual Mugging, because some hypothetical entity might give it rewards based on some combination of the two behaviors. UDT needs to compute its entire strategy (i.e. it's response to all possible scenarios) all at the same time before it can determine what it should do in any particular situation [OK. Not quite true. It might be able to prove that whatever the optimal strategy is it involves doing X in situation Y without actually determining the optimal strategy. Then again, this seems really hard since doing almost anything directly from Kolmogorov priors is basically impossible].
1nshepperd
Conceptually, yes. The point is that you don't need to actually literally explicitly compute your entire strategy at t=-∞. All you have to do is prove a particular property of the strategy (namely, its action in situation Y) at the time when you are asked for a decision. Obviously, like every computational activity ever, you must still make approximations, because it is usually infeasible to make inferences over the entire tegmark-IV multiverse when you need to make a decision. An example of such approximations would be neglecting the measure of "entities that give it rewards based on some combination of [newcomb's and counterfactual mugging]" in many situations because I expect such things to be rare (significantly rarer than newcomb's and counterfactual mugging themselves).
0IlyaShpitser
Consider the set of all possible source codes an agent might have. This set is partitioned in two: those on which Omega rewards you (where you both one box, and your source code is such that Omega can tell you will), and those on which Omega punishes you (all others). Call the former set A, and the latter set B. Agents are not guaranteed to start with a source code in set A, some start with source code in B. (Maybe they are classically trained causal decision theorists? Maybe they are skeptical about UDT? Maybe their programmers were careless? Who knows!) The point is, there comes a time in an agent's life when it needs to grow up and move its source code to set A. Maybe it does not immediately self-modify to directly do UDTish things on Newcomb-like causal graphs, maybe it self-modifies to self-modify before being asked to one box. But it is crucial for the agent to move itself from set B to set A at some point before Omega shows up. This is what I mean by step 1.
1Anders_H
I think what confuses me is that if we want the logical connections to hold (between my decision and the decision of another agent running the same source code), it is necessary that when he preprocesses his source code he will deterministically make the same choice as me. Which means that my decision about how to preprocess has already been made by some deeper part of my source code
3IlyaShpitser
My understanding of the statement of Newcomb is that Omega puts things on boxes only based on what your source code says you will do when faced with input that looks like the Newcomb's problem. Since the agent already preprocessed the source code (possibly using other complicated bits of its own source code) to one box on Newcomb, Omega will populate boxes based on that. Omega does not need to deal with any other part of the agent's source code, including some unspecified complicated part that dealt with preprocessing and rewriting, except to prove to itself that one boxing will happen. All that matters is that the code currently has the property that IF it sees the Newcomb input, THEN it will one box. ---------------------------------------- Omega that examines the agent's code before the agent preprocessed will also put a million dollars in, if it can prove the agent will self-modify to one-box before choosing the box.
1Jiro
Phrasing it in terms of source code makes it more obvious that this is equivalent to expecting Omega to be able to solve the halting problem.
1IlyaShpitser
This is fighting the hypothetical, Omega can say it will only put a million in if it can find a proof of you one boxing quickly enough.
1Jiro
If Omega only puts the million in if it finds a proof fast enough, it is then possible that you will one-box and not get the million. (And saying "there isn't any such Omega" may be fighting the hypothetical. Saying there can't in principle be such an Omega is not.)
2nshepperd
Yes, it's possible, and serves you right for trying to be clever. Solving the halting problem isn't actually hard for a large class of programs, including the usual case for an agent in a typical decision problem (ie. those that in fact do halt quickly enough to make an actual decision about the boxes in less than a day). If you try to deliberately write a very hard to predict program, then of course omega takes away the money in retaliation, just like the other attempts to "trick" omega by acting randomly or looking inside the boxes with xrays.
-3Jiro
The problem requires that Omega be always able to figure out what you do. If Omega can only figure out what you can do under a limited set of circumstances, you've changed one of the fundamental constraints of the problem. You seem to be thinking of this as "the only time someone won't come to a decision fast enough is if they deliberately stall", which is sort of the reverse of fighting the hypothetical--you're deciding that an objection can't apply because the objection applies to an unlikely situation. Suppose that in order to decide what to do, I simulate Omega in my head as one of the steps of the process? That is not intentionally delaying, but it still could result in halting problem considerations. Or do you just say that Omega doesn't give me the money if I try to simulate him?
0[anonymous]
Usually, in the thought experiment, we assume that Omega has enough computation power to simulate the agent, but that the agent does not have enough computation power to compute Omega. We usually further assume that the agent halts and that Omega is a perfect predictor. However, these are expositional simplifications, and none of these assumptions are necessary in order to put the agent into a Newcomblike scenario. For example, in the game nshepperd is describing (where Omega plays Newcomb's problem, but only puts the money in the box if it has very high confidence that you will one-box) then, if you try to simulate Omega, you won't get the money. You're still welcome to simulate Omega, but while you're doing that, I'll be walking away with a million dollars and you'll be spending lots of money on computing resources. No one's saying you can't, they're just saying that if you find yourself in a situation where someone is predicting you and rewarding you for obviously acting like they want you to, and you know this, then it behooves you to obviously act like they want you to. Or to put it another way, consider a game where Omega is only a pretty good predictor who only puts the money in the box if Omega predicts that you one-box unconditionally (e.g. without using a source of randomness) and whose predictions are correct 99% of the time. Omega here doesn't have any perfect knowledge, and we're not necessarily assuming that anyone has superpowers, but i'd still onebox. Or if you want to see a more realistic problem (where the predictor has only human-level accuracy) then check out Hintze's formulation of Parfit's Hitchhiker (though be warned, I'm pretty sure he's wrong about TDT succeeding on this formulation of Parfit's Hitchhiker. UDT succeeds on this problem, but TDT would fail.)
1dankane
I think some that favor CDT would claim that you are are phrasing the counterfactual incorrectly. You are phrasing the situation as "you are playing against a copy of yourself" rather than "you are playing against an agent running code X (which just happens to be the same as yours) and thinks you are also running code X". If X=CDT, then TDT and CDT each achieve the result DD. If X=TDT, then TDT achieves CC, but CDT achieves DC. In other words TDT does beat CDT in the self matchup. But one could argue that self matchup against TDT and self matchup against CDT are different scenarios, and thus should not be compared.
4IlyaShpitser
I think UDT is fine (but I think it needs a good intro paper, maybe something with graphs in it...) For the kinds of problems you and I think about, UDT just reduces to CDT, e.g. it should pick the "optimal treatment regime," e.g. it is not unsound. So as far as we are concerned, there is no conflict at all. However, there is a set of (what you and I would call) "weird" problems where if you "represent the weirdness" properly and do the natural thing to pick the best treatment, UDT is what happens. One way to phrase the weirdness that happens in Newcomb is that "conditional ignorability" fails. That is, Omega introduces a new causal pathway by which your decision algorithm may affect the outcome. (Note that you might think that "conditional ignorability" also fails in e.g. the front-door case which is still a "classical problem," but actually there is a way to think about the front door case as applying conditional ignorability twice.) Since CDT is phrased on "classical" DAGs and (as the SWIG paper points out) it's all just graphical ways of representing ignorability (what they call modularity and factorization), it cannot really talk about Newcomb type cases properly. ---------------------------------------- I am not sure I understood the OP though, when he said that Newcomb problems are "the norm." Classical decision problems seem to be the norm to me.
8So8res
Yeah, it's a bold claim :-) I haven't made any of the arguments yet, but I'm getting there. (The rough version is that Newcomblike problems happen whenever knowledge about your decision theory leaks to other agents, and that this happens all the time in humans. Evolution has developed complex signaling tools, humans instinctively make split-second assessments of the trustworthiness of others, etc. In most real-world multi-agent scenarios, we implicitly expect that the other agents have some knowledge of how we make decisions, even if that's only a via knowledge of shared humanity. Any AI interacting with humans who have knowledge of its source code, even tangentially, faces similar difficulties. You could assume away the implications of this "leaked" knowledge, or artificially design scenarios in which this knowledge is unavailable. This is often quite useful as a simplifying assumption or a computational expedient, but it requires extra assumptions or extra work. By default, real-world decision problems on Earth are Newcomblike. Still a rough argument, I know, I'm working on filling it out and turning it into posts.)
1cousin_it
I prefer to argue that many real-world problems are AMD-like, because there's a nonzero chance of returning to the same mental state later, and that chance has a nonzero dependence on what you choose now. To the extent that's true, CDT is not applicable and you really need UDT, or at least this simplified version. That argument works even if the universe contains only one agent, as long as that agent has finite memory :-)
1IlyaShpitser
I think it might be helpful to be more precise about problem classes, e.g. what does "Newcomb-like" mean?. That is, the kinds of things that I can see informally arising in settings humans deal with (lots of agents running around) also contain things like blackmail problems, which UDT does not handle. So it is not really fair to say this class is "Newcomb-like," if by that class we mean "problems UDT handles properly."
3So8res
Thanks, I think you're right. (For reference, I'll be defining "Newcomblike" roughly as "other agents have knowledge of your decision algorithm". You're correct that this includes problems where UDT performs poorly, and that UDT is by no means the One Final Answer. In fact, I'm not planning to discuss UDT at all in this sequence; my goal is to motivate the idea that we don't know enough about decision theory yet to be comfortable constructing a system capable of undergoing an intelligence explosion. The fact that Newcomblike problems are fairly common in the real world is one facet of that motivation.)
1[anonymous]
What problems does UDT fail on? Why would a self-improving agent not improve its own decision-theory to reach an optimum without human intervention, given a "comfortable" utility function in the first place?
4pengvado
A self-improving agent does improve its own decision theory, but it uses its current decision theory to predict which self-modifications would be improvements, and broken decision theories can be wrong about that. Not all starting points converge to the same answer.
2[anonymous]
Oh. Oh dear. DERP. Of course: the decision theory of sound self-improvement is a special case of the decision theory for dealing with other agents.
-1dankane
I disagree. CDT correctly solves all problems in which other agents cannot read your mind. Real world occurrences of mind reading are actually uncommon.
[-]King Ali10

This account of decision theory/game theory seems like unnecessary formalism. The single play-through token problem prisoners dilemma has 4 outcomes to consider and between those 4 outcomes, no matter what your opponent does, your outcome is better if you betray so you betray.

The difference with the mirror token problem is that you set it up so that there are explicitly only two outcomes to consider. you betray and get 100 dollars or you cooperate and get 200 dollars. Obviously you choose the one that has the higher expected value os you get 200 dollars. ... (read more)

Reply
2TurnTrout
Your solution hardcodes logical influence as causal influence; these are quite different. Suppose your twin is a light-year away from you. Are you saying that your choice now exerts a causal influence over an event which is space-like separated from you?  You sound like you're saying "you're choosing what kind of agent you want (both agents) to be"; in that case, you're looking at something more akin to Functional Decision Theory.
[-]nshepperd10

Note that both CDT and EDT have the different problem that they fail on the Transparent Newcomb's problem, due to updating on their observations. This is sort of the converse problem to the one described in the post - falsely eliminating seemingly impossible outcomes that are actually reachable depending on your strategy.

Reply
[-]Error10

Yet CDT would have you evaluate an action by considering what happens if you replace the node Give? with a function that always returns that action. But this intervention does not affect the opponent, which reasons the same way!

This doesn't seem obvious to me. It looks to me like the graph is faulty; there should be "TheirDecision" and "YourDecision" nodes, each successors of the Give? node, such that changing the Give? node causally affects both. The Give? node is a function; the decision nodes are its outputs. With the graph structured like that, you get sane behavior.

Reply
4lackofcheese
The notion of how to correctly construct that causal graph is, in itself, part of the decision theory. CDT constructs a faulty graph because CDT itself explicitly states that you control the "YourDecision" nodes, and that those nodes should be treated as having no predecessors.
[-]dankane00

Yes. I agree that CDT fails to achieve optimal results in circumstances where the program that you are running directly affects the outside universe. For example, in clone PD, where running a program causes the opponent to run the same program, or in Newcomb's problem, where running a program that 2-boxes causes the second box to be empty. On the other hand, ANY decision theory can be made to fail in such circumstances. You could merely face a universe that determines whether you are running program X and charges you $100 if you are.

Are there circumstances where the universe does not read your mind where CDT fails?

Reply
[-][anonymous]100

Are there circumstances where the universe does not read your mind where CDT fails?

I'm sure we could think of some, but I want to address the question of "universe reads your mind". Social agents (ie: real, live people) reason about each-other's minds all the time. There is absolutely nothing weird or unusual about this, and there really oughtn't be anything weird about trying to formalize how it ought be done.

Reply
-1dankane
OK. Name one.
3[anonymous]
Correlation-by-congruent-logic can show up in situations that don't necessarily have to do with minds, particularly the agent's mind, but the agent needs to either have an epistemology capable of noticing the correlations and equating them logically within its decision-making procedure -- TDT reaches in that direction.
0dankane
Sorry. I'm not quite sure what you're saying here. Though, I did ask for a specific example, which I am pretty sure is not contained here. Though to clarify, by "reading your mind" I refer to any situation in which the scenario you face (including the given description of that scenario) depends directly on which program you are running and not merely upon what that program outputs.
-1dankane
There's a difference between reasoning about your mind and actually reading your mind. CDT certainly faces situations in which it is advantageous to convince others that it does not follow CDT. On the other hand, this is simply behaving in a way that leads to the desired outcome. This is different from facing situations where you can only convince people of this by actually self-modifying. Those situations only occur when other people can actually read your mind.
2A1987dM
Humans are not perfect deceivers.
1dankane
I suppose. On the other hand, is that because other people can read your mind or because you have emotional responses that you cannot suppress and are correlated to what you are thinking? This is actually critical to what counterfactuals you want to construct. Consider for example the terrorist who would try to bring down an airplane that he is on given the opportunity. Unfortunately, he's an open book and airport security would figure out that he's up to something and prevent him from flying. This is actually inconvenient since it also means he can't use air travel. He would like to be able to precommit to not trying to take down particular flights so that he would be allowed on. On the other hand, whether or not this would work depends on what exactly airport security is picking up on. Are they actually able to discern his intent to cause harm, or are they merely picking up on his nervousness at being questioned by airport security. If it's the latter, would an internal precommitment to not bring down a particular flight actually solve his problem? Put another way, is the TSA detecting the fact that the terrorist would down the plane if given the opportunity, or simply that he would like to do so (in the sense of getting extra utils from doing so).
[-]itaibn0-10

On this topic, I'd like to suggest a variant of Newcomb's problem that I don't recall seeing anywhere in LessWrong (or anywhere else). As usual, Omega presents you with two boxes, box A and box B. She says "You may take either box A or both boxes. Box B contains 1,000$. Box A either contains 1,000,000$ or is empty. Here is how I decided what to put in box A: I consider a perfectly rational agent being put in an identical situation to the one you're in. If I predict she takes one box I put the money in box A, otherwise I put nothing." Suppose furt... (read more)

Reply
1hairyfigment
Didn't we just cover this? If not, I don't understand what Omega's saying here.
-1dankane
I think even TDT says that you should 2-box in Newcomb's problem when the box is full if and only if false. But more seriously, presumably in your scenario the behavior of a "perfectly rational agent" actually means the behavior of an agent whose behavior is specified by some fixed, known program. In this case, the participant can determine whether or not the box is full. Thus, either the box is always full or the box is always empty, and the participant knows which is the case. If you are playing Newcomb's problem with the box always full, you 2-box. If you play Newcomb's problem with the box always empty, you 2-box. Therefore you 2-box. Therefore, the perfectly rational agent 2-boxes. Therefore, the box is always empty. OK. OK. OK. You TDT people will say something like "but I am a perfectly rational agent and therefore my actions are non-causally related to whether or not the box is full, thus I should 1-box as it will cause the box to be full." On the other hand, if I modify your code to 2-box in this type of Newcomb's problem you do better and thus you were never perfectly rational to begin with. On the other hand, if the universe can punish you directly (i.e. not simply via your behavior) for running the wrong program, the program that does best depends heavily on which universe you are in and thus there cannot be a "perfectly rational agent" unless you assume a fixed prior over possible universes.
[-]V_V-10

CDT is the academic standard decision theory. Economics, statistics, and philosophy all assume (or, indeed, define) that rational reasoners use causal decision theory to choose between available actions.

Reference?

I'm under the impression that Expected (Von Neumann–Morgenstern) Utility Maximization, aka Evidential Decision Theory is generally considered the ideal theory, while CDT was originally considered as an approximation used to make the computation tractable.
In 1981 Gibbard, Harper and Lewis started to argue that CDT was superior to Expected Utilit... (read more)

Reply
5IlyaShpitser
You need to do more reading. CDT is basically what all of statistics, econometrics, etc. standardized on now (admittedly under a different name of 'potential outcomes'), since at least the 70s. There is no single reference, since it's a huge area, but start with "Rubin-Neyman causal model." Many do not agree with Pearl on various points, but almost everyone uses potential outcomes as a starting point, and from there CDT falls right out. The subfield of causal graphical models started with Wright's path analysis papers in the 1920s, by the way. ---------------------------------------- edit: Changed Neyman to Wright, I somehow managed to get them confused :(.
1V_V
This looks like an approach to model inference given the data, while CDT, in the sense the OP is talking about, is an approach to decision making given the model.
9IlyaShpitser
I mean this in the nicest possible way, but please understand that if you try to google for five minutes, you are going to be outputting nonsense on this topic (and indeed lots of topics). Seriously, do some reading: this stuff is not simple.
1Anders_H
I think it is unfortunate that the word "Decision Theory" is used for both VNM and CDT. These are not in the same reference class and are not inconsistent with each other. I think the distinction between CDT and EDT is orthogonal to whether we represent the utilities of the outcomes with a VNM utility function. CDT says we should make our choice based on the distribution of outcomes if we intervene such that a is chosen. This is in contrast to EDT, which allows you to choose based on the distribution of outcomes in people who were historically observed to choose a. EDT is subject to confounding, therefore quite clearly, Gibbard, Harper and Lewis were correct to argue that CDT is superior to EDT. This is accepted in all academic fields, it is very reasonable to claim that CDT is the standard academic decision theory. CDT tells you to compare your beliefs about the distribution of Y| do(a) to Y| do(a') whereas EDT tells you to compare your beliefs about the distribution of Y|a to Y|a'. Note that neither CDT nor EDT specify how to evaluate which distribution of outcomes is better. This is what you need VNM for. You could in principle use VNM for either, but I find it obvious that Von Neumann and Morgenstern were implicitly assuming a Causal Decision Theory.
[-]James_Miller-10

However, CDT does fail on a very similar problem where it seems insane to fail. CDT fails at the token trade even when it knows it is playing against a perfect copy of itself.

I don't see this as a failure. As I'm sure you know, if the game still is a PD then regardless of what my clone does I'm still always better off defecting. If either my actions influence what my clone does, or I care about my clone's wealth then the game might no longer be a PD and as simple game theory would predict I might not defect.

Reply
[-]So8res140

Imagine the following game: You give me a program that must either output "give" or "keep". I play it in a token trade (as defined above) against itself. I give you the money from only the first instance (you don't get the wealth that goes to the second instance).

Would you be willing to pay me $150 to play this game? (I'd be happy to pay you $150 to give me this opportunity, for the same reason that I cooperate with myself on a one-shot PD.)

regardless of what my clone does I'm still always better off defecting.

This is broken counterfactual reasoning. It assumes that your action is independent of your clone's just because your action does not influence your clone's. According to the definition of the game, the clone will happen to defect if you defect and will happen to cooperate if you cooperate. If you respect this logical dependence when constructing your counterfactuals, you'll realize that reasoning like "regardless of what my clone does I..." neglects the fact that you can't defect while your clone cooperates.

Reply
3lackofcheese
The "give me a program" game carries the right intuition, but keep in mind that a CDT agent will happily play it and win it because they will naturally view the decision of "which program do I write" as the decision node and consequently get the right answer. The game is not quite the same as a one-shot PD, at the least because CDT gives the right answer.
9So8res
Right! :-D This is precisely one of the points that I'm going to make in an upcoming post. CDT acts differently when it's in the scenario compared to when ask it to choose the program that will face the scenario. This is what we mean by "reflective instability", and this is what we're alluding to when we say things like "a sufficiently intelligent self-modifying system using CDT to make decisions would self-modify to stop using CDT to make decisions". (This point will be expanded upon in upcoming posts.)
3lackofcheese
That's exactly what I was thinking as I wrote my post, but I decided not to bring it up. Your later posts should be interesting, although I don't think I need any convincing here---I already count myself as part of the "we" as far as the concepts you bring up are concerned.
2dankane
OK. I'll bite. What's so important about reflective stability? You always alter your program when you come across new data. Now sure we usually think about this in terms of running the same program on a different data set, but there's no fundamental program/data distinction. The acting differently when choosing a program and being in the scenario is perhaps worrying, but I think that it's intrinsic to the situation we are in when your outcomes are allowed to depend on the behavior of counterfactual copies of you. For example, consider the following pair of games. In REWARD, you are offered $1000. You can choose whether or not to accept. That's it. In PUNISHMENT, you are penalized $1000000 if you accepted the money in REWARD. Thus programs win PUNISHMENT if and only if they lose REWARD. If you want to write a program to play one it will necessarily differ from the program you would write to play the other. In fact the program playing PUNISHMENT will behave differently than the program you would have written to play the (admittedly counterfactual) subgame of REWARD. How is this any worse than what CDT does with PD?
5So8res
Nothing in particular. There is no strong notion of dominance among decision theories, as you've noticed. The problem with CDT isn't that it's unstable under reflection, it's that it's unstable under reflection in such a way that it converges on a bad solution that is much more stable. That point will take a few more posts to get to, but I do hope to get there.
1dankane
I guess I'll see your later posts then, but I'm not quite sure how this could be the case. If self-modifying-CDT is considering making a self modification that will lead to a bad solution, it seems like it should realize this and instead not make that modification.
4So8res
Indeed. I'm not sure I can present the argument briefly, but a simple analogy might help: a CDT agent would pay to precommit to onebox before playing Newcomb's game, but upon finding itself in Newcomb's game without precommitting, it would twobox. It might curse its fate and feel remorse that the time for precommitment had passed, but it would still twobox. For analogous reasons, a CDT agent would self-modify to do well on all Newcomblike problems that it would face in the future (e.g., it would precommit generally), but it would not self-modify to do well in Newcomblike games that were begun in its past (it wouldn't self-modify to retrocommit for the same reason that CDT can't retrocommit in Newcomb's problem: it might curse its fate, but it would still perform poorly). Anyone who can credibly claim to have knowledge of the agent's original decision algorithm (e.g. a copy of the original source) can put the agent into such a situation, and in certain exotic cases this can be used to "blackmail" the agent in such a way that, even if it expects the scenario to happen, it still fails (for the same reason that CDT twoboxes even though it would precommit to oneboxing). [Short story idea: humans scramble to get a copy of a rouge AI's original source so that they can instantiate a Newcomblike scenario that began in the past, with the goal of regaining control before the AI completes an intelligence explosion.] (I know this is not a strong argument yet; the full version will require a few more posts as background. Also, this is not an argument from "omg blackmail" but rather an argument from "if you start from a bad starting place then you might not end up somewhere satisfactory, and CDT doesn't seem to end up somewhere satisfactory".)
2dankane
I am not convinced that this is the case. A self-modifying CDT agent is not caused to self-modify in favor of precommitment by facing a scenario in which precommitment would have been useful, but instead by evidence that such scenarios will occur in the future (and in fact will occur with greater frequency than scenarios that punish you for such precommitments). Actually, this seems like a bigger problem with UDT to me than with SMCDT (self-modifying CDT). Either type of program can be punished for being instantiated with the wrong code, but only UDT can be blackmailed into behaving differently by putting it in a Newcomb-like situation. The story idea you had wouldn't work. Against a SMCDT agent, all that getting the AIs original code would allow people to do is to laugh at it for having been instantiated with code that is punished by the scenario they are putting it in. You manipulate a SMCDT agent by threatening to get ahold of its future code and punishing it for not having self-modified. On the other hand, against a UDT agent you could do stuff. You just have to tell it "we're going to simulate you and if the simulation behaves poorly, we will punish the real you". This causes the actual instantiation to change its behavior if it's a UDT agent but not if it's a CDT agent. On the other hand, all reasonable self-modifying agents are subject to blackmail. You just have to tell them "every day that you are not running code with property X, I will charge you $1000000".
3one_forward
Can you give an example where an agent with a complete and correct understanding of its situation would do better with CDT than with UDT? An agent does worse by giving in to blackmail only if that makes it more likely to be blackmailed. If a UDT agent knows opponents only blackmail agents that pay up, it won't give in. If you tell a CDT agent "we're going to simulate you and if the simulation behaves poorly, we will punish the real you," it will ignore that and be punished. If the punishment is sufficiently harsh, the UDT agent that changed its behavior does better than the CDT agent. If the punishment is insufficiently harsh, the UDT agent won't change its behavior. The only examples I've thought of where CDT does better involve the agent having incorrect beliefs. Things like an agent thinking it faces Newcomb's problem when in fact Omega always puts money in both boxes.
2dankane
Well, if the universe cannot read your source code, both agents are identical and provably optimal. If the universe can read your source code, there are easy scenarios where one or the other does better. For example, "Here have $1000 if you are a CDT agent" Or "Here have $1000 if you are a UDT agent"
2one_forward
Ok, that example does fit my conditions. What if the universe cannot read your source code, but can simulate you? That is, the universe can predict your choices but it does not know what algorithm produces those choices. This is sufficient for the universe to pose Newcomb's problem, so the two agents are not identical. The UDT agent can always do at least as well as the CDT agent by making the same choices as a CDT would. It will only give a different output if that would lead to a better result.
4dankane
Actually, here's a better counter-example, one that actually exemplifies some of the claims of CDT optimality. Suppose that the universe consists of a bunch of agents (who do not know each others' identities) playing one-off PDs against each other. Now 99% of these agents are UDT agents and 1% are CDT agents. The CDT agents defect for the standard reason. The UDT agents reason that my opponent will do the same thing that I do with 99% probability, therefore, I should cooperate. CDT agents get 99% DC and 1% DD. UDT agents get 99% CC and 1% CD. The CDT agents in this universe do better than the UDT agents, yet they are facing a perfectly symmetrical scenario with no mind reading involved.
2Wei Dai
A version of this problem was discussed here previously. It was also brought up during the decision theory workshop hosted by MIRI in 2013 as an open problem. As far as I know there hasn't been much progress on it since 2009.
0private_messaging
I wonder if it's even coherent to have a math intuition which wouldn't be forcing UDT to cooperate (or defect) in certain conditions just to make 2*2 be 4 , figuratively speaking (as ultimately you could expand any calculation into an equivalent calculation involving a decision by UDT).
2nshepperd
That shouldn't be surprising. The CDT agents here are equivalent to DefectBot, and if they come into existence spontaneously, are no different than natural phenomena like rocks. Notice that the UDT agents in this situation do better than the alternative (if they defected, they would get 100% DD which is a way worse result). They don't care that some DefectBots get to freeload. Of course, if the defectbots are here because someone calculated that UDT agents would cooperate and therefore being defectbot is a good way to get free utilons... then the UDT agents are incentivized to defect, because this is now an ultimatum game. And in the variant where bots do know each other's identities, the UDT bots all get 99% CC / 1% DD and the CDT bots suck it.
3dankane
And the UDT agents are equivalent to CooperateBot. What's your point?
2dankane
The CDT agents here win because they do not believe that altering their strategy will change the way that their opponents behave. This is actually true in this case, and even true for the UDT agents depending on how you choose to construct your counterfactuals. If a UDT agent suffered a malfunction and defected, it too would do better. In any case, the theorem that UDT agents perform optimally in universes that can only read your mind by knowing what you would do in hypothetical situations is false as this example shows. UDT bots win in some scenarios where the initial conditions of the scenario favor agents that behave sub-optimally in certain scenarios (and by sub-optimally, I mean where counterfactuals are constructed in the way implicit to CDT). The example above shows that sometimes they are punished for acting suboptimally.
1dankane
Or how about this example, that simplifies things even further. The game is PD against CooperateBot, BUT before the game starts Omega announces "your opponent will make the same decision that UDT would if I told them this." This announcement causes UDT to cooperate against CooperateBot. CDT on the other hand, correctly deduces that the opponent will cooperate no matter what it does (actually UDT comes to this conclusion too) and therefore decides to defect.
2nshepperd
No. There is no obligation to do something just because Omega claims that you will. First, if I know that my opponent is CooperateBot, then:- 1. It is known that Omega doesn't lie. 2. Therefore Omega has simulated this situation and predicted that I (UDT) cooperate. 3. Hence, I can either cooperate, and collect the standard reward for CC. 4. Or I can defect, in order to access an alternative branch of the problem (where Omega finds that UDT defects and does "something else"). 5. This alternative branch is unspecified, so the problem is incomplete. UDT cooperates or defects depending on the contents of the alternative branch. If the alternative branch is unknown then it must guess, and most likely cooperates to be on the safe side. Now, the problem is different if a CDT agent is put in my place, because that CDT agent does not control (or only weakly controls) the action of the UDT simulation that Omega ran in order to make the assertion about UDT's decision.
1dankane
Fine. Your opponent actually simulates what UDT would do if Omega had told it that and returns the appropriate response (i.e. it is CooperateBot, although perhaps your finite prover is unable to verify that).
2nshepperd
Err, that's not CooperateBot, that's UDT. Yes, UDT cooperates with itself. That's the point. (Notice that if UDT defects here, the outcome is DD.)
1dankane
It's not UDT. It's the strategy that against any opponent does what UDT would do against it. In particular, it cooperates against any opponent. Therefore it is CooperateBot. It is just coded in a funny way. To be clear letting Y(X) be what Y does against X we have that BOT(X) = UDT(BOT) = C This is different from UDT. UDT(X) is D for some values of X. The two functions agree when X=UDT and in relatively few other cases.
3lackofcheese
What is your point, exactly? It's clear that UDT can't do better vs "BOT" than by cooperating, because if UDT defects against BOT then BOT defects against UDT. Given that dependency, you clearly can't call it CooperateBot, and it's clear that UDT makes the right decision by cooperating with it because CC is better than DD.
1dankane
OK. Let me say this another way that involves more equations. So let's let U(X,Y) be the utility that X gets when it plays prisoner's dilemma against Y. For a program X, let BOT^X be the program where BOT^X(Y) = X(BOT^X). Notice that BOT^X(Y) does not depend on Y. Therefore, depending upon what X is BOT^X is either equivalent CooperateBot or equivalent to DefectBot. Now, you are claiming that UDT plays optimally against BOT_UDT because for any strategy X U(X, BOT^X) <= U(UDT, BOT^UDT) This is true, because X(BOT^X) = BOT^X(X) by the definition of BOT^X. Therefore you cannot do better than CC. On the other hand, it is also true that for any X and any Y that U(X,BOT^Y) <= U(CDT, BOT^Y) This is because BOT^Y's behavior does not depend on X, and therefore you do optimally by defecting against it (or you could just apply the Theorem that says that CDT wins if the universe cannot read your mind). Our disagreement here stems from the fact that we are considering different counterfactuals here. You seem to claim that UDT behaves correctly because U(UDT,BOT^UDT) > U(CDT,BOT^CDT) While I claim that CDT does because U(CDT, BOT^UDT) > U(UDT, BOT^UDT) And in fact, given the way that I phrased the scenario, (which was that you play BOT^UDT not that you play BOT^{you} (i.e. the mirror matchup)) I happen to be right here. So justify it however you like, but UDT does lose this scenario.
2lackofcheese
Actually, you've oversimplified and missed something critical. In reality, the only way you can force BOT^UDT(X) = UDT(BOT^UDT) = C is if the universe does, in fact, read your mind. In general, UDT can map different epistemic states to different actions, so as long as BOT^UDT has no clue about the epistemic state of the UDT agent it has no way of guaranteeing that its output is the same as that of the UDT agent. Consequently, it's possible for the UDT agent to get DC as well. The only way BOT^UDT would be able to guarantee that it gets the same output as a particular UDT agent is if the universe was able to read the UDT agent's mind.
0dankane
Actually, I think that you are misunderstanding me. UDT's current epistemic state (at the start of the game) is encoded into BOT^UDT. No mind reading involved. Just a coincidence. [Really, your current epistemic state is part of your program] Your argument is like saying that UDT usually gets $1001000 in Newcomb's problem because whether or not the box was full depended on whether or not UDT one-boxed when in a different epistemic state.
2nshepperd
Okay, you're saying here that BOT has a perfect copy of the UDT player's mind in its own code (otherwise how could it calculate UDT(BOT) and guarantee that the output is the same?). It's hard to see how this doesn't count as "reading your mind". Yes, sometimes its advantageous to not control the output of computations in the environment. In this case UDT is worse off because it is forced to control both its own decision and BOT's decision; whereas CDT doesn't have to worry about controlling BOT because they use different algorithms. But this isn't due to any intrinsic advantage of CDT's algorithm. It's just because they happen to be numerically inequivalent. An instance of UDT with literally any other epistemic state than the one contained in BOT would do just as well as CDT here.
1dankane
So... UDT's source code is some mathematical constant, say 1893463. It turns out that UDT does worse against BOT^1893463. Note that it does worse against BOT^1893463 not BOT^{you}. The universe does not depend on the source code of the person playing the game (as it does in mirror PD). Furthermore, UDT does not control the output of its environment. BOT^1893463 always cooperates. It cooperates against UDT. It cooperates against CDT. It cooperates everything. No. CDT does at least as well as UDT against BOT^CDT. UDT does worse when there is this numerical equivalence, but CDT does not suffer from this issue. CDT does at least as well as UDT against BOT^X for all X, and sometimes does better. In fact, if you only construct counterfactuals this way, CDT does at least as well as anything else. This is silly. A UDT that believes that it is in a mirror matchup also loses. A UDT that believes it is facing Newcomb's problem does something incoherent. If you are claiming that you want a UDT that differs from the encoding in BOT because, of some irrelevant details in its memory... well then it might depend upon implementation, but I think that most attempted implementations of UDT would conclude that these irrelevant details are irrelevant and cooperate anyway. If you don't believe this then you should also think that UDT will defect in a mirror matchup if it and its clone are painted different colors.
4nshepperd
I take it back, the scenario isn't that weird. But your argument doesn't prove what you think it does: Consider the analogous scenario, where CDT plays against BOT = CDT(BOT). CDT clearly does the wrong thing here - it defects. If it cooperated, it would get CC instead of DD. Note that if CDT did cooperate, UDT would be able to freeload by defecting (against BOT = CDT(BOT)). But CDT doesn't care about that because the prisoner's dilemma is defined such that we don't care about freeloaders. Nevertheless CDT defects and gets a worse result than it could. CDT does better than UDT against BOT = UDT(BOT) because UDT (correctly) doesn't care that CDT can freeload, and correctly cooperates to gain CC. Depending on the exact setup, "irrelevant details in memory" are actually vital information that allow you to distinguish whether you are "actually playing" or are being simulated in BOT's mind.
0dankane
No. BOT^CDT = DefectBot. It defects against any opponent. CDT could not cause it to cooperate by changing what it does. Actually if CDT cooperated against BOT^CDT it would get $3^^^3. You can prove all sorts of wonderful things once you assume a statement that is false. OK... So UDT^Red and UDT^Blue are two instantiations of UDT that differ only in irrelevant details. In fact the scenario is a mirror matchup, only after instantiation one of the copies was painted red and the other was painted blue. According to what you seem to be saying UDT^Red will reason: Well I can map different epistemic states to different outputs, I can implement the strategy cooperate if you are painted blue and defect if you are painted red. Of course UDT^Blue will reason the same way and they will fail to cooperate with each other.
3hairyfigment
Maybe I've misread you, but this sounds like an assertion that your counterfactual question is the right one by definition, rather than a meaningful objection.
0dankane
Well, yes. Then again, the game was specified as PD against BOT^CDT not as PD against BOT^{you}. It seems pretty clear that for X not equal to CDT that it is not the case that X could achieve the result CC in this game. Are you saying that it is reasonable to say that CDT could achieve a result that no other strategy could just because it's code happens to appear in the opponent's program? I think that there is perhaps a distinction to be made between things that happen to be simulating your code and this that are causally simulating your code.
0nshepperd
No, because that's a silly thing to do in this scenario. For one thing, UDT will see that they are reasoning the same way (because they are selfish and only consider "my color" vs "other color"), and therefore will both do the same thing. But also, depending on the setup, UDT^Red's prior should give equal probability to being painted red and painted blue anyway, which means trying to make the outcome favour red is silly. Compare to the version of newcomb's where the bot in the room is UDT^Red, while Omega simulates UDT^Blue. UDT can implement the conditional strategy {Red => two-box, Blue => one-box}. This is obviously unlikely, because the point of the Newcomb thought experiment is that Omega simulates (or predicts) you. So he would clearly try to avoid adding such information that "gives the game away". However in this scenario you say that BOT simulates UDT "by coincidence", not by mind reading. So it is far more likely that BOT simulates (the equivalent) of UDT^Blue, while the UDT actually playing is UDT^Red. And you are passed the code of BOT as input, so UDT can simply implement the conditional strategy {cooperate iff the color inside BOT is the same as my color}.
0dankane
OK. Fine. Point taken. There is a simple fix though. MBOT^X(Y) = X'(MBOT^X) where X' is X but with randomized irrelevant experiences. In order to produce this properly, MBOT only needs to have your prior (or a sufficiently similar probability distribution) over irrelevant experiences hardcoded. And while your actual experiences might be complicated and hard to predict, your priors are not.
1dankane
No. BOT(X) is cooperate for all X. It behaves in exactly the same way that CooperateBot does, it just runs different though equivalent code. And my point was that CDT does better against BOT than UDT does. I was asked for an example where CDT does better than UDT where the universe cannot read your mind except via through your actions in counterfactuals. This is an example of such. In fact, in this example, the universe doesn't read your mind at all. Also your argument that UDT cannot possibly do better against BOT than it does in analogous to the argument that CDT cannot do better in the mirror matchup than it does. Namely that CDT's outcome against CDT is at least as good as anything else's outcome against CDT. You aren't defining your counterfactuals correctly. You can do better against BOT than UDT does. You just have to not be UDT.
2dankane
Actually, this is a somewhat general phenomenon. Consider for example, the version of Newcomb's problem where the box is full "if and only if UDT one-boxes in this scenario". UDT's optimality theorem requires the in the counterfactual where it is replaced by a different decision theory that all of the "you"'s referenced in the scenario remain "you" rather than "UDT". In the latter counterfactual CDT provably wins. The fact that UDT wins these scenarios is an artifact of how you are constructing your scenarios.
1one_forward
This is a good example. Thank you. A population of 100% CDT, though, would get 100% DD, which is terrible. It's a point in UDT's favor that "everyone running UDT" leads to a better outcome for everyone than "everyone running CDT."
2dankane
Fine. How about this: "Have $1000 if you would have two-boxed in Newcomb's problem."
4nshepperd
The optimal solution to that naturally depend on the relative probabilities of that deal being offered vs newcomb's itself.
2dankane
OK. Fine. I will grant you this: UDT is provably optimal if it has correct priors over possible universes and the universe can read its mind only through determining its behavior in hypothetical situations (because UDT basically is just find the behavior pattern that optimizes expected utility and implement that). On the other hand, SMCDT is provably optimal in situations where it has an accurate posterior probability distribution, and where the universe can read its mind but not its initial state (because it just instantly self-modifies to the optimally performing program). I don't see why the former set of restrictions is any more reasonable than the latter, and at least for SMCDT you can figure out what it would do in a given situation without first specifying a prior over possible universes. I'm also not convinced that it is even worth spending so much effort trying to decide the optimal decision theory in situations where the universe can read your mind. This is not a realistic model to begin with.
1dankane
Actually, I take it back. Depending on how you define things, UDT can still lose. Consider the following game: I will clone you. One of the clones I paint red and the other I paint blue. The red clone I give $1000000 and the blue clone I fine $1000000. UDT clearly gets expectation 0 out of this. SMCDT however can replace its code with the following: If you are painted blue: wipe your hard drive If you are painted red: change your code back to standard SMCDT Thus, SMCDT never actually has to play blue in this game, while UDT does.
2one_forward
You seem to be comparing SMCDT to a UDT agent that can't self-modify (or commit suicide). The self-modifying part is the only reason SMCDT wins here. The ability to self-modify is clearly beneficial (if you have correct beliefs and act first), but it seems separate from the question of which decision theory to use.
2dankane
Which is actually one of the annoying things about UDT. Your strategy cannot depend simply on your posterior probability distribution, it has to depend on your prior probability distribution. How you even in practice determine your priors for Newcomb vs. anti-Newcomb is really beyond me. But in any case, assuming that one is more common, UDT does lose this game.
2nshepperd
No-one said that winning was easy. This problem isn't specific to UDT. It's just that CDT sweeps the problem under the rug by "setting its priors to a delta function" at the point where it gets to decide. CDT can win this scenario if it self-modifies beforehand (knowing the correct frequencies of newcomb vs anti-newcomb, to know how to self-modify) - but SMCDT is not a panacea, simply because you don't necessarily get a chance to self-modify beforehand.
1dankane
CDT does not avoid this issue by "setting its priors to the delta function". CDT deals with this issue by being a theory where your course of action only depends on your posterior distribution. You can base your actions only on what the universe actually looks like rather than having to pay attention to all possible universes. Given that it's basically impossible to determine anything about what Kolmogorov priors actually say, being able to totally ignore parts of probability space that you have ruled out is a big deal. ... And this whole issue with not being able to self-modify beforehand. This only matters if your initial code affects the rest of the universe. To be more precise, this is only an issue if the problem is phrased in such a way that the universe you have to deal with depends on the code you are running. If we instantiate the Newcomb's problem in the middle of the decision, UDT faces a world with the first box full while CDT faces a world with the first box empty. UDT wins because the scenario is in its favor before you even start the game. If you really think that this is a big deal, you should try to figure out which decision theories are only created by universes that want to be nice to them and try using one of those.
2dankane
Actually thinking about it this way, I have seen the light. CDT makes the faulty assumption that your initial state in uncorrelated with the universe that you find yourself in (who knows, you might wake up in the middle of Newcomb's problem and find that whether or not you get $1000000 depends on whether or not your code is such that you would one-box in Newcomb's problem). UDT goes some ways to correct this issue, but it doesn't go far enough. I would like to propose a new, more optimal decision theory. Call it ADT for Anthropic Decision Theory. Actually, it depends on a prior, so assume that you've picked out one of those. Given your prior, ADT is the decision theory D that maximizes the expected (given your prior) lifetime utility of all agents using D as their decision theory. Note how agents using ADT do provably better than agents using any other decision theory. Note that I have absolutely no idea what ADT does in, well, any situation, but that shouldn't stop you from adopting it. It is optimal after all.
2one_forward
Why does UDT lose this game? If it knows anti-Newcomb is much more likely, it will two-box on Newcomb and do just as well as CDT. If Newcomb is more common, UDT one-boxes and does better than CDT.
2dankane
I guess my point is that it is nonsensical to ask "what does UDT do in situation X" without also specifying the prior over possible universes that this particular UDT is using. Given that this is the case, what exactly do you mean by "losing game X"?
2nshepperd
Well, you can talk about "what does decision theory W do in situation X" without specifying the likelyhood of other situations, by assuming that all agents start with a prior that sets P(X) = 1. In that case UDT clearly wins the anti-newcomb scenario because it knows that actual newcomb's "never happens" and therefore it (counterfactually) two-boxes. The only problem with this treatment is that in real life P(anti-newcomb) = 1 is an unrealistic model of the world, and you really should have a prior for P(anti-newcomb) vs P(newcomb). A decision theory that solves the restricted problem is not necessarily a good one for solving real life problems in general.
2dankane
Well, perhaps. I think that the bigger problem is that under reasonable priors P(Newcomb) and P(anti-Newcomb) are both so incredibly small that I would have trouble finding a meaningful way to approximate their ratio. How confident are you that UDT actually one-boxes? Also yeah, if you want a better scenario where UDT loses see my PD against 99% prob. UDT and 1% prob. CDT example.
2nshepperd
Only if the adversary makes its decision to attempt extortion regardless of the probability of success. In the usual case, the winning move is to ignore extortion, thereby retroactively making extortion pointless and preventing it from happening in the first place. (Which is of course a strategy unavailable to CDT, who always gives in to one-shot extortion.)
1dankane
And thereby the extortioner's optimal strategy is to extort independently of the probably of success. Actually, this is probably true is a lot of real cases (say ransomware) where the extortioner cannot actually ascertain the probably of success ahead of time.
2pengvado
That strategy is optimal if and only if the probably of success was reasonably high after all. Otoh, if you put an unconditional extortioner in an environment mostly populated by decision theories that refuse extortion, then the extortioner will start a war and end up on the losing side.
1dankane
Yes. And likewise if you put an unconditional extortion-refuser in an environment populated by unconditional extortionists.
1hairyfigment
I think this is actually the point (though I do not consider myself an expert here). Eliezer thinks his TDT will refuse to give in to blackmail, because outputting another answer would encourage other rational agents to blackmail it. By contrast, CDT can see that such refusal would be useful in the future, so it will adopt (if it can) a new decision theory that refuses blackmail and therefore prevents future blackmail (causally). But if you've already committed to charging it money, its self-changes will have no causal effect on you, so we might expect Modified CDT to have an exception for events we set in motion before the change.
1dankane
This just means that TDT loses in honest one-off blackmail situations (in reality, you don't give in to blackmail because it will cause other people to blackmail you whether or not you then self-modify to never give into blackmail again). TDT only does better if the potential blackmailers read your code in order to decide whether or not blackmail will be effective (and then only if your priors say that such blackmailers are more likely than anti-blackmailers who give you money if they think you would have given into blackmail). Then again, if the blackmailers think that you might be a TDT agent, they just need to precommit to using blackmail whether or not they believe that it will be effective. Actually, this suggests that blackmail is a game that TDT agents really lose badly at when playing against each other. The TDT blackmailer will decide to blackmail regardless of effectiveness and the TDT blackmailee will decide to ignore the blackmail, thus ending in the worst possible outcome.
2Shmi
Assume it's not a perfect clone, it can defect with probability p even if you cooperate. Then apply CDT. You get "defect" for any p>0. So it is reasonable to implicitly assume continuity and declare that CDT forces you to defect when p=0. However, if you apply CDT for the case p=0 directly, you get "cooperate" instead. In other words, the conterfactual reasoning gets broken when the map CDT(p, PD) is not continuous at the point p=0.
5So8res
I disagree. If the agent has a 95% probability of doing the same thing as me and a 5% chance of defecting, I still cooperate. (With 95% probability, most likely, because you gotta punish defectors.) Indeed, consider the following game: You give me a program that must either output "give" or "keep". I roll a 20 sided die. On a 20, I play your program against a program that always keeps its token. Otherwise, I play your program against itself. I give you the money that (the first instance of) your program wins. Are you willing to pay me $110 to play? I'd be happy to pay you $110 for this opportunity. I don't cooperate with myself because P(TheirChoice=Defect)=0, I cooperate with myself because I don't reason as if p is independent from my action.
4lackofcheese
It's not entirely clear what you're saying, but I'll try to take the simplest interpretation. I'm guessing that: * If you're going to defect, your clone always defects. * If you're going to cooperate, your clone cooperates with probability 1-p and defects with probability p In that case, I don't see how it is that you get "defect" for p>0; the above formulation gives "cooperate" for 0<=p<0.5.
1A1987dM
Suppose you have to submit the source code of a program X, and I will play Y = “run X, then do what X did with probability 0.99 and the reverse with probability 0.01” against Y' which is the same as Y but with a different seed for the RNG, and pay you according to how Y does. Then “you” (i.e. Y) are not a perfect clone of your opponent (i.e. Y'). What do you do?
0James_Miller
You have to consider off-the-equilibrium-path behavior. If I'm the type of person who will always cooperate, what would happen if I went off-the-equilibrium-path and did defect even if my defecting is a zero probability event?
4Shmi
I'm trying to understand the difference between your statement and "1 is not equal 2, but what if it were?" and failing.
1solipsist
See trembling hand equilibrium.
1Shmi
Right, as I mentioned in my other reply, CDT is discontinuous at p=0. Presumably a better decision theory would not have such a discontinuity.
1Jiro
One possible interpretation of "if I always cooperate, what would happen if I don't" is "what is the limit, as X approaches 1, of 'if I cooperate with probability X, what would happen if I don't'?" This doesn't reasonably map onto the 1=2 example.
1Shmi
Right. There seems to be a discontinuity, as the limit of CDT (p->0) is not CDT (p=0). I wonder if this is the root of the issue.
1James_Miller
"1 is not equal 2, but what if it were?" = what if I could travel faster than the speed of light. Off the equilibrium path = what if I were to burn a dollar. Or things I can't do vs things I don't want to do.
1Shmi
In my mind "I'm the type of person who will always cooperate" means that there is no difference between the two in this case. Maybe you use a different definition of "always"?
1James_Miller
I always cooperate because doing so maximizes my utility since it is better than all the alternatives. I always go slower than the speed of light because I have no alternatives.
1Adele_L
You can consider it, but conditioned on the information that you are playing against your clone, you should assign this a very low probability of happening, and weight it in your decision accordingly.
-3James_Miller
Assume I am the type of person who would always cooperate with my clone. If I asked myself the following question "If I defected would my payoff be higher or lower than if I cooperated even though I know I will always cooperate" what would be the answer?
3VAuroch
The answer would be 'MOO'. Or 'Mu', or 'moot'; they're equivalent. "In this impossible counterfactual where I am self-contradictory, what would happen?"
3lackofcheese
Yes, it makes a little bit of sense to counterfactually reason that you would get $1000 more if you defected, but that is predicated on the assumption that you always cooperate. You cannot actually get that free $1000 because the underlying assumption of the counterfactual would be violated if you actually defected.
1VAuroch
No, you don't. This is a game where there are only two possible outcomes; DD and CC. CD and DC are defined to be impossible because the agents playing the game are physically incapable of making those outcomes occur. EDIT: Maybe physically incapable is a bit strong. If they wanted to maximize the chance that they had unmatched outcomes, they could each flip a coin and take C if heads and D if tails, and would have a 50% chance of unmatching. But they still would both be playing the same precise strategy.
-1James_Miller
I don't agree. Even if I'm certain I will not defect, I am capable of asking what would happen if I did, just as the real me both knows he won't do "horrible thing" yet can mentally model what would happen if he did "horrible thing". Or imagine an AI that's programmed to always maximize its utility. This AI still could calculate what would happen if it followed a non-utility maximizing strategy. Often in game theory a solution requires you to calculate your payoff if you left the equilibrium path.
1VAuroch
Yes, and part of the answer is "If I did defect, my clone would also defect." You have a guarantee that both of you take the same actions because you think according to precisely identical reasoning.
1James_Miller
What do you think will happen if clones play the centipede game?
3VAuroch
Unclear, depends on the specific properties of the person being cloned. Unlike PD, the two players aren't in the same situation, so they can't necessarily rely on their logic being the same as their counterpart. How closely this would reflect the TDT ideal of 'Always Push' will depend on how luminous the person is; if they can model what they would do in the opposite situation, and are highly confident that their self-model is correct, they can reach the best result, but if they lack confidence that they know what they'd do, then the winning cooperation is harder to achieve. Of course, if it's denominated in money and is 100 steps of doubling, as implied by the Wikipedia page, then the difference in utility between $1 nonillion and $316 octillion is so negligible that there's essentially no incentive to defect in the last round and any halfway-reasonable person will Always Push straight through the game. But that's a degenerate case and probably not the version originally discussed.
1pragmatist
What would you say about the following decision problem (formulated by Andy Egan, I believe)? You have a strong desire that all psychopaths in the world die. However, your desire to stay alive is stronger, so if you yourself are a psychopath you don't want all psychopaths to die. You are pretty sure, but not certain, that you're not a psychopath. You're presented with a button, which, if pressed, would kill all psychopaths instantly. You are absolutely certain that only a psychopath would press this button. Should you press the button or not? It seems to me the answer is "Obviously not", precisely because the "off-path" possibility that you're a non-psychopath who pushes the button should not enter into your consideration. But the causal decision algorithm would recommend pushing the button if your prior that you are a psychopath is small enough. Would you agree with that?
4Jiro
If only a psychopath would push the button, then your possible non-psychopathic nature limits what decision algorithms you are capable of following.
1helltank
Wouldn't the fact that you're even considering pushing the button(because if only a psychopath would push the button then it follows that a non-psychopath would never push the button) indicate that you are a psychopath and therefore you should not push the button? Another way to put it is: If you are a psychopath and you push the button, you die. If you are not a psychopath and you push the button, pushing the button would make you a psychopath(since only a psychopath would push), and therefore you die.
2pragmatist
Pushing the button can't make you a psychopath. You're either already a psychopath or you're not. If you're not, you will not push the button, although you might consider pushing it.
1helltank
Maybe I was unclear. I'm arguing that the button will never, ever be pushed. If you are NOT a psychopath, you won't push, end of story. If you ARE A psychopath, you can choose to push or not push. In all three cases the correct decision is not to push, therefore you should not push.
1lackofcheese
Shouldn't you also update your belief towards being a psychopath on the basis that you have a strong desire that all psychopaths in the world die?
1pragmatist
You can stipulate this out of the example. Let's say pretty much everyone has the desire that all psychopaths die, but only psychopaths would actually follow through with it.
1James_Miller
I don't press. CDT fails here because (I think) it doesn't allow you to update your beliefs based on your own actions.
3crazy88
Exactly what information CDT allows you to update your beliefs on is a matter for some debate. You might be interested in a paper by James Joyce (http://www-personal.umich.edu/~jjoyce/papers/rscdt.pdf) on the issue (which was written in response to Egan's paper).
1pragmatist
But then shouldn't you also update your beliefs about what your clone will do based on your own actions in the clone PD case? Your action is very strong (perfect, by stipulation) evidence for his action.
1James_Miller
Yes I should. In the psychopath case whether I press the button depends on my beliefs, in contrast in a PD I should defect regardless of my beliefs.
1pragmatist
Maybe I misunderstand what you mean by "updating beliefs based on action". Here's how I interpret it in the psychopath button case: When calculating the expected utility of pushing the button, don't use the prior probability that you're a psychopath in the calculation, use the probability that you're a psychopath conditional on deciding to push the button (which is 1). If you use that conditional probability, then the expected utility of pushing the button is guaranteed to be negative, no matter what the prior probability that you're a psychopath is. Similarly, when calculating the expected utility of not pushing the button, use the probability that you're a psychopath conditional on deciding not to push the button. But then, applying the same logic to the PD case, you should calculate expected utilities for your actions using probabilities for your clone's action that are conditional on the very action that you are considering. So when you're calculating the expected utility for cooperating, use probabilities for your clone's action conditional on you cooperating (i.e., 1 for the clone cooperating, 0 for the clone defecting). When calculating the expected utility for defecting, use probabilities for your clone's action conditional on you defecting (0 for cooperating, 1 for defecting). If you do things this way, then cooperating ends up having a higher expected utility. Perhaps another way of putting it is that once you know the clone's actions are perfectly correlated with your own, you have no good reason to treat the clone as an independent agent in your analysis. The standard tools of game theory, designed to deal with cases involving multiple independent agents, are no longer relevant. Instead, treat the clone as if he were part of the world-state in a standard single-agent decision problem, except this is a part of the world-state about which your actions give you information (kind of like whether or not you're a psychopath in the button case).
1James_Miller
I agree with your first paragraph. Imagine you are absolutely certain you will cooperate and that your clone will cooperate. You are still capable of asking "what would my payoff be if I didn't cooperate" and this payoff will be the payoff if you defect and the clone cooperates since you expect the clone to do whatever you will do and you expect to cooperate. There is no reason to update my belief on what the clone will do in this thought experiment since the thought experiment is about a zero probability event. The psychopath case is different because I have uncertainty regarding whether I am a psychopath and the choice I want to make helps me learn about myself. I have no uncertainty concerning my clone.
1VAuroch
You are reasoning about an impossible scenario; if the probability of you reaching the event is 0, the probability of your clone reaching it is also 0. In order to make it a sensical notion, you have to consider it as epsilon probabilities; since the probability will be the same for both your and your clone, this gets you %5E2%20+%20300%20\epsilon%20\cdot%20(1-\epsilon)%20+%20100%20\epsilon%5E2%20=%20200%20-%20400\epsilon%20+%20200\epsilon%5E2%20+%20300\epsilon%20-300%20\epsilon%5E2%20+%20100%20\epsilon%5E2%20=%20200%20-100\epsilon), which is maximized when . To claim that you and your clone could take different actions is trying to make it a question about trembling-hand equilibria, which violates the basic assumptions of the game.
1James_Miller
It's common in game theory to consider off the equilibrium path situations that will occur with probability zero without taking a trembling hand approach.
0[anonymous]
I don't think you use use "always" correctly.
Moderation Log
162Comments