As an initial aside, I wonder if there is a general factor of spherical-cow-trustingness (SCT?) which separates us. I surely have a moderate amount of SCT! This is not a stance which is easily succinctly justified, but for me comes from having seen (and conjured) many successful spherical cows over the years. Have you read MacKay's Information Theory, Inference, and Learning Algorithms? In the chapter 'Why have sex?', he has an even more spherical model of natural selection than mine here, which I (and many others) consider very illuminating. But, it's so spherical. So spherical. Still works :).

On that note, my models here of evolution seem pretty solid and obviously capturing the spirit, to me. The first one (which I call 'annealing-style') is very close to a classic introduction of simulated annealing, a widely-used/considered simple mutate-and-select algorithm. The second one is less rigorously-presented but captures a lot more of the spirit and detail of natural evolutions, including horizontal transfer and a larger population.

This is a much appreciated critique. You've clearly engaged with this post in some depth and put effort in to describe some disagreements. I'm not currently moved (beyond the existing stance of the original post, which has a bunch of caveats and future work).

On to some specific responses.

[Of the first evolution model:] the true fitness function is not an expectation value which we could noisily estimate with sampling

No, I think it just is this, the sampling being the stochastic realisation of competition between differently-fit individuals/populations/alleles. If you wanted, you could introduce something like a 'data distribution' (e.g. of environmental scenarios) and an expectation over success-rates on that distribution as the true-loss analogue. But you'd just end up with something of the form of my i.e. there'd be some latent 'true fitness' or 'true Elo-across-envs' (the actual expectation) and sample-based estimation would yield some (locally monotonic) probability of an 'actually fitter' instance being measured as such in any given lineup.^[1]

a prescribed stochastic relationship ( $P_{s}$ ) between the true gradient and the next step.

Mild push-back (I'm not sure exactly what you're trying to say here): I don't prescribe a relationship between the gradient and the next step. All I prescribe is that fitter instances are directionally selected/preferred. The gradient comes out of the maths; that's basically the heart of this post!

Your example of correlated directions is really nice. I agree that SGD in full generality can have this. I also think a less spherical model of mutation+selection would also have this! (In fact lots of empirical and theoretical genetics finds/predicts correlations.)

Go back to my 'distribution of environment scenarios' lower-level model. Certainly this could induce correlations if we wanted it to, for basically the same reasons as in your example.

On descendant-generation and population, I refer at first to my spherical-cow-trustingness. To me it obviously captures the spirit! But in any case, I think the details are closer than you seem to allow.

Here, there is always exactly one descendant.

This is only true of one semantic, for the first model. The first model also has another, population-wise semantic. 'Instead of a parent individual and cloned and mutated offspring individuals, considering parent and offspring populations, the same reasoning and proof is immediately applicable if we assume that mutations arise sufficiently rarely to be either fixed or lost before the next mutation arises... Of course this is not true for real natural selection.'

In the second model there is a population of different individuals with different genomes, consisting of a 'fixed' part and a set of 'in flight' (not yet fixed or extinct) mutations. This is a less-spherical cow, but I think captures even more the detail and spirit of real natural selection.

On learning rates, I appreciate this remark. I called this out in the original as something for further research, but (for SCT reasons) I don't consider it especially important/urgent.

(S)GD does not have a gradient-dependent learning rate. To call this an equivalence, I'd want to know the conditions under which the learning rate is constant (if this is possible).

As I said elsewhere, any number of practical departures from pure SGD mess with the step size anyway (and with the gradient!) so this feels like asking for too much. Do we really think SGD vs momentum vs Adam vs ... is relevant to the conclusions we want to draw? (Serious question; my best guess is 'no', but I hold that medium-lightly.)

Now think about the space including SGD, RMSProp, etc. The 'depends on gradient norm' piece which arises from my evolution model seems entirely at home in that family. But I would also be interested in further analysis exploring the details of (various models of) natural selection from a 'learning rate' POV.

Of course, in practical SGD, there are also often learning-rate schedules, including decay but also more wacky things. Would be interesting (but not especially loadbearing) to learn more about how natural selection handles this (I've heard it suggested that mutation-rate, among other things, is meta-selected for adaptability, which seems eminently plausible).

This post calls $f$ the "fitness function," which is not (AFAIK) how the term "fitness" is used evolutionary biology.

True, usually. But in Darwin's day, 'fitness' just meant 'how fitted are you to the environment?' i.e. 'what's your Elo rating here?', which has later been operationalised in various ways, usually accounting for number or proportion of descendants (either at a genetic unit level or at an inclusive genetic level for organisms).

We might care about the quantity whose gradient we're ascending, or about the biology-fitness, but $f$ is not either of those.

$f$ is the quantity whose gradient we're ascending. And it's biology-fitness in the pre-operationalisation-as-fecundity/offspring sense.

Please let me know if I've missed anything that seems important to you - these are longish comments.

e.g. imagine characterising the sample-based loss estimate via mean and variance. For now, assume normal and homoscedastic (more spherical cows!). Is my claim about a monotonic selection prob arising from this then basically clear? There's some prob of 'accidentally' getting samples which invert the fitness order, but this prob decreases as the true fitness difference increases. (For non-normal or heteroscedastic, this still holds locally, but the coefficients will be different in different regions.) ↩︎

See in context

70 Conditions for mathematical equivalence of Stochastic Gradient Descent and Natural Selection

by Oliver Sourbut

9th May 2022

AI Alignment ForumLinkpost from www.oliversourbut.net

9 min read

70 Ω 27

Many thanks to Peter Barnett, my alpha interlocutor for the first version of the proof presented, and draft reader.

Analogies are often drawn between natural selection and gradient descent (and other training procedures for parametric algorithms). It is important to understand to what extent these are useful and applicable analogies.

Here, under some modest (but ultimately approximating) simplifying assumptions, natural selection is found to be mathematically equivalent to an implementation of stochastic gradient descent.

The simplifying assumptions are presented first, followed by a proof of equivalence. Finally, a first attempt is made to consider the effect of relaxing each of these assumptions and what departure it causes from the equivalence, and an alternative set of assumptions which retrieves a similar equivalence is presented.

Summary of simplifying assumptions

It is essential to understand that the equivalence rests on some simplifying assumptions, none of which is wholly true in real natural selection.

Fixed 'fitness function' or objective function mapping genome to continuous 'fitness score'
Continuous fixed-dimensional genome
Radially symmetric mutation probability density
Limit case to infinitesimal mutation
A degenerate population of 1 or 2
No recombination or horizontal transfer

(NB assumptions 5 and 6 will be addressed in detail and amended later)

Proof

Setup and assumptions

Let us make some substantial modelling simplifications, while retaining the spirit of natural selection, to yield an 'annealing style' selection process.

We have continuous genome with fixed fitness/objective function $f : R^{n} \to R$

Mutations are distributed according to probability density $P_{m} : R^{n} \to [0, 1]$ which is radially symmetric

so $\forall ϵ \in R^{n} . P_{m} (ϵ) = g (| ϵ |)$ for some $g : R^{+} \to [0, 1]$ (a density, but not a probability density)
a mutation in one direction is just as likely as a mutation in another direction

We also consider the case of mutations very small relative to the genome, tending to infinitesimal.

Selection is stochastic, but monotonically determined by the fitness differential, according to selection function $P_{s} : R \to [0, 1]$

so the probability of $x^{'}$ being selected over $x$ is $P_{s} (f (x^{'}) - f (x))$
$P_{s}$ is a monotonically nondecreasing function: a greater 'fitness score' differential can not reduce chances of selection
- i.e. $\forall Δ, δ \in R . Δ > δ ⟹ P_{s} (Δ) \geq P_{s} (δ)$
a good model for this is something like a softmax, Boltzmann, or logistic function^[1], i.e. a normalised ratio of exponentials, but this is not essential for the proof

The population alternates between a single parent and its two offspring, one of which is selected to become the next generation's parent.

selection according to $P_{s}$ abstracts any mechanism which results in becoming the ancestor of future generations
- not dying first
- reproducing sufficiently successfully to 'win'
- capturing/converting resources more efficiently
in this first setup, all offspring are uniparental and no genes are mixed by any means other than mutation

Only one: an amoeba looks at a smaller amoeba with love and says, 'One day all this will be yours...'. In the next panel, the same amoeba looks at a second smaller amoeba, saying, '...unless it is yours. Depends who dies first.'

Theorem

Now consider a binary fission from $x_{t}$ , yielding one perfect clone and one mutant clone $x_{t}^{'}$ where mutation $(x_{t + 1} - x_{t}) \sim P_{m}$ .

Define the next 'step', $x_{t + 1}$ as whatever mutant offspring $x_{t}^{'}$ eventually happens to be successfully selected vs a perfect clone, according to the selection function on their fitness differential. (If the perfect clone gets selected, it may take many intermediate generations to constitute a 'step' here.) Denote by $α_{s}$ the resulting normalisation constant over mutations.

So the distribution over $x_{t + 1}$ given $x_{t}$ is

$P (x_{t + 1} | x_{t}) = α_{s} P_{m} (x_{t + 1} - x_{t}) P_{s} (f (x_{t + 1}) - f (x))$

Call the mutation $ϵ = x_{t + 1} - x_{t}$ . Then we find

$\begin{matrix} P (ϵ | x_{t}) & = α_{s} P_{m} (ϵ) P_{s} (f (x_{t} + ϵ) - f (x_{t})) ≃ α_{s} P_{m} (ϵ) P_{s} (ϵ \cdot \nabla f (x_{t})) \end{matrix}$

by considering the directional derivative of $f$ along $ϵ$ at $x_{t}$ and the limit as $ϵ \to 0$ ^[2]. (Prior to this infinitesimal limit, we have instead the empirical approximation to the directional derivative.)

Now characterising $ϵ$ by length $r_{ϵ} = | ϵ |$ and angle-from-gradient $θ_{ϵ} = ∠ (\nabla f (x_{t}), ϵ)$

$P (ϵ | x_{t}) ≃ α_{s} g (r_{ϵ}) P_{s} (r_{ϵ} | \nabla f (x_{t}) | cos θ_{ϵ})$

At this point it is clear that our step procedure depends, stochastically, on how closely the direction of the mutations match the fitness function's gradient.

By inspecting the expected value of the step direction, $θ_{ϵ}$ , we can make a more precise claim

$\begin{matrix} E [θ_{ϵ} | x_{t}] & = \int P (ϵ | x_{t}) θ d ϵ ≃ \int α_{s} g (r_{ϵ}) P_{s} (r_{ϵ} | \nabla f (x_{t}) | cos θ_{ϵ}) θ_{ϵ} d ϵ \end{matrix}$

and finally, by noticing the integral of an odd function^[3] in $θ$

$E [θ_{ϵ} | x_{t}] ≃ 0$

Thus the update between steps, $ϵ$ , is a stochastic realisation of a variable whose orientation is, in expectation, exactly the same as that of the gradient $\nabla f (x_{t})$ of the fitness function.

By similar inspection of $E [r_{ϵ} | x_{t}]$ we can see that it is a monotonic function of $| \nabla f (x_{t}) |$ , depending on the particulars of $P_{m}$ and $P_{s}$ , which together provide a gradient-dependent 'learning rate'.

So natural selection in this form really is nothing but an implementation of unbiased stochastic gradient descent!

Discussion of simplifying assumptions

To what extent are the simplifying assumptions realistic? What happens to the equivalence when we relax any of the assumptions?

Fixed 'fitness function'

In real natural selection, the interaction between a changing environment and a dynamic distribution of organisms collaborating and competing leads to a time- and location-dependent fitness function.

Variable fitness functions can lead to interesting situations like evolutionarily stable equilibria with mixtures of genotypes, or time- or space-cyclic fitness functions, or (locally) divergent fitness functions, among other phenomena.

Such a nonstationary fitness function is comparable to the use of techniques like self-play in RL, especially in conjunction with Population-Based Training, but is less comparable to vanilla SGD.

As such it may be appropriate to think of real natural selection as performing something locally equivalent to SGD but globally more like self-play PBT.

Continuous fixed-dimensional genome and radially-symmetric mutation probability density

Moving from a continuous to a discrete genome means that the notion of a gradient is no longer defined in the same way, but we can still talk about empirical approximate gradients and differences.

The mechanisms which introduce mutations in real natural selection are certainly symmetrical in certain ways, but probably not in any way which straightforwardly maps to radial symmetry in a fixed-dimensional vector space.

Without radial symmetry, much of the mathematics goes through similarly, but instead of an unbiased estimate of the gradient direction, it is biased by the mutation sampling. As such, we might think of real natural selection as performing a biased stochastic gradient descent.

A comparison may be made to regularisation techniques (depending on whether they are construed as part of the training procedure or part of the objective function), or to the many techniques exploiting bias-variance tradeoffs in sampling-based gradient-estimation for RL, though these tend to be deliberately chosen with variance-reduction in mind, while natural selection may not exhibit such preferences.

Limit case to infinitesimal mutation

In reality, mutations are not infinitesimal, but in practice very small relative to the genome. If we do not take the limit, instead of an exact directional derivative, we find an empirical-approximate directional derivative, yielding empirical-approximate stochastic gradient descent.

This means that in real natural selection, the implied 'step size' or 'learning rate' is coupled with the particulars of the selection strength, the variance of the stochastic gradient, and the degree of empirical approximation applied. In contrast, stochastic gradient descent per se need not couple these factors together.

A degenerate population of 1 or 2

If we expand the population to arbitrary size, it is possible to retrieve the equivalence with additional assumptions.

Instead of a parent individual and cloned and mutated offspring individuals, considering parent and offspring populations, the same reasoning and proof is immediately applicable if we assume that mutations arise sufficiently rarely to be either fixed or lost before the next mutation arises. In this case $P_{s}$ , the probability of selection, becomes the probability of fixation.

Of course this is not true for real natural selection.

If instead we allow for multiple contemporary mutant populations, an identical treatment can not be applied.

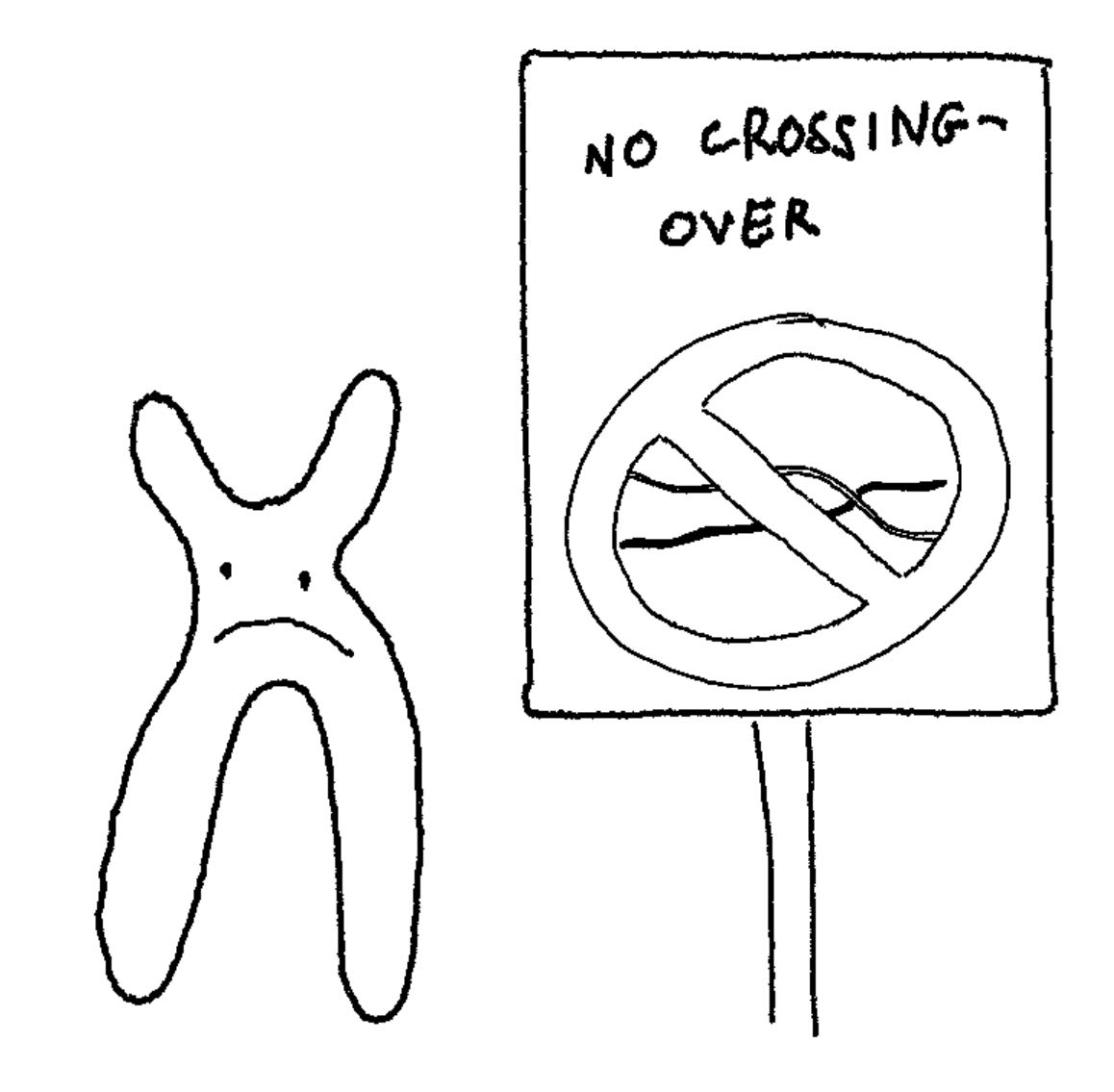
No recombination or horizontal transfer

No crossing-over: a sad chromosome stands beside a sign depicting a crossed-out recombination event, with text 'No crossing-over'

One of the most fascinating and mathematically complicating aspects of real natural selection is multiple heredity of genome elements, whether via horizontal transfer or sexual recombination.

The preceding proof of equivalence for natural selection and stochastic gradient descent rests on a model which does not include any notion of multiple heredity.

Recovering the equivalence allowing arbitrary population size and recombination

Interestingly, the 'complicating' factor of multiple heredity provides a way to retrieve the equivalence in the presence of multiple contemporary mutations, as long as we continue to consider the limit of infinitesimal mutations.

For a single-heredity population, with multiple contemporary mutant subpopulations, we must either model 'only one winner', or model an ongoing mixture of subpopulations of varying sizes, either of which $P_{s}$ is unable to model without modification.

On the other hand, in a multiple-heredity population, assuming eventually-universal mixing, and crucially continuing to assume a fixed fitness function (independent of the population mixture), a particular mutation must either fix or go extinct^[4].

Proof sketch

So let us consider (instead of $x_{t}$ and $x_{t + 1}$ ) $x_{t_{0}}$ and $x_{t_{1}}$ , representing the fixed part of the genotype at times $t_{0}$ and $t_{1} > t_{0}$ respectively, that is the initial genome $x_{0}$ plus all so-far-fixed mutations.

In the time between $t_{0}$ and $t_{1}$ the population will experience some integer number of mutation events (perhaps roughly Poisson-distributed but this is inessential for the proof), each of which is distributed according to $P_{m}$ . Furthermore, at time $t_{0}$ some mutations from earlier times may be 'in flight' and not yet fixed or extinct.

Assuming fixed fitness, and infinitesimal mutations, we can represent the probability of fixation by time $t_{1}$ , namely $P_{f}$ with exactly the same properties as formerly assumed for $P_{s}$ ^[5]. Thus each mutation fixed between $t_{0}$ and $t_{1}$ satisfies exactly the same unbiased-gradient-sampling property derived earlier, and so, therefore, does their sum $x_{t_{1}} - x_{t_{0}}$ .

This relies on all in-flight mutations not affecting the fitness differential, and thus $P_{f}$ , of their contemporaries, which is certainly the case in the limit of infinitesimal mutations, but not the case for real natural selection.

Summary of additional assumptions

Eventually-universal mixing

In particular, this means no speciation.

NB we also rely on 4. the limit to infinitesimal mutations, in an additional capacity. We also exclude all 'self-play-like' interactions arising from the larger population by relying further on 1. fixed 'fitness function'.

It may be feasible to retrieve a similar equivalence without excluding population-dependent fitness interactions with a different framing, for example considering gradients over 'mixed strategies' implied by population distributions.

Conclusion

Natural selection, under certain conditions, carries out an implementation of stochastic gradient descent. As such, analogies drawn from one to the other are not baseless; we should, however, examine the necessary assumptions and be mindful of the impact of departures from those assumptions.

In particular, two sets of assumptions are presented here which together are sufficient to retrieve an equivalence:

Fixed 'fitness function' or objective function mapping genome to continuous 'fitness score'
Continuous fixed-dimensional genome
Radially symmetric mutation probability density
Limit case to infinitesimal mutation
A degenerate population of 1 or 2
No recombination or horizontal transfer

or, keeping assumptions 1 to 4 and relaxing assumptions 5 and 6

Eventually-universal mixing

This is not enough to cover all instances of real natural selection, but provides an approximate mapping from many instances.

Assumptions 2 and 3 together yield 'unbiased' SGD, and in their absence varying degrees of bias arise.

Assumption 1 rules out, most importantly, 'self play' and 'population-based' aspects of natural selection, which have other analogies in machine learning but which are firmly absent from vanilla SGD.

Further work could uncover other parameters of the emergent SGD, such as the variance of the implied gradient, the size of the implicit learning rate, the bias caused by relaxing assumption 3, or quantify the coupling between those factors.

Further scrutiny, especially of the assumptions related to population, 1, 5, 6, and 7, could better quantify the effect of making weaker or different assumptions.

This can be justified in a few ways
- If fitness is something like an Elo rating then a Boltzmann distribution is implied
- If we want to extend the two-individual case to the n-individual case but remain invariant to the arbitrary choice of 'baseline' fitness score, then a normalised ratio of exponentials is implied
- We may further appeal to the maximum entropy property of Boltzmann distributions as a natural choice
↩︎
The directional derivative in question is, for $ϵ = | ϵ | u_{ϵ}$ ,

$\begin{matrix} lim | ϵ | \to 0 f (x_{t} + ϵ) - f (x_{t}) & = | ϵ | lim | ϵ | \to 0 \frac{f (x_{t} + | ϵ | u_{ϵ}) - f (x_{t})}{| ϵ |} = | ϵ | (u_{ϵ} \cdot \nabla f (x_{t})) = ϵ \cdot \nabla f (x_{t}) \end{matrix}$ ↩︎
Cautious readers may note that the integral as presented is not posed in the right coordinate system for its integrand.

By a coordinate transformation from Euclidean to hyperspherical coordinates, centred on $0$ , with $\nabla f (x_{t})$ providing the principal axis, $r$ the radial length, $θ$ the principal angular coordinate, and $ϕ$ the other $n - 2$ angular coordinates with axes chosen arbitrarily orthogonally,

$\begin{matrix} E [θ | x_{t}] & ≃ \int α_{s} g (r) P_{s} (r | \nabla f (x_{t}) | cos θ) θ d ϵ = \int α_{s} g (r) P_{s} (r | \nabla f (x_{t}) | cos θ) θ ∣ ∣ ∣ \frac{\partial (r, θ, ϕ)}{\partial (ϵ)} ∣ ∣ ∣ d r d θ d ϕ = \int_{0}^{\infty} \int_{- π}^{π} α_{s} g (r) P_{s} (r | \nabla f (x_{t}) | cos θ) θ [\int_{[0, π]^{n - 2}} ∣ ∣ ∣ \frac{\partial (r, θ, ϕ)}{\partial (ϵ)} ∣ ∣ ∣ d ϕ] d θ d r = \int_{0}^{\infty} \int_{- π}^{π} α_{s} g (r) P_{s} (r | \nabla f (x_{t}) | cos θ) θ [\int_{[0, π]^{n - 2}} r^{n - 1} h (ϕ) d ϕ] d θ d r = \int_{0}^{\infty} \int_{- π}^{π} α_{s} g (r) P_{s} (r | \nabla f (x_{t}) | cos θ) θ k r^{n - 1} d θ d r = \int_{0}^{\infty} α_{s} k g (r) r^{n - 1} [\int_{- π}^{π} P_{s} (r | \nabla f (x_{t}) | cos θ) θ d θ] d r = 0 \end{matrix}$

where we use the fact that the hyperspherical Jacobian $\frac{\partial (r, θ, ϕ)}{\partial (ϵ)}$ is independent of its principal angular coordinate $θ$ and denote by $k r^{n - 1}$ the result of integrating out the Jacobian over the other angular coordinates, and again noting that the symmetrical integral over an odd function is zero. ↩︎
If we do not have a fixed fitness function, and in particular, if it is allowed to vary dependent on the distribution of the population, there are many evolutionarily stable equilibria which can arise where some trait is stably never fixed nor extinguished, but rather persists indefinitely in some proportion of the population. (A classic example is sex ratios.) ↩︎
We can be more precise if we have $P_{f} : R^{+} \to R \to [0, 1]$ where the additional first parameter represents time-elapsed, so that $P_{f} (δ t, δ f)$ is the probability of a mutation with fitness delta $δ f$ being fixed after elapsed time $δ t$ .

Here we impose on $P_{f} (δ t)$ (for fixed $δ t$ time-elapsed) the same monotonicity requirement over fitness differential as imposed on $P_{s}$ before.

The various 'in-flight' and intervening mutations in the proof also therefore implicitly carry with them $t_{m}$ , the time they emerged, and the additional argument to $P_{f}$ is thus $δ t = t_{1} - t_{m}$ .

In practice we should expect $P_{f}$ to vary time-wise as a monotonically nondecreasing asymptote, but this property is not required for the proof. ↩︎

EvolutionGradient DescentMachine Learning (ML)MATS ProgramAI

Frontpage

70 Ω 27

Mentioned in

57Voting Results for the 2022 Review

27Deliberation Everywhere: Simple Examples

17Terminology: <something>-ware for ML?

New Comment

19 comments, sorted by

top scoring

Click to highlight new comments since: Today at 5:24 AM

[-]nostalgebraist1yΩ12270

This post introduces a model, and shows that it behaves sort of like a noisy version of gradient descent.

However, the term "stochastic gradient descent" does not just mean "gradient descent with noise." It refers more specifically to mini-batch gradient descent. (See e.g. Wikipedia.)

In mini-batch gradient descent, the "true" fitness^[1] function is the expectation of some function over a data distribution $ρ$ . But you never have access to this function or its gradient. Instead, you draw a finite sample from $ρ$ , compute the mean of $\nabla L$ over the sample, and take a step in this direction. The noise comes from the variance of the finite-sample mean as an estimator of the expectation.

The model here is quite different. There is no "data distribution," and the true fitness function is not an expectation value which we could noisily estimate with sampling. The noise here comes not from a noisy estimate of the gradient, but from a prescribed stochastic relationship ( $P_{s}$ ) between the true gradient and the next step.

I don't think the model in this post behaves like mini-batch gradient descent. Consider a case where we're doing SGD on a vector $x$ , and two of its components $x_{i}, x_{j}$ have the following properties:

The "true gradient" (the expected gradient over the data distribution) is 0 in the $x_{i}$ and $x_{j}$ directions.
The $x_{i}$ and $x_{j}$ components of the per-example gradient are perfectly (positively) correlated with one another.

If you like, you can think of the per-example gradient as sampling a single number $z$ from a distribution with mean 0, and setting the $x_{i}$ and $x_{j}$ components to $a_{i} z$ and $a_{j} z$ respectively, for some positive constants $a_{i}, a_{j}$ .

When we sample a mini-batch and average over it, these components are simply $a_{i} ¯ z$ and $a_{j} ¯ z$ , where $¯ z$ is the average of $z$ over the mini-batch. So the perfect correlation carries over to the mini-batch gradient, and thus to the SGD step. If SGD increases $x_{i}$ , it will always increase $x_{j}$ alongside it (etc.)

However, applying the model from this post to the same case:

Candidate steps are sampled according to $P_{m}$ , which is radially symmetric. So (e.g.) a candidate step with positive $x_{i}$ and negative $x_{j}$ is just as likely as one with both positive, all else being equal.
The probability of accepting a candidate step depends only on the true gradient^[2], which is 0 in the directions of interest. So, the $x_{i}$ and $x_{j}$ components of a candidate step have no effect on its probability of selection.

Thus, the the $x_{i}$ and $x_{j}$ components of the step will be uncorrelated, rather than perfectly correlated as in SGD.

Some other comments:

The descendant-generation process in this post seems very different from the familiar biological cases it's trying to draw an analogy to.
- In biology, "selection" generally involves having more or fewer descendants relative to the population average.
- Here, there is always exactly one descendant. "Selection" occurs because we generate (real) descendants by first generating a ghostly "candidate descendant," comparing it to its parent (or a clone of its parent), possibly rejecting it against the parent and drawing another candidate, etc.
- This could be physically implemented in principle, I guess. (Maybe it has been, somewhere?) But I'm not convinced it's equivalent to any familiar case of biological selection. Nor it is clear to me how close the relationship is, if it's not equivalence.
The connection drawn here to gradient descent is not exact, even setting aside the stochastic part.
- You note that we get a "gradient-dependent learning rate," essentially because $P_{s}$ can have all sorts of shapes -- we only know that it's monotonic, which gives us a monotonic relation between step size and gradient norm, but nothing more.
- But notably, (S)GD does not have a gradient-dependent learning rate. To call this an equivalence, I'd want to know the conditions under which the learning rate is constant (if this is possible).
- It is also is possible this model always corresponds to vanilla GD (i.e. with a constant learning rate), except instead of ascending $f$ , we are ascending some function related to both $P_{s}$ and $f$ .
This post calls $f$ the "fitness function," which is not (AFAIK) how the term "fitness" is used evolutionary biology.
- Fitness in biology typically means "expected number of descendants" (absolute fitness) or "expected change in population fraction" (relative fitness).
- Neither of these have direct analogues here, but they are more conceptually analogous to $P (x_{t + 1} | x_{t})$ than $f$ . The fitness should directly tell you how much more or less of something you should expect in the next generation.
- That is, biology-fitness is about what actually happens when we "run the whole model" forward by a timestep, rather than being an isolated component of the model.
- (In cases like the replicator equation, there is model component called a "fitness function," but the name is justified by its relationship to biology-fitness given the full model dynamics.)
- Arguably this is just semantics? But if we stop calling $f$ by a suggestive name, it's no longer clear what importance we should attach to it, if any. We might care about the quantity whose gradient we're ascending, or about the biology-fitness, but $f$ is not either of those.

^{^}
I'm using this term here for consistency with the post, though I call it into question later on. "Loss function" or "cost function" would be more standard in SGD.
^{^}
There is no such thing as a per-example gradient in the model. I'm assuming the "true gradient" from SGD corresponds to $\nabla f$ in the model, since the intended analogy seems to be "the model steps look like ascending $f$ plus noise, just like SGD steps look like descending the true loss function plus noise."

[-]Oliver Sourbut1y20

On to some specific responses.

[Of the first evolution model:] the true fitness function is not an expectation value which we could noisily estimate with sampling

a prescribed stochastic relationship ( $P_{s}$ ) between the true gradient and the next step.

Go back to my 'distribution of environment scenarios' lower-level model. Certainly this could induce correlations if we wanted it to, for basically the same reasons as in your example.

Here, there is always exactly one descendant.

On learning rates, I appreciate this remark. I called this out in the original as something for further research, but (for SCT reasons) I don't consider it especially important/urgent.

(S)GD does not have a gradient-dependent learning rate. To call this an equivalence, I'd want to know the conditions under which the learning rate is constant (if this is possible).

This post calls $f$ the "fitness function," which is not (AFAIK) how the term "fitness" is used evolutionary biology.

We might care about the quantity whose gradient we're ascending, or about the biology-fitness, but $f$ is not either of those.

$f$ is the quantity whose gradient we're ascending. And it's biology-fitness in the pre-operationalisation-as-fecundity/offspring sense.

Please let me know if I've missed anything that seems important to you - these are longish comments.

e.g. imagine characterising the sample-based loss estimate via mean and variance. For now, assume normal and homoscedastic (more spherical cows!). Is my claim about a monotonic selection prob arising from this then basically clear? There's some prob of 'accidentally' getting samples which invert the fitness order, but this prob decreases as the true fitness difference increases. (For non-normal or heteroscedastic, this still holds locally, but the coefficients will be different in different regions.) ↩︎

[-]nostalgebraist1y140

I no longer feel like I know what claim you're advancing.

In this post and in recent comments (1, 2), you've said that you have proven an "equivalence" between selection and SGD under certain conditions. You've used phrases like "mathematically equivalent" and "a proof of equivalence."

When someone tells me they have a mathematical proof that two things are equivalent, I read the word "equivalent" to mean "really, totally, exactly the same (under the right conditions)." I think this is a pretty standard way to interpret this kind of language. And in my critique, I argued -- I think successfully -- against this kind of equivalence.

From your latest comments, it appears that you are not claiming anything this strong. But now I don't know what you are claiming. For instance, you write here:

On the distribution of noise, I'll happily acknowledge that I didn't show equivalence. I half expect that one could be eked out at a stretch, but I also think this is another minor and unimportant detail.

Details that are "unimportant" in one context, or for making a particular argument, may be very important in some other context or argument^[1]. To take one example:

As I said elsewhere, any number of practical departures from pure SGD mess with the step size anyway (and with the gradient!) so this feels like asking for too much. Do we really think SGD vs momentum vs Adam vs ... is relevant to the conclusions we want to draw? (Serious question; my best guess is 'no', but I hold that medium-lightly.)

This all depends on "the conclusions we want to draw." I don't know which conclusions you want to draw, and surely the difference between these optimizers is not always irrelevant.

If I am, say, training a neural net, then I am definitely not going to be indifferent between Adam and SGD -- Adam is way faster! And even if you don't care about speed, just about asymptotic performance, the two find solutions with different characteristics, cf. the literature on the "adaptive optimization gap."

The profusion of different SGD-like optimizers is not evidence that the differences between them don't matter. It's the opposite: the differences matter a lot, and that's why people keep coming up with new variants. If all such optimizers were about the same, there'd be no reason to make new ones.

Or, consider that the analogy only holds for infinitesimal step size, on both sides^[2]. Yet the practical efficacy of SGD has much to do with the fact that it works fine even at large step sizes, up to some breaking point.

Until we tie down what we're trying to do, I don't know how to assess whether any of these distinctions are (ir)relevant or (un)important.

On another note, the fact that the gradient "comes out of the maths" does not seem very noteworthy to me. It's inevitable from the problem setup: everything is rotationally symmetric except , and we're restricted to function evaluations inside an $ϵ$ -ball, so we can't feel the higher-order derivatives of $f$ . As long as we're not analytically computing any of those higher derivatives, we should expect any direction appearing in the result to be a function of the gradient -- it's the only source of directionality available, the only thing that breaks the symmetry^[3].

Here the function of the gradient is just the identity, but I expect you'd still deem it "acceptable" if it were not, since it would still fall into the "class" of optimizers that includes Adam etc. (For Adam, the function involves the gradient and the buffers computed from it, which in turn require the introduction of a privileged basis.)

By these standards, what optimizer isn't equivalent to gradient descent? Optimizers that analytically compute higher-order derivatives, that's all I can come up with. Which is a strange place to draw a line in the sand, IMO: "all 0th and 1st order optimizers are the same, but 2nd+ order optimizers are different." Surely there are lots of important differences between different 0th and 1st order optimizers?

^{^}
The nice thing about a true equivalence result is that it's not context-dependent like this. All the details match, all at once, so we can readily apply the result in whatever context we like without having to check whether this context cares about some particular nuance that didn't transfer.
^{^}
We need this limit because the SGD step never depends on higher-order derivatives, no matter the step size. But a guess-and-check optimizer like selection can feel higher-order derivatives at finite step sizes.
^{^}
Likewise, we should expect a scalar like the step size to be some function of the gradient magnitude, since there aren't any other scalars in the problem (again, ignoring higher-order derivatives). I guess there's $f$ itself, but it seems natural to "quotient out" that degree of freedom by requiring the optimizer to behave the same way for $f$ and $f + c$ .

[-]Oliver Sourbut1y50Review for 2022 Review

Origin and summary

This post arose from a feeling in a few conversations that I wasn't being crisp enough or epistemically virtuous enough when discussing the relationship between gradient-based ML methods and natural selection/mutate-and-select methods. Some people would respond like, 'yep, seems good', while others were far less willing to entertain analogies there. Clearly there was some logical uncertainty and room for learning, so I decided to 'math it out' and ended up clarifying a few details about the relationship, while leaving a lot unresolved. Evidently for some readers this is still not crisp or epistemically virtuous enough!

I still endorse this post as the neatest explanation I'm aware of relating gradient descent to natural selection under certain approximations. I take the proof of the limiting approximation to be basically uncontroversial^[1], but I think my discussion of simplifying assumptions (and how to move past them) is actually the most valuable part of the post.

Overall I introduced three models of natural selection

an annealing-style degenerate natural selection, which is most obviously equivalent in the limit to a gradient step
a one-mutant-population-at-a-time model (with fixation or extinction before another mutation arises)
(in the discussion) a multi-mutations-in-flight model with horizontal transfer (which is most similar to real natural selection)

All three are (in the limit of small mutations) performing gradient steps. The third one took a bit more creativity to invent, and is probably where I derived the most insight from this work.

All three are still far from 'actual real biological natural selection'!

What important features of natural selection are missing?

Speciation!
- This is a very distinguishing and interesting feature of real biological natural selection
- All my models (one way or another) rule out speciation, which is called out but could be clearer in the post
- A model with gradients over 'mixed strategies' might be able to incorporate speciation
Variability of the fitness landscape
- The interaction of fitness dependent on population distribution is totally not covered by my models
- I called out Population-Based Training as the most obvious ML analogue to this
  - I think this is still basically right, though perhaps more broadly construed than the specific mechanism described in the PBT paper
Any within-lifetime things!
- Within-lifetime learning
- Sexual selection and offspring preference
- Cultural accumulation
- Epigenetics
Recombination hacks
- Anything with intragenomic conflict
- Transposons, segregation distortion, etc.

So what?

Another point I didn't touch on in this post itself is what to make of any of this.

Understanding ML

For predicting the nature of ML artefacts, I don't think speciation is relevant, so that's a point in favour of these models. I do think population-dependent dynamics (effectively self-play) are potentially very relevant, depending on the setting, which is why in the post I said,

As such it may be appropriate to think of real natural selection as performing something locally equivalent to SGD but globally more like self-play PBT.

One main conclusion people want to point to when making this kind of analogy is that selecting for thing-X-achievers doesn't necessarily produce thing-X-wanters. i.e. goal-misgeneralisation aka mesa-optimisation aka optimisation-daemons. I guess tightening up the maths sort of shores up this kind of conclusion?^[2]

Thomas Kwa has a nice brief list of other retrodictions of the analogy between gradient-based ML and natural selection.

How much can we pre-dict? When attempting to draw more specific conclusions (e.g. about particular inductive biases or generalisation), I think in practice analogies to natural selection are going to be screened off by specific evidence quite easily. But it's not clear that we can easily get that more specific evidence in advance, and for more generally-applicable but less-specific claims, I think natural selection gives us one good prior to reason from.

If we're trying to draw conclusions about intelligent systems, we should make sure to note that a lot of impressive intelligence-bearing artefacts in nature (brains etc.) are grown and developed within-lifetime! This makes the object of natural selection (genomes, mostly) something like hyperparameters or reward models or learning schedules or curricula rather than like fully-fledged cognitive algorithms.

In a recent exchange, 1a3orn shared some interesting resources which make similar connections between brain-like learning systems and gradient-based systems. More commonalities!

Understanding natural selection

Sometimes people want to understand the extent to which natural selection 'is optimising for' something (and what the exact moving pieces are). Playing with the maths here and specifying some semantics via the models has helped sharpen my own thinking on this. For example, see my discussion of 'fitness' here

The original pretheoretic term 'fitness' meant 'being fitted/suitable/capable (relative to a context)', and this is what Darwin and co were originally pointing to. (Remember they didn't have genes or Mendel until decades later!)

The modern technical usage of 'fitness' very often operationalises this, for organisms, to be something like number of offspring, and for alleles/traits to be something like change in prevalence (perhaps averaged and/or normalised relative to some reference).

So natural selection is the ex post tautology 'that which propagates in fact propagates'.

If we allow for ex ante uncertainty, we can talk about probabilities of selection/fixation and expected time to equilibrium and such. Here, 'fitness' is some latent property, understood as a distribution over outcomes.

If we look at longer timescales, 'fitness' is heavily bimodal: in many cases a particular allele/trait either fixes or goes extinct^[3]. If we squint, we can think of this unknown future outcome as the hidden ground truth of latent fitness, about which some bits are revealed over time and over generations.

A 'single step' of natural selection tries out some variations and promotes the ones which in fact work (based on a realisation of the 'ex ante' uncertain fitness). This indeed follows the latent fitness gradient in expectation.

In this ex ante framing it becomes much more reasonable to treat natural selection as an optimisation/control process similar to gradient descent. It's shooting for maximising the hidden ground truth of latent fitness over many iterations, but it's doing so based on a similar foresight-free local heuristic like gradient descent, applied many times.

How can we reconcile this claim with the fact that the operationalised 'relative fitness' often walks approximately randomly, at least not often sustainedly upward^[4]? Well, it's precisely because it's relative - relative to a changing series of fitness landscapes over time. Those landscapes change in part as a consequence of abiotic processes, partly as a consequence of other species' changes, and often as a consequence of the very trait changes which natural selection is itself imposing within a population/species!

So, I think, we can say with a straight face that natural selection is optimising (weakly) for increased fitness, even while a changing fitness landscape means that almost by definition relative fitness hovers around a constant for most extant lineages. I don't think it's optimising on species, but on lineages (which sometimes correspond).^[5]

In further (unpublished) mathsy scribbles around the time of this post, I also played with rederiving variations on the Price equation, and spent some time thinking about probabilities of fixation and time-to-fixation (corroborating some of Eliezer's old claims). These were good exercises, but not obviously worth the time to write up.

I was also working with Holly Elmore on potential insights from some more specific mechanisms in natural selection regarding intragenomic conflict. I learned a lot (in particular about how 'computer sciencey' a lot of biological machinery is!) but didn't make any generalisable insights. I do expect there might be something in this area though.

Understanding control

The connections here were part of a broader goal of mine to understand 'deliberation' and 'control'. I've had a hard time making real progress on this since (in part due to time spent on other things), but I do feel my understanding of these has sharpened usefully. Spending some time closely pondering the connection between different optimisation procedures definitely provided some insights there.

I recently came across the 'complex systems' kind of view on adaptation and control and wonder if I might be converging in that direction.

The biggest puzzle-piece I want to see cracked regards the temporal extent of predictors/deliberators. Greater competence seems tightly linked to the ability to do 'more lookahead'. I think this is one of the keys which gives rise to 'deliberate exploration'/'experimentation', which is one of my top candidate intelligence explosion feedback loops^[6]. My incomplete discussion of deliberation was heading in that direction. Some more recent gestures include some disorganised shortform discussion and my planner simulator conjecture:

something like, 'every (simplest) simulator of a planner contains (something homomorphic to) a planner'.

How far are we stretching to call this 'equivalence'?

The proofs demonstrate that all three models of natural selection perform a noisy realisation of a gradient step (in the limit of small mutations).

As I called out in the post, I didn't pay much attention to step size, nor to the particular stochastic distribution of updates. To my mind, this is enough to put the three models of natural selection equivalent to something well within the class of 'stochastic gradient methods'^[7]. 'SGD' is often used to refer to this broader class of methods, but it might be a bit misleading to use the term 'SGD' without qualification, which after all is often used to refer to a more specific stochastic gradient implementation.

nostalgebraist calls me out on this

the noise in your model isn't distributed like SGD noise, and unlike SGD the the step size depends on the gradient norm.

which is the most attentive criticism I've had of this post.

Aren't we stretching things quite far if we're including momentum methods and related, with history/memory-sensitive updates? Note that natural selection can implement a kind of momentum too (e.g. via within-lifetime behavioural stuff like migration, offspring preference, and sexual selection)! Neither my models nor the 'SGD' they're equivalent to exhibit this.

nostalgebraist's dissatisfaction notwithstanding; these are good criticisms but appear miss a lot of the caveats already present in the original post. ↩︎
I never thought this conclusion needed shoring up in the first place, and in the cases where it's not accepted, it's not clear to me whether mathing it out like this is really going to help. ↩︎
In cases where the relative fitness of a trait corresponds with its prevalence, there can be a dynamic equilibrium at neither of these modes. Consider evolutionary stable strategies. But the vast majority of mutations ever have hit the 'extinct' attractor, and a lot of extant material is of the form 'ancestor of a large proportion of living organisms'. ↩︎
Though note we do see (briefly?) sustained upward fitness in times of abundance, as notably in human population and in adaptive radiation in response to new resources, habitats, and niches becoming available. ↩︎
Now, if the earlier instances of now-extinct lineages were somehow evolutionarily 'frozen' and periodically revived back into existence, we really would see that natural selection pushes for increased fitness. But because those lineages aren't (by definition) around any more, the fitness landscape's changes over time are under no obligation to be transitive, so in fact a faceoff between a chicken and a velociraptor might tell a different story. ↩︎
I think exploration heuristics are found throughout nature, some 'intrinsic curiosity' reward shaping gets further (e.g. human and animal play), but 'deliberate exploration' (planning to arrange complicated scenarios with high anticipated information value) really sets humans (and perhaps a few other animals) apart. Then with cultural accumulation and especially the scientific revolution, we've collectively got really good at this deliberate exploration, and exploded even faster. ↩︎
e.g. vanilla SGD, momentum, RMSProp, Adagrad, Adam, ... ↩︎

[-]gwern1y40

Aren't we stretching things quite far if we're including momentum methods and related, with history/memory-sensitive updates? Note that natural selection can implement a kind of momentum too (e.g. via within-lifetime behavioural stuff like migration, offspring preference, and sexual selection)! Neither my models nor the 'SGD' they're equivalent to exhibit this.

Maybe you're just not committed enough to momentum.

[-]Oliver Sourbut1y10

Haha mind blown. Thanks for the reference! Different kind of momentum, but still...

[-]gwern1y20

Is it all that different? SGD momentum methods are usually analogized literally to 'heavy balls' etc. And I suspect, given how some gradient-update-based meta-learning methods work, you can cast within-lifetime updates as somehow involving a momentum.

[-][anonymous]3y40

This looks so great Ollie! I

[-][anonymous]3y40

Makes me want to do the same thing for markets

[-]Oliver Sourbut3y40

Thanks Nathan! Hmm, that sounds interesting. I guess with a market, the population and non fixed nature of the 'fitness' landscape are quite important, like in real natural selection. So you might need to make a similar move and assume it's 'locally' stationary? I wonder how that corresponds to PBT and self-play. I wish I knew more about markets :)

[-]Youlian3y30

I haven't read through the parent post yet, but I'm excited to do so tonight for almost precisely this reason.

It feels like markets, neural networks, evolution, human organizational hierarchies, and any number of other systems resolve into some common structure, with individual agents performing some computation, passing around some summary messages, and then thriving or diminishing based on the system's performance on some task.

I'd be interested in an underlying mathematical model that unifies many of these fields. A mapping between natural selection and gradient descent is a useful piece of that puzzle.

[-]gwern3y40

The Price equation :)

[-]Youlian3y10

Thanks for the pointer! Looks like I've got my reading assignments lined up :-).

[-]DirectedEvolution3y30

I haven’t worked through the proof yet, but wanted to point out that this is especially relevant to aptamer generation via SELEX. There, the simplifying assumptions are very close to reality. This is my own research topic, and it’s under-theorized, so it’s great to see some relevant work in the space.

[-]Oliver Sourbut3y30

Oh, great! You're welcome. I searched for 'aptamer SELEX' and it looks very interesting :)

[-]Martín Soto2y10

Wow, this post is great!

[-]Oliver Sourbut3y10

I'm informed^[1] that the concept I employed in the 'recovering the equivalence' section of the 'fixed parts' and 'in flight mutations' is similar to the 'coalescence' of 'Coalescent theory' which is an apparently relatively niche Biology tool, whose applications appear interesting (if unrelated) from a cursory look.

by Holly Elmore, thanks! ↩︎

[-]Oliver Sourbut3y10

Other resources

I'd love to gather more inputs on different conditions for equivalences (and non-equivalences!) like this.

While writing up this proof, I came across Whitelam et al - Correspondence between neuroevolution and gradient descent, a paper in Nature Communications (https://www.nature.com/articles/s41467-021-26568-2) which, upon skimming, appears to reach a similar, though less general conclusion. I have some trouble understanding their notation though.

[-]Steveot3y20

It's not a mathematical argument, but here I first came across such an analogy drawn between training of neural networks and evolution, and a potential interpretation of what it means in terms of sample-(in)efficiency.

Moderation Log