Over the last couple of years, mechanistic interpretability has seen substantial progress. Part of this progress has been enabled by the identification of superposition as a key barrier to understanding neural networks (Elhage et al., 2022) and the identification of sparse autoencoders as a solution to superposition (Sharkey et al., 2022; Cunningham et al., 2023; Bricken et al., 2023). 

From our current vantage point, I think there’s a relatively clear roadmap toward a world where mechanistic interpretability is useful for safety. This post outlines my views on what progress in mechanistic interpretability looks like and what I think is achievable by the field in the next 2+ years. It represents a rough outline of what I plan to work on in the near future.

My thinking and work is, of course, very heavily inspired by the work of Chris Olah, other Anthropic researchers, and other early mechanistic interpretability researchers. In addition to sharing some personal takes, this article brings together - in one place - various goals and ideas that are already floating around the community. It proposes a concrete potential path for how we might get from where we are today in mechanistic interpretability to a world where we can meaningfully use it to improve AI safety. 

Key frameworks for understanding the agenda

Framework 1: The three steps of mechanistic interpretability

I think of mechanistic interpretability in terms of three steps:

The three steps of mechanistic interpretability^[1]:

1. Mathematical description: In the first step, we break the neural network into constituent parts, where the parts are simply unlabelled mathematical objects. These may be e.g. neurons, polytopes, circuits, feature directions (identified using SVD/NMF/SAEs), individual parameters, singular vectors of the weight matrices,  or other subcomponents of a network. 
2. Semantic description: Next, we generate semantic interpretations of the mathematical object (e.g. through feature labeling). In other words, we try to build a conceptual model of what each component of the network does. 
3. Validation: We need to validate our explanations to ensure they make good predictions about network behavior. For instance, we should be able to predict that ablating a feature with a purported ‘meaning’ (such as the 'noun gender feature') will have certain predictable effects that make sense given its purported meaning (such as the network becoming unable to assign the appropriate definitive article to nouns). If our explanations can’t be validated, then we need to identify new mathematical objects and/or find better semantic descriptions.

The field of mechanistic interpretability has repeated this three-step cycle a few times, cycling through explanations given in terms of neurons, then other objects such as SVD/NMF directions or polytopes, and most recently SAE directions. 

My research over the last couple of years has focused primarily on identifying the right mathematical objects for mechanistic explanations. I expect there’s still plenty of work to do on this step in the next two years or so (more on this later). To guide intuitions about how I plan to pursue this, it’s important to understand what makes some mathematical objects better than others. For this, we have to look at the description accuracy vs. description length tradeoff.

Framework 2: The description accuracy vs. description length tradeoff

You would feel pretty dissatisfied if you asked someone for a mechanistic explanation of a neural network and they proceeded to read out of the float values of the weights. But why is this dissatisfying? Two reasons:

1. When describing the mechanisms of any system, be it an engine, a solar system, or a neural network, there is always a tradeoff between description accuracy and description length. The network is the most accurate mathematical description of itself, but it has a very long mathematical description length. 
2. It isn’t even a semantic description at all. This makes things difficult to understand because we can’t easily intuit mathematical descriptions. To understand what the weights in the network ‘mean’, we need semantic descriptions^[2]. 

Part of our job in mechanistic interpretability (and the framework used in this agenda) is to push the Pareto frontier of current mechanistic interpretability methods toward methods that give us the best tradeoff between description accuracy and description length. We’re therefore not only optimizing for accurate descriptions; we’re also optimizing for shorter descriptions. In other words, we want to find objects that admit mathematical descriptions that use as few objects as possible but that capture as much of what the network is doing as possible. Furthermore, we want short semantic descriptions for these objects, such that we need few words or concepts to describe what they do. 

To summarize, we’re in fact optimizing our interpretability methods according to four constraints here: 

1. Mathematical description accuracy - How good the approximation of the original network’s behaviour is; 
2. Mathematical description length - How many mathematical objects the network is decomposed into; 
3. Semantic description accuracy - How good the predictions made by the conceptual model of the network are; 
4. Semantic description length - How many words/concepts are needed to define the conceptual model of the network. 

Inadequacy according to at least one of these constraints has been the downfall of several previous interpretability approaches:

• Non-mechanistic approaches, such as attribution maps (e.g. Simonyan et al., 2013) have been demonstrated often to yield misleading (low accuracy) semantic descriptions (Adebayo et al., 2018; Kindermans et al., 2017). 
• Using neurons as the mathematical objects to interpret (e.g. Olah et al., 2020) yields too-long mathematical descriptions and even more too-long semantic descriptions due to polysemanticity.
• Using SVD/NMF/ICA directions (e.g. Schubert et al., 2021; Voss et al., 2021) instead of neurons arguably improves the mathematical description length, but the semantic description length is still too long due to polysemanticity.
• Using polytopes (Balestriero and Baraniuk, 2018; Black et al., 2022) as the fundamental mathematical object yields much too long mathematical descriptions^[3], even if they are in some sense ‘more accurate’ with regard to the network’s nonlinear structure than directions.

This leads us to one of the core methods in this agenda that so far appears to perform well according to our four constraints: sparse autoencoders (SAEs). 

The unreasonable effectiveness of SAEs for mechanistic interpretability

SAEs have risen in popularity over the last year as a candidate solution to the problem of superposition in mechanistic interpretability (Elhage et al., 2022; Sharkey et al., 2022; Cunningham et al., 2023; Bricken et al., 2023)

SAEs are very simple. They consist of an encoder (which is just a linear transformation followed by a nonlinear activation function) and a decoder (or ‘dictionary’) whose features are constrained to have fixed length. The loss function used to train them has two components: (1) The reconstruction loss, so that their output approximates their input; (2) The sparsity loss, which penalizes the encoder outputs to be sparse.

I harp on about SAEs so much that it’s become a point of personal embarrassment. But the reason is because SAEs capture so much of what we want in a mechanistic interpretability method:

1. The reconstruction loss trains the SAE features to approximate what the network does, thus optimizing for mathematical description accuracy.
2. The sparsity penalty trains the SAE to activate fewer features for any given datapoint, thus optimizing for shorter mathematical description length. 
3. The features identified by SAEs appear more monosemantic than other methods identified so far (Cunningham et al., 2023; Bricken et al., 2023). And unlike clustering, they factorize the network’s activations into compositional components, which means they yield modular descriptions. For both these reasons, they therefore perform well according to semantic description length. 

It would be nice to have a formal justification for why we should expect sparsification to yield short semantic descriptions. Currently, the justification is simply that it appears to work and a vague assumption about the data distribution containing sparse features. I would support work that critically examines this assumption (though I don't currently intend to work on it directly), since it may yield a better criterion to optimize than simply ‘sparsity’ or may yield even better interpretability methods than SAEs.

The last selling point of SAEs that I'll mention is that the SAE architecture and training method are very flexible: They lend themselves to variants that can be used for much more than merely identifying features in activations. For instance, they could be used to identify interactions between features in adjacent layers (sparse transcoders) or could potentially be used to identify whole circuits (meta-SAEs). We’ll have more to say about transcoders and meta-SAEs later.

Framework 3: Big data-driven science vs. Hypothesis-driven science

The last framework driving this agenda is a piece of ‘science ideology’. 

In the last few decades, some branches of science have radically changed. They’ve moved away from purely hypothesis-driven science toward a ‘big data’-driven paradigm. 

In hypothesis-driven science, you make an hypothesis about some phenomenon, then collect data that tests the hypothesis (e.g. through experiments or surveys). Think ‘testing general relativity’; ‘testing whether ocean temperature affects atmospheric sulfur levels’; or ‘testing whether smoking causes lung cancer’, etc.

Big Data-driven science does things differently. If Big Data-driven science had a motto, it’d be “Collect data first, ask questions later”. Big Data-driven science collects large datasets, then computationally models the structure in this data. The structure of those computational models suggests hypotheses that can be tested in the traditional way. The Big Data-driven approach has thrived in domains of science where the objects of study are too big, complex, or messy for humans to have much of a chance of comprehending it intuitively, such as genetics, computational neuroscience, or proteomics. 

In mechanistic interpretability, I view work such as “Interpretability in the Wild: A Circuit for Indirect Object Identification in GPT-2 small” (Wang et al., 2023) as emblematic of ‘hypothesis-driven science’. They identified a task (‘indirect object identification’ - IOI) and asked if they could identify circuits of nodes (attention heads at particular token positions) that performed this task on a dataset they constructed. This was a very solid contribution to the field. However, to my personal research taste it felt like the wrong way to approach mechanistic interpretability in a few ways: 

• Is IOI a ‘task’ from the network’s perspective? Does it chop up tasks in the same way?
• Are the objects studied here (attention heads at particular token indices) fundamental objects from the network’s perspective? Are any objects missing?
• If we studied a different artificial dataset for a different task, would we come to different conclusions about which heads do what?

To me, it felt like coming at mechanistic interpretability from a human perspective when, instead, we should be coming at it from the network’s perspective: 

• We should identify tasks the way a network breaks up taskspace instead of choosing individual tasks ourselves; 
• Rather than choosing parts of the distribution that we think might explain the most about an hypothesis we’re currently evaluating, we should look at behavior of network components over the whole distribution and ‘let the network decide’ which are the relevant sub-distributions; 
• We should make hypotheses in terms of objects that the network considers fundamental, rather than deciding for ourselves what the fundamental objects are. 

I contend that mechanistic interpretability is a domain that needs a Big Data-driven approach more than usual. Neural networks are too big, too messy, too unintuitive to comprehend unless we map out their components in a principled way. Without mapping the space first, we are flying blind and are bound to get lost. To be absolutely clear, Big Data-driven science does not replace hypothesis-driven science; it just augments hypothesis formation and testing. But I think that without this augmentation, mechanistic interpretability is doomed to flounder (see also Wentworth on this theme).

Fortunately, neural networks are very well suited to Big Data-driven science, because it is so easy to collect data from them. It's even easy to directly collect data about their causal structure (i.e. information about their gradients and architecture), unlike in most areas of science!   

The power of Big Data-driven science is a background assumption for much of my research. For me, it motivated the search for SAEs as a scalable, unsupervised structure-finding method, which can be applied to whole networks and datasets, and which might help reveal the objects that the network considers fundamental. It privileges big datasets that contain all the things that a network does such that, when we analyze these big datasets, the interpretable structure of the network naturally falls out thanks to unsupervised methods. And this bit of science ideology also motivates most of the objectives in the agenda. 

Sparsify: The Agenda

I envision a mechanistic interpretability tech tree something like this:

I’ll explain what each of the objectives here mean in more detail below. The main convergent objective of the agenda is satisfactory whole-network mechanistic interpretability, which I think could open up a range of safety-relevant applications. Most of the other objectives can be framed as trying to improve our mathematical and semantic descriptions by improving their accuracy vs. length Pareto frontiers. 

The objectives for my research over the next 2+ years are the following (with high-variance estimates for timelines that feel somewhat achievable for a community of researchers): 

1. Objective 1: Improved SAEs: Get good at taking features out of superposition using SAEs by pushing the Pareto frontier of our mathematical descriptions closer to optimal and reducing computational costs. (Starting in 0 Months - until 1y)
2. Objective 2: Decompiled networks: Networks that do computation in the feature basis. (Starting in 2 months - until 1.5y)
3. Objective 3: Abstraction above raw decompilations: Identify circuits and, if necessary for short enough descriptions, make principled abstractions above the mechanistic layer of abstraction. (Starting in 3 months - until 2y)
4. Objective 4: Deep Description: Going beyond automated feature labeling by integrating different kinds of description together. (Starting in 6 months - until future)
5. Objective 5: Applications of mechanistic interpretability: Including mechanistic interpretability-based evals; alignment method profiling; capability prediction; and, potentially, robust to training mechanistic interpretability. (Starting 6 months - until future)

Objective 1: Improving SAEs

I think there’s lots of room for improvement on current SAEs. In particular,

• Benchmarking SAEs
• Fixing SAE pathologies
• Applying SAEs to attention
• Better hyperparameter selection methods
• Computationally efficient sparse coding

Benchmarking SAEs

At present, it’s difficult to know when SAEs should be considered ‘good’. We need to devise principled metrics and standardized ways to compare them. This will be important both for identifying good SAEs trained on models and for developing improvements on SAEs and SAE training methods.

Fixing SAE pathologies

Current SAEs exhibit a few pathologies that make them suboptimal as mathematical descriptions in terms of both description accuracy and description length. My collaborators and I (through MATS and Apollo Research) are working on a few posts that aim to address them. Here we share an overview of a few early results:

• Finding functionally relevant features using e2e SAEs (Upcoming post -  Dan Braun, Jordan Taylor, Lee Sharkey): There is no guarantee that the directions that SAEs find are ‘functionally relevant’ to the network; SAEs currently just find directions that reconstruct a layer’s activations well while being sparse. We demonstrate that the standard reconstruction loss used to train SAEs is not optimal for learning functionally relevant features and show that an end-to-end (e2e) loss function, which reconstructs activations and distributions in later layers, improves the functional relevance of the features learned. End-to-end training means a smaller, more accurate set of SAE features can explain the same amount of network function, implying the typical way of training SAEs is suboptimal according to mathematical description accuracy and length. 
• Choosing better sparsity penalties than L1 (Upcoming post -  Ben Wright & Lee Sharkey): There is reason to believe that $L_1$ is a suboptimal sparsity penalty: In toy datasets, where we know the ground truth features, an $L_1$ penalty leads to too many features being learned compared with ground truth features. This leads to suboptimal mathematical description length. We propose a simple fix: Use $L_{0<p<1}$ instead of $L_1$, which seems to be a Pareto improvement over $L_1$ (at least in some real models, though results might be mixed) in terms of the number of features required to achieve a given reconstruction error.
• Addressing feature suppression (link)(Ben Wright & Lee Sharkey): When SAE encoders guess how much of a feature is present in their input, they systematically undershoot. This is due to their optimizing both reconstruction and $L_1$, resulting in suboptimal mathematical description accuracy. Ben looked at a way to fix this undershooting. We think success, while real, was modest. We think there are probably ways to improve upon the results of this work.

Applying SAEs to attention

Some work (unrelated to my collaborators and I) demonstrate that SAEs work reasonably well when applied to attention block outputs (Kissane et al., 2024). However, so far, the inner workings of attention blocks remain somewhat enigmatic and attention head superposition (Jermyn et al., 2023) remains unresolved. 

How best to apply SAE-like methods to decompose attention blocks? We have investigated two approaches in parallel:

• Gated Attention Blocks: Preliminary Progress toward Removing Attention Head Superposition (link) (Chris Mathwin, Dennis Akar, Lee Sharkey). Here, Chris Mathwin studies a particular kind of attention head superposition that involves constructive and destructive interference between the outputs of different attention heads, studied by Jermyn et al. (2023). The post introduces a gated attention block, which is a type of transcoder (see Objective 2 below for further explanation) for attention blocks, that resolves this kind of attention head superposition in a toy model.
• Decomposing attention block jobs and identifying QK-circuit features with sparse transcoders (Project in progress): Keith Wynroe has been taking a different approach, using transcoders that are more similar to vanilla SAEs than Chris' gated attention blocks. In Keith's work, the features learned are in the QK circuit, and they are not trained on reconstruction of activations, but are instead trained to reconstruct the attention pattern. We use these features to construct a third-order tensor whose structure (we hope) reflects the various QK-‘jobs’ done by the attention block. Another type of sparse factorization is used on this ‘attention head jobs tensor’ to break it into (what we hope will be) individual attention block ‘jobs’. 

Better hyperparameter selection methods

Training SAEs requires selecting multiple hyperparameters. We don’t know how hyperparameters interact with each other, or how they interact with different data distributions. Thus training SAEs often involves sweeps over hyperparameters to find good combinations. Understanding the relationships between different hyperparameters (similar to Yang et al., (2022)) would let us skip expensive hyperparameter sweeps. This is especially important as we scale our interpretability methods to frontier models, where it may be prohibitively expensive to run SAE hyperparameter sweeps.

Computationally efficient sparse coding

There may be additional tips and tricks for training SAEs in more efficient ways. For instance, informed initialization schemes (such as data initialization or resampling) may improve efficiency. Or perhaps particular methods of data preprocessing might help. There is considerable room for exploration. 

On a higher level, there probably exist more efficient sparse coding methods than SAEs trained with SGD. If there are better methods, it’s important that the community not get stuck in a local optimum; we should look for these better methods.

In order to be in a position where the next objective is completable, we would need to see some progress in the above areas. Areas of progress like 'better hyperparameter selection' and 'computational efficiency' would yield quality of life improvements. Others are more important; they are essential before we can be confident in our descriptions: Areas like ‘finding functionally relevant features’ or ‘fixing feature suppression’. Other still are even more essential for progress: Unless we can decompose attention blocks in a satisfying way, we will not be able to complete the next objective, which is to fully ‘decompile networks’.

Objective 2: Decompiled networks

Once we’ve identified the functional units of a neural network, then we can decompile it by making a version of the network where superposition has been removed. In decompiled networks, the forward pass does inference in the interpretable feature basis. 

Suppose we have trained e2eSAEs in each layer and identified the functional units. We then want to identify the ‘interaction graph’ that describes how features interact between layers. This is where ‘transcoders’ come in. Transcoders, in contrast to autoencoders, are trained to produce different outputs than their inputs. To get the interaction graph between features in adjacent layers, we would train (or otherwise find, perhaps through cleverly transforming the original network's parameters into sparse feature space) a set of transcoders to produce the same output and intermediate feature activations as in the original network. The result is a sparse model that we can use for inference where we don’t need to transform our activations to the original neuron basis; the decompiled network does inference entirely in the sparse feature basis. 

Transcoders may have a variety of architectures, such as a simple matrix (as in Riggs et al., 2024 and Marks et al., 2024).  Speculatively, we may prefer using something else, such as another SAE architecture (as briefly explored in Riggs et al., 2024). Unlike a purely linear transcoder, an SAE-architecture-transcoder would be able to model nonlinear feature interactions. 

It’s worth noting that such a transcoder's sparsely activating features would be ‘interaction features’, which identify particular combinations of sparse features in one layer that activate particular combinations of sparse features in the next layer. The weights of these interaction features are the ‘interaction strengths’ between features. You can thus study the causal influence between features in adjacent layers by inspecting the weights of the transcoder, without even needing to perform causal intervention experiments. The transcoder’s interaction features thus define the ‘atomic units’ of counterfactual explanations for the conditions under which particular features in one layer would activate features in an adjacent layer.

Policy goals for network decompilation

Once we as a community get network decompilation working, we hope that it becomes a standard for developers of big models to produce decompiled versions of their networks alongside the original, 'compiled' networks. Some of the arguments for such a standard are as follows:

• Certain highly capable models will be integrated widely into society and used for economically gainful activities. This comes with some risks, which would be reduced by the existence of decompiled models that are easier to understand. 
• Developers of large models are best placed to train the decompiled versions themselves, since they have access to the training resources and infrastructure. 
• This standard would mean that, as neural networks scale, auditors and researchers would always have a version of the network that is ready for interpretation.
• It is not unreasonable for developers to internalize some of the costs associated with big models by training interpretable decompiled versions of them in addition to the base models, so that researchers can work on ensuring that the original model is safe. 
• Standardized artifacts enable standardized tests: Evaluators could, for example, run standardized tests for particular knowledge in the network, or test for signatures of dangerous cognitive capabilities, or test for particular biases. 
• Standardized artifacts enable cumulative policy development. For instance, regulators could begin designing regulations that require the networks to have particular internal properties, as identified in their decompiled networks. We might even be able to graduate from risk-management-based AI safety assurances to compliance-based AI safety assurances. 

Objective 3: Abstraction above raw decompilations

Although we expect decompiled neural networks to be much more interpretable than the original networks, we may wish to engage in further abstractions for two reasons:

1. Circuit identification: We may wish to identify ‘circuits’, i.e. modules within a neural network that span multiple layers consisting of groups of causally interacting features that activate together to serve a particular function. If we identify circuits in a principled way, then they represent a natural way to study groups of features and interactions in the network. 
2. Shorter semantic descriptions: If semantic descriptions of neural networks in terms of the lowest level features are too long, then we need to identify the right abstractions for our lowest-level objects and then describe networks one level of abstraction up. 

The best abstractions are those that reduce [mathematical or semantic] description length as much as possible while sacrificing as little [mathematical or semantic] description accuracy as possible. We previously used sparse coding for this exact purpose (see section The Unreasonable Effectiveness of SAEs for Mechanistic interpretability), so perhaps we can use them for that purpose again. So, at risk of losing all personal credibility to suggest it, SAEs may be reusable on this level of abstraction^[4]. It may be possible to train meta-SAEs to identify groups of transcoder features (which represent interactions between SAE features) that commonly activate together in different layers of the network (figure 5). The transcoder features in different layers could be concatenated together to achieve this, echoing the approach taken by Yun et al. (2021) (although they did not apply sparse coding to interactions between features in decompiled networks, only to raw activations at each layer). Going further still, it may be possible to climb to higher levels of abstraction using further sparse coding, which might describe interactions between circuits, and so on. 

Objective 4: Deep Description

So far in this agenda, we haven’t really done any (semantic) ‘interpretation’ of networks. We’ve simply decompiled the networks, putting them in a format that’s easier to interpret. Now we’re ready to start semantically describing what the different parts of the decompiled network actually do.

In mechanistic interpretability, we want a mechanistic description of all the network’s features and their interactions. On a high level, it’s important to ask what we’re actually looking for here. What is a mechanistic description of a feature?

A complete mechanistic description of a feature is ideally a description of what causes it to activate and what it subsequently does. Sometimes it makes sense to describe what a feature does in terms of which kinds of input data make it activate (e.g. feature visualization, Olah et al., 2017). Other times it makes more sense to describe what a feature does in terms of the output it tends to lead to. Other times still, it is hard or incomplete to describe things in terms of either the input or output, and instead it only makes sense to describe what a feature does in terms of other hidden features. 

There exists some previous work that aims to automate the labeling of features (e.g. Bills et al., 2023). But this work has only described neurons in terms of either the input or output of the network. These descriptions are shallow. Instead, we want deep descriptions. Deep descriptions iteratively build on shallow descriptions and bring in information about how features connect together and participate in particular circuits together. 

Early ventures into deep description have already been made, but there is potentially much, much further to go. One of these early ventures is Cammarata et al. (2021) (Curve Circuits). In this work, they used feature visualization to get a first pass of shallow descriptions of all the relevant neurons. In the next iteration of description, they showed how features in one layer get used by particular weights to construct features in the next layer; in doing so, they showed that some ‘curve features’ were not merely excited by curves in particular orientations, but also inhibited by curves in opposite orientations, thus adding more semantic detail.

This foray into deep description showed how we can use descriptions to build on each other iteratively. But these were only an initial step into deep description. This example only explained a hidden feature (a curve) in terms of features (early curves) in a previous layer; it didn’t, for instance, ‘go backward’, explaining early curves in terms of the curves they participate in. Being so early in the network, this might not be as informative an exercise as going in the forward direction. But there will exist features, particularly those toward the output of the network, where it makes more sense to go in the backwards direction, explaining hidden features in terms of their downstream causes.

What description depths might we be able to achieve if we automate the description process, and what might automating such a process look like? Here is a sketch for how we might automate deeper description. 

A sketch of an automated process for deep description: The Iterative-Forward-Backwards procedure

This procedure has three loops. Intuitively:

• The ‘Forward loop’ describes features in one layer in terms of features in earlier layers or in terms of the data. It describes what causes feature X to fire in terms of earlier features.
• The ‘Backward loop’ describes features in one layer in terms of features in later layers or in terms of the output. It describes the effects in later layers caused by feature X activating.
• The ‘Iterative loop’ lets us use the results of previous cycles to iteratively refine our descriptions based on descriptions that have previously been added, developed, or clarified.

Suppose we have a network with L layers (where layer 0 is the input data and L is the output layer) and a number of repeats for the iterative loop, R. Then, slightly more formally:

For r in (0, …, R-1):  #  The Iterative loop
	For i in(0, …, L):  #  The Forward loop
		For j in (1, …, L): 
			If i < j:
				Explain the features in layer j in terms of the (earlier) features in layer i. 
	For k in (L, …, 1):  #  The Backward loop
		For j’ in (L, …, 0): 
			If k > j’:
				Explain the features in layer j’ in terms of the (later) features in layer k.

When we say ‘Explain feature X in terms of features Y’, we’re leaving a lot undefined. This step is doing a lot of work. It may take several forms. For instance:

• It potentially involves looking at the max activating samples of feature X. If Y is the data, then we’d look at the data and which data caused X to activate a lot. But note that Y may be hidden features too. 
• It could involve testing hypotheses about our descriptions of features X in terms of Y. For example, we could look at the features X and the weights that connect features Y to them and make predictions about the activations of features Y that would cause features X to activate as in Bills et al. (2023).
• It could involve predicting the outcomes of particular causal interventions on features, as in causal scrubbing. 

To add to the intuitions of what this procedure is doing, it is helpful to describe previous interpretability methods in terms of it (Figure 6):

• Feature visualization-based methods (e.g. activation atlases or max-activating dataset-examples) are instances of one part of the forward loop, where layer l is explained in terms of layer 0 (the input layer).
• The logit lens is an instance of one part of the backwards loop, where features in hidden layer j’ are explained in terms of the output it corresponds to.
• The low level explanations of curve circuits in Cammarata et al. (2021) are instances of one step of the forward loop, where hidden layer features are explained in terms of earlier hidden layer features. This occurs during the first iterative loop, since the explanations for each feature are simply given only in terms of layer 0 (the input data). Subsequent iterative loops would be able to make use of much more information.

I expect the procedure that we end up doing to look substantially different from this (and include a lot more detail). But this sketch is merely supposed to point toward algorithms that could let us automate a lot of semantic description in interpretability. 

Objective 5: Mechanistic interpretability-based evals & other applications of mechanistic interpretability

If we figure out how to automate deep description of decompiled networks, then we’ll have satisfactory mechanistic interpretability. This could be used for a number of applications, including: 

• Mechanistic interpretability-based model evaluations: We can develop red-teaming procedures and benchmarks based on our mechanistic interpretability methods to assess the safety and ethics of the models’ internal representations and learned algorithms. These would be a type of ‘understanding-based model evals’. Not only could these evals permit new kinds of model capability evals, they may also permit more general alignment evals, where we can make good predictions of how models would behave on a much wider range of circumstances than current behavioral model evals. 
  
  We think of mech-interp based model evaluations as falling into two broad categories:
  • Mechanistic interpretability-based model red teaming: Red-teaming AI models involves trying to find inputs that fail some safety- or security-based test. Currently, most red-teaming involves searching through input-space (or latent space) to find inputs (or potential inputs) that lead to concerning outputs (e.g. Perez et al., 2022). Mechinterp-based evals can aim to do better in a couple of ways: 
    • 1) Mechanistic interpretability-based evals could try to find inputs that lead to concerning combinations of features. For example, we could try to find inputs that elicit deception that we wouldn’t have been able to detect using behavioral tests alone; 
    • 2) Mechanistic interpretability-based evals don’t have to look for inputs that cause concerning hidden feature activations or outputs (which may be difficult to enumerate for large networks). We can find (earlier) hidden features that activate concerning (later) hidden features or outputs. We could subsequently use these earlier hidden features to find even earlier hidden features that cause concerning behavior. This might even let us work backwards from hidden features, potentially using this approach as a tool to find inputs that lead to concerning behavior.
  • Mechanistic interpretability-based model benchmarking: Behavioral benchmarks are standardized sets of tests where, given a certain input, the output of a model is evaluated. If it’s the ‘right’ kind of output (according to some evaluation criteria), then the model does well on the benchmark. In mechanistic interpretability-based benchmarks, instead of assessing outputs, we assess internal activations. We’d similarly use some evaluation criteria to determine whether the input caused the ‘right’ kind of internal activations to occur.
• Alignment method evaluations: When we have mechanistic interpretability-based model evaluations to assess model’s safety properties, we would then be able to better compare the strengths and weaknesses of different alignment methods. We may be able to strengthen different approaches by using mechinterp-based model evals to, e.g. identify key gaps in the finetuning data that lead to failures of alignment.
• Targeted interventions on models: When we understand how models work, it seems likely that we can use this information to make targeted interventions on models. For instance, we may be able to:
  • Accurately ablate specific pieces of knowledge (e.g. for anonymization purposes or for removing unsafe capabilities); 
  • Whitelist only a small set of capabilities, giving us better guarantees about how models will behave on specific distributions; 
  • Make better probes that use features (i.e. causal components of the network’s internal mechanisms) rather than probes identified using correlations on a training dataset; or
  • Identify better steering vectors for activation steering, thus affording us more control over model behavior.
• Capability prediction: One of the problems with behavioral evals is that just because we can’t get a model to behave badly or exhibit a certain capability, doesn’t mean there don’t exist ways to get it to do so; we just haven’t found them yet. In other words, ‘Absence of evidence is not evidence of absence’. Mechinterp-based evals might alleviate this problem by providing us with a way to predict capabilities and more convincingly determine whether systems can plausibly exhibit dangerous behaviors under some circumstances. For instance, if we observe that a model has all the requisite representations for particular cyber offensive capabilities, we could predict that there might exist some contexts where the model would use those capabilities even though we haven’t yet identified a way to elicit them. 
• Mechanistic interpretability during training: One of the barriers to doing many mechinterp-based evals during training is that it first involves interpreting a snapshot of the model. By default, this might be too expensive to do with high frequency. Nevertheless, we’d like to be able to do interpretability during training in order to e.g. better catch misalignment or dangerous capabilities before risks are realized, or to forecast discontinuities in training. We would therefore like to do mechanistic interpretability as frequently as possible. We will need efficient mechanistic interpretability methods to do this. In the long term, a potential approach might be ‘stateful interpretability’, where e.g. our semantic descriptions of features and interactions are stored as embedding vectors (a ‘state’) and, conditioned on a gradient update of the model being trained, we use another model to incrementally update the interpretation embeddings alongside the model updates. 
• Robust-to-training mechanistic interpretability: Once we have sufficiently good and sufficiently cheap mechanistic interpretability, one possible use is to 'train models against the interpretability methods'. For example, if we identify features or circuits that we don’t like, we could design loss functions (or other feedback functions) that penalize the network for having them. One risk is that our interpretability methods are not ‘robust to training’ against them (Hubinger et al., 2022), so networks might simply learn to represent the features or circuits in some other, uninterpretable way (Sharkey, 2022). It remains an open question whether future interpretability methods will be robust enough for this. This debate can probably be resolved empirically before its potential use in highly capable, potentially deceptive models. 

I think AI safety would be in a pretty great place if we achieved these objectives. And, to me, most feel within reach - even on reasonably short timelines - though not for a single researcher or even a single research team. It will require a concentrated research program and an ecosystem of researchers. I hope some of them will find this roadmap useful. I plan to work on it over the next few years, although some deviations are inevitable. And if others are interested in collaborating on parts of it, I'd love to hear from you! Send me a message or join the #sparse-autoencoders channel on the Open Source Mechanistic Interpretability Slack workspace. 


Acknowledgements: I'm very grateful for helpful discussions and useful feedback and comments on previous drafts, which greatly improved the quality of this post, from Marius Hobbhahn, Daniel Braun, Lucius Bushnaq, Stefan Heimersheim, Jérémy Scheurer, Jordan Taylor, Jake Mendel, and Nix Goldowsky-Dill.
 

1. ^{^}

   The analogy between mechanistic interpretability and software reverse engineering

   Mechanistic interpretability has been compared to software reverse engineering, where you start with a compiled program binary and try to reconstruct the software’s source code. The analogy is that a neural network is a program that we have to decompile and reverse engineer. On a high level, software reverse engineering comprises three steps, which (not coincidentally) neatly map onto the three steps of mechanistic interpretability: 
   

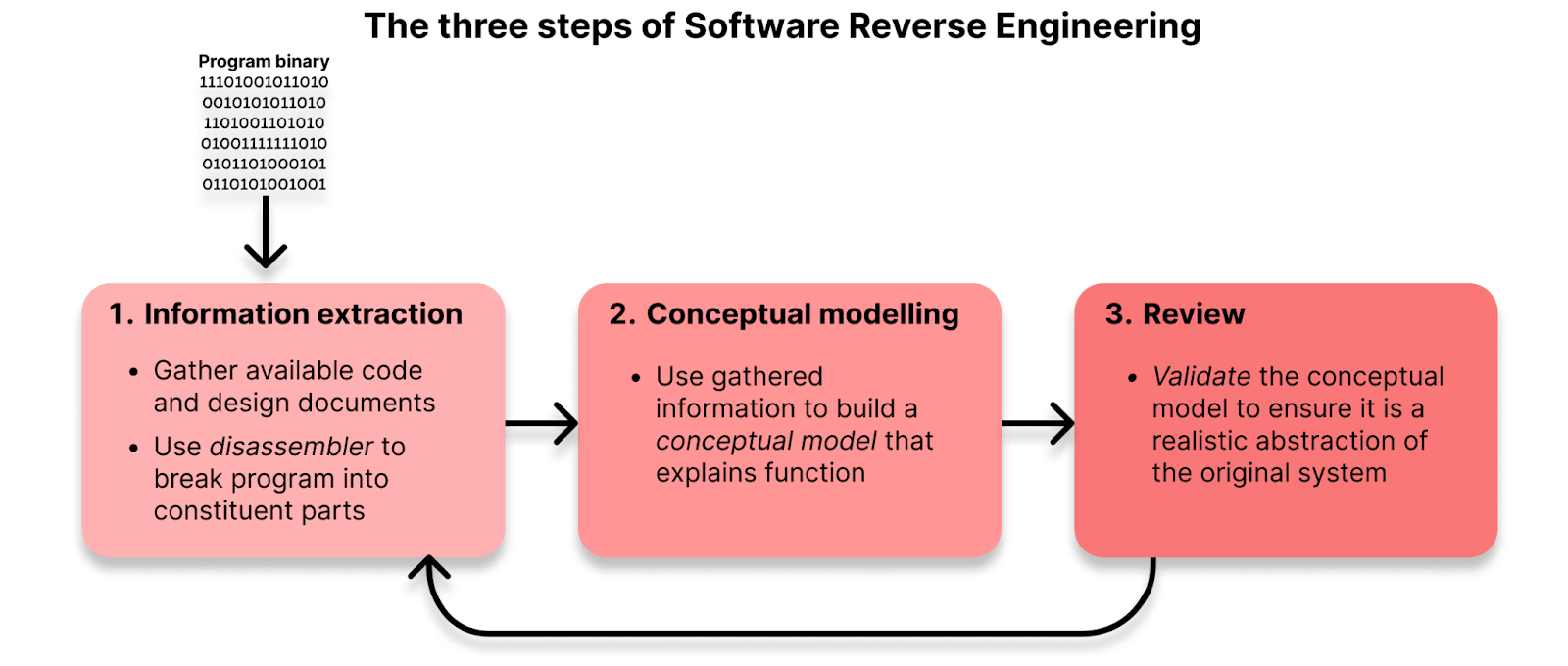
   The three steps of Software Reverse engineering

   1) Information extraction: In the first step, you gather what information you can that might help you understand what the program is doing. It might involve the use of a ‘disassembler’, breaks the program into its constituent parts by converting binary code into assembly code or converting machine language into a user friendly format (source). Or it may involve gathering other information such as design documents.

   2) Conceptual modeling: Using the gathered information, create a conceptual model of what the program is doing. Software reverse engineering may implement this conceptual model in code that they write themselves or as a flow diagram. 

   3) Review: Then the conceptual model is validated to check how well it explains the original program. If it performs well, then there’s no need to keep going. If it performs poorly, then either new information will need to be extracted and/or a new conceptual model built. 

2. ^{^}

   To the best of my understanding, ARC's work on heuristic arguments could be described as aiming to formalize semantic description. This seems like a very good idea.

3. ^{^}

   Previous interpretability research that aimed to use polytopes as the unit of explanation(Black et al., 2022) grouped polytopes using clustering methods, which, unlike SAEs, offer no way to ‘factorize’ a network’s function into compositional components. This yielded too long mathematical descriptions. However, it may be possible to group polytopes using other methods that are more compositional than clustering.

4. ^{^}

   Although meta-SAEs might be useful here, it may not be advisable to use them. The inputs to meta-SAEs may become too wide for computational tractability, for instance. Alternatively, there may simply be better tools available: Meta-SAEs are solving a slightly different optimization problem compared with base/feature-level SAEs; on the base level, they’re solving a sparse optimization problem (where we’re looking for sparsely activating features in neural activations); on the meta-SAE level, it’s a doubly sparse optimization problem (where we’re looking for sparsely activating combinations of sparse feature activations). It’s plausible that other unsupervised methods are better suited to this task.