“Money is a machine whose function is to do quickly and conveniently what would be done, though less quickly and conveniently, without it” — J.S Mill
 

♥ An Introduction to an Ignored Problem:

It is quite common that in undergraduate economics course, particularly in Money and Banking, students are taught that money is adequately defined as a means of general exchange between economic agents and that it is an institution created for the purpose of eliminating the inconveniences of barter.

However, the student rarely asks himself the reason for this, much less observes that the logic given to him is wrong. What does it ultimately mean for currency to be a general medium of exchange? And why is barter a less desirable option than indirect exchange using money?

When justifying their argument about the superiority of monetary transactions over barter, professors usually talk about a problem called “double coincidence of wants”. This problem supposedly inherent to barter develops as follows: In an economy without money, people would have to transact goods of equal value. I produce apples and you produce oranges, so if I want your oranges I simply exchange with you an equivalent of apples for an equivalent of oranges. The problem arises when, due to variations in subjective valuations, you interpret that my number of apples is not worth your number of oranges. A divergence occurs between my desire for your oranges and your desire for my apples. In this case, I would not be able to transact with you and I would not get the goods I want, creating an inefficient situation from a Paretian point of view^[1].

With money this problem would be solved, as it is a good accepted by all market agents in exchange for their production. Thus, it is a general mean of exchange (valued) by all market agents. With it, I can exchange my apple production for a money equivalent and then exchange my currency equivalent for its orange production. The trade-offs are satisfied and we then have a Pareto-efficient situation.

However, the economic logic is much more complex when looked at in depth.

The “double coincidence of wants” argument was originally introduced by the English economist William S. Jevons (1835 - 1882) in his 1875 treatise “Money and the Mechanism of Exchange”. Jevons noted that in a barter economy not only could a divergence between agents' preferences happens, but also that a highly inefficient complexity would arise in relation to “exchange rates” between different goods. Each good and service would have to be priced in terms of all other goods according to a rule of three that realized the proportion of how much of a given good would be worth in terms of the other goods. We can represent this rule as follows:
 

                                                               $(P\left(n\right)=\frac{N(N-1)}{2})$

Where P(n) is the quantity of prices in a barter economy and N is the number of goods and services in that economy. Thus, in an economy that has 100 goods, for example, there would be a total of 4950 prices or “exchange rates” between one good and the others. According to Jevons, the problem of adjusting each commodity, often indivisible, to its exchange rates could be avoided by choosing a common medium of exchange that unifies all exchange rates, such as a commodity that takes on the role of money^[2].

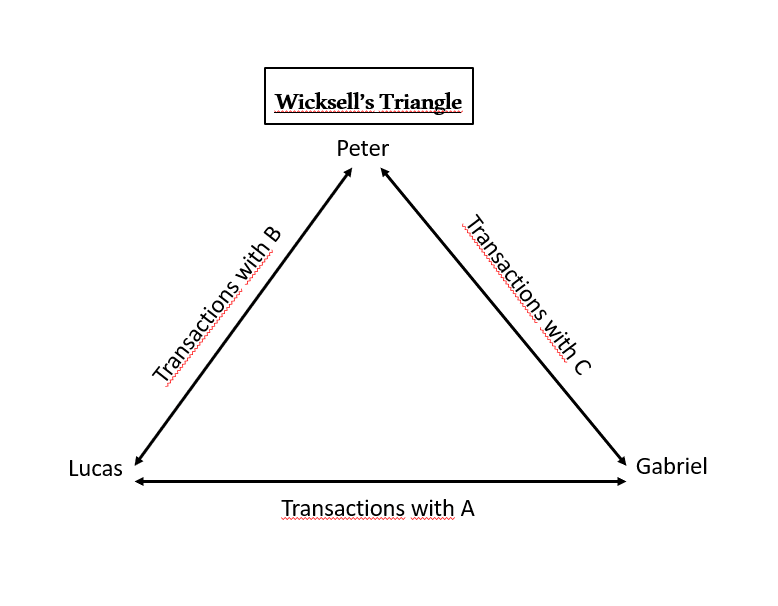
Despite the sophisticated logic used by Jevons, it has a limitation. Note, dear reader, that Jevons and your undergraduate professor talk about a scenario where there are only two people transacting their productions. But what happens when we introduce a third person and a third commodity into our hypothetical scenario? What Swedish economist Knut Wicksell (1851 - 1926) observed in doing so is that the double coincidence of desires argument does not hold.

Imagine an economy where there are three people: Peter, Lucas and Gabriel. Each of these people has a capital good or productive factor that allows them to produce different goods. Pedro produces A, Lucas produces B and Gabriel produces C. Even though each individual likes what they produce, they have superior preferences for the goods of other market participants. Pedro wants Lucas's goods, Lucas wants Gabriel's goods, and Gabriel wants Pedro's goods. In this scenario, efficiency cannot be achieved through bilateral exchange gains, but only through multilateral gains; that is, the optimal allocation of resources will only be established when the individuals in question establish a circular flow of exchange. The shape of this exchange is known as the Wicksell Triangle:


If the parties have aligned preferences and trust each other, then, after meeting for some initial period of time, they exchange their assets and the optimal allocation is reached. But what would happen if individuals didn't trust each other? This situation could be resolved by creating legal obligations (rights) over each other's production. Assuming that the enforcement of property rights is perfect, this would mean that individuals could transact without fear of opportunism. But what if they had unaligned preferences? What would happen if Gabriel did not want Lucas's products in exchange for his produce and Lucas did not accept Pedro's goods? In this case, the circular flow would be broken and the economy would return to a pareto-inefficient situation^[3]. But is this really necessary?

What Wicksell observed is that such a situation can be resolved if individuals arbitrate between their productions. Pedro may not wish to accept the property rights over Gabriel's production C for his own consumption, but he can perfectly retain C to then exchange with Lucas for his production B; production that he values. Thus, by carrying out arbitration between goods, individuals are able to maintain an efficient exchange economy even with barter and without the existence of a currency; given that property titles over production are mere legal representations of fractions of individuals' real production and not a separate commodity used as a general means of exchange. Goods A, B and C (or their title deeds) are all at the same time means of exchange^[4].

This is a scalable conclusion. The more people, the less likely a problem of double coincidence of desires will occur. Thus, an economy without currency can be theoretically efficient.

♠ The Walrasian Medium of Exchange Problem:

Wicksell's conclusion may seem strange at first glance, but it is just a development of monetary thinking within the general equilibrium perspective. The notion that any commodity could be used as a medium of exchange and that a general medium of exchange would not be necessary for efficient allocation was originally expounded by the great French mathematician Leon Walras (1834 - 1910).
 

Walras' reasoning is quite simple. The moment a society or group of individuals chooses to use a certain commodity X as a means of exchange, an economic choice problem arises. The total available quantity amount of X for consumption decreases, due to it being simultaneously used as a medium of exchange, this is equivalent to a scenario where the supply of X for consumption is reduced. Since there is less quantity supplied in the market, the relative price of X in relation to other goods increases; which is equivalent to saying that the prices of all goods are deflated in relation to the price of division between quantity of consumption, Qx, and quantity of medium of exchange, Mx, such that there is a relationship or coefficient of choice between the total of X and the quantity variables as follows:
                                                                                                                                                                                                                         $(Qx+Mx=nQt)$

Where n is the relationship between the total of X and the chosen quantity of X to be a medium of exchange. Rearranging the equation we have:

                                                           $(\frac{Qx}{n}+\frac{Mx}{n}=Qt)$

However, it is worth remembering that the amount of medium of exchange necessary to maintain the flow of exchange depends on the price and quantities of other goods that agents wish to consume, in such a way that:

                                            $(Mx=Qx+QyPy+QzPz...)$

Considering that Mx has to be given considering its relationship with the total quantity, we have that:

                                                    $(\frac{Mx}{n}=\frac{QyPy}{n}+\frac{QzPz}{n}...)$

From this relationship we draw that there is such an equivalence between the quantity of medium of exchange and the quantity of goods that would be purchased with the currency and the quantity of X for consumption that an automatic regulation of the quantity of medium of exchange would occur by n. If the quantity of currency is greater than the balance between supply and demand, then Mx would be transformed back into a commodity for consumption while the quantity for consumption had more value than the quantity for the medium of exchange (inflation process) until the price equilibrium between the two was once again established.

Following Walras' logic, money would not be strictly necessary. People could simply adopt means of exchange as needed and, following the reasoning later developed in the Wicksell Triangle, reach an efficient balance. In Walras's thinking there is no argument for why one commodity is adopted as a means of general exchange and another is not. It is simply meaningless to choose a currency. For this reason, the thinking of Walras and Wicksell favors the use of the cheapest possible means of exchange. Using something like gold as a medium of exchange would be inefficient, given that its value for consumption is higher than for a medium of exchange, for example. It is much more rational to use cheaper means of exchange, such as pieces of painted paper. 

♦ The Problem of Transaction Costs and the Rationality of Money:

Although the logic elaborated by Walras and Wicksell makes sense, it leads to absurd conclusions and does not address certain problems that lead to a rational choice to adopt a currency.

The American economist Robert Clower (1926 - 2011) observed that in a world governed by the logic presented by Walras there would be a situation where individuals would maximize utility according to the following restrinction^[5]:

                                          ${\sum }_{i=1}^{n}Pi=(diJ-SiJ)+Mj-M{j}^{\prime }$

Where diJ represents a desired quantity of goods, SiJ represents the initial quantity of goods, Mj is the initial quantity of medium of exchange, Mj' is the desired quantity and Pi is a price index in terms of the medium of exchange P1,…Pn . What this model ends up postulating is that any change in the quantity of goods or the quantity of medium of exchange will have exactly the same effect; given that both are mutually adjustable. That is, even if Mj' = 0 for all but one individual, this does not imply that individuals in this economy will have no influence on demand, since SiJ enters the restriction equation in the same way as Mj', so that the real goods of the economy would be indistinguishable from the quantities used as a medium of exchange and both would be sources of excess demand in markets. Thus, the conclusion of the Walrasian model is that the increase in the supply of goods has an inflationary effect; which is absurd in face of economic data and experience. 

What Clower will show is that there must be a commodity chosen as a general medium of exchange that serves as a source of excess demand in the markets. Therefore, there must be money. But why should there be a currency? Clower's argument does not provide us with an explanation of why currencies exist in opposition to the Walrasian argument, only that it has absurd conclusions from a macroeconomic point of view.

The person who would provide a rational choice explanation for the existence of money would be Clower's colleague at UCLA, the brilliant economist Armen Alchian (1914 - 2013). Alchian would demonstrate that money exists primarily as an institution that reduces transaction costs, particularly the information cost involved in looking for people to transact with in terms of the medium of exchange.

Consider the simple direct exchange model of the Wicksell Triangle where there are three goods A, B and C. In a situation where goods are exchanged directly, the resource limitation in such an economy can be analytically expressed by:

                                                            $\mathrm{0...},-\mathrm{1...},\mathrm{1...}$
 

Where 0 represents an initial moment where everyone has an initial endowment of goods, -1 represents the moment where the individual exchanges his commodity for a medium of exchange type commodity and 1 is the moment where he exchanges this medium of exchange for another commodity. that it values at a price at least equal to that of the initial commodity. The Walrasian question in such a situation would be: Why would such an exchange equilibrium be less preferable than an exchange equilibrium where a commodity acts as a general medium of exchange?

Suppose that Cab and Cac are the costs of exchanging A for B and A for C respectively. Such costs, naturally, are compounded due to the binary characteristic of buying and selling involved in the circular flow, so that:

                                                         $Cab={Ca}^v+{Cb}^c$
                                                         \(Cac\ =\ {\rm Ca}^v\ +\ {\rm Cc}^c\\)

Where Cv is the selling cost and Cc is the purchasing cost. This decomposition leads us to the counterintuitive conclusion that logically:

\(Cac\ <\ Cab\ +\ Cac\ =\ {\rm Ca}^v\ +\ {\rm Cc}^c\ <\ {\rm Ca}^v\ +\ {\rm Cb}^c\ +\ {\rm Cb}^v\ +\ {\rm Cc}^c\\)

Therefore, Walras and Wicksell are right when they say that it makes no sense to argue that a currency should arise from considerations of the costs of buying and selling in exchange relationships between individuals. However, this changes when we analyze the issue from the perspective of transaction costs. To do this, we will consider that P is the probability of an individual wanting to exchange a commodity (be it A, B or C) and that, naturally, there is no correlation in the desires of what the individual intends to buy and what he intends to sell. So, let's say, Pa and Pb could express the probabilities of an individual wanting to exchange A for B. In an exchange economy, a merchant who wants to exchange A for B will have to make a series of encounters such that the number of attempts he will have to do:

                                                                         \(\frac{1}{PaPb}\\)

In other words, the number of people who really want to exchange A for B. A person who exchanges in an economy of intermediate exchanges using a general means of exchange will have their number of attempts defined by:

                                                                \(\ \frac{1}{PaPb}\ +\ \frac{1}{PbPc}\ \\)

In such a way that we logically conclude that:

                                                        $\frac{1}{PaPb}>\frac{1}{PaPb}+\frac{1}{PbPc}$

Since Pb > Pa + Pc

In other words, an economy of exchange using currency (general medium of exchange) will be preferable to one of direct exchange as long as the intermediate commodity is better at reducing information costs than other commodities.

In abstract terms: A commodity X will be chosen as the general medium of exchange since X = max(Pb).

 

BIBLIOGRAPHY:

— WICKSELL, Knut. Lessons in Political Economy. Abril Cultural, São Paulo, 1985;

— WALRAS, Leon. Compendium of the Elements of Pure Political Economy. Abril Cultural, São Paulo, 1985;

— CLOWER, Robert. A Reconsideration of the Microfoundations of Monetary Theory. Economic Inquiry, vol. 6, no. 1, p. 1-8, 1967;

— ALCHIAN, Armen A. Why Money?. Journal of Money, Credit and Banking, vol. 9, no. 1, p. 133-140, 1977;

—OSTROY, Joseph M.; STARR, Ross M. The Transactions Role of Money. Handbook of monetary economics, vol. 1, p. 3-62, 1990.

1. ^{^}

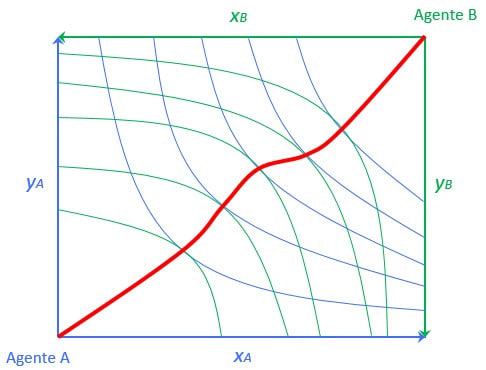
   The smart student will quickly connect the previous explanation with the Edgeworth Box:
   
    

2. ^{^}

   The same logic applies to explain why, despite having flexible exchange rate regimes, most countries in the world use a reference currency (the US Dollar) when carrying out international transactions.

3. ^{^}

   My colleague Jean Brückener made the observation that this scenario would be maintained or even worsened if we introduced time variation between exchanges. What if agents exchanged their assets in installments? There would be a problem of intertemporal divergence of preferences and, since real interest is given as a function of this intertemporal exchange of real goods, there would also be a distortion in the price of time in this economy. Although the observations make sense, time variation is explicitly disregarded in Wicksell's analyzes and I ended up not going into this dimension of the problem.

4. ^{^}

   The smart student will observe that this is the exchange mechanism implicit in the Arrow-Debreu General Equilibrium Model

5. ^{^}

   Assuming that: $\left(MaxU(d1J,\dots .,dnJ,Mj/P)\right)$