(This is a follow up to Anthropic's prior work on Toy Models of Superposition.)
The authors study how neural networks interpolate between memorization and generalization in the "ReLU Output" toy model from the first toy model paper:
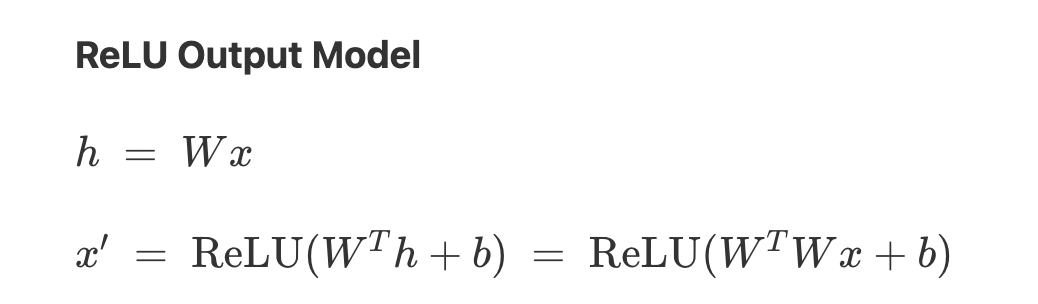
They train models to perform a synthetic regression task with training points, for models with hidden dimensions.
First, they find that for small training sets, while the features are messy, the training set hidden vectors (the projection of the input datapoints into the hidden space) often show clean structures:
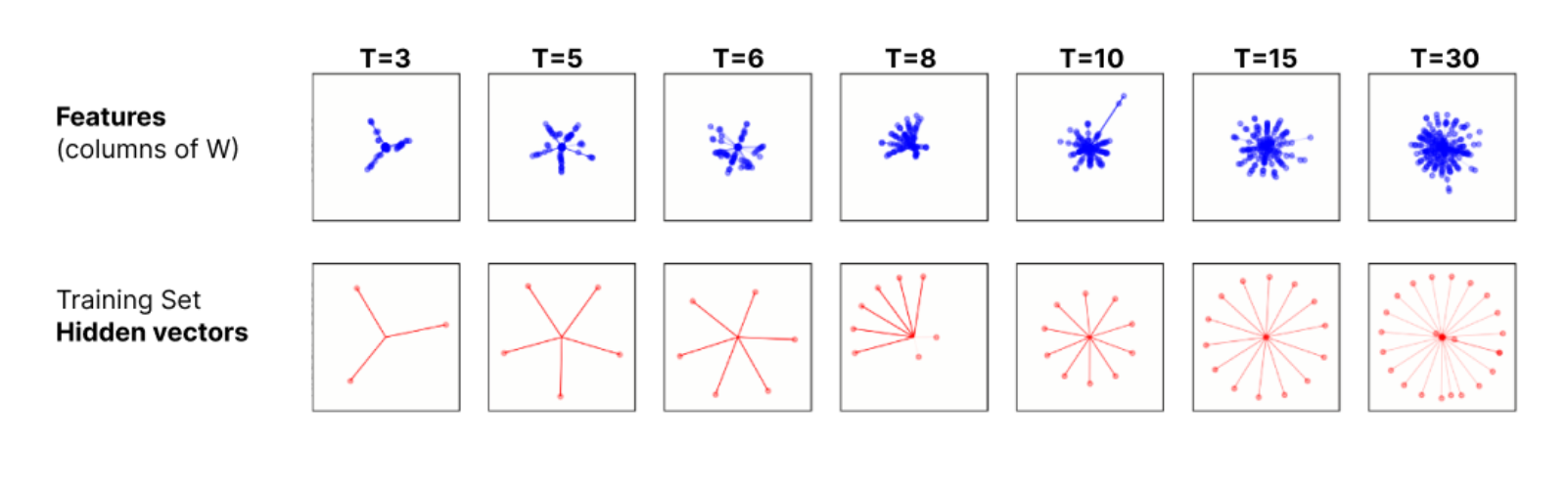
They then extend their old definition of feature dimensionality to measure the dimensionalities allocated to each of the training examples:
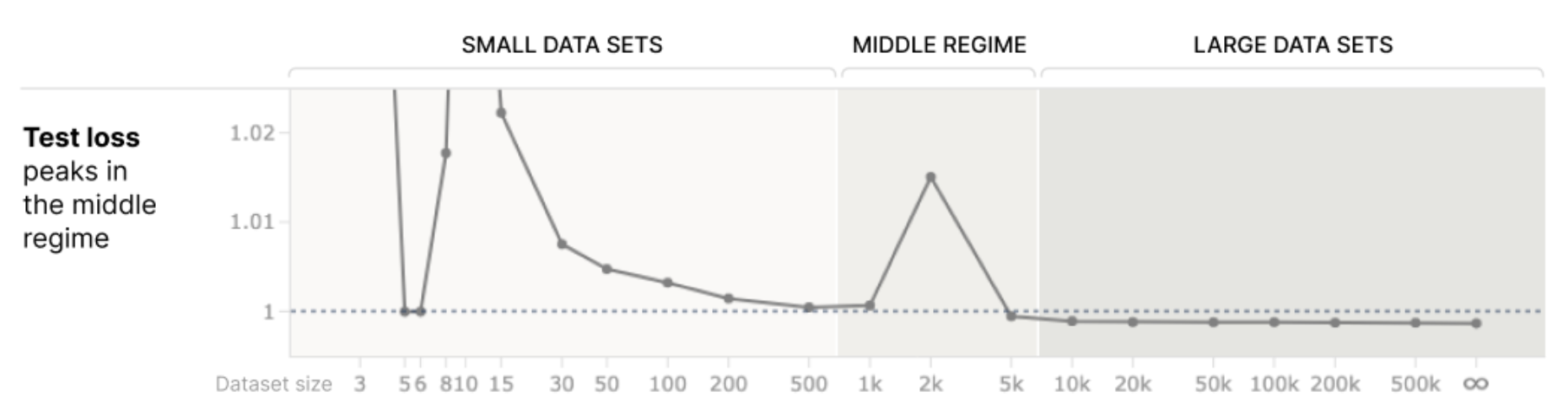
and plot this against the data set size (and also test loss):
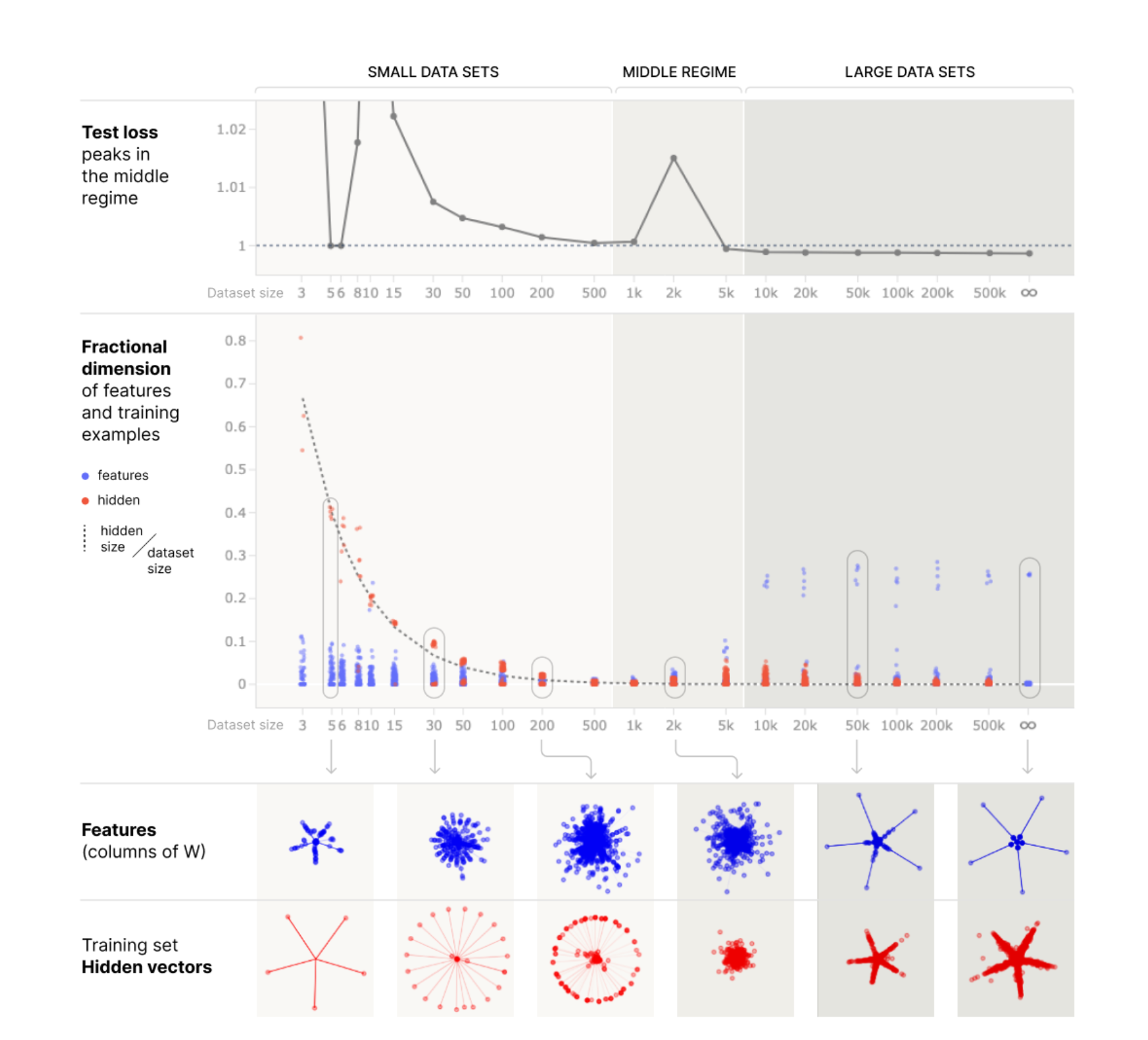
This shows that as you increase the amount of data, you go from a regime with high dimensionality allocated to training vectors and low dimensionality allocated to features, to one where the opposite is true. In between the two, both feature and hidden vector dimensionalities receive low dimensionality, which coincides with an increase in test loss, which they compare to the phenomena of "data double descent" (where as you increase data on overparameterized models with small amounts of regularization, test loss can go up before it goes down).
Finally, they visualize how varying and affects test loss, and find double descent along both dimensions:
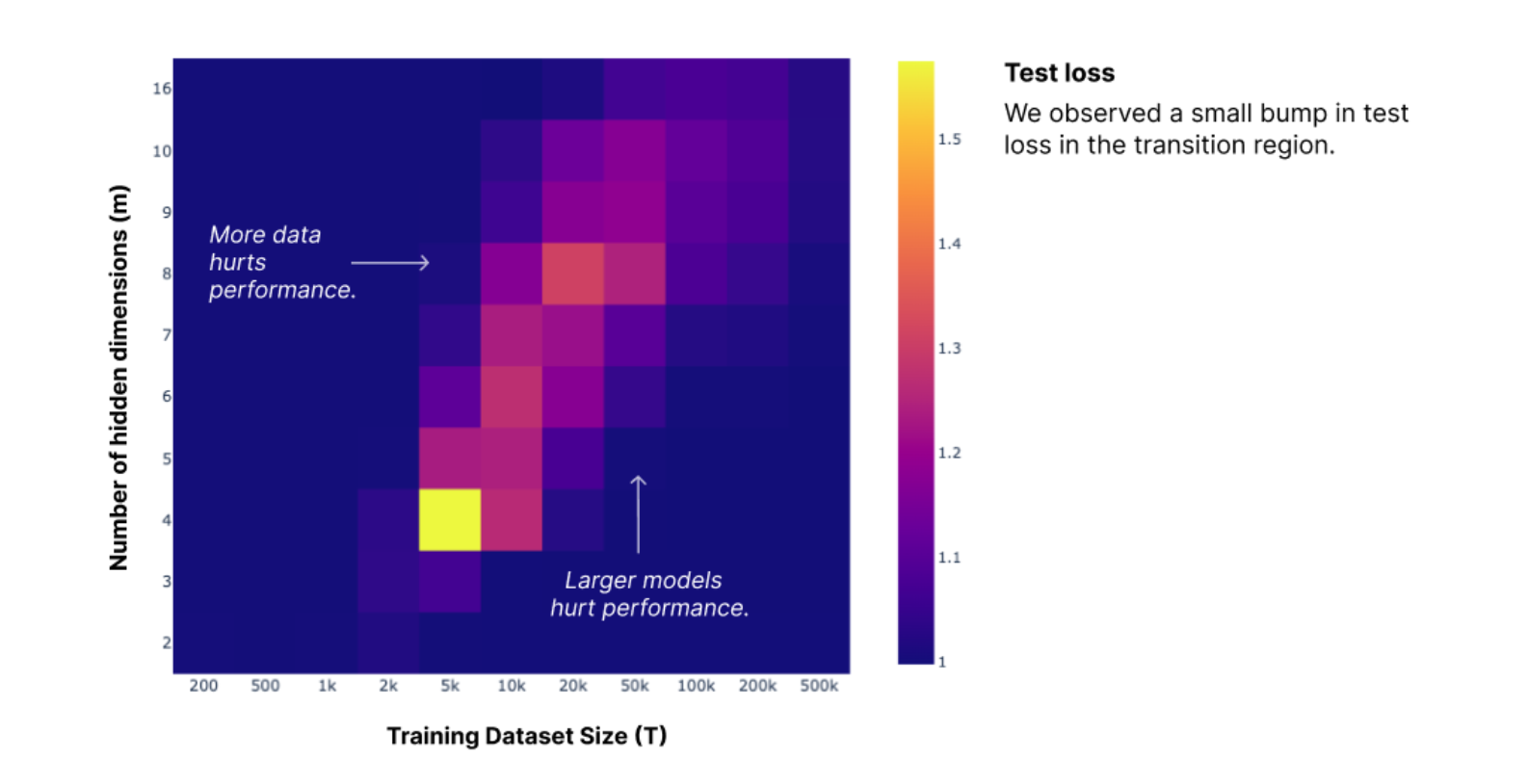
They also included some (imo very interesting) experiments from Adam Jermyn, 1) replicating the results, 2) exploring how weight decay interacts with this double descent-like phenomenon, and 3) studying what happens if you repeat particular datapoints.
Some limitations of the work, based on my first read through:
- The authors note that the results seem quite sensitive to hyperparameters, especially for low hidden dimension . For example, Adam Jermyn's results differ from the Anthropic Interp team results (though the figures still look qualitatively similar).
- I'm still not super convinced how much results from the superposition work apply in practice. I'd be interested in seeing more work along the lines of the MNIST preliminary experiment done by Chris Olah at the bottom.
(I'll probably have more thoughts as I think for longer.)

This is a good summary of our results, but just to try to express a bit more clearly why you might care...
I think there are presently two striking facts about overfitting and mechanistic interpretability:
(1) The successes of mechanistic interpretability have thus far tended to focus on circuits which seem to describe clean, generalizing algorithms which one might think of as the "non-overfitting parts of neural networks". We don't really know what "overfitting mechanistically is", and you could imagine a world where it's so fundamentally messy we just can't understand it!
(2) There's evidence that more overfit neural networks are harder to understand.
A pessimistic interpretation of this could be something like: Overfitting is fundamentally a messy kind of computation we won't ever cleanly understand. We're dealing with pathological models/circuits, and if we want to understand neural networks, we need to create non-overfit models.
In the case of vision, that might seem kind of sad but not horrible: you could imagine creating larger and larger datasets that reduce overfitting. ImageNet models are more interpretable than MNIST ones and perhaps that's why. But language models seem like they morally should memorize some data points. Language models should recite the US constitution and Shakespeare and the Bible. So we'd really like to be able to understand what's going on.
The naive mechanistic hypothesis for memorization/overfitting is to create features, represented by neurons, which correspond to particular data points. But there's a number of problems with this:
The obvious response to that is "perhaps it's occurring in superposition."
So how does this relate to our paper?
Firstly, we have an example of overfitting -- in a problem which wasn't specifically tuned for overfitting / memorization -- which from a naive perspective looks horribly messy and complicated but turns out to be very simple and clean. Although it's a toy problem, that's very promising!
Secondly, what we observe is exactly the naive hypothesis + superposition. And in retrospect this makes a lot of sense! Memorization is the ideal case for something like superposition. Definitionally, a single data point feature is the most sparse possible feature you can have.
Thirdly, Adam Jermyn's extension to repeated data shows that "single data point features" and "generalizing features" can co-occur.
The nice double descent phase change is really just the cherry on the cake. The important thing is having these two regimes where we represent data points vs features.
There's one other reason you might care about this: it potentially has bearing on mechanistic anomaly detection.
Perhaps the clearest example of this is Adam Jermyn's follow up with repeated data. Here, we have a model with both "normal mechanisms" and "hard coded special cases which rarely activate". And distinguishing them would be very hard if one didn't understand the superposition structure!
Our experiment with extending this to MNIST, although obviously also very much a toy problem, might be interpreted as detecting "memorized training data points" which the model does not use its normal generalizing machinery for, but instead has hard coded special cases. This is a kind of mechanistic anomaly detection, albeit within the training set. (But I kind of think that alarming machinery must form somewhere on the training set.)
One nice thing about these examples is that they start to give a concrete picture of what mechanistic anomaly detection might look like. Of course, I don't mean to suggest that all anomalies would look like this. But as someone who really values concrete examples, I find this useful in my thinking.
These results also suggest that if superposition is widespread, mechanistic anomaly detection will require solving superposition. My present guess (although very uncertain) is that superposition is the hardest problem in mechanistic interpretability. So this makes me think that anomaly detection likely isn't a significantly easier problem than mechanistic interpretability as a whole.
All of these thoughts are very uncertain of course.
Super interesting, thanks! I hadn't come across that work before, and that's a cute and elegant definition.
To me, it's natural to extend this to specific substrings in the document? I believe that models are trained with documents chopped up and concatenated to fit into segment that fully fit the context window, so it feels odd to talk about document as the unit of analysis. And in some sense a 1000 token document is actually 1000 sub-tasks of predicting token k given the prefix up to token k-1, each of which can be memorised.
Maybe we should just not apply a gradient update to the tokens in the repeated substring? But keep the document in and measure loss on the rest.