This is a good summary of our results, but just to try to express a bit more clearly why you might care...
I think there are presently two striking facts about overfitting and mechanistic interpretability:
(1) The successes of mechanistic interpretability have thus far tended to focus on circuits which seem to describe clean, generalizing algorithms which one might think of as the "non-overfitting parts of neural networks". We don't really know what "overfitting mechanistically is", and you could imagine a world where it's so fundamentally messy we just can't understand it!
(2) There's evidence that more overfit neural networks are harder to understand.
A pessimistic interpretation of this could be something like: Overfitting is fundamentally a messy kind of computation we won't ever cleanly understand. We're dealing with pathological models/circuits, and if we want to understand neural networks, we need to create non-overfit models.
In the case of vision, that might seem kind of sad but not horrible: you could imagine creating larger and larger datasets that reduce overfitting. ImageNet models are more interpretable than MNIST ones and perhaps that's why. But language models seem like they morally should memorize some data points. Language models should recite the US constitution and Shakespeare and the Bible. So we'd really like to be able to understand what's going on.
The naive mechanistic hypothesis for memorization/overfitting is to create features, represented by neurons, which correspond to particular data points. But there's a number of problems with this:
- It seems incredibly inefficient to have neurons represent data points. You probably want to memorize lots of data points once you start overfitting!
- We don't seem to observe neurons that do this -- wouldn't it be obvious if they existed?
The obvious response to that is "perhaps it's occurring in superposition."
So how does this relate to our paper?
Firstly, we have an example of overfitting -- in a problem which wasn't specifically tuned for overfitting / memorization -- which from a naive perspective looks horribly messy and complicated but turns out to be very simple and clean. Although it's a toy problem, that's very promising!
Secondly, what we observe is exactly the naive hypothesis + superposition. And in retrospect this makes a lot of sense! Memorization is the ideal case for something like superposition. Definitionally, a single data point feature is the most sparse possible feature you can have.
Thirdly, Adam Jermyn's extension to repeated data shows that "single data point features" and "generalizing features" can co-occur.
The nice double descent phase change is really just the cherry on the cake. The important thing is having these two regimes where we represent data points vs features.
There's one other reason you might care about this: it potentially has bearing on mechanistic anomaly detection.
Perhaps the clearest example of this is Adam Jermyn's follow up with repeated data. Here, we have a model with both "normal mechanisms" and "hard coded special cases which rarely activate". And distinguishing them would be very hard if one didn't understand the superposition structure!
Our experiment with extending this to MNIST, although obviously also very much a toy problem, might be interpreted as detecting "memorized training data points" which the model does not use its normal generalizing machinery for, but instead has hard coded special cases. This is a kind of mechanistic anomaly detection, albeit within the training set. (But I kind of think that alarming machinery must form somewhere on the training set.)
One nice thing about these examples is that they start to give a concrete picture of what mechanistic anomaly detection might look like. Of course, I don't mean to suggest that all anomalies would look like this. But as someone who really values concrete examples, I find this useful in my thinking.
These results also suggest that if superposition is widespread, mechanistic anomaly detection will require solving superposition. My present guess (although very uncertain) is that superposition is the hardest problem in mechanistic interpretability. So this makes me think that anomaly detection likely isn't a significantly easier problem than mechanistic interpretability as a whole.
All of these thoughts are very uncertain of course.
Interesting context, thanks for writing it up!
But language models seem like they morally should memorize some data points. Language models should recite the US constitution and Shakespeare and the Bible
I'm curious how you'd define memorisation? To me, I'd actually count this as the model learning features - a bunch of examples will contain the Bible verse as a substring, and so there's a non-trivial probability that any input contains it, so this is a genuine property of the data distribution. It feels analogous to the model learning bigrams or trigrams, which are basically memorising 2 or 3 token substrings - in some sense this is memorisation, but to me it's a genuine feature of the data distribution.
My best attempt to operationalise memorisation is that it's about ways that the training data that differs from the training data distribution. If some string has infinitessimal probability of occurring in a randomly sampled data point, but occurs in a single training example, then that feels like memorisation. But if something occurs in a bunch of training examples, it probably occurs with non-trivial probability in any sample from data distribution.
Alternately, it's memorisation if it results in significantly better loss on the training set than test set (assuming they're from the same data distribution).
I might be relying too hard on the notion of a data distribution though.
This also feels like an interesting difference between continuous data like images and discrete data like language - language can often have identical substrings in a way that seems much weirder in images (patches that are identical down to the pixel level?), so it feels harder to disentangle memorisation from generalisation in language.
An operational definition which I find helpful for thinking about memorization is Zhang et al's counterfactual memorization.
The counterfactual memorization of a document is (roughly) the amount that the model's loss on degrades when you remove from its training dataset.
More precisely, it's the difference in expected loss on between models trained on data distribution samples that happen to include , and models trained on data distribution samples that happen not to include .
This will be lower for documents that are easy for the LM to predict using general features learned elsewhere, and higher for documents that the LM can't predict well except by memorizing them. For example (these are intuitive guesses, not experimental results!):
- A document containing a list of random UUIDs will have higher counterfactual memorization than a document containing the word "the" repeated many times.
- If we extend the definition slightly to cover training sets with fewer or more copies of a document , then a document repeated many times in the training set will have higher counterfactual memorization than a document that appears only once.
- Repeating many times, or doing many epochs over it, will produce more counterfactual memorization than doing the same thing with . (The counterfactual memorization for is upper bounded by the loss on attained by a model that never even sees it once in training, and that's already low to begin with.)
Note that the true likelihood under the data distribution only matters through its effect on the likelihood predicted by the LM. On average, likely texts will be easier than unlikely ones, but when these two things come apart, easy-vs-hard is what matters. is more plausible as natural text than , but it's harder for the LM to predict, so it has higher counterfactual memorization.
On the other hand, if we put many near duplicates of a document in the dataset -- say, many copies with a random edit to a single token -- then every individual near-duplicate will have low counterfactual memorization.
This is not very satisfying, since it feels like something is getting memorized here, even if it's not localized in a single document.
To fix the problem, we might imagine broadening the concept of "whether a document is in the training set." For example, instead of keeping or removing an literal document, we might keep/remove every document that includes a specific substring like a Bible quote.
But if we keep doing this, for increasingly abstract and distant notions of "near duplication" (e.g. "remove all documents that are about frogs, even if they don't contain the word 'frog'") -- then we're eventually just talking about generalization!
Perhaps we could define memorization in a more general way in terms of distances along this spectrum. If we can select examples for removal using a very simple function, and removing the selected examples from the training set destroys the model's performance on them, then it was memorizing them. But if the "document selection function" grows more complex, and starts to do generalization internally, we then say the model is generalizing as opposed to memorizing.
(ETA: though we also need some sort of restriction on the total number of documents removed. "Remove all documents containing some common word" and "remove all but the first document" are simple rules with very damaging effects, but obviously they don't tell us anything about whether those subsets were memorized.)
Hmm, this comment ended up more involved than I originally intended ... mostly I wanted to drop a reference to counterfactual memorization. Hope this was of some interest anyway.
Super interesting, thanks! I hadn't come across that work before, and that's a cute and elegant definition.
To me, it's natural to extend this to specific substrings in the document? I believe that models are trained with documents chopped up and concatenated to fit into segment that fully fit the context window, so it feels odd to talk about document as the unit of analysis. And in some sense a 1000 token document is actually 1000 sub-tasks of predicting token k given the prefix up to token k-1, each of which can be memorised.
Maybe we should just not apply a gradient update to the tokens in the repeated substring? But keep the document in and measure loss on the rest.
I'm curious how you'd define memorisation? To me, I'd actually count this as the model learning features ...
Qualitatively, when I discuss "memorization" in language models, I'm primarily referring to the phenomenon of languages models producing long quotes verbatim if primed with a certain start. I mean it as a more neutral term than overfitting.
Mechanistically, the simplest version I imagine is a feature which activates when the preceding N tokens match a particular pattern, and predicts a specific N+1 token. Such a feature is analogous to the "single data point features" in this paper. In practice, I expect you can have the same feature also make predictions about the N+2, N+3, etc tokens via attention heads.
This is quite different from a normal feature in the fact that it's matching a very specific, exact pattern.
a bunch of examples will contain the Bible verse as a substring, and so there's a non-trivial probability that any input contains it, so this is a genuine property of the data distribution.
Agreed! This is why I'm describing it as "memorization" (which, again, I mean more neutrally than overfitting in the context of LLMs) and highlight that it really does seem like language models morally should do this.
Although there's also lots of SEO spam that language models memorize because it's repeated which one might think of as overfitting, even though they're a property of the training distribution.
Interesting stuff!
In this toy model, is it really the case that the datapoint feature solutions are "more memorizing, less generalizing" than the axis-aligned feature solutions? I don't feel totally convinced of this.
Two ways to look at the toy problem:
- There are sparse features, one per input and output channel.
- There are sparse features, one per data point, and each one is active only on its data point. The features are related to the input basis by some matrix .
There are some details of the toy model that put (2) on a "different footing" from (1).
Since the input and output use the same basis, if we make a change of basis, we have to change back again at the end. And because the weights are tied, these two operations have to be transposes, i.e. the change of basis has to be a rotation.
As illustrated in the Colab, requiring the data to be orthonormal is sufficient for this. The experiment constrained the data to unit norm, and it's close to orthogonal with high probability for .
Now, it happens that (1) is the true data-generating process, but the model has no way of guessing that. In the finite-data case, the data may be consistent with multiple data-generating processes, and a solution that generalizes well with respect to one of them may generalize poorly with respect to another.
To designate one data-generating process as the relevant one for generalization, we have to make a value judgment about which hypotheses are better, among those that explain the data equally well.
In particular, when , hypothesis (2) seems more parsimonious than hypothesis (1): it explains the data just as well with fewer features! The features aren't axis-aligned like in (1), but features in real problems won't be axis-aligned either.
In some sense, it does feel like there's a suspicious lack of generalization in (2). Namely, that no generalization is made between the training examples: any knowledge you gain about a feature from seeing one example will go unused on the rest of the training set. But if your data is small enough that is almost entirely orthogonal, hypothesis (1) has the same problem: the feature weight in each training example has almost no overlap with the other examples.
In this toy model, is it really the case that the datapoint feature solutions are "more memorizing, less generalizing" than the axis-aligned feature solutions? I don't feel totally convinced of this.
Well, empirically in this setup, (1) does generalize and get a lower test loss than (2). In fact, it's the only version that does better than random. 🙂
But I think what you're maybe saying is that from the neural network's perspective, (2) is a very reasonable hypothesis when T < N, regardless of what is true in this specific setup. And you could perhaps imagine other data generating processes which would look similar for small data sets, but generalize differently. I think there's something to that, and it depends a lot on your intuitions about what natural data is like.
Some important intuitions for me are:
- Many natural language features are extremely sparse. For example, it seems likely LLMs probably have features for particular people, for particular street intersections, for specific restaurants... Each of these features is very very rarely occurring (many are probably present less than 1 in 10 million tokens).
- Simultaneously, there are an enormous number of features (see above!).
- While the datasets aren't actually small, repeated data points effectively make many data points behave like we're in the small data regime (see Adam's repeated data experiment).
Thus, my intuition is that something directionally like this setup -- having a large number of extremely sparse features -- and then studying how representations change with dataset size is quite relevant. But that's all just based on intuition!
(By the way, I think there is a very deep observations about the duality of (1) vs (2) and T<N. See the observations about duality in https://arxiv.org/pdf/2210.16859.pdf )
Thanks for the great comment clarifying your thinking!
I would be interested in seeing the data dimensionality curve for the validation set on MNIST (as opposed to just the train set) - it seems like the stated theory should make pretty clear predictions about what you'd see. (Or maybe I'll try to make reproduction happpen and do some more experiments).
These results also suggest that if superposition is widespread, mechanistic anomaly detection will require solving superposition
I feel pretty confused, but my overall view is that many of the routes I currently feel are most promising don't require solving superposition. At least, they don't require solving superposition in the sense I think you mean. I'm not sure the rest of my comment here will make sense without more context, but I'll try.
Specifically, these routes require decoding superposition, but not obviously more so than training neural networks requires decoding superposition. Overall, the hope would be something like 'SGD is already finding weights which decode the representations the NN is using, so we can learn a mechanistic "hypothesis" for how these weights work via SGD itself'. I think this exact argument doesn't quite pan out (see here for related discussion) and it's not clear what we need as far as mechanistic 'hypotheses' go.
I feel pretty confused, but my overall view is that many of the routes I currently feel are most promising don't require solving superposition.
It seems quite plausible there might be ways to solve mechanistic interpretability which frame things differently. However, I presently expect that they'll need to do something which is equivalent to solving superposition, even if they don't solve it explicitly. (I don't fully understand your perspective, so it's possible I'm misunderstanding something though!)
To give a concrete example (although this is easier than what I actually envision), let's consider this model from Adam Jermyn's repeated data extension of our paper:

If you want to know whether the model is "generalizing" rather than "triggering a special case" you need to distinguish the "single data point feature" direction from normal linear combinations of features. Now, it happens to be the case that the specific geometry of the 2D case we're visualizing here means that isn't too hard. But we need to solve this in general. (I'm imagining this as a proxy for a model which has one "special case backdoor/evil feature" in superposition with lots of benign features. We need to know if the "backdoor/evil feature" activated rather than an unusual combination of normal features.)
Of course, there may be ways to distinguish this without the language of features and superposition. Maybe those are even better framings! But if you can, it seems to me that you should then be able to backtrack that solution into a sparse coding solution (if you know whether a feature has fired, it's now easy to learn the true sparse code!). So it seems to me that you end up having done something equivalent.
Again, all of these comments are without really understanding your view of how these problems might be solved. It's very possible I'm missing something.
Overall, my view is that we will need to solve the optimization problem of 'what properties of the activation distribution are sufficient to explain how the model behaves', but this solution can be represented somewhat implicitly and I don't currently see how you'd transition it into a solution to superposition in the sense I think you mean.
I'll try to explain why I have this view, but it seems likely I'll fail (at least partially because of my own confusions).
Quickly, some background so we're hopefully on the same page (or at least closer):
I'm imagining the setting described here. Note that anomalies are detected with respect to a distribution (for a new datapoint ! So, we need a distribution where we're happy with the reason why the model works.
This setting is restrictive in various ways (e.g., see here), but I think that practical and robust solutions would be a large advancement regardless (extra points for an approach which fails to have on paper counterexamples).
Now the approaches to anomaly detection I typically think about work roughly like this:
- Try to find an 'explanation'/'hypothesis' for the variance on which doesn't also 'explain' deviation from the mean on . (We're worst casing over explanations)
- If we succeed, then is anomalous. Otherwise, it's considered non-anomalous.
Note that I'm using scare quotes around explanation/hypothesis - I'm refering to an object which matches some of the intutive properties of explanations and/or hypotheses, but it's not clear exactly which properties we will and won't need.
This stated approach is very inefficient (it requires learning an explanation for each new datum !), but various optimizations are plausible (e.g., having a minimal base explanation for which we can quickly finetune for each datum ).
I'm typically thinking about anomaly detection schemes which use approaches similar to causal scrubbing, though Paul, Mark, and other people at ARC typically think about heuristic arguments (which have quite different properties).
Now back to superposition.
A working solution must let you know if atypical features have fired, but not which atypical features or what direction those atypical features use. Beyond this, we might hope that the 'explanation' for the variance on can tell use which directions the model uses for representing important information. This will sometimes be true, but I think this is probably false in general, though I'm having trouble articulating my intuitions for this. Minimally, I think it's very unclear how you would extract this information if you use causal scrubbing based approaches.
I plan on walking through an example which is similar to how we plan on tacking anomaly detection with causal scrubbing in a future comment, but I need to go get lunch.
(This is a follow up to Anthropic's prior work on Toy Models of Superposition.)
The authors study how neural networks interpolate between memorization and generalization in the "ReLU Output" toy model from the first toy model paper:
They train models to perform a synthetic regression task with T training points, for models with m hidden dimensions.
First, they find that for small training sets, while the features are messy, the training set hidden vectors hi=WXi (the projection of the input datapoints into the hidden space) often show clean structures:
They then extend their old definition of feature dimensionality to measure the dimensionalities allocated to each of the training examples:
DXi = ||hi||2∑j(^hi⋅hj)2
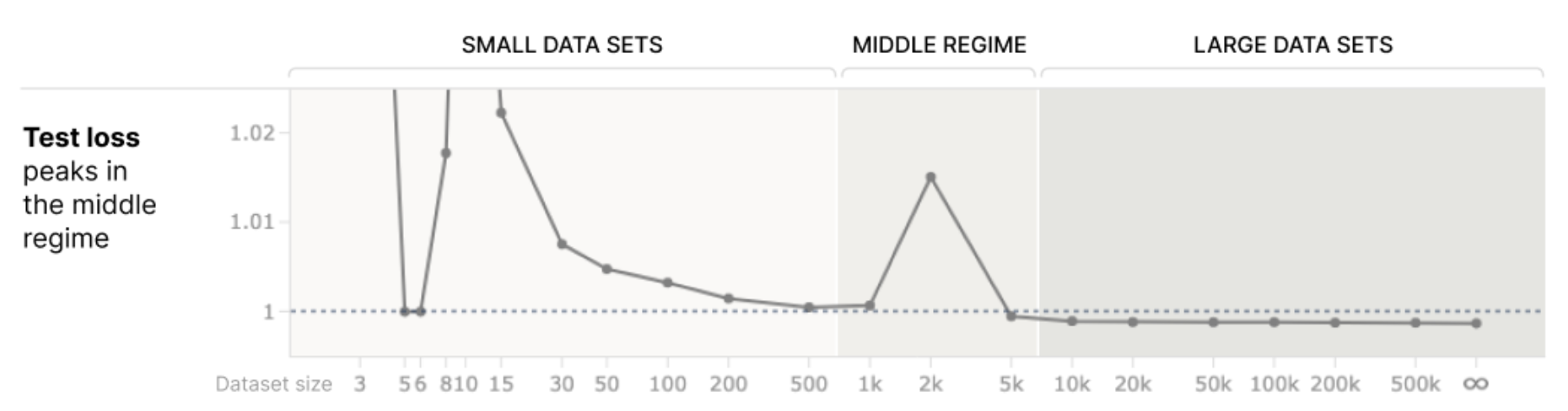
and plot this against the data set size (and also test loss):
This shows that as you increase the amount of data, you go from a regime with high dimensionality allocated to training vectors and low dimensionality allocated to features, to one where the opposite is true. In between the two, both feature and hidden vector dimensionalities receive low dimensionality, which coincides with an increase in test loss, which they compare to the phenomena of "data double descent" (where as you increase data on overparameterized models with small amounts of regularization, test loss can go up before it goes down).
Finally, they visualize how varying T and m affects test loss, and find double descent along both dimensions:
They also included some (imo very interesting) experiments from Adam Jermyn, 1) replicating the results, 2) exploring how weight decay interacts with this double descent-like phenomenon, and 3) studying what happens if you repeat particular datapoints.
Some limitations of the work, based on my first read through:
(I'll probably have more thoughts as I think for longer.)