In his latest post, Logical Pinpointing, Eliezer talks about the nature of math. I have my own views on the subject, but when writing about them, it became too long for a comment, so I'm posting it here in discussion.
I think it's important to clarify that I am not posting this under the guise that I am correct. I'm just posting my current view of things, which may or may not be correct, and which has not been assessed by others yet. So though I have pushed myself to write in a confident (and clear) tone, I am not actually confident in my views ... well, okay, I'm lying. I am confident in my views, but I know I shouldn't be, so I'm trying to pretend to myself that I'm posting this to have my mind changed, when in reality I'm posting it with the stupid expectation that you'll all magically be convinced. Thankfully, despite all that, I don't have a tendency to cling to beliefs which I have seen proven wrong, so I will change my mind when someone kicks my belief's ass. I won't go down without a fight, but once I'm dead, I'm dead.
Before I can share my views, I need to clarify a few concepts, and then I'll go about showing what I believe and why.
Abstractions
Abstract models are models in which some information is ignored. Take, for example, the abstract concept of the ball. I don't care if the ball is made of rubber or steel, nor do I care if it has a radius of 6.7cm or a metre, a ball is a ball. I couldn't care less about the underlying configuration of quarks in the ball, as long as it's a sphere.
Numbers are also abstractions. If I've got some apples, when I abstract this into a number, I don't care that they are apples. All I care about is how many there are. I can conveniently forget about the fact that it's apples, and about the concept of time, and the hole in my bag through which the apples might fall.
Axiomatic Systems (for example, Peano Arithmetic)
Edit: clarified this paragraph a bit.
I don't have much to say about these for now, except that they can all be reduced to physics. Given that mathematicians store axiomatic systems in their minds, and use them to prove things, they cannot help but be reducible to physical things, unless the mind itself is not physical. I think most LessWrongers, being reductionists, believe this, so I won't go into much more detail. I'll just say that this will be important later on.
I Can Prove Things About Numbers Using Apples
Let's say I have 2 apples. Then someone gives me 2 more. I now have 4. I have just shown that 2+2=4, assuming that apples behave like natural numbers (which they do).
But let's continue this hypothetical. As I put my 2 delicious new apples into my bag, one falls out through a hole in my bag. So if I count how many I have, I see 3. I had 2 to begin with, and 2 more were given to me. It seems I have just shown 2+2=3, if I can prove things about numbers using apples.
The problem lies in the information that I abstracted away during the conversion from apples to numbers. Because my conversion from apples to numbers failed to include information about the hole, my abstract model gave incorrect results. Like my predictions about balls might end up being incorrect if I don't take into account every quark that composes it. Upon observing that the apple had fallen through the hole, I would realize that an event which rendered my model erroneous had occurred, so I would abstract this new event into -1, which would fix the error: 2+2-1=3.
To summarize this section, I can "prove" things about numbers using apples, but because apples are not simple numbers (they have many properties which numbers don't), when I fail to take into account certain apple properties which will affect the number of apples I have, I will get incorrect results about the numbers.
Apples vs Peano Arithmetic
We know that Peano Arithmetic describes numbers very well. Numbers emerge in PA; we designed PA to do so. If PA described unicorns instead, it wouldn't be very useful. And if PA emerges from the laws of physics (we can see PA emerge in mathematicians' minds, and even on pieces of paper in the form of writing), then the numbers which emerge from PA emerge from the laws of physics. So there is nothing magical about PA. It's just a system of "rules" (physical processes) from which numbers emerge, like apples (I patched up the hole in my bag ;) ).
Of course, PA is much more convenient for proving things about numbers than apples. But they are inherently just physical processes from which I have decided to ignore most details, to focus only on the numbers. In my bag of 3 apples, if I ignore that it's apples there, I get the number 3. In SSS0, if I forget about the whole physical process giving emergence to PA, I am just left with 3.
So I can go from 3 apples to the number 3 by removing details, and from the number 3 to PA by adding in a couple of details. I can likewise go from PA to numbers, and then to apples.
To Conclude, Predictions are "Proofs"
From all this, I conclude that numbers are simply an abstraction which emerges in many places thanks to our uniform laws of physics, much like the abstract concept "ball". I also conclude that what we classify as a "prediction" is in fact a "proof". It's simply using the rules to find other truths about the object. If I predict the trajectory of a ball, I am using the rules behind balls to get more information about the ball. If I use PA or apples to prove something about numbers, I am using the rules behind PA (or apples) to prove something about the numbers which emerge from PA (or apples). Of course, the proof with PA (or apples) is much more general than the "proof" about the ball's trajectory, because numbers are much more abstract than balls, and so they emerge in more places.
So my response to this part of Eliezer's post:
Never mind the question of why the laws of physics are stable - why is logic stable?
Logic is stable for the same reasons the laws of physics are stable. Logic emerges from the laws of physics, and the laws of physics themselves are stable (or so it seems). In this way, I dissolve the question and mix it with the question why the laws of physics are stable -- a question which I don't know enough to attempt to answer.
Edit: I'm going to retract this and try to write a clearer post. I still have not seen arguments which have fully convinced me I am wrong, though I still have a bit to digest.

Hmm... Another good argument. This one is harder. But that's just making this more fun, and getting me closer to giving in.
If I abstract a whole bunch of details about apples away, except the number and the fact that it's an apple, I get math with units. So if I have a bag of 3 apples, I can abstract this to 3apples. I can add 1apple to this, and get 4apples. Why? Some ancient mathematicians have shown that when you retain this extra bit of information, the abstraction "math with units" is formed, which is pretty much exactly like normal math, except that numbers are multiplied by their units. "math with units" and plain old math are very similar because they are both numbers, but "math with units" happens to retain a few extra details about what the numbers are talking about.
1apple 1apple=1apple^2 is true, but it doesn't make sense. You can't add in details to turn this into apples because of physical limitations, so 1apple 1apple does not emerge from apples. But it is consistent with the rules of mathematics, which you obtain when you remove the complex details of what an apple is, so this is considered true.
1m * 1m=1m^2, however, does make sense, and we can add in details to transform this into an area. m/s can be transformed into the speed of an object by adding in details. m/s^2 can be transformed into an actual acceleration. kgm/s^2 can be transformed into an actual force by adding in details. I think this is true of all useful units, but if you can think of one for which this is not true, please share, because that will be a big blow to my theory. If this theory survives all the other arguments, I will still need to prove that this is true, and until I prove it, my theory is weak. Thank you for showing me this.
Anyway, a summary of this comment: math with units is an abstraction, one level below plain math, and it mostly follows the rules of math because it's just math+(some simple other thing). Units which don't make sense cannot be un-abstracted into things in the world, but because math is consistent, we can still manipulate them like anything else because we have abstracted the details which makes it not make sense away.
So I needed to extend my theory for this, but thankfully not by making it more complex at the base. This is all just emergent stuff in the universe. So if my theory holds up, I expect Occam's Razor will be in favor of it.
Quantities can be converted to and from numbers:
(32 ft lbf / (lbm sec^2))=1
(64 ft lbf / (lbm sec^2))=2
It is true, but not useful, to say that the area of a circle with radius R is equal to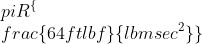
or equivalently,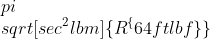
Taking the sec^2lbf root does not have an analogue in reality, but the units output from taking the time^2*Force root of a distance raised to the power of scalar*distance*mass is area in this specific case.