The Useful Idea of Truth
56Kaj_Sotala
21[anonymous]
42Eliezer Yudkowsky
49pragmatist
14Eliezer Yudkowsky
4PaulWright
0torekp
5common_law
0torekp
19pragmatist
19lukeprog
20MichaelVassar
1DaFranker
0lukeprog
15Paul Crowley
3DuncanS
0betterthanwell
3lukeprog
0betterthanwell
0betterthanwell
0betterthanwell
8pragmatist
4[anonymous]
2Eliezer Yudkowsky
4Richard_Kennaway
0lukeprog
0thomblake
0Vaniver
9lukeprog
2gwern
3lukeprog
0[anonymous]
38yli
8Eliezer Yudkowsky
3TimS
7Eliezer Yudkowsky
17Kaj_Sotala
11TimS
5Viliam_Bur
2TheOtherDave
1Eliezer Yudkowsky
48novalis
24[anonymous]
23Kaj_Sotala
7thomblake
4Eliezer Yudkowsky
23[anonymous]
9Eliezer Yudkowsky
11[anonymous]
10Jonathan_Elmer
7Scottbert
4lukeprog
5fubarobfusco
5BerryPick6
2lukeprog
-1MugaSofer
1BerryPick6
1MugaSofer
1TheWakalix
4thomblake
-1[anonymous]
1thomblake
1DaFranker
5yli
3Scottbert
31Alex_Altair
0danceapocalypse
31Wei Dai
11Viliam_Bur
2Bluehawk
-3Chrysophylax
11amcknight
3pragmatist
0Peterdjones
1V_V
3TheOtherDave
-1V_V
0Wei Dai
2V_V
-2Wei Dai
2V_V
1Wei Dai
1faul_sname
1Benquo
5DuncanS
0Peterdjones
0A1987dM
24fubarobfusco
13jbash
6TimS
-2DSimon
10Kaj_Sotala
7TimS
0MixedNuts
5TimS
2MixedNuts
23TimS
0Douglas_Knight
5MichaelVassar
1[anonymous]
3TimS
0[anonymous]
1DaFranker
-2Eugine_Nier
7TimS
7[anonymous]
21thomblake
24MBlume
0thomblake
21daenerys
25Eliezer Yudkowsky
7arundelo
3Alex_Altair
3A1987dM
7Eliezer Yudkowsky
7lukeprog
17Eliezer Yudkowsky
64daenerys
19Richard_Kennaway
-3Eliezer Yudkowsky
53Scott Alexander
38daenerys
12Scott Alexander
4johnlawrenceaspden
-3RationalAsh
5FluffyC
1Dentin
1FluffyC
1Rixie
0Desrtopa
1Rixie
0RationalAsh
-4Rixie
6Peterdjones
2JulianMorrison
11[anonymous]
24Kaj_Sotala
22JulianMorrison
14Richard_Kennaway
2TheOtherDave
1Richard_Kennaway
7TheOtherDave
6A1987dM
14[anonymous]
9garethrees
16loup-vaillant
9Alejandro1
4loup-vaillant
2Rixie
5evand
2loup-vaillant
9[anonymous]
8Manfred
9Vaniver
5Ender
1buybuydandavis
15Richard_Kennaway
4dankane
5Richard_Kennaway
2dankane
0Richard_Kennaway
0dankane
0Richard_Kennaway
0dankane
0A1987dM
2Bundle_Gerbe
14RobinZ
0[anonymous]
0RobinZ
0[anonymous]
5RobinZ
14Scott Alexander
22MixedNuts
6Salutator
2Scott Alexander
0Salutator
1pragmatist
0siodine
0Nisan
7Scott Alexander
0Nisan
0Scott Alexander
3Nisan
0Shmi
0Scott Alexander
2MBlume
-4Kawoomba
12JulianMorrison
0Yosarian2
0Matt_Simpson
1JulianMorrison
0Matt_Simpson
0JulianMorrison
0Eugine_Nier
8Bundle_Gerbe
2thomblake
5ArisKatsaris
11Eugine_Nier
7khafra
6dankane
4CCC
2dankane
2RobinZ
0dankane
2RobinZ
2dankane
3RobinZ
2dankane
2RobinZ
0Bobertron
-1ArisKatsaris
4[anonymous]
4Vaniver
2RobinZ
3katydee
1Pavitra
0almkglor
-2Pavitra
-2MugaSofer
2[anonymous]
2Karl
2mbrubeck
0DuncanS
2selylindi
0MixedNuts
0selylindi
2MixedNuts
2selylindi
2somervta
2Patrick
2Furslid
2RobinZ
2Dolores1984
1One
1jvmack
1EniScien
1seanwelsh77
1alex_zag_al
1Benquo
1Alex_Altair
0Cakoluchiam
0[anonymous]
0CCC
0DSimon
0Eugine_Nier
0DSimon
0Eugine_Nier
0wedrifid
0TheOtherDave
0DuncanS
0[anonymous]
0dankane
1heresieding
0Nisan
12Furslid
1Nisan
5Scott Alexander
1thomblake
0wedrifid
2Nisan
0wedrifid
2thomblake
2[anonymous]
0thomblake
0Pavitra
0Nisan
0[anonymous]
4dankane
-8siodine
-9[anonymous]
3ArisKatsaris
0[anonymous]
2pragmatist
-2[anonymous]
0Peterdjones
-2[anonymous]
0Peterdjones
16selylindi
2Eliezer Yudkowsky
29Shmi
2Eliezer Yudkowsky
14buybuydandavis
12CarlShulman
10Eliezer Yudkowsky
2wedrifid
1TimS
1Eliezer Yudkowsky
10wedrifid
1Eliezer Yudkowsky
8Eugine_Nier
4wedrifid
2Normal_Anomaly
0Daniel_Burfoot
0wedrifid
1TheAncientGeek
0onelasttime
11earthwormchuck163
10common_law
10Sniffnoy
3DuncanS
9kilobug
24TimS
4fubarobfusco
1TimS
0A1987dM
2pleeppleep
8[anonymous]
7ArisKatsaris
4thomblake
2Maelin
2A1987dM
0Normal_Anomaly
6TraderJoe
2learnmethis
0Normal_Anomaly
6CronoDAS
5Benquo
0pleeppleep
2incariol
-2pleeppleep
0CronoDAS
0pleeppleep
-1Larks
5living_philosophy
6TimS
0almkglor
-2living_philosophy
5beoShaffer
4AlexMennen
17Manfred
11Eliezer Yudkowsky
4EricHerboso
4Benquo
7incariol
3learnmethis
2biomachine
4Said Achmiz
1biomachine
2Said Achmiz
1biomachine
5Said Achmiz
1biomachine
2topynate
2purge
2A1987dM
2chaosmosis
2A1987dM
0Normal_Anomaly
0A1987dM
0Normal_Anomaly
0A1987dM
0MixedNuts
0A1987dM
2[anonymous]
10MixedNuts
2[anonymous]
0Peterdjones
0MixedNuts
0Peterdjones
0wedrifid
3Shmi
0Eugine_Nier
2Shmi
-2Peterdjones
4Shmi
0Peterdjones
0Shmi
0Peterdjones
0faul_sname
2incariol
6thomblake
7Eliezer Yudkowsky
-2Bo102010
2Larks
6Eliezer Yudkowsky
4endoself
2fubarobfusco
2pleeppleep
0[anonymous]
1Luiza
1Luiza
1Mis-Understandings
1DragonGod
1DragonGod
1awenonian
1Daemon
1biomachine
1TAG
1biomachine
1TAG
1biomachine
1TAG
1biomachine
-1Daemon
2[anonymous]
1TAG
-2duckduckMOO
1BobTheBob
6Eliezer Yudkowsky
1BobTheBob
15Eliezer Yudkowsky
-2BobTheBob
4Emile
0[anonymous]
0chaosmosis
5BobTheBob
5Richard_Kennaway
2thomblake
4Peterdjones
1hairyfigment
2BobTheBob
2Emile
1thomblake
0Peterdjones
1folkTheory
6fortyeridania
2thomblake
0folkTheory
1Jonathan_Graehl
1[anonymous]
1[anonymous]
1beriukay
0purge
1DuncanS
1anotherblackhat
11thomblake
9Armok_GoB
8wedrifid
0thomblake
2wedrifid
0DaFranker
0wedrifid
2DaFranker
0philh
4earthwormchuck163
6faul_sname
9thomblake
0DaFranker
1Shmi
0Peterdjones
0Shmi
0Peterdjones
-2Decius
-5Shmi
5pragmatist
1Shmi
2[anonymous]
0Shmi
2Peterdjones
5DaFranker
1thomblake
0DaFranker
1nshepperd
0Shmi
1nshepperd
-3Shmi
-2Decius
0Shmi
2DaFranker
2Shmi
2thomblake
-2Decius
0Peterdjones
0Decius
-2Peterdjones
0Arthur Milchior
8Elo
0Gram_Stone
0[anonymous]
0TruePath
1DaFranker
0TruePath
0ChristianKl
0DaFranker
3TheAncientGeek
0IainM
0IainM
0[anonymous]
0Jonathan_Elmer
4amcknight
1Jonathan_Elmer
1amcknight
0Jonathan_Elmer
0amcknight
0DaFranker
-1Jonathan_Elmer
0Matt_Simpson
2wedrifid
4Matt_Simpson
2wedrifid
2Matt_Simpson
0shokwave
0Peterdjones
0Larks
0Jonathan_Elmer
0Pavitra
0JackV
2[anonymous]
1evand
0[anonymous]
1evand
-1Shmi
8ArisKatsaris
4V_V
2khafra
-2Shmi
-1ArisKatsaris
0Shmi
0pragmatist
0Shmi
2pragmatist
4TheOtherDave
0Shmi
0TheOtherDave
-1Shmi
-2darrenreynolds
3TheOtherDave
0darrenreynolds
0nshepperd
0TheOtherDave
0darrenreynolds
1TheOtherDave
0BerryPick6
5wedrifid
0BerryPick6
2Alejandro1
1ArisKatsaris
0darrenreynolds
6A1987dM
5ArisKatsaris
0[anonymous]
-1Shmi
0wedrifid
-3David
-6Shmi
15Eliezer Yudkowsky
-8Shmi
2Eliezer Yudkowsky
1Shmi
-1[anonymous]
2Shmi
0[anonymous]
5Kawoomba
-10Shmi
19jimrandomh
8A1987dM
-3Clippy
4ArisKatsaris
New Comment
Rendering 547/548 comments, sorted by (show more) Click to highlight new comments since:
I just realized that since I posted two comments that were critical over a minor detail, I should balance it out by mentioning that I liked the post - it was indeed pretty elementary, but it was also clear, and I agree about it being considerably better than The Simple Truth. And I liked the koans - they should be a useful device to the readers who actually bother to answer them.
Also:
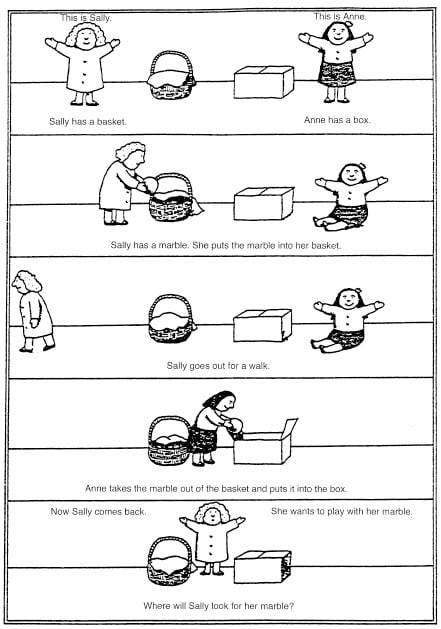
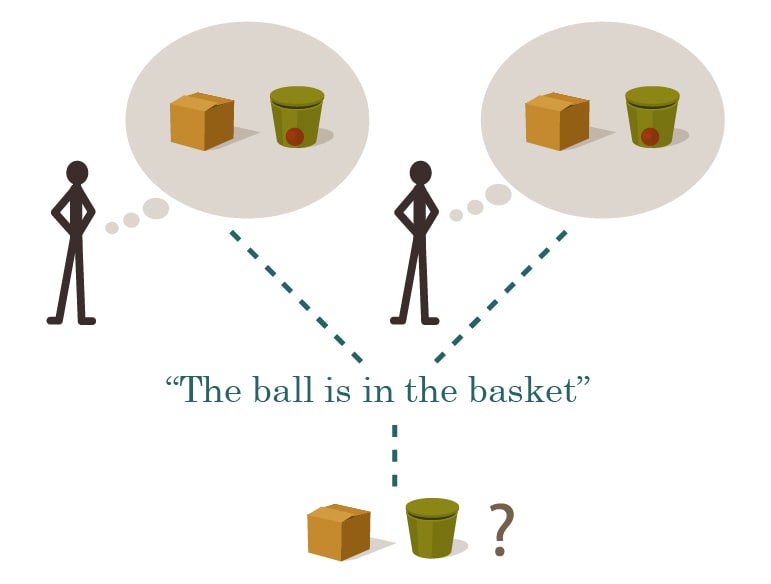
Human children over the age of (typically) four, first begin to understand what it means for Sally to lose her marbles - for Sally's beliefs to stop corresponding to reality.
was a cute touch.
Thank you for being positive.
I've been recently thinking about this, and noticed that despite things like "why our kind can't cooperate", we still focus on criticisms of minor points, even when there are major wins to be celebrated.
(The 'Mainstream Status' comment is intended to provide a quick overview of what the status of the post's ideas are within contemporary academia, at least so far as the poster knows. Anyone claiming a particular paper precedents the post should try to describe the exact relevant idea as presented in the paper, ideally with a quote or excerpt, especially if the paper is locked behind a paywall. Do not represent large complicated ideas as standard if only a part is accepted; do not represent a complicated idea as precedented if only a part is described. With those caveats, all relevant papers and citations are much solicited! Hopefully comment-collections like these can serve as a standard link between LW presentations and academic ones.)
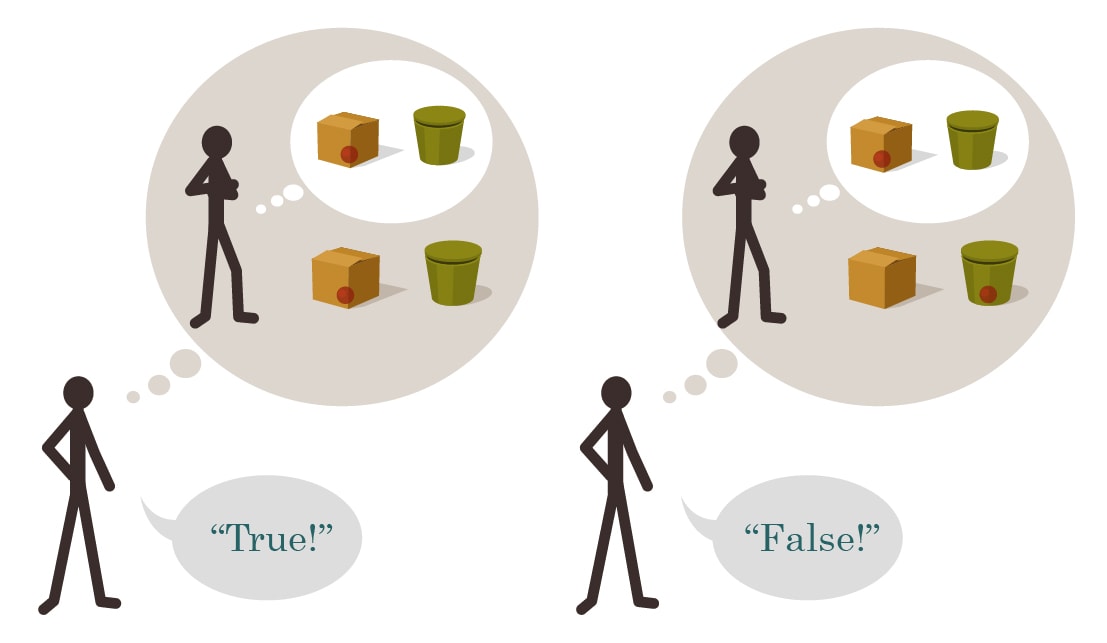
The correspondence theory of truth is the first position listed in the Stanford Encyclopedia of Philosophy, which is my usual criterion for saying that something is a solved problem in philosophy. Clear-cut simple visual illustration inspired by the Sally-Anne experimental paradigm is not something I have previously seen associated with it, so the explanation in this post is - I hope - an improvement over what's standard.
Alfred Tarski is a famous mat...
This is a great post. I think the presentation of the ideas is clearer and more engaging than the sequences, and the cartoons are really nice. Wild applause for the artist.
I have a few things to say about the status of these ideas in mainstream philosophy, since I'm somewhat familiar with the mainstream literature (although admittedly it's not the area of my expertise). I'll split up my individual points into separate comments.
Alfred Tarski is a famous mathematician whose theory of truth is widely known.
Summary of my point: Tarski's biconditionals are not supposed to be a definition of truth. They are supposed to be a test of the adequacy of a proposed definition of truth. Proponents of many different theories claim that their theory passes this test of adequacy, so to identify Tarski's criterion with the correspondence theory is incorrect, or at the very least, a highly controversial claim that requires defense. What follows is a detailed account of why the biconditionals can't be an adequate definition of truth, and of what Tarski's actual theory of truth is.
Describing Tarski's biconditionals as a definition of truth or a theory of truth is misleading. The relevant paper is ...
I've slightly edited the OP to say that Tarski "described" rather than "defined" truth - I wish I could include more to reflect this valid point (indeed Tarski's theorems on truth are a lot more complicated and so are surrounding issues, no language can contain its own truth-predicate, etc.), but I think it might be a distraction from the main text. Thank you for this comment though!
4
The latest Rationally Speaking post looks relevant: Ian Pollock describes aspects of Eliezer's view as "minimalism" with a link to that same SEP article. He also mentions Simon Blackburn's book, where Blackburn describes minimalists or quietists as making the same point Eliezer makes about collapsing "X is true" to "X" and a similar point about the usefulness of the term "truth" as a generalisation (though it seems that minimalists would say that this is only a linguistic convenience, whereas Eliezer seems to have a slightly difference concept of it in that he wants to talk in general about how we get accurate beliefs).
0
Thanks for this whole comment. In particular,
My gut instinct is deflationist, but I don't see this view as being opposed to "correspondence". The alleged conflict is dubious at best. Stanford Encyclopedia of Philosophy writes:
Emphasis added: the italicized premise is false. Explanation is a cognitive feat, and the same fact (even if the identity is a necessary one) can be cognized in different ways. (Such explanations occur frequently enough in mathematics, I think.) The SEP author anticipates my objection and writes:
It is open to them to argue that "because" does not create a hyper-intensional context, but it is much more plausible that it does. So until a good argument comes along, mark me down as a correspondence deflationist.
5
It's vogue to defend correspondence because 1) it sounds like common sense and 2) it signals rejection of largely discredited instrumentalism. But surely a correspondence theorist should have a theory of the nature of the correspondence. How does a proposition or a verbal string correspond to a state of reality? By virtue of what is it a correct description? We can state a metalinguistic relationship about "Snow is white," but how does this locution hook onto the actual world?
Correspondence theorists think this is a task for a philosophical theory of reference. (Such as in an account where "torekp" refers to you by virtue of the "christening event" of your creating the account and causal connections therefrom.) Deflationists are apt to say it is ultimately a technical problem in the psychology of language.
0
Interesting. I am inclined to replicate my compatibility claim at this level too; i.e., the technical solution in the psychology of language will be a philosophical theory of reference (as much as one needs) as well. I'd be interested in references to any of the deflationist discussions of reference you have in mind.
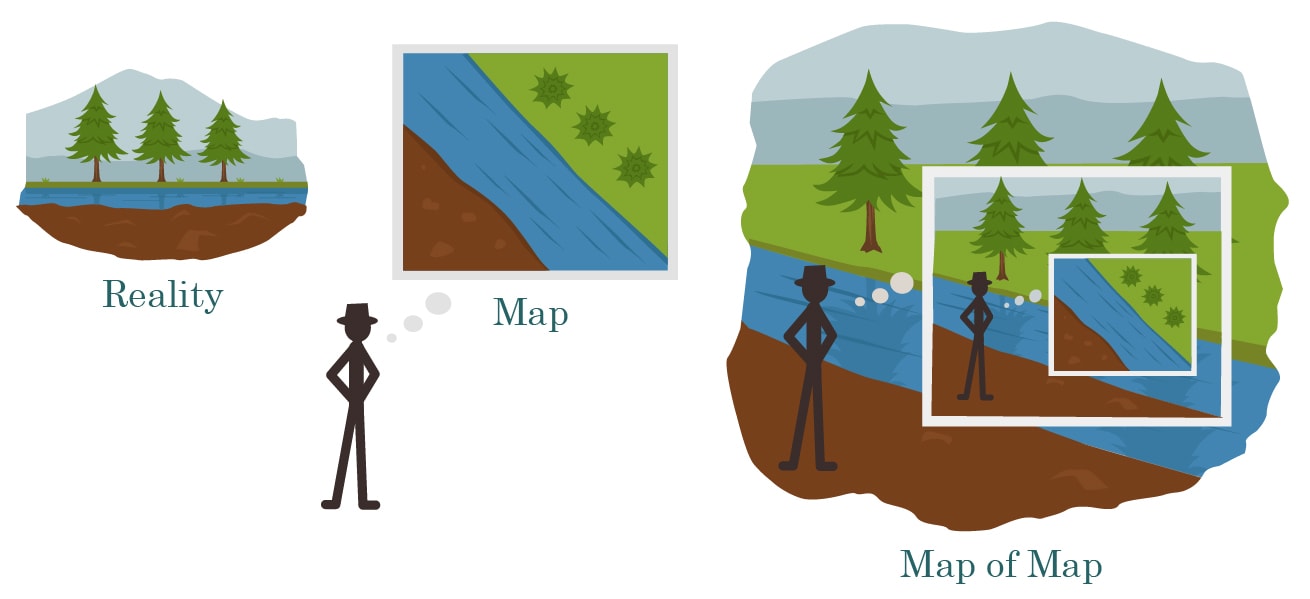
I haven't particularly run across any philosophy explicitly making the connection from the correspondence theory of truth to "There are causal processes producing map-territory correspondences" to "You have to look at things in order to draw accurate maps of them, and this is a general rule with no exception for special interest groups who want more forgiving treatment for their assertions". I would not be surprised to find out it existed, especially on the second clause.
Depends on what you mean by "explicitly". Many correspondence theorists believe that an adequate understanding of "correspondence" requires an understanding of reference -- how parts of our language are associated with parts of the world. I think this sort of idea stems from trying to fill out Tarski's (actual) definition of truth, which I discussed in another comment. The hope is that a good theory of reference will fill out Tarski's obscure notion of satisfaction, and thereby give some substance to his definition of truth in terms of satisfaction.
Anyway, there was a period when a lot of philosophers believed, following Saul Kripke and Hilary Putnam, that we can understan...
Speaking as the author of Eliezer's Sequences and Mainstream Academia...
Off the top of my head, I also can't think of a philosopher who has made an explicit connection from the correspondence theory of truth to "there are causal processes producing map-territory correspondences" to "you have to look at things to draw accurate maps of them..."
But if this connection has been made explicitly, I would expect it to be made by someone who accepts both the correspondence theory and "naturalized epistemology", often summed up in a quote from Quine:
The stimulation of his sensory receptors is all the evidence anybody has had to go on, ultimately, in arriving at his picture of the world. Why not just see how this construction really proceeds? Why not settle for psychology? ...Epistemology, or something like it, simply falls into place as a chapter of psychology and hence of natural science.
(Originally, Quine's naturalized epistemology accounted only for this descriptive part of epistemology, and neglected the normative part, e.g. truth conditions. In the 80s Quine started saying that the normative part entered into naturalized epistemology through "the t...
It's not that clear to me in what sense mainstream academia is a unified thing which holds positions, even regarding questions such as "what fields are legitimate". Saying that something is known in mainstream academia seems suspiciously like saying that "something is encoded in the matter in my shoelace, given the right decryption schema. OTOH, it's highly meaningful to say that something is discoverable by someone with competent 'google-fu"
1
Strongly seconded.
Hell, some "Mainstream" scientists are working on big-money research project that attempt to prove that there's a worldwide conspiracy attempting to convince people that global warming exists so as to make money off of it. Either they're all sell-outs, something which seems very unlikely, or at least some of them actually disagree with some other mainstream scientists, who see the "Is there real global warming?" question as obviously resolved long ago.
0
Agree with all this.
Off the top of my head, I also can't think of a philosopher who has made an explicit connection from the correspondence theory of truth to "there are causal processes producing map-territory correspondences" to "you have to look at things to draw accurate maps of them..."
OK, I defended the tweet that got this response from Eliezer as the sort of rhetorical flourish that gets people to actually click on the link. However, it looks like I also underestimated how original the sequences are - I had really expected this sort of thing to mirror work in mainstream philosophy.
3
Although I wouldn't think of this particular thing as being an invention on his part - I'm not sure I've read that particular chain of thought before, but all the elements of the chain are things I've known for years.
However I think it illustrates the strength of Eliezer's writing well. It's a perfectly legitimate sequence of thought steps that leads in a clear and obvious way to the right answer. It's not new thought, but a particularly clear way of expressing something that many people have thought and written about in a less organised way.
To clarify - there are times when Eliezer is inventive - for example his work on CEV - but this isn't one of those places. I know I'm partly arguing about the meaning of "inventive", but I don't think we're doing him a favor here by claiming this is an example of his inventiveness when there are much better candidates.
0
Karl Popper did so explicitly, thoroughly and convincingly in The Logic of Scientific Discovery. Pretty influential, and definitely a part of "Mainstream Academia."
Here's an interesting, if lengthy, footnote to Chapter 84 - Remarks Concerning the use of the concepts 'True' and 'Corroborated'.
A (short) footnote of my own: Popper's writings have assumed the status of mere "background knowledge", which is a truly great achievement for any philosopher of science. However, The Logic of Scientific discovery is a glorious book which deserves to be even more widely read. Part I of the book spans no more than 30 pages. It's nothing short of beautiful. PDF here.
3
Could you please quote the part of Popper's book that makes the explicit connection from the correspondence theory of truth to "there are causal processes producing map-territory correspondences" to "you have to look at things to draw accurate maps of them..."?
0
Right, this is the obvious next question. I started looking for the appropriate "sound bites" yesterday, but encountered a bit of difficulty in doing so, as I shall explain. Popper's embrace of (Tarskian) correspondence theory should be at least somewhat clear from the footnote I quoted above.
It seems clear to me, from my recount of the book that "you have to look at things to draw accurate maps of them" is one of the chief aims, and one of the central claims of the book; a claim which is defended, by a lengthy, but quite convincing and unusually successful argument - the premises to which are presented only one at a time, and quite meticulously over at least several chapters, so I'm not exactly sure how to go about quoting only the "relevant parts".
My claim that his argument was convincing and successful, is based on the historical observation that popperian falsificationism (the hypothetico-deductive framework) won out over the then quite prevalent logical positivist / verificationist view, to such an extent that it quickly became the default mode of Science, a position it has held, mostly uncontested, ever since, and therefore is barely worthy of mention today. Except when it is, that is; when one encounters problems that are metaphysical (according to Popper), such as Susskind's String Landscape of perhaps 10^500 vacuua, the small (but significant) observed value of the cosmological constant, the (seemingly fine tuned) value of the fine structure constant, and other observations that may require anthropic i.e. metaphysical explanations, since these problems are seemingly not decidable inside of standard, i.e. popperian science.
I feel faced with a claim similar to "I don't believe any mathematician has convincingly proven Fermat's last theorem." To which I reply: Andrew Wiles (1995) The obvious next question is: "Can you please quote the part where he proves the theorem?" This is unfortunately somewhat involved, as the entire 109 page paper tries and succed
0
A (very) quick attempt, perhaps this will suffice? (Let me know if not. )
I begin with the tersest possible defense of my claim that Popper argued that "you actually have to look at things to draw accurate maps of them...", even though this particular example is particularily trivial:
Page 19:
To paraphrase: You have to look actually out the window to discover whether it is raining or not.
----------------------------------------
Continuing, page 16:
(Oops, comment too long.)
0
(Continued)
Page 20:
[a number of indicative, but not decisive quotes omitted]
----------------------------------------
I had hoped to find some decisive sound bite in part one, which is a brief discussion of the epistemological problems facing any theory of scientific method, and an outline of Popper's framework, but it looks like I shall have to go deeper. Will look into this over the weekend.
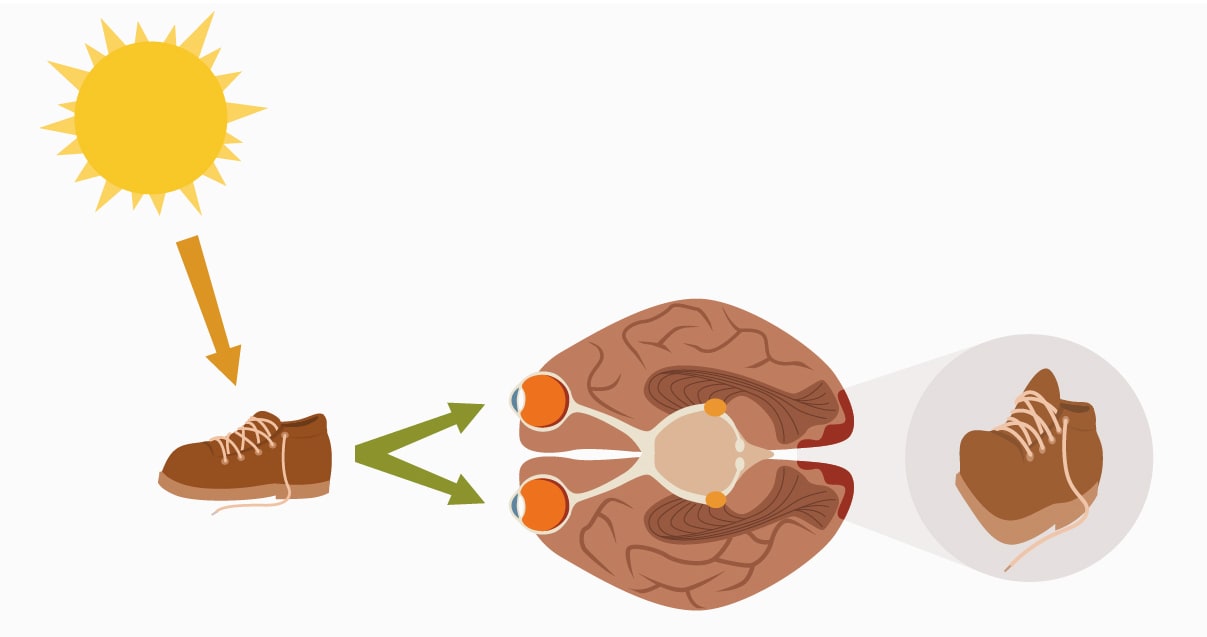
I also found another, though much more recent candidate, David Deutsch in The Beginning of Infinity, Chapter 1 on "The Reach of Explanations". Tough I'm beginning to suspect that although they both point out that "you have to look at things to draw accurate maps of them...", and describe "causal processes producing map-territory correspondences" (for example, between some state of affairs and the output of some scientific instument) both Deutsch and Popper seem to have omitted what one may call the "neuroscience of epistemology." (Where the photon reflects off your shoelace, gets absorbed by your retina, leading to information about the configuration of the world becoming entangled with some corresponding state of your brain, and so on.) This is admittedly quite a crucial step, which Yudkowsky's explanation does cover, and which I cannot recall to have seen elsewhere.
8
Here's a quote from Perry Anderson's recent (highly critical) essay on Gandhi:
4[anonymous]
Trying to include mainstream academia other than philosophy, and going off your blog post "The Second Law of Thermodynamics, and Engines of Cognition", it seems the idea of the general rule that you have to look at and interact with things to form accurate beliefs about them was largely due to Leo Szilard in his 1939 paper "On the Decrease in Entropy in a Thermodynamic System by the Intervention of Intelligent Beings" which analyzed Maxwell's demon thought experiment and introduced the Szilard engine and the entropy cost of gaining information. You gave a more Bayesian analysis than Szilard in that post, possibly going off Jaynes' work in statistical mechanics, like his 1957 papers "Information Theory and Statistical Mechanics" parts one and two, which are the earliest mention of Liouville's theorem I can find in that context. Does Pearl have anything to throw in the mix, like a fancy rule about concluding a past causal interaction when you see corresponding maps and cities?
2
DevilWorm and pragmatist point to the "reliabilism" school of philosophy (http://en.wikipedia.org/wiki/Reliabilism & http://plato.stanford.edu/entries/reliabilism). Clicking on either link reveals arguments concerned mainly with that old dispute over whether the word "knowledge" should be used to refer to "justified true belief". Going on the wording I'm not even sure whether they're considering how photons from the Sun are involved in correlating your visual cortex to your shoelaces. But it does increase the probability of a precedent - does anyone have something more specific? (A lot of the terminology I've seen so far is tremendously vague, and open to many interpretations...)
Incidentally, there might be an even higher probability of finding some explicit precedent in a good modern AI book somewhere?
4
It might be too obvious to be worth mentioning. If you're actually building (narrow) AI devices like self-driving cars, then of course your car has to have a way of sensing things round about it if it's going to build a map of its surroundings.
This fact should be turned into an SMBC cartoon.
0
That's what I was thinking. Maybe in something like Knowledge Representation and Reasoning.
0
AI books tend to assume that one pretty explicitly. For those of a more philosophical bent, some might say something like "The world pushes back", but it's not like anyone doing engineering is in the business of questioning whether the external world exists.
0
Epistemology and the Psychology of Human Judgment (badger's summary) seems relevant, as one of the things they do is attack reliabilism's uselessness. I don't recall any direct precedents, but it's been a while since I read it.
9
Bishop & Trout call their approach "strategic reliabilism." A short summary is here. It's far more Yudkowskian than normal reliabilism. LWers may also enjoy their paper The Pathologies of Standard Analytic Epistemology.
2
That was a pretty cool paper. I don't think I've ever seen SPRs in a philosophy paper before.
3
For the curious, I interviewed Michael Bishop a couple years ago.
0[anonymous]
Process reliabilism maybe? Defines the "justified" part in "justified true belief" as the belief being formed by a reliable truth-producing process.
From the Stanford Encyclopedia of Philosophy article:
Whatever a "causal theory of knowing" is. But it sounds like the kind of thing you're talking about.
I don't like the "post-utopian" example. I can totally expect differing sensory experiences depending on whether a writer is post-utopian or not. For example, if they're post-utopian, when reading their biography I would more strongly expect reading about them having been into utopian ideas when they were young, but having then changed their mind. And when reading their works, I would more strongly expect seeing themes of the imperfectability of the world and weltschmerz.
8
I've edited the OP to try and compartmentalize off the example a bit more.
3
Do you also think the label "Impressionist painter" is meaningless?
7
I have no idea what Impressionism is (I am not necessarily proud of this ignorance, since for all I know it does mean something important). Do you think that a panel of artists would be able to tell who was and wasn't "Impressionist" and mostly agree with each other? That does seem like a good criterion for whether there's sensory data that they're reacting to.
Apparently even computers agree with those judgments (or at least cluster "impressionists" in their own group - I didn't read the paper, but I expect that the cluster labels were added manually).
ETA: Got the paper. Excerpts:
...The dataset includes 994 paintings representing 34 painters, such that each painter has at least 19 images in the dataset. The painters represent several different schools of art such as Early, High, and Northern Renaissance, Mannerism, Baroque, Rococo, Romanticism, Impressionism, Post and Neo Impressionism, Abstract Expressionism, Surrealism, and Fauvism, as commonly defined by art historians. The images were downloaded from various online sources, and normalized to a size of 640,000 pixels while preserving the original aspect ratio. The paintings that were selected for the experiment are assumed to be all in their original condition.
[...] To make the analysis more meaningful for comparing similarities between artistic styles of painters, we selected for each painter paintings that reflect the signature artistic style of that painter. For instance, in Wassily Kandinsky collection we included only paintings representing his abstract expressionism sig
I'm no art geek, but Impressionism is an art "movement" from the late 1800s. A variety of artists (Monet, Renoir, etc) began using similar visual styles that influenced what they decided to paint and how they depicted images.
Art critics think that artistic "movements" are a meaningful way of analyzing paintings, approximately at the level of usefulness that a biologist might apply to "species" or "genus." Or historian of philosophy might talk about the school of thought know today as "Logical Positivism."
Do you think movements is a reasonable unit of analysis (in art, in literature, in philosophy)? If no, why not? If yes, why are you so hostile to the usage of labels like "post-utopian" or "post-colonialist"?
5
The pictures made within an artistic movement have something similar. We should classify them by that something, not only by the movement. Although the name of the movement can be used as a convenient label for the given cluster of picture-space.
If I give you a picture made by unknown author, you can't classify it by author's participation in given movements. But you can classify it by the contents of the picture itself. So even if we use the movement as a label for the cluster, it is better if we can also describe typical properties of picture within that cluster.
Just like when you find a random dog on a street, you can classify it as "dog" species, without taking a time machine and finding out whether the ancestors of this specific dogs really were domesticated wolves. You can teach "dogs are domesticated wolves" at school, but this is not how you recognize dogs in real life.
So how exactly would you recognize "impressionist" paintings, or "post-utopian" books in real life, when the author is unknown? Without teaching this, you are not truly teaching impressionism or post-utopianism.
(In case of "impressionism", my rule of thumb is that the picture looks nice and realistic from distance, but when you stand close to it, the details become somehow ugly. My interpretation of "impressionism" is: work of authors who obviously realized that milimeter precision for a wall painting is an overkill, and you can make pictures faster and cheaper if you just optimize it for looking correct from a typical viewing distance.)
2
I agree with you that there are immediately obvious properties that I use to classify an object into a category, without reference to various other historical and systemic facts about the object. For example, as you say, I might classify a work of art as impressionist based on the precision with which it is rendered, or classify an animal as a dog based on various aspects of its appearance and behavior, or classify food as nutritious based on color, smell, and so forth.
It doesn't follow that it's somehow better to do so than to classify the object based on the less obvious historical or systemic facts.
If I categorize an object as nutritious based on those superficial properties, and later perform a lab analysis and discover that the object will kill me if I eat it, I will likely consider my initial categorization a mistake.
If I share your rule of thumb about "impressionism", and then later realize that some works of art that share the property of being best viewed from a distance are consistently classed by art students as "pointilist" rather than "impressionist", and I further realize that when I look at a bunch of classed-as-pointilist and classed-as-impressionist paintings it's clear to me that paintings in each class share a family resemblance that they don't share with paintings in the other class, I will likely consider my initial rule of thumb a mistake.
Sometimes, the categorization I perform based on properties that aren't immediately apparent is more reliable than the one I perform "in real life."
1
Is this actually a standard term? I was trying to make up a new one, without having to actually delve into the pits of darkness and find a real postmodern literary term that doesn't mean anything.
Maybe you should reconsider picking on an entire field you know nothing about?
I'm not saying this to defend postmodernism, which I know almost nothing about, but to point out that the Sokal hoax is not really enough reason to reject an entire field (any more than the Bogdanov affair is for physics).
I'm pointing out that you're neglecting the virtues of curiosity and humility, at least.
And this is leaving aside that there is no particular reason for "post-utopian" to be a postmodern as opposed to modern term; categorizing writers into movements has been a standard tool of literary analysis for ages (unsurprisingly, since people love putting things into categories).
At this point, getting in cheap jabs at post-modernism and philosophy wherever possible is a well-honored LessWrong tradition. Can't let the Greens win!
I don't think you can avoid the criticism of "literary terms actually do tend to make one expect differing sensory experiences, and your characterization of the field is unfair" simply by inventing a term which isn't actually in use. I don't know whether "post-utopian" is actually a standard term, but yli's comment doesn't depend on it being one.
7
Well, there are a lot of hits for "post-utopian" on Google, and they don't seem to be references to you.
4
I think there were fewer Google references back when I first made up the word... I will happily accept nominations for either an equally portentous-sounding but unused term, or a portentous-sounding real literary term that is known not to mean anything.
Has anyone ever told you your writing style is Alucentian to the core? Especially in the way your municardist influences constrain the transactional nuances of your structural ephamthism.
[This comment is no longer endorsed by its author]
9
This looks promising. Is it real, or did you verify that the words don't mean anything standard?
Alucentian, municardist, and structural ephamthism don't mean anything, though Municard is trademarked. Between Louise Rosenblatt's Transactional Theory in literary criticism and Transactional analysis in psychotherapy, there's probably someone who could define "transactional nuances" for you, though it's certainly not a standard phrase.
[This comment is no longer endorsed by its author]
Coming up with a made up word will not solve this problem. If the word describes the content of the author's stories then there will be sensory experiences that a reader can expect when reading those stories.
7
I think the idea is that the hypothetical teacher is making students memorize passwords instead of teaching the meaning of the concept.
4
post-catalytic
psycho-elemental
anti-ludic
anarcho-hegemonic
desublimational
5
"Cogno-intellectual" was the catchphrase for this when I was in school. See Abrahams et al.:
5
To see the word used spectacularly, check out this paper: www.es.ele.tue.nl/~tbasten/fun/rhetoric_logic.pdf
2
LW comments use the Markdown syntax.
-1
Was that meant to be a link?
1
It was. I can't get the 'show help' menu to pop-up, so I feel frustratingly inept right now. :)
1
Put the text you want to display in square brackets, and the URL you want to go to in regular brackets. That should do it.
1
Anti-ludic has meaning, though. It means "against playfulness". Nobody may have used it yet, but that doesn't mean that you can't combine roots to make a new and meaningful word.
4
I don't think literature has any equivalent to metasyntactic variables. Still, placeholder names might help - perhaps they are examples of "post-kadigan" literature?
-1[anonymous]
http://codepad.org/H6MaC84M
1
I think those might all be real terms.
1
I think most literature teachers I've had would ignore the question entirely and use all those terms anyway with whatever meaning they thought fits best.
5
I have no idea, I just interpreted it in an obvious way.
3
I share this interpretation, but I always figured in Eliezer's examples the hypothetical professor was so obsessed with passwords or sounding knowledgeable that they didn't bother to teach the meaning of 'post-utopian', and might even have forgotten it. Or they were teaching to the test, but if this is a college class there is no standard test, so they're following some kind of doubly-lost purpose.
Or it could be that the professor is passing down passwords they were taught as a student themselves. A word must have had some meaning when it was created, but if most people treat it as a password it won't constrain their expectations.
Also, I like that the comment system correctly interpreted my use of underbars to mean italics. I've been using that convention in plaintext for 15 years or so, glad to see someone agrees with it!
She’d underlined true and truth wherever it appeared in the essay, probably about twenty times, with a question mark beside each. She wanted to know what I meant by truth.
She should hand back the paper with the note, "What do you mean by 'mean'?"
0
If someday the vast majority of people decided that what is known as "blue" should be renamed "snarffle" then eventually it would cease to be blue. Instead it would be snarffle because that is the belief. But that doesn't change the reality that it is the wavelength 475 nm. Human beliefs determine how we interpret information, not reality.
There are some kinds of truths that don't seem to be covered by truth-as-correspondence-between-map-and-territory. (Note: This general objection is well know and is given as Objection 1 in SEP's entry on Correspondence Theory.) Consider:
- modal truths if one isn't a modal realist
- mathematical truths if one isn't a mathematical Platonist
- normative truths
Maybe the first two just argues for Platonism and modal realism (although I note that Eliezer explicitly disclaimed being a modal realist). The last one is most problematic to me, because some kinds of normative statements seem to be talking about what one should do given some assumed-to-be-accurate map, and not about the map itself. For example, "You should two-box in Newcomb's problem." If I say "Alice has a false belief that she should two-box in Newcomb's problem" it doesn't seem like I'm saying that her map doesn't correspond to the territory.
So, a couple of questions that seem open to me: Do we need other notions of truth, besides correspondence between map and territory? If so, is there a more general notion of truth that covers all of these as special cases?
If I say "Alice has a false belief that she should two-box in Newcomb's problem" it doesn't seem like I'm saying that her map doesn't correspond to the territory.
The problem with Alice's belief is that it is incomplete. It's like saying "I believe that 3 is greater than" (end of sentence).
Even incomplete sentences can work in some contexts where people know how to interpret them. For example if we had a convention that all sentences ending with "greater than" have to be interpreted as "greater than zero", then in given context the sentence "3 is greater than" makes sense, and is true. It just does not make sense outside of this context. Without context, it's not a logical proposition, but rather a proposition template.
Similarly, the sentence "you should X" is meaningful in contexts which provide additional explanation of what "should" means. For a consequentialist, the meaning of "you should" is "maximizes your utility". For a theist, it could mean "makes Deity happy". For both of them, the meaning of "should" is obvious, and within their contexts, they are right. The se...
2
At the risk of nitpicking:
"Makes Deity happy" sounds to me like a very specific interpretation of "utility", rather than something separate from it. I can't picture any context for the phrase "P should X" that doesn't simply render "X maximizes utility" for different values of the word "utility". If "make Deity happy" is the end goal, wouldn't "utility" be whatever gives you the most efficient route to that goal?
-3
Utility has a single, absolute, unexpressible meaning. To say "X gives me Y utility" is pointless, because I am making a statement about qualia, which are inherently incommunicable - I cannot describe the quale "red" to a person without a visual cortex, because that person is incapable of experiencing red (or any other colour-quale). "X maximises my utility" is implied by the statements "X maximises my deity's utility" and "maximising my deity's utility maximises my utility", but this is not the same thing as saying that X should occur (which requires also that maximisng your own utility is your objective). Stripped of the word "utility", your statement reduces to "The statement 'If X is the end goal, and option A is the best way to achieve X, A should be chosen' is tautologous", which is true because this is the definition of the word "should".
I think a more general notion of truth could be defined as correspondence between a map and any structure. If you define a structure using axioms and are referencing that structure, then you can talk about the correspondence properties of that reference. This at least cover both mathematical structures and physical reality.
3
Michael Lynch has a functionalist theory of truth (described in this book) that responds to concerns like yours. His claim is that there is a "truth role" that is constant across all domains of discourse where we talk about truth and falsity of propositions. The truth role is characterized by three properties:
1. Objectivity: The belief that p is true if and only if with respect to the belief that p, things are as they are believed to be.
2. Norm of belief: It is prima facie correct to believe that p if and only if the proposition that p is true.
3. End of inquiry: Other things being equal, true beliefs are a worthy goal of inquiry.
Lynch claims that, in different domains of discourse, there are different properties that play this truth role. For instance, when we're doing science it's plausible that the appropriate realizer of the truth role is some kind of correspondence notion. On the other hand, when we're doing mathematics, one might think that the truth role is played by some sort of theoretical coherence property. Mathematical truths, according to Lynch, satisfy the truth role, but not by virtue of correspondence to some state of affairs in our external environment. He has a similar analysis of moral truths.
I'm not sure whether Lynch's particular description of the truth role is right, but the functionalist approach (truth is a functional property, and the function can be performed by many different realizers) is very attractive to me.
0
Me too, thanks for this.
1
I think Yudkowsky is a Platonist, and I'm not sure he has a consistent position on modal realism, since when arguing on morality he seemed to espouse it: see his comment here.
I don't think that "You should two-box in Newcomb's problem." is actually a normative statement, even if it contains a "should": you can rephrase it epistemically as "If you two-box in Newcomb's problem then you will maximize your expected utility".
Therefore, if you say "Alice has a false belief that if she two-boxes in Newcomb's problem then she will maximize her expected utility" you are saying that her belief doesn't correspond to the mathematical constructs underlying Newcomb's problem. If you take the Platonist position that mathematical constructs exist as external entities ("the territory"), then yes, you are saying that her map doesn't correspond to the territory.
3
Well, sure, a utilitarian can always "rephrase" should-statements that way; to a utilitarian what "X should Y" means is "Y maximizes X's expected utility." That doesn't make "X should Y" not a normative statement, it just means that utilitarian normative statements are also objective statements about reality.
Conversely, I'm not sure a deontologist would agree that you can rephrase one as the other... that is, a deontologist might coherently (and incorrectly) say "Yes, two-boxing maximizes expected utility, but you still shouldn't do it."
-1
I think you are conflating two different types of "should" statements: moral injunctions and decision-theoretical injunctions.
The statement "You should two-box in Newcomb's problem" is normally interpreted as a decision-theoretical injunction. As such, it can be rephrased epistemically as "If you two-box in Newcomb's problem then you will maximize your expected utility".
But you could also interpret the statement "You should two-box in Newcomb's problem" as the moral injunction "It is morally right for you to two-box in Newcomb's problem". Moral injunctions can't be rephrased epistemically, at least unless you assume a priori that there exist some external moral truths that can't be further rephrased.
The utilitarianist of your comment is doing that. His actual rephrasing is "If you two-box in Newcomb's problem then you will maximize the expected universe cumulative utility". This assumes that:
* This universe cumulative utility exists as an external entity
* The statement "It is morally right for you to maximize the expected universe cumulative utility" exists as an external moral truth.
0
Thanks for the link. That does seem inconsistent.
This comment should help you understand why I disagree. Does it make sense?
2
I don't claim that all injunctions can be rephrased as epistemic statements. I claim that decision-theoretic injunctions can be rephrased as epistemic statements. Moral injunctions can't.
-2
I'm confused by your reply because the comment I linked to tried to explain why I don't think "You should two-box in Newcomb's problem" can be rephrased as an epistemic statement (as you claimed earlier). Did you read it, and if so, can you explain why you disagree with its reasoning?
ETA: Sorry, I didn't notice your comment in the other subthread where you gave your definitions of "decision-theoretic" vs "moral" injunctions. Your reply makes more sense with those definitions in mind, but I think it shows that the comment I linked to didn't get my point across. So I'll try it again here. You said earlier:
A causal decision theorist (C) and an evidential decision theorist (E) have different definitions of "maximize your expected utility", and so when C says to E "you should two-box in Newcomb's problem" he is not just saying "If you two-box in Newcomb's problem then you will maximize your expected utility according to the CDT formula" since E wouldn't care about that. So my point is that "you should two-box in Newcomb's problem" is usually not a "decision-theoretical injunction" in your sense of the phrase, but rather a normative statement as I claimed.
2
I was assuming implicitely that we were talking in the context of EDT.
In general, you can say "Two-boxing in Newcomb's problem is the optimal action for you", where the definition of "optimal action" depends on the decision theory you use.
If you use EDT, then "optimal action" means "maximizes expected utility", hence the statement above is false (that is, it is inconsistent with the axioms of EDT and Newcomb's problem).
If you use CDT, then "optimal action" means "maximizes expected utility under a causality assumption". Hence the statement above is technically true, although not very useful, since the axioms that define Newcomb's problem specifically violate the causality assumption.
So, which decision theory should you use? An answer like "you should use the decision theory that determines the optimal action without any assumption that violates the problem constraints" seems irreducible to an epistemic statement. But is that actually correct?
If you are studing actual agents, then the point is moot, since these agents already have a decision theory (in practice it will be an approximation of either EDT or CDT, or something else), but what if you want to improve yourself, or build an artificial agent?
Then you evaluate the new decision theory according to the decision theory that you already have. Then, assuming that in principle your current decision theory can be described epistemically, you can say, for instance: "A decision theory that determines the optimal action without any assumption that violates the problem constraints is optimal for me".
If you want to suggest a decision theory to somebody who is not you, you can say: "A decision theory that determines the optimal action without any assumption that violates the problem constraints is optimal for you", or, more properly but less politely: "You using a decision theory that determines the optimal action without any assumption that violates the problem constraints are optimal for me".
1
I had similar thoughts before, but eventually changed my mind. Unfortunately it's hard to convince people that their solution to some problem isn't entirely satisfactory without having a better solution at hand. (For example, this post of mine pointing out a problem with using probability theory to deal with indexical uncertainty sat at 0 points for months before I made my UDT post which suggested a different solution.) So instead of trying harder to convince people now, I think I will instead try harder to figure out a better answer by myself (and others who already share my views).
1
It seems that way to me. Specifically, in that case I think you're saying that Alice (wrongly) expects that her decision is causally independent from the money Omega put in the boxes, and as such thinks that her expected utility is higher from grabbing both boxes.
1
I don't think 2 is answered even if you say that the mathematical objects are themselves real. Consider a geometry that labels "true" everything that follows from its axioms. If this geometry is consistent, then we want to say that it is true, which implies that everything it labels as "true", is. And the axioms themselves follow from the axioms, so the mathematical system says that they're true. But you can also have another valid mathematical system, where one of those axioms is negated. This is a problem because it implies that something can be both true and not true.
Because of this, the sense in which mathematical propositions can be true can't be the same sense in which "snow is white" can be true, even if the objects themselves are real. We have to be equivocating somewhere on "truth".
5
It's easy to overcome that simply by being a bit more precise - you are saying that such and such a proposition is true in geometry X. Meaning that the axioms of geometry X genuinely do imply the proposition. That this proposition may not be true in geometry Y has nothing to do with it.
It is a different sense of true in that it isn't necessarily related to sensory experience - only to the interrelationships of ideas.
0
You are tacitly assuming that Platonists have to hold that what is formally true (proveable, derivable from axioms) is actuallty true. But a significant part of the content of Platonism is that mathematical statements are only really true if they correspond to the organisation of Plato's heaven. Platonists can say, "I know you proved that, but it isn't actually true". So there are indeed different notions of truth at play here.
Which is not to defend Platonism. The notion of a "real truth" which can't be publically assessed or agreed upon in the way that formal proof can be is quite problematical.
0
He says that counterfactuals do have a truth value, though IMO he's a bit vague about what that is (or maybe it's me who can't fully understand what he says).
If the above is true, aren't the postmodernists right?
I do wish that you would say "relativists" or the like here. Many of your readers will know the word "postmodernist" solely as a slur against a rival tribe.
Actually, "relativist" isn't a lot better, because it's still pretty clear who's meant, and it's a very charged term in some political discussions.
I think it's a bad rhetorical strategy to mock the cognitive style of a particular academic discipline, or of a particular school within a discipline, even if you know all about that discipline. That's not because you'll convert people who are steeped in the way of thinking you're trying to counter, but because you can end up pushing the "undecided" to their side.
Let's say we have a bright young student who is, to oversimplify, on the cusp of going down either the path of Good ("parsimony counts", "there's an objective way to determine what hypothesis is simpler", "it looks like there's an exterior, shared reality", "we can improve our maps"...) or the path of Evil ("all concepts start out equal", "we can make arbitrary maps", "truth is determined by politics" ...). Well, that bright young student isn't a perfectly rational being. If the advocates for Good look like they're being jerks and mocking the advocates for Evil, that may be enough to push that person down the path of Evil.
Wulky Wilkinson is the mind killer. Or so it seems to me.
6
I agree with your point about rhetoric, but I think you give post-modern thought too little credit. First of all, Sturgeon's law says 90% of everything is crap.
I can't understand why you think this statement is post-modern - or why you think it is wrong. Luminiferous Aether was possibly correct - until we tested the proposition, what basis did we have to say that ~P was better than P?
This has clear flavors of post-modernism - and is false as stated. But I think someone like Foucault would want the adjective social thrown in there a bit. Given that, the diversity of cultures throughout history is some evidence that the proposition could be true - depending on what caveats we place on / how we define "arbitrary."
Kuhn and Feyerabend have not always been clear on how anti-scientific realist they intended to be, but I think a proposition like "Scientific models are socially mediated" is plausible - unless Kuhn and Feyerabend totally screwed up their history.
Again, post-modern flavored. And again, if we add the word "social" to the front, the statement is likely true. For example, people once thought social class (nobility, peasant, merchant) was very morally relevant. Now, not so much.
-2
With the first item, "all concepts start out equal", consider that Occam's Razor says we should prefer simpler concepts.
With "we can make arbitrary maps", I don't see how adding the word "social" in there anywhere makes it any better. Although there are many different cultures, the space of possible culture-models or culture-maps is much larger still, and so if we're trying to model how a culture works we can't just pick a map arbitrarily.
Same issue applies to "truth is determined by politics". A political theory is a hypothesis about what conditions will create a given sort of society. Some political theories are better than others at such predictions.
I presume that the point with "social" is that, even if some political theories are better than others, the extent to which different theories are accepted or believed by the population at large is also strongly affected by social factors. Which, again, is an idea that has been discussed on LW a lot, and is generally accepted here...
Also, (guessing from my discussions with smart humanities people) it's saying that supposedly neutral and impartial research by scientists will be affected by a large number of (social) biases, some of them conscious, some of them unconscious, and this can have a big impact on which theory is accepted as the best and the most "experimentally tested" one. Again, not exactly a heretical belief on LW.
Ironically, I always thought that many of the posts on LW were using scientific data to show what my various humanities friends had been saying all along.
7
Particularly since many LWers believe things like:
or
0
Why is the former false?
5
Hrm?
Who said those were false? My point was that these are ideas that are popular in LW and basically true, but that most LWers don't acknowledge are post-modern in origin.
The first statement is a basic takeaway from Kuhn and Feyerabend. The second is basic History of Sexuality from Foucault.
2
Oh, sorry, didn't get your point. I think the first statement has been reinvented often, by people who read enough Kelvin quotes.
The second statement is just bizarre. Clearly many people are helped by their meds. Does feeding random psych meds to random freaks produce an increase in quality of life, or at least a wide enough spread that there's a large group that gets a stable improvement? Or are you just claiming the weaker version: symptoms make sense and are treated, but all statements of the form "patients with this set of symptoms form a cluster, and shall be labeled Noun Phrase Disorder" are false? I would claim some diagnoses are reasonable, e.g. Borderline Personality with clearly forms a cluster among bloggers who talk about their mental health. And those that aren't (a whole lotta paraphilias, and ways to cut up umbrella terms) tend to change fast anyway.
Psychology has made significant strides in response to criticism from the post-modernists. The post-modern criticism of mental health treatment is much less biting than it once was.
Still, for halo effect reasons, we should be careful.
The larger point is that Eliezer's reference to post-modernism is simply a Boo Light and deserves to be called out as such.
0
Your link does not support your claim that post-modernists had an effect.
----------------------------------------
Fubarobfusco may have a point about boo lights, but this large thread you have spawned distracts from it and thus undercuts him. In the long run, praising postmodernists may be a good approach to diffusing boo lights, but if you want to do that, make a separate post. In the short term, doing so distracts from the point. Whether postmodernists said useful things is not relevant to whether they said what Eliezer attributes to them and is not relevant to how the audience reacts to that attribution.
5
Many people can effectively be kept out of trouble and made easier for caretakers or relatives to care for via mild sedation. This is fairly clearly the function of at least a significant portion of psychiatric medication.
1[anonymous]
Systematic execution of the old guard doesn't count as scientific progress? Hmm, or does it?
3
Someone is trying to set up a strawman. Kuhn didn't advocate violent overthrow of the scientific establishment - he simply noted that generational change was an under-appreciated part of the change of scientific orthodoxy.
0[anonymous]
Someone is just trying to make a joke.
1
The prose wasn't quite as good as the joke's intent, so part of the effect was lost. Still, it made me smile, FWIW :P
-2
The difference is that post-modernists believe that something like this is true for all science and use this to justify this state of affairs in psychology, whereas LWers believe that this is not an acceptable state of affairs and should be fixed.
Edit: Also as MizedNuts pointed out, the diagnoses do try to cut reality at the joints, they just frequently fail due to social signaling interfering with seeking truth.
7
First, if physical anti-realism is true to some extent, then it is true to that extent. By contrast, if Kuhn and Feyerabend messed up the history, then physical anti-realists have no leg to stand on. People can stand what is true, for they are already enduring it.
Second, folks like Foucault were at the forefront of the argument that unstated social norm enforcement via psychological diagnosis was far worse than explicit social norm enforcement. They certainly don't argue that the current state of affairs in psychology was (or is) justifiable.
7[anonymous]
Citation appreciated. Foucault was specifically trying to improve the standards of psychiatric care.
This post is better than the simple truth and I will be linking to it more often, even though this isn't as funny.
Nice illustrations.
EDIT: Reworded in praise-first style.
The other day Yvain was reading aloud from Feser and I said I wished Feser would read The Simple Truth. I don't think this would help quite as much.
The Simple Truth sought to convey the intuition that truth is not just a property of propositions in brains, but of any system successfully entangled with another system. Once the shepherd's leveled up a bit in his craftsmanship, the sheep can pull aside the curtain, drop a pebble into the bucket, and the level in the bucket will remain true without human intervention.
0
Good point.
I also really enjoyed this post, and specifically thought that the illustrations were much nicer than what's been done before.
However, I did notice that out of all the illustrations that were made for this post, there were about 8 male characters drawn, and 0 females. (The first picture of the Sally-Anne test did portray females, but it was taken from another source, not drawn for this post like the others.) In the future, it might be a good idea to portray both men AND women in your illustrations. I know that you personally use the "flip a coin" method for gender assignment when you can, but it doesn't seem like the illustrator does (There IS a 0.3% chance that the coin flips just all came up "male" for the drawings)
The specs given to the illustrator were stick figures. I noticed the male prevalence and requested some female versions or replacement with actual stick figures.
7
In the light of the illustrations' lack of gender variety it's strange that they do have a variety of skin and hair colors.
3
Fixed.
3
I hadn't noticed about their sex, but I did notice that they all seem to be children and no adults (EDIT: except the professor in the last picture). (BTW, the character with dark hair, pale skin, red T-shirt and blue trousers doesn't obviously look masculine to me; it might as well be a female child (too young to have boobs).)
7
Thanks!
7
Ditto.
Koan answers here for:
What rule could restrict our beliefs to just propositions that can be meaningful, without excluding a priori anything that could in principle be true?
I dislike the "post utopian" example, and here's why:
Language is pretty much a set of labels. When we call something "white", we are saying it has some property of "whiteness." NOW we can discuss wavelengths and how light works, or whatnot, but 200 years ago, they had no clue. They could still know that snow is white, though. At the same time, even with our knowledge of how colors work, we can still have difficulties knowing exactly where the label "white" ends, and grey or yellow begins.
Say I'm carving up music-space. I can pretty easily classify the differences between Classical and Rap, in ways that are easy to follow. I could say that classical features a lot of instrumentation, and rap features rhythmic language, or something. But if I had lots of people spending all their lives studying music, they're going to end up breaking music space into much smaller pieces. For example, dub step and house.
Now, I can RECOGNIZE dubstep when I hear it, but if you asked me to teach you what it was, I would have difficulties. I couldn't necessarily say "It's the one that goes, like, WOPWOPWOPWOP iiinnnnnggg" if I'm a learned professor, so I'...
I think Eliezer is taking it as a given that English college professors who talk like that are indeed talking without connection to anticipated experience. This may not play effectively to those he is trying to teach, and as you say, may not even be true.
-3
In particular, "post-utopian" is not a real term so far as I know, and I'm using it as a stand-in for literary terms that do in fact have no meaning. If you think there are none of those, Alan Sokal would like to have a word with you.
There's a sense in which a lot of fuzzy claims are meaningless: for example, it would be hard for a computer to evaluate "Socrates is kind" even if the computer could easily evaluate more direct claims like "Socrates is taller than five feet". But "kind" isn't really meaningless; it would just be a lot of work to establish exactly what goes into saying "kind" and exactly where the cutoff point between "kind" and "not so kind" is.
I agree that literary critical terms are fuzzy in the same sense as "kind", but I don't think they're necessarily any more fuzzy. For example, replacing "post-utopian" with its likely inspiration "post-colonial", I don't know much about literature, but I feel pretty okay designating Salman Rushdie as "post-colonial" (since his books very often take place against the backdrop of the issues surrounding British decolonization of India) and J. K. Rowling as "not post-colonial" (since her books don't deal with issues surrounding decolonization at all.)
Likewise, even though "post-utopian" was chosen specifically to be meaningless, I can say with...
I liked your comment and have a half-formed metaphor for you to either pick apart or develop:
LW/ rationalist types tend towards hard sciences. This requires more System 2 reasoning. Their fields are like computer programs. Every step makes sense, and is understood.
Humanities tends toward more System 1 pattern recognition. This is more akin to a neural network. Even if you are getting the "right" answer, it is coming out of a black box.
Because the rationalist types can't see the algorithm, they assume it can't be "right".
Thoughts?
I like your idea and upvoted the comment, but I don't know enough about neural networks to have a meaningful opinion on it.
4
I like the idea that this comment produces in my mind. But nitpickingly, a neural network is a type of computer program. And most of the professional bollocks-talkers of my acquaintance think very hard in system-two like ways about the rubbish they spout.
It's hard to imagine a system-one academic discipline. Something like 'Professor of telling whether people you are looking at are angry', or 'Professor of catching cricket balls'....
I wonder if you might be thinking more of the difference between a computer program that one fully understands (a rare thing indeed), and one which is only dimly understood, and made up of 'magical' parts even though its top level behaviour may be reasonably predictable (which is how most programmers perceive most programs).
-3
Well, in the case of answers to questions like that in the humanities what does the word 'right' actually mean? If we say a particular author is 'post utopian' what does it actually mean for the answer to that question to be 'yes' or 'no'? It's just a classification that we invented. And like all classification groups there is a set of rules characteristics that mean that the author is either post utopian or not. I imagine it as a checklist of features which gets ticked off as a person reads the book. If all the items in the checklist are ticked then the author is post utopian. If not then the author is not.
The problem with this is that different people have different items in their checklist and differ in their opinion on how many items in the list need to be checked for the author to be classified as post utopian. You can pick any literary classification and this will be the case. There will never be a consensus on all the items in the checklist. There will always be a few points that everybody does not agree on. This makes me think that objectively speaking there is not 'absolutely right' or 'absolutely wrong' answer to a question like that.
In hard science on the other hand. There is always an absolutely right answer. If we say: "Protons and neutrons are oppositely charged." There is an answer that is right because no matter what my beliefs, experiment is the final arbiter. Nobody who follows through the logical steps can deny that they are oppositely charged without making an illogical leap.
In the literary classification, you or your neural network can go through logical steps and still arrive at an answer that is not the same for everybody.
EDIT: I meant "protons and electrons are oppositely charged" not "protons and neutrons". Sorry!
5
One: Protons and neutrons aren't oppositely charged.
Two: You're using particle physics as an example of an area where experiment is the final arbiter; you might not want to do that. Scientific consensus has more than a few established beliefs in that field that are untested and border on untestable.
1
Honestly, he'd be hard pressed to find a field that has better tested beliefs and greater convergence of evidence. The established beliefs you mention are a problem everywhere, and pretty much no field is backed with as much data as particle physics.
1
Fair enough; I had wanted to say that but don't have sufficiently intimate awareness of every academic field to be comfortable doing so. I think it works just as well to illustrate that we oughtn't confuse passing flaws in a field with fundamental ones, or the qualities of a /discipline/ with the qualities of seeking truth in a particular domain.
1
Press the Show help button to figure out how to italisize and bold and all that.
0
Was this intended to be a response to a different comment?
1
No, it's just that FluffyC used slashes to indicate that the word in the middle was to be italisized, so she probably hadn't read the help section, and I thought that reading the help section would, well, help FluffyC.
0
Oh Whoops! I mean protons and electrons! Silly mistake!
-4
I don't think that the fact that everyone having a different checklist is the point. In this perfect, hypothetical world, everyone has the same checklist.
I think that the point is that the checklist is meaningless, like having a literary genre called y-ism and having "The letter 'y' constitutes 1/26th of the text" on the checklist.
Even if we can identify y-ism with our senses, the distinction is doesn't "mean" anything. It has zero application outside of the world of y-ism. It floats.
6
That is an important point. It is not so easy to come up up with a criterion of "meaningfulness" that excludes the stuff rationalists don't like, but doens't exclude a lot of everyday terninology at the same time.
I could add that others have their own criteria of "meaningfulness". Humanities types aren't very bothered about questions like how many moons saturn has, because it doens't affect them or their society. The common factor seems to both kinds of "meaningfullness" is that they amount to "the stuff I personally consider to be worth bothering about". A concern with objective meaningfullness is still a subjective concern.
2
FWIW, the Moby Dick example is less stupid than you paint it, given the recurrence of whiteness as an attribute of things special or good in western culture - an idea that pre-dates the invention of race. I think a case could be made out that (1) the causality runs from whiteness as a special or magical attribute, to its selection as a pertinent physical feature when racism was being invented (considering that there were a number of parallel candidates, like phrenology, that didn't do so well memetically), and (2) in a world that now has racism, the ongoing presence of valuing white things as special has been both consciously used to reinforce it (cf the KKK's name and its connotations) and unconsciously reinforces it by association,
FWIW, the Moby Dick example is less stupid than you paint it, given the recurrence of whiteness as an attribute of things special or good in western culture - an idea that pre-dates the invention of race.
I can't resist. I think you should read Moby Dick. Whiteness in that novel is not used as any kind of symbol for good:
This elusive quality it is, which causes the thought of whiteness, when divorced from more kindly associations, and coupled with any object terrible in itself, to heighten that terror to the furthest bounds. Witness the white bear of the poles, and the white shark of the tropics; what but their smooth, flaky whiteness makes them the transcendent horrors they are? That ghastly whiteness it is which imparts such an abhorrent mildness, even more loathsome than terrific, to the dumb gloating of their aspect. So that not the fierce-fanged tiger in his heraldic coat can so stagger courage as the white-shrouded bear or shark.
If you want to talk about racism and Moby Dick, talk about Queequeg!
Not that white animals aren't often associated with good things, but this is not unique in western culture:
So in spring, when appears the constellation Visakha, the Bodhisatwa, under the appearance of a young white elephant of six defenses, with a head the color of cochineal, with tusks shining like gold, perfect in his organs and limbs, entered the right side of his mother, and she, by means of a dream, was conscious of the fact.
If that's your criteria, you could use some stand-in for computer science terms that have no meaning.
WMSCI, the World Multiconference on Systemics, Cybernetics and Informatics, is a computer science and engineering conference that has occurred annually since 1995. [...] WMSCI attracted publicity of a less favorable sort in 2005 when three graduate students at MIT succeeded in getting a paper accepted as a "non-reviewed paper" to the conference that had been randomly generated by a computer program called SCIgen
I think you are playing to what you assume are our prejudices.
Suppose X is a meaningless predicate from a humanities subject. Suppose you used it, not a simulacrum. If it's actually meaningless by the definition I give elsewhere in the thread, nobody will be able to name any Y such that p(X|Y) differs from p(X|¬Y) after a Bayesian update. Do you actually expect that, for any significant number of terms in humanities subjects, you would find no Y, even after grumpy defenders of X popped up in the thread? Or did you choose a made-up term so as to avoid flooding the thread with Y-proponents? If you expect people to propose candidates for Y, you aren't really expecting X to be meaningless.
The Sokal hoax only proves one journal can be tricked by fake jargon. Not that bona fide jargon is meaningless.
I'm sure there's a lot of nonsense, but "post-utopian" appears to have a quite ordinary sense, despite the lowness of the signal to noise ratio of some of those hits. A post-utopian X (X = writer, architect, hairdresser, etc.) is one who is working after, and in reaction against, a period of utopianism, i.e. belief in the perfectibility of the world by man. Post-utopians today are the people who believe that the promises of science have been found hollow, and ruin and destruction are all we have to look forward to.
We're all utopians here.
2
By this definition, wouldn't the belief that science will not lead to perfection but we can still look forward to more of what we already have (rather than ruin and destruction) be equally post-utopian?
1
Not as I see the word used, which appears to involve the sense of not merely less enthusiastic than, but turning away from. You can't make a movement on the basis of "yes, but not as sparkly".
7
Pity. "It will be kind of like it is now" is an under-utilized prediction.
6
Dunno, Futurama is pretty much entirely based on that.
What would he have to say? The Sokal Hoax was about social engineering, not semantics.
9
"Post-utopian" is a real term, and even in the absence of examples of its use, it is straightforward to deduce its (likely) meaning, since "post-" means "subsequent to, in reaction to" and "utopian" means "believing in or aiming at the perfecting of polity or social conditions". So post-utopian texts are those which react against utopianism, express skepticism at the perfectibility of society, and so on. This doesn't seem like a particularly difficult idea and it is not difficult to identify particular texts as post-utopian (for example, Koestler's Darkness at Noon, Huxley's Brave New World, or Nabokov's Bend Sinister).
So I think you need to pick a better example: "post-utopian" doesn't cut it. The fact that you have chosen a weak example increases my skepticism as to the merits of your general argument. If meaningless terms are rife in the field of English literature, as you seem to be suggesting, then it should be easy for you to pick a real one.
(I made a similar point in response to your original post on this subject.)
There is the literature professor's belief, the student's belief, and the sentence "Carol is 'post-utopian'". While the sentence can be applied to both beliefs, the beliefs themselves are quite different beasts. The professor's belief is something that carve literature space in a way most other literature professors do. Totally meaningful. The student's belief, on the other hand, is just a label over a set of authors the student have scarcely read. Going a level deeper, we can find an explanation for this label, which turns out to be just another label ("colonial alienation"), and then it stops. From Eliezer's main post (emphasis mine) :
Some literature professor lectures that the famous authors Carol, Danny, and Elaine are all 'post-utopians', which you can tell because their writings exhibit signs of 'colonial alienation'. For most college students the typical result will be that their brain's version of an object-attribute list will assign the attribute 'post-utopian' to the authors Carol, Danny, and Elaine.
- The professor have a meaningful belief.
- Unable to express it properly (it may not be his fault), gives a mysterious explanation.
- That mysterious expl
9
If that is what Eliezer meant, then it was confusing to use an example for which many people suspect that the concept itself is not meaningful. It just generates distraction, like the "Is Nixon a pacifist?" example in the original Politics is the mind-killer post (and actually,the meaningfulness of post-colonialism as a category might be a political example in the wide sense of the word). He could have used something from physics like "Heat is transmitted by convention", or really any other topic that a student can learn by rot without real understanding.
4
I don't think Eliezer meant all what I have written (edit: yep, he didn't). I was mainly analysing (and defending) the example to death, under Daenerys' proposed assumption that the belief in the professor's head is not floating. More likely, he picked something familiar that would make us think something like "yeah, if those are just labels, that's no use".¹
By the way is there any good example? Something that (i) clearly is meaningful, and (ii) let us empathise with those who nevertheless extract a floating belief out of it? I'm not sure. I for one don't empathise with the students who merely learn by rot, for I myself don't like loosely connected belief networks: I always wanted to understand.
Also, Eliezer wasn't very explicit about the distinction between a statement, embodied in text, images, or whatever our senses can process, and belief, embodied in a heap of neurons. But this post is introductory. It is probably not very useful to make the distinction so soon. More important is to realize that ideas are not floating in the void, but are embodied in a medium: paper, computers… and of course brains.
[1] We're not familiar to "post-utopianism" and "colonial alienation" specifically, but we do know the feeling generated by such literary mumbo jumbo.
2
Thank you! Your post helped me finally to understand what it was that I found so dissatisfying with the way I'm being taught chemistry. I'm not sure right now what I can do to remedy this, but thank you for helping me come to the realization.
5
If the teacher does not have a precise codification of what makes a writer "post-utopian", then how should he teach it to students?
I would say the best way is a mix of demonstrating examples ("Alice is not a post-utopian; Carol is a post-utopian"), and offering generalizations that are correlated with whether the author is a post-utopian ("colonial alienation"). This is a fairly slow method of instruction, at least in some cases where the things being studied are complicated, but it can be effective. While the student's belief may not yet be as well-formed as the professor's, I would hesitate to call it meaningless. (More specifically, I would agree denotatively but object connotatively to such a classification.) I would definitely not call the belief useless, since it forms the basis for a later belief that will be meaningful. If a route to meaningful, useful belief B goes through "meaningless" belief A, then I would say that A is useful, and that calling A meaningless produces all the wrong sorts of connotations.
2
The example assumed bad teaching based on rote learning. Your idea might actually work.
(Edit: oops, you're probably aware of that. Sorry for the noise)
9[anonymous]
To over-extend your metaphor, dubstep is electronic music with a breakbeat and certain BPM. Bassnectar described it in an inverview once as hip-hop beats at half time in breakbeat BPMs.
It's really easy to tell the difference between dubstep and house, because dubstep has a broken kick..kickSNARE beat, while house has a 4/4 kick.kick.kick.kick beat.
(Interestingly, the dubstep you seem to describe is what people who listened to earlier dubstep commonly call "brostep," and was inspired by one Rusko song ("Cockney Thug," if I remember correctly).)
The point I mean to make by this is that most concepts do have system 2 algorithms that identify them, even if most people on LW would disagree with the social groups that advance those concepts.
I have many friends and comrades that are liberal arts students, and most of the time, if they said something like "post-utopian" or "colonial alienation" they'd have a coherent system-2 algorithm for identifying which authors or texts are more or less post-utopian.
Really, I agree that this is a bad example, because there are two things going on: the students have to guess the teacher's password (which is the same as if you had Skirllex teaching MUSC 202: Dubstep Identification, and only accepted "songs with that heavy wobble bass shit" as "real dubstep, bro"), and there's an alleged unspoken conspiracy of academics to have a meaningless classifier (which is maybe the same as subgenres of hard noise music, where there truly is no difference between typical songs in each subgenre, and only artist self-identification or consensus among raters can be used as a grouping strategy).
As others have said better than me, the Sokal affair seems to be better evidence of how easy it is to publish a bad paper than it is evidence that postmodernism is a flawed field.
8
Example: an irishman arguing with a mongolian over what dragons look like.
9
When the Irishman is a painter and the Mongolian a dissatisfied customer, does their disagreement have meaning?
5
In that case, they're arguing about the wrong thing. Their real dispute is that the painting isn't what the Mongolian wanted as a result of a miscommunication which neither of them noticed until one of them had spent money (or promised to) and the other had spent days painting.
So, no, even in that situation, there's no such thing as a dragon, so they might as well be arguing about the migratory patterns of unicorns.
1
While the English profs may consistently classify writing samples as post utopian or not, the use of the label "post utopian" should be justified by the english meanings of "post" and "utopian" in some way. "Post" and "utopian" are concepts with meaning, they're not just nonsense sounds available for use as labels.
If you have no conceptual System 1 algorithm for "post utopian", and just have some consistent System 2 algorithm, it's a conceptual confusion to use compound of labels for concepts that may have nothing at all to do with your underlying System 2 defined concept.
Likely the confusion serves an intellectually dishonest purpose, as in euphemism. When you see this kind of nonsense, there is some politically motivated obfuscation nearby.
A set of beliefs is not like a bag of sand, individual beliefs unconnected with each other, about individual things. They are connected to each other by logical reasoning, like a lump of sandstone. Not all beliefs need to have a direct connection with experience, but as long as pulling on the belief pulls, perhaps indirectly, on anticipated experience, the belief is meaningful.
When a pebble of beliefs is completely disconnected from experience, or when the connection is so loose that it can be pulled around arbitrarily without feeling the tug of experience, then we can pronounce it meaningless. The pebble may make an attractive paperweight, with an intricate structure made of elements that also occur in meaningful beliefs, but that's all it can be. Music of the mind, conveying a subjective impression of deep meaning, without having any.
For the hypothetical photon disappearing in the far-far-away, no observation can be made on that photon, but we have other observations leading to beliefs about photons in general, according to which they cannot decay. That makes it meaningful to say that the far away photon acts in the same way. If we discovered processes of photon decay, it would still be meaningful, but then we would believe it could be false.
4
Interesting idea. But how did you know how to phrase your original beliefs about photons? You could just have easily decided to describe photons as "photons obey Maxwell's equations up to an event horizon and case to exist outside of it". You could then add other beliefs like "nothing exists outside of the event horizon" which are incompatible with the photon continuing to exist.
In other words, your beliefs cannot afford to be independent of one another, but you could build two different belief systems, one in which the photon continues to exist and one in which it does not, that make identical predictions about experiences. Is it meaningful to ask which of these belief systems is true?
5
Systems of belief are more like a lump of sandstone than a pile of sand, but they are also more like a lump of sandstone, a rather friable lump, than a lump of marble. They are not indissoluble structures that can be made in arbitrary shapes, the whole edifice supported by an attachment at one point to experience.
Experience never brought hypotheses such as you suggest to physicists' attention. The edifice as built has no need of it, and it cannot be bolted on: it will just fall off again.
2
But these hypotheses have just be brought to our attention - just now. In fact the claim that these hypotheses produce indistinguishable physics might even be useful. If I want to simulate my experiences, I can save on computational power by knowing that I no longer have to keep track of things that have gone behind an event horizon. The real question is why the standard set of beliefs should be more true or meaningful than this new one. A simple appeal to what physicists have so far conjectured is not in general sufficient.
0
Which meaningful beliefs to consider seriously is an issue separate from the original koan, which asks which possible beliefs are meaningful. I think we are all agreeing that a belief about the remote photon's extinction or not is a meaningful one.
0
I don't see how you can claim that the belief that the photon continues to exist is a meaningful belief without also allowing the belief that the photon does not continue to exist to be a meaningful belief. Unless you do something along the lines of taking Kolmogorov complexity into account, these beliefs seem to be completely analogous to each other. Perhaps to phrase things more neutrally, we should be asking if the question "does the photon continue to exist?" is meaningful. On the one hand, you might want to say "no" because the outcome of the question is epiphenomenal. On the other hand, you would like this question to be meaningful since it may have behavioral implications.
0
They're both meaningful. There are reasons to reject one of them as false, but that's a separate issue.
0
OK. I think that I had been misreading some of your previous posts. Allow me the rephrase my objection.
Suppose that our beliefs about photons were rewritten as "photons not beyond an event horizon obey Maxwell's Equations". Making this change to my belief structure now leaves beliefs about whether or not photons still exist beyond an event horizon unconnected from my experiences. Does the meaningfulness of this belief depend on how I phrase my other beliefs?
Also if one can equally easily produce belief systems which predict the same sets of experiences but disagree on whether or not the photon exists beyond the event horizon, how does this belief differ from the belief that Carol is a post-utopian?
0
Dunno about “meaningful”, but the model with lower Kolmogorov complexity will give you more bang for the buck.
2
Your view reminds me of Quine's "web of belief" view as expressed in "Two Dogmas of Empiricism" section 6:
Quine doesn't use Bayesian epistemology, unfortunately because I think it would have helped him clarify and refine his view.
One way to try to flesh this intuition out is to say that some beliefs are meaningful by virtue of being subject to revision by experience (i.e. they directly pay rent), while others are meaningful by virtue of being epistemically entangled with beliefs that pay rent (in the sense of not being independent beliefs in the probabilistic sense). But that seems to fail because any belief connected to a belief that directly pays rent must itself be subject to revision by experience, at least to some extent, since if A is entangled with B, an observation which revises P(A) typically revises P(B), however slightly.
Before reading other answers, I would guess that a statement is meaningful if it is either implied or refuted by a useful model of the universe - the more useful the model, the more meaningful the statement.
0[anonymous]
This is incontrovertibly the best answer given so far. My answer was that a proposition is meaningful iff an oracle machine exists that takes as input the proposition and the universe, outputs 0 if the proposition is true and outputs 1 if the proposition is false. However, this begs the question, because an oracle machine is defined in terms of a "black box".
0
Looking at Furslid's answer, I discovered that my definition is somewhat ambiguous - a statement may be implied or refuted by quite a lot of different kinds of models, some of which are nearly useless and some of which are anything but, and my definition offers no guidance on the question of which model's usefulness reflects the statement's meaningfulness.
Plus, I'm not entirely sure how it works with regards to logical contradictions.
0[anonymous]
Where Recursive Justification Hits Bottom and its comment thread should be interesting to you.
In the end, we have to rely on the logical theory of probability (as well as standard logical laws, such as the law of noncontradiction). There is no better choice.
Using Bayes' theorem (beginning with priors set by Occam's Razor) tells you how useful your model is.
5
I think I was unclear. What I was considering was along the following lines:
What occurred to me just now, as I wrote out the example, is the idea of simplicity. If you penalize models that add complexity without addition of practical value, the professor's list will be rapidly cut from almost any model more general than "what answer will receive a good grade on this professor's tests?"
If a person with access to the computer simulating whichever universe (or set of universes) a belief is about could in principle write a program that takes as input the current state of the universe (as represented in the computer) and outputs whether the belief is true, then the belief is meaningful.
(if the universe in question does not run on a computer, begin by digitizing your universe, then proceed as above)
That has the same problem as atomic-level specifications that become false when you discover QM. If the Church-Turing thesis is false, all statements you have specified thus become meaningless or false. Even using a hierarchy of oracles until you hit a sufficient one might not be enough if the universe is even more magical than that.
6
But that's only useful if you make it circular.
Taking you more strictly at your word than you mean it the program could just return true for the majority belief on empirically non-falsifiable questions. Or it could just return false on all beliefs including your belief that that is illogical. So with the right programs pretty much arbitrary beliefs pass as meaningful.
You actually want it to depend on the state of the universe in the right way, but that's just another way to say it should depend on whether the belief is true.
2
That's a problem with all theories of truth, though. "Elaine is a post-utopian author" is trivially true if you interpret "post-utopian" to mean "whatever professors say is post-utopian", or "a thing that is always true of all authors" or "is made out of mass".
To do this with programs rather than philosophy doesn't make it any worse.
I'm suggesting is that there is a correspondence between meaningful statements and universal computer programs. Obviously this theory doesn't tell you how to match the right statement to the right computer program. If you match the statement "snow is white" to the computer program that is a bunch of random characters, the program will return no result and you'll conclude that "snow is white" is meaningless. But that's just the same problem as the philosopher who refuses to accept any definition of "snow", or who claims that snow is obviously black because "snow" means that liquid fossil fuel you drill for and then turn into gasoline.
If your closest match to "post-utopian" is a program that determines whether professors think someone is post-utopian, then you can either conclude that post-utopian literally means "something people call post-utopian" - which would probably be a weird and nonstandard word use the same way using "snow" to mean "oil" would be nonstandard - or that post-utopianism isn't meaningful.
0
Yeah, probably all theories of truth are circular and the concept is simply non-tabooable. I agree your explanation doesn't make it worse, but it doesn't make it better either.
1
Doesn't this commit you to the claim that at least some beliefs about whether or not a particular Turing machine halts must be meaningless? If they are all meaningful and your criterion of meaningfulness is correct, then your simulating computer solves the halting problem. But it seems implausible that beliefs about whether Turing machines halt are meaningless.
0
Input->Black box->Desired output. "Black box" could be replaced with"magic." How would your black box work in practice?
0
That doesn't help us decide whether there are stars outside the cosmological horizon.
7
I feel like writing a more intelligent reply than "Yes it does", so could you explain this further?
0
Suppose we are not living in a simulation. We are to digitize our universe. Do we make our digitization include stars outside the cosmological horizon? By what principle do we decide?
(I suppose you could be asking us to actually digitize the universe, but we want a principle we can use today.)
0
Well, if the universe actually runs on a computer, then presumably that computer includes data for all stars, not just the ones that are visible to us.
If the universe doesn't run on a computer, then you have to actually digitize the universe so that your model is identical to the real universe as if it were on a computer, not stop halfway when it gets too hard or physically impossible.
I don't think any of these principles will actually be practical. Even the sense-experience principle isn't useful. It would classify "a particle accelerator the size of the Milky Way would generate evidence of photinos" as meaningful, but no one is going to build a particle accelerator the size of the Milky Way any more than they are going to digitize the universe. The goal is to have a philosophical tool, not a practical plan of action.
3
Oh, I didn't express myself clearly in the last paragraph of the grandparent. Don't worry, I'm not trying to demand any kind of practical procedure. I think we're on the same page. However:
I don't think we can really say that in general. Perhaps if the computer stored the locations and properties of stars in an easy-to-understand way, like a huge array of floating-point numbers, and we looked into the computer's memory and found a whole other universe's worth of extra stars, with spatial coordinates that prevent us from ever interacting with them, then we would be comfortable saying that those stars exist but are invisible to us.
But what if the computer compresses star location data, so the database of visible stars looks like random bits? And then we find an extra file in the computer, which is never accessed, and which is filled with random bits? Do we interpret those as invisible stars? I claim that there is no principled, objective way of pointing to parts of a computer's memory and saying "these bits represent stars invisible to the simulation's inhabitants, those do not".
I'm suspicious of the phrase "identical to the real universe as if it were on a computer". It seems like a black box. Suppose we commission a digital model of this universe, and the engineer in charge capriciously programs the computer to delete information about any object that passes over the cosmological horizon. But they conscientiously program the computer to periodically archive snapshots of the state of the simulation. It might look like this model does not contain spaceships that have passed over the cosmological horizon. But the engineer points out that you can easily extrapolate the correct location of the spaceship from the archived snapshots — the initial state and the laws of physics uniquely determine the present location of the spaceship beyond the cosmological horizon, if it exists. The engineer claims that the simulation actually does contain the spaceship outside the co
0
Why should it if its purpose is to simulate reality for humans? What's wrong with a version of The Truman Show?
0
Because since everything would be a simulation, "all stars" would be identical in meaning with "all stars that are being simulated" and with "all stars for which the computer includes data".
2
In a Truman Show situation, the simulators would've shown us white pin-pricks for thousands of years, and then started doing actual astrophysics simulations only when we got telescopes.
-4
A variant of Löb's theorem, isn't it?
Edit: Downvoted because the parallels are too obvious, or because the comparison seems too contrived? "E"nquiring minds want to know ...
For a belief to be meaningful you have to be able to describe evidence that would move your posterior probability of it being true after a Bayesian update.
This is a generalization of falsifiability that allows, for example, indirect evidence pertaining to universal laws.
0
How about basic logical statements? For example: If P, then P. I think that belief is meaningful, but I don't think I could coherently describe evidence that would make me change it's probability of being true.
0
Possible counterexample: "All possible mathematical structures exist."
1
You'd have to define "exist", because mathematical structures in themselves are just generalized relations that hold under specified constraints. And once you defined "exist", it might be easier to look for Bayesian evidence - either for them existing, or for a law that would require them to exist.
As a general thing, my definition does consider under-defined assertions meaningless, but that seems correct.
0
Yeah, I'm not really sure how to interpret "exist" in that statement. Someone that knows more about Tegmark level IV than I do should weigh in, but my intuition is that if parallel mathematical structures exist that we can't, in principle, even interact with, it's impossible to obtain Bayesian evidence about whether they exist.
0
If we couldn't, even in principle, find any evidence that would make the theory more likely or less, then yeah I think that theory would be correctly labeled meaningless.
But, I can immediately think of some evidence that would move my posterior probability. If all definable universes exist, we should expect (by Occam) to be in a simple one, and (by anthropic reasoning) in a survivable one, but we should not expect it to be elegant. The laws should be quirky, because the number of possible universes (that are simple and survivable) is larger than the subset thereof that are elegant.
0
Why? That assumes the universes are weighted by complexity, which isn't true in all Tegmark level IV theories.
8
Consider "Elaine is a post-utopian and the Earth is round" This statement is meaningless, at least in the case where the Earth is round, where it is equivalent to "Elaine is a post-utopian." Yet it does constrain my experience, because observing that the Earth is flat falsifies it. If something like this came to seem like a natural proposition to consider, I think it would be hard to notice it was (partly) meaningless, since I could still notice it being updated.
This seems to defeat many suggestions people have made so far. I guess we could say it's not a real counterexample, because the statement is still "partly meaningful". But in that case it would be still be nice if we could say what "partly meaningful" means. I think that the situation often arises that a concept or belief people throw around has a lot of useless conceptual baggage that doesn't track anything in the real world, yet doesn't completely fail to constrain reality (I'd put phlogiston and possibly some literary criticism concepts in this category).
My first attempt is to say that a belief A of X is meaningful to the extent that it (is contained in / has an analog in / is resolved by) the most parsimonious model of the universe which makes all predictions about direct observations that X would make.
2
A solution to that particular example is already in logic - the statements "Elaine is a post-utopian" and "the Earth is round" can be evaluated separately, and then you just need a separate rule for dealing with conjunctions.
5
For every meaningful proposition P, an author should (in theory) be able to write coherently about a fictional universe U where P is true and a fictional universe U' where P is false.
7
I thought Eliezer's story about waking up in a universe where 2+2 seems to equal 3 felt pretty coherent.
edit: It seems like the story would be less coherent if it involved detailed descriptions of re-deriving mathematics from first principles. So perhaps ArisKatsaris' definition leaves too much to the author's judgement in what to leave out of the story.
6
I think that it's a good deal more subtle than this. Eliezer described a universe in which he had evidence that 2+2=3, not a universe in which 2 plus 2 was actually equal to 3. If we talk about the mathematical statement that 2+2=4, there is actually no universe in which this can be false. On the other hand in order to know this fact we need to acquire evidence of it, which, because it is a mathematical truth, we can do without any interaction with the outside world. On the other hand if someone messed with your head, you could acquire evidence that 2 plus 2 was 3 instead, but seeing this evidence would not cause 2 plus 2 to actually equal 3.
4
On the contrary. Imagine a being that cannot (due to some neurological quirk) directly percieve objects - it can only percieve the spaces between objects, and thus indirectly deduce the presence of the objects themselves. To this being, the important thing - the thing that needs to be counted and to which a number is assigned - is the space, not the object.
Thus, "two" looks like this, with two spaces: 0 0 0
Placing "two" next to "two" gives this: 0 0 0 0 0 0
Counting the spaces gives five. Thus, 2+2=5.
2
I think you misunderstand what I mean by "2+2=4". Your argument would be reasonable if I had meant "when you put two things next to another two things I end up with four things". On the other hand, this is not what I mean. In order to get that statement you need the additional, and definitely falsifiable statement "when I put a things next to b things, I have a+b things".
When I say "2+2=4", I mean that in the totally abstract object known as the natural numbers, the identity 2+2=4 holds. On the other hand the Platonist view of mathematics is perhaps a little shaky, especially among this crowd of empiricists, so if you don't want to accept the above meaning, I at least mean that "SS0+SS0=SSSS0" is a theorem in Peano Arithmetic. Neither of these claims can be false in any universe.
2
I think I understand what CCC means by the being that perceives spaces instead of objects - Peano Arithmetic only exists because it is useful for us, human beings, to manipulate numbers that way. Given a different set of conditions, a different set of mathematical axioms would be employed.
0
Peano Arithmetic is merely a collection of axioms (and axiom schema), and inference laws. It's existence is not predicated upon its usefulness, and neither are its theorems.
I agree that the fact that we actually talk about Peano Arithmetic is a consequence of the fact that it (a) is useful to us (b) appeals to our aesthetic sense. On the other hand, although the being described in CCC's post may not have developed Peano's axioms on their own, once they are informed of these axioms (and modus ponens, and what it means for something to be a theorem), they would still agree that "SS0+SS0=SSSS0" in Peano Arithmetic.
In summary, although there may be universes in which the belief "2+2=4" is no longer useful, there are no universes in which it is not true.
2
I freely concede that a tree falling in the woods with no-one around makes acoustic vibrations, but I think it is relevant that it does not make any auditory experiences.
In retrospect, however, backtracking to the original comment, if "2+2=4" were replaced by "not(A and B) = (not A) or (not B)", I think my argument would be nearly untenable. I think that probably suffices to demonstrate that ArisKatsaris's theory of meaningfulness is flawed.
2
How is it relevant? CCC was arguing that "2+2=4" was not true in some universes, not that it wouldn't be discovered or useful in all universes. If your other example makes you happy that's fine, but I think it would be possible to find hypothetical observers to whom De Morgan's Law is equally useless. For example, the observer trapped in a sensory deprivation chamber may not have enough in the way of actual experiences for De Morgan's Law to be at all useful in making sense of them.
3
In my opinion, saying "2+2=4 in every universe" is roughly equivalent to saying "1.f3 is a poor chess opening in every universe" - it's "true" only if you stipulate a set of axioms whose meaningfulness is contingent on facts about our universe. It's a valid interpretation of the term "true", but it is not the only such interpretation, and it is not my preferred interpretation. That's all.
2
If this is the case, then I'm confused as to what you mean by "true". Let's consider the statement "In the standard initial configuration in chess, there's a helpmate in 2". I imagine that you consider this analogous to your example of a statement about chess, but I am more comfortable with this one because it's not clear exactly what a "poor move" is.
Now, if we wanted to explain this statement to a being from another universe, we would need to taboo "chess" and "helpmate" (and maybe "move"). The statement then unfolds into the following:
"In the game with the following set of rules... there is a sequence of play that causes the game to end after only two turns are taken by each player"
Now this statement is equivalent to the first, but seems to me like it is only more meaningful to us than it is to anyone else because the game it describes matches a game that we, in a universe where chess is well known, have a non-trivial probability of ever playing. It seems like you want to use "true" to mean "true and useful", but I don't think that this agrees with what most people mean by "true".
For example, there are infinitely many true statements of the form "A+B=C" for some specific integers A,B,C. On the other hand, if you pick A and B to be random really large numbers, the probability that the statement in question will ever be useful to anyone becomes negligible. On the other hand, it seems weird to start calling these statements "false" or "meaningless".
2
You're right, of course. To a large extent my comment sprung from a dislike of the idea that mathematics possesses some special ontological status independent of its relevance to our world - your point that even those statements which are parochial can be translated into terms comprehensible in a language fitted to a different sort of universe pretty much refutes that concern of mine.
0
I suppose it depends on how stict you are about what "coherently" means. A fictional universe is not the same as a possible universe and you pobably could write about a universe where you put two apples next to two other apples and then count five apples.
-1
Hmm, I get your point, upvoting -- but I'm not sure that "2+2=4" is meaningful in the same sense that "Bob already had 2 apples and bought 2 more apples, he was now in possession of 4 apples" is meaningful.
To the extent that 2+2=4 is just a matter of extending mathematical definitions from Peano Arithmetic, it's as meaningful as saying 1=1 -- less a matter of beliefs, and more of a matter of definitions. And as far as it represents real events occurring, we can indeed imagine surreal fictional universes where if you buy two apples when you have already two apples, you end up in possession of five or six or zero apples...
4[anonymous]
A variation on this question "what rule could restrict our beliefs to just propositions that can be decided, without excluding a priori anything true?" is known to hopeless in a strong sense.
Incidentally I think the phrase "in principle" isn't doing any work in your koan.
4
Meaningful seems like a odd word to choose, as it contains the answer itself. What rule restricts our beliefs to just propositions that can be meaningful? Why, we could ask ourselves if the proposition has meaning.
The "atoms" rule seems fine, if one takes out the word "atoms" and replaces it with "state of the universe," with the understanding that "state" includes both statics and dynamics. Thus, we could imagine a world where QM was not true, and other physics held sway- and the state of that world, including its dynamics, would be noticeably different than ours.
And, like daenerys, I think the statement that "Elaine is a post-utopian" can be meaningful, and the implied expanded version of it can be concordant with reality.
[edit] I also wrote my koan answers as I was going through the post, so here's 1:
And 2:
2
I very much like your response to (1) - I think the point about having access to a common universe makes it very clear.
3
Beliefs must pay rent.
1
Insufficient: the colony ship leaves no evidence.
0
How about an expanded version: if we could be a timeless spaceless perfect observer of the universe(s), what evidence would we expect to see?
-2
Can you guarantee that a TSPO wouldn't see epiphenomenal consciousness?
-2
Well, no. How is that different from epiphenomenal spaceships? Our modal predicts spaceships but no p-zombies.
2[anonymous]
I suspect that, if we are born, we already have a first model of physics, a few built-in axioms. As we grow older, we acquire beliefs that are only recursive applications and elaborations of these axioms.
I would say that, if a belief can be reduced to this lowest level of abstraction, it is a meaningful belief.
2
Proposition p is meaningful relative to the collection of possible worlds W if and only if there exist w, w' in W such that p is true in the possible world w and false in the possible world w'.
Then the question become: to be able to reason in all generality what collection of possible worlds should one use?
That's a very hard question.
2
[deleted]
0
They are truisms - in principle they are statements that are entirely redundant as one could in principle work out the truth of them without being told anything. However, principle and practice are rather different here - just because we could in principle reinvent mathematics from scratch doesn't mean that in practice we could. Consequently these beliefs are presented to us as external information rather than as the inevitable truisms they actually are.
2
"God's-eye-view" verificationism
A proposition P is meaningful if and only if P and not-P would imply different perceptions for a hypothetical entity which perceives all existing things.
(This is not any kind of argument for the actual existence of a god. Downvote if you wish, but please not due to that potential misunderstanding.)
0
Doesn't that require such an entity to be logically possible?
0
No, in fact it works better on the assumption that there is no such entity.
If it could be an existing entity, then we could construct a paradoxical proposition, such as P="There exists an object unperceived by anything.", which could not be consistently evaluated as meaningful or unmeaningful. Treating a "perceiver of all existing things" as a purely hypothetical entity--a cognitive tool, not a reality--avoids such paradoxes.
2
Huh? We're talking past each other here.
If there's an all-seeing deity, P is well-formed, meaningful, and false. Every object is perceived by the deity, including the deity itself. If there's no all-seeing deity, the deity pops into hypothetical existence outside the real world, and evaluates P for possible perceiving anythings inside the real world; P is meaningful and likely true.
But that's not what I was talking about. I'm talking about logical possibility, not existence. It's okay to have a theory that talks about squares even though you haven't built any perfect squares, and even if the laws of physics forbid it, because you have formal systems where squares exist. So you can ask "What is the smallest square that encompasses this shape?", with a hypothetical square. But you can't ask "What is the smallest square circle that encompasses this shape?", because square circles are logically impossible.
I'm having a hard time finding an example of an impossible deity, not just a Turing-underpowered one, or one that doesn't look at enough branches of a forking system. Maybe a universe where libertarian free will is true, and the deity must predict at 6AM what any agent will do at 7AM - but of course I snuck in the logical impossibility by assuming libertarian free will.
2
Oh, oops. My mental model was this: Consider an all-perceiving entity (APE) such that, for all actually existing X, APE magically perceives X. That's all of the APE's properties -- I'm not talking about classical theism or the God of any particular religion -- so it doesn't look to me like there are logical problems.
Mostly agreed. But that's not the GEV verificationism I suggested. The above paragraph takes the form "Evaluate P given APE" and "Evaluate P given no-APE". My suggestion is the reverse; it takes the form "Evaluate APE's perceptions given P" and "Evaluate APE's perceptions given not-P". If the great APE counts as a real thing, what would its set of perceptions be given that there exists an object unperceived by anything? That's simply to build a contradiction: APE sees everything, and there's something APE doesn't see. But if the all-perceiving entity is assumed not to be a real thing, the problem goes away.
2
Propositions must be able in principle to be connected to a state of how the world could-be, and this connection must be durable over alternate states of basic world identity. That is to say, it should be possible to simulate both states in which the proposition is true, and states in which it is not.
2
I don't think there can be any such rule.
2
Internal consistency. Propositions must be non self-contradictory. If a proposition is a conjunction of multiple propositions, then those propositions must not contradict each other.
2
I think the condition is necessary but not sufficient. How would it deal with the post-utopian example in the article text?
2
When we try to build a model of the underlying universe, what we're really talking about it is trying to derive properties of a program which we are observing (and a component of), and which produces our sense experiences. Probably quite a short program in its initial state, in fact (though possibly not one limited by the finite precision of traditional Turing Machines).
So, that gives us a few rules that seem likely to be general: the underlying model must be internally consistent and mathematically describable, and must have a total K-complexity less than the amount of information in the observable universe (or else we couldn't reason about it).
So the question to ask is really "can I imagine a program state that would make this proposition true, given my current beliefs about my organization of the program?"
This is resilient to the atoms / QM thing, at least, as you can always change the underlying program description to better fit the evidence.
Although, in practice, most of what intelligent entities do can more precisely be described as 'grammar fitting' than 'program induction.' We reason probabalistically, essentially by throwing heuristics at a wall to see what offers marginal returns on predicting future sense impressions, since trying to guess the next word in a sentence by reverse-deriving the original state of the universe-program and iterating it forwards is not practical for most people. That massive mess of semi-rational, anticipatorially-justified rules of thumb is what allows us to reason in the day to day.
So a more pragmatic question is 'how does this change my anticipation of future events?' or 'What sense experiences do I expect to have differently as a result of this belief?'
It is only when we seek to understand more deeply and generally, or when dealing with problems of things not directly observable, that it is practical to try to reason about the actual program underlying the universe.
1
beliefs are subsets of the set of all universes, and meaningful beliefs are proper subsets.
corollary: we can get an equivalence relation on beliefs this way
did i get it right
1
I'm pleased to find this post and community; the writing is thoughtful and challenging. I'm not a philosopher, so some of the post waltzes off the edge of my cognitive dance floor, yet without stumbling or missing a beat. Proposing a rule to restrict belief seems problematic; who will enforce the restriction and how will bear on the outcome being "just." So, the only just enforcer can be the individual believer. Perhaps the rule might pertain to the intersection of belief and action: beliefs may not cause actions that limit others' freedom or well-being. Person A believes the sky is blue. Person B complains that person A's belief limits their ability to believe that the sky is green. But person B's complaint is out of bounds, as it's based on B's desire for unanimity, a desire that limits others' freedom. Hmm.
1
For some reason, I did not find this option here (perhaps it is implied somewhere in the chains): a statement makes sense if, in principle, it is possible to imagine its sensory results in detail. Depends on whether Russell's teapot makes sense, and also suggests that 2+2=3 doesn't make sense.
1
Restrict propositions to observable references? (Or have a rule about falsifiablility?)
The problem with the observable reference rule is that sense can be divorced from reference and things can be true (in principle) even if un-sensed or un-sensable. However, when we learn language we start by associating sense with concrete reference. Abstractions are trickier.
It is the case that my sensorimotor apparatus will determine my beliefs and my ability to cross-reference my beliefs with other similar agents with similar sensorimotor apparatus will forge consensus on propositions that are meaningful and true.
Falsifiability is better. I can ask another human is Orwell post-Utopian? They can say 'hell no he is dystopian'... But if some say yes and some say no, it seems I have an issue with vagueness which I would have to clarify with some definition of criteria for post-Utopian and dystopian.
Then once we had clarity of definition we could seek evidence in his texts. A lot of humanities texts however just leave observable reference at the door and run amok with new combinations of sense. Thus you get unicorns and other forms of fantasy...
1
All the propositions must be logical consequences of a theory that predicts observation, once you've removed everything you can from the theory without changing its predictions, and without adding anything.
1
It seems to me that we at least have to admit two different classes of proposition:
1) Propositions that reflect or imply an expectation of some experiences over others. Examples include the belief that the sky is blue, and the belief that we experience the blueness of the sky mediated by photons, eyes, nerves, and the brain itself.
2) Propositions that do not imply a prediction, but that we must believe in order to keep our model of the world simple incomprehensible. An example of this would be the belief that the photon continues to exist after taxes outside of our light cone.
1
Solomonoff induction! Just kidding.
0
If I, given a universal interface to a class of sentient beings, but without access to that being's language or internal mind-state, could create an environment for each possible truth value of the statement, where any experiment conducted by a being of that class upon the environment would reflect the environment's programmed truth value of the statement, and that being could form a confidence of belief regarding the statement which would be roughly uniform among beings of that class and generally leaning in the direction of the programmed truth value, then the statement has meaning.
In other words, I put on my robe and wizard's cap, and you put on your haptic feedback vest and virtual reality helmet, and you tell me whether Elaine is a Post-Utopian.
This should cover propositions whose truth-value might not be knowable by us within our present universe if we can craft the environment such that it is knowable via the interface to the observer. e.g. hyperluminal messaging / teleportation / "pause" mode / "ghost" mode, debug HUDs, etc.
0[anonymous]
Explicitly assuming realism and reductionism. I think.
A meaningful statement is one that claims the "actual reality" lies within a particular well-defined subset of possible worlds, where each possible world is a complete and concrete specification of everything in that universe, to the highest available precision, at the lowest possible level of description, in that universes own ontology.
Of course, superhuge uncomputable subsets of possible worlds are not practically useful, so we compress by talking about concepts (like "white", "snow", "5", "post-utopian"), among other things. Unfortunately, once we get into turing-complete compression, we can construct programs (concepts) that do all sorts of stupid stuff (like not halt). Concepts need to be portable between ontologies. This might sink this whole idea.
For example, "snow is white" says the One True Reality is within the (unimaginably huge) subset of possible worlds where the substructures that the "snow" concept matches are also matched by the "white" concept.
For example "2 + 2 = 5" refers to the subset of possible worlds where the concept generated by the application of the higher-order concept "+" to "2" and "2" will match everything matched by "5". (I unpacked "=" to "concepts match same things", but you don't have to) There's something really neat about these abstract concepts, but they don't seem fundamentally different from other ones.
TL;DR: So the rule is "your beliefs should be specified by a probability distribution over exact possible worlds", and I don't know of a compression language for possible world subsets that can't express meaningless concepts (and it probably isn't worth it to look for one).
0
"A statement can be meaningful if a test can be constructed that will return only one result, in all circumstances, if the statement is true."
Consider the satement: If I throw an object off this cliff, then the object will fall. The test is obvious; I can take a wide variety of objects (a bowling ball, a rock, a toy car, and a set of music CDs by ) and throw them off the cliff. I can then note that all of them fall, and therefore improve the probability that the statement is true. I can then take one final object, a helium balloon, and throw it off the cliff; as the balloon rises, however, I have therefore shown that the statement is false. (A more correct version would be "if I throw a heavier-than-air object off this cliff, then the object will fall." It's still not completely true yet - a live pigeon is heavier than air - but it's closer).
By this test, however, the statement "Carol is a post-utopian author" is meaningful, as long as there exist some features which are the features of post-modern authors (the features do not need to be described, or even known, as long as their existence can be proven - repeatable, correct classification by a series of artificial neural networks would prove that such features exist).
0
Here's my first swing at it: A proposition is meaningful if it constrains the predicted observations of any theoretically possible observer.
This way, the proposition "the unmanned starship will not blink out of existence when it leaves my light cone" is meaningful because it's possible that there might potentially be an observer nearby who observes the starship not disappear.
On the other hand, the statement "The position of this particle is exactly X and its momentum exactly P" is not meaningful under this rule, and that's a feature.
0
Taboo "theoretically possible".
0
Hm, how about: "[...] of any observer which our best current theory of how minds work says could exist".
So for example, a statement along the lines of "a ghost watches and sees whether or not Mars continues to exist when it passes behind the Sun from Earth's perspective" would have been meaningful a long time ago, but is not meaningful for people today who know a little about brains.
This also means that a proposition may be meaningful only because the proposer is ignorant.
0
Taboo "could". Basically, counter-factual surgery is a lot trickier than you seem to think.
0
There aren't many threads where I'd let that pass. This is one of them.
0
My $0.02:
A proposition P is meaningful to an observer O to the extent that O can alter its expectations about the world based on P.
This doesn't a priori exclude anything that could be true, although for any given observer it might do so. As it should. Not every true proposition is meaningful to me, for example, and some true propositions that are meaningful to me aren't meaningful to my mom.
Of course, it doesn't necessarily exclude things that are false, either. (Nor should it. Propositions can be meaningful and false.)
For clarity, it's also perhaps worth distinguishing between propositions and utterances, although the above is also true of meaningful utterances.
0
Maps are models of the territory. And the usefulness of them is often that they make predictions about parts of the territory I haven't actually seen yet, and may have trouble getting to at all. The Sun will come up in the morning. There isn't a leprachaun colony living a mile beneath my house. There aren't any parts of the moon that are made of cheese.
I have no problem saying that these things are true, but they are in fact extrapolations of my current map into areas which I haven't seen and may never see. These statements don't meaningfully stand alone, they arise out of extrapolating a map that checks out in all sorts of other locations which I can check. One can then have meaningful certainty about the zones that haven't yet been seen.
How does one extrapolate a map? In principle I'd say that you should find the most compressible form - the form that describes the territory without adding extra 'information' that I've assumed from someplace else. The compressed form then leads to predictions over and above the bald facts that go into it.
The map should match the territory in the places you can check. When I then make statements that something is "true", I'm making assertions about what the world is like, based on my map. As far as English is concerned, I don't need absolute certainty to say something is true, merely reasonable likelihood.
Hence the photon. The most compressible form of our description of the universe is that the parts of space that are just beyond visibility aren't inherently different from the parts we can see. So the photon doesn't blink out over there, because we don't see any such blinking out over here.
0[anonymous]
If by "meaningful" you mean "either true or false" and by "meaningless" you mean "neither true nor false", then a Platonist and a formalist would disagree about the meaningfulness of the continuum hypothesis. Since I don't know any knockdown argument for either Platonism or formalism, I defy everyone who claims to have a crisp answer to your question, including possibly you.
0
OK. Here's my best shot at it.
Firstly, I don't really like the wording of the Koan. I feel like a more accurate statement of the fundamental problem here is "What rule could restrict our beliefs to propositions that we can usefully discuss whether or not they are true without excluding any statements for which we would like be base our behavior on whether or not they are true." Unfortunately, on some level I do not believe that there is a satisfactory answer here. Though it is quite possible that the problem is with my wanting to base my behavior on the truth of statements whose truth cannot be meaningfully discussed.
To start with, let's talk about the restriction about restricting to statements for which we can meaningfully discuss whether or not they are true. Given the context of the post this is relatively straightforward. If truth is an agreement between our beliefs and reality, and if reality is the thing that determines our experiences, then it is only meaningful to talk about beliefs being true if there are some sequences of possible experiences that could cause the belief to be either true or false. This is perhaps too restrictive a use of "reality", but certainly such beliefs can be meaningfully discussed.
Unfortunately, I would like to base my actions upon beliefs that do not fall into this category. Things like "the universe will continue to exist after I die" does not have any direct implications on my lifetime experiences, and thus would be considered meaningless. Fortunately, I have found a general transformation that turns such beliefs into beliefs that often have meaning. The basic idea is to instead of asking directly about my experiences to instead use Solomonoff induction to ask the question indirectly. For example, the question above becomes (roughly) "will the simplest model of my lifetime experiences have things corresponding to objects existing at times later than anything correspond to me?" This new statement could be true (as it is wit
1
In case you were exposing a core uncertainty you had - 'I want a) people to exist after me more than I want b) a MODEL that people exist after me, but my thinking incorporates b) instead of a); and that means my priorities are wrong' - and it's still troubling you, I'd like to suggest the opposite: if you have a model that predicts what you want, that's perfect! Your model (I think) takes your experiences, feeds them into a Bayesian algo, and predicts the future - what better way is there to think? I mean, I lack such computing power and honesty...but if an honest computer takes my experiences and says, 'Therefore, people exist after me,' then my best possible guess is that people exist after me, and I can improve the chance of that using my model.
0
Only propositions that constrain our sensory experience are meaningful.
If it turns out that the cosmologists are wrong and the universe begins to contract, we will have the opportunity to make contact with the civilization that the colonization starship spawns. The proposition "The starship exists" entails that the probability of the universe contracting and us making contact with the descendants of the passengers of the starship is substantial compared to the probability of the universe contracting.
Counter-example. "There exists at least one entity capable of sensory experience." What constraints on sensory experience does this statement impose? If not, do you reject it as meaningless?
1
Heh. Okay, this and dankane's similar proposition are good counterexamples.
5
Least convenient possible world - we discover the universe will definitely expand forever. Now what?
Or what about the past? If I tell you an alien living three million years ago threw either a red or a blue ball into the black hole at the center of the galaxy but destroyed all evidence as to which, is there a fact of the matter as to which color ball it was?
1
"Possible" is an important qualifier there. Since 0 and 1 are not probabilities, you are not describing a possible world.
0
The comment doesn't lose too much if we take 'definite' to mean 0.99999 instead of 1. (I would tend to write 'almost certainly' in such contexts to avoid this kind of problem.)
2
Yvain's objection fails if "definitely" means "with probability 0.99999". In that case the conditional probability P( encounter civilization | universe contracts) is well-defined.
0
Oh, I thought I retracted the grandparent. Nevermind---it does need more caveats in the expression for it to return to being meaningful.
2
I think it loses its force entirely in that case. Nisan's proposal was a counterfactual, and Yvain's counter was a possible world where that counterfactual cannot obtain. Since there is no such possible world, the objection falls flat.
2[anonymous]
If this claim is meaningful, isn't Nisan's proposal false?
0
No. Why would that be?
0
I suspect that the answer to the alien-ball case may be empirical rather than philosophical.
Suppose that there existed quantum configurations in which the alien threw in a red ball, and there existed quantum configurations in which the alien threw in a blue ball, and both of those have approximately equal causal influence on the configuration-cluster in which we are having (approximately) this conversation. In this case, we would happen to be living in a particular type of world such that there was no fact of the matter as to which color ball it was (except that e.g. it mostly wasn't green).
0
You're right, my principle doesn't work if there's something we believe with absolute certainty.
If we later find out that the alien did in fact leave some evidence, and recover that evidence, we'll have an opinion about the color of the ball.
0[anonymous]
This seems to be avoiding Yvain's question by answering a preferred one.
The position expressed so far, combined with the avoidance here would seem to give the answer 'No'.
4
What about the proposition "the universe will cease to exist when I die" (using some definition of "die" that precludes any future experiences, for example, "die for the last time")? Then the truth of this proposition does not constrain sensory input (because it only makes claims about times after which you have no sensory input), but does have behavioral ramifications if you are, for example, deciding whether or not to write a will.
-8
-9[anonymous]
2
Can you amplify? I'd thought I'd looked this up.
Photoreceptor cells produce graded potential, not action potential. It goes through a bipolar cell and a ganglion cell before finally spiking, in a rather processed form.
2
Ah, thanks!
I don't think EY has chosen the most useful way to proceed on a discussion of truth. He has started from an anecdote where the correspondence theory of truth is the most applicable, and charges ahead developing the correspondence theory.
We call some beliefs true, and some false. True and false are judgments we apply to beliefs - sorting them into two piles. I think the limited bandwidth of a binary split should already be a tip off that we're heading down the wrong path.
In practice, ideas will be more or less useful, with that usefulness varying depending on the specifics of the context of the application of those beliefs. Even taking "belief as predictive model" as given, it's not that a belief is either accurate or inaccurate, but it will be more or less accurate, and so more or less useful, as I've claimed is the general case of interest.
Going back to the instrumental versus epsitemic distinction, I want to win, and having a model that accurately predicts events is only one tool for winning among many. It's a wonderful simulation tool, but not the only thing I can do with beliefs.
If I'm going to sort beliefs into more and less useful, the first thing to do is identif...
And yet it seems to me - and I hope to you as well - that the statement "The photon suddenly blinks out of existence as soon as we can't see it, violating Conservation of Energy and behaving unlike all photons we can actually see" is false, while the statement "The photon continues to exist, heading off to nowhere" is true. And this sort of belief can have behavioral consequences!
The belief that someone is epiphenomenally a p-zombie, or belief in consubstantiality can also have behavioral consequences. Classifying some author as an "X" can, too.
If an author actually being X has no consequences apart from the professor believing that the author is "X", all consequences accrue to quoted beliefs and we have no reason to believe the unquoted form is meaningful or important. As for p-zombieness, it's not clear at this point in the sequence that this belief is meaningless rather than being false; and the negation of the statement, "people are not p-zombies", has phrasings that make no mention of zombiehood (i.e., "there is a physical explanation of consciousness") and can hence have behavioral consequences by virtue of being meaningful even if its intuitive "counterargument" has a meaningless term in it.
2
Can someone please explain to me what is bad or undesirable about the parent? I thought it made sense, even if on a topic I don't much care about. Others evidently didn't. While we are at it, what is so insightful about the grandparent? I just thought it kind of missed the point of the quoted paragraph.
1
My guess? "Behavorial consequences" is not really the touchstone of truth under the Correspondence Theory, so EY's use of the phrase when trying to persuade us of the Correspondence Theory of Truth leaves him open to criticism. EY's response is to deny any mistake.
1
My guess? People are more or less randomly downvoting me these days, for standard fear and hatred of the admin. I suppose somebody's going to say that this is an excuse not to update, but it could also be, y'know, true. It takes a pretty baroque viewpoint to think that I was talking deliberate nonsense in that paragraph, and if anyone hadn't understood what I meant, they could've just asked.
To clarify in response to your particular reply:
Generally speaking but not always, for our belief about something to have behavioral consequences, we have to believe it has consequences which our utility function can run over, meaning it's probably linked into our beliefs about the rest of the universe, which is a good sign. There's all kinds of exceptions to this for meaningless beliefs that have behavioral consequences anyway, and a very large class of exceptions is the class where somebody else is judging what you believe, like the example someone not-Carl-who-Carl-probably-talked-to recently gave me for "Consubstantiality has the consequence that if it's true and you don't believe in it, God will send you to hell", which involves just "consubstantiality" and not consubstantiality, similarly with the tests being graded (my attempt to find a non-religious conjugate of something for which the religious examples are much more obvious).
My guess? People are more or less randomly downvoting me these days, for standard fear and hatred of the admin. I suppose somebody's going to say that this is an excuse not to update, but it could also be, y'know, true.
A review of your recent comments page puts most of the comments upvoted and some of them to stellar levels---not least of which this post. This would suggest that aversion to your admin-related commenting hasn't generalized to your on topic commenting just yet. Either that or all your upvoted comments are so amazingly baddass that they overcome the hatred while the few that get net downvotes were merely outstanding and couldn't compensate.
1
Or the downvoters are fast and early, the upvoters arrive later, which is what I've observed. I'm actually a bit worried about random downvoting of other users as well.
8
Or it's just more memorable when this happens.
4
Ahh, those kind of downvotes. I get those patterns from time to time---not as many or fast as you are able to I'm sure since I'm a mere commenter. I remind myself to review my comments a day or two later so that some of the contempt for voter judgement can bleed away after I see the correction.
2
I've noticed the same thing once or twice--less often than you, and far less often than EY, but my (human, therefore lousy) memory says it's more likely for a comment of mine to go to -1 and then +1 than the reverse.
0
I think smart statistical analysis of the voting records should reveal hate-voting if it occurs, which I agree with you that it probably does.
0
Ok, I think both you and Carl read more of an implied argument into Eliezer's mention of that particular fact than I did.
1
No consequences meaning no consequences, or no consequences meaning no empirical testability? Consider replacing the vague and subjective predicate "Post Utopian" with the even more subjective "good". If a book is (believed to be) good or bad, that clearly has consequences, such as ones willingness to read it.
There are two consistent courses here: you can expand the notion of truth to include judgements of value and quality backed by handwavy on-empirical arguments; or you can keep a narrow, positivist notion of truth and abandon the use of handwaviness yourself. And you are not doing the latter because your arguments for MWI (to take just one example) are non-empirical handwaviness.
0
How do you infer "there is a physical explanation of consciousness" from "people are not p-zombies"?
The pictures are a nice touch.
Though I found it sort of unnerving to read a paragraph and then scroll down to see a cartoon version of the exact same image I had painted inside my head, several times in a row.
Two quibbles that could turn out to be more than quibbles.
The concept of truth you intend to defend isn't a correspondence theory--rather it's a deflationary theory, one in which truth has a purely metalinguistic role. It doesn't provide any account of the nature of any correspondence relationship that might exist between beliefs and reality. A correspondence theory, properly termed, uses a strong notion of reference to provide a philosophical account of how language ties to reality.
You write:
Some pundits have panicked over the point that any judgment of truth - any comparison of belief to reality - takes place inside some particular person's mind; and indeed seems to just compare someone else's belief to your belief.
I'm inclined to think this is a straw man. (And if they're mere "pundits" and not philosophers why the concern with their silly opinion?) I think you should cite to the most respectable of these pundits or reconsider whether any pundits worth speaking of said this. The notion that reality--not just belief--determines experiments, might be useful to mention, but it doesn't answer any known argument, whether by philosopher or pundit.
The quantum-field-theory-and-atoms thing seems to be not very relevant, or at least not well-stated. I mean, why the focus on atoms in the first place? To someone who doesn't already know, it sounds like you're just saying "Yes, elementary particles are smaller than atoms!" or more generally "Yes, atoms are not fundamental!"; it's tempting to instead say "OK, so instead of taking a possible state of configurations of atoms, take a possible state of whatever is fundamental."
I'm guessing the problem you're getting at is that is that when you actually try to do this you encounter the problem that you quickly find that you're talking about not the state of the universe but the state of a whole notional multiverse, and you're not talking about one present state of it but its entire evolution over time as one big block, which makes our original this-universe-focused, present-focused notion a little harder to make sense of -- or if not this particular problem then something similar -- but it sounds like you're just making a stupid verbal trick.
3
I agree - atoms and so forth are what our universe happens to consist of. But I can't see why that's relevant to the question of what truth is at all - I'd say that the definition of truth and how to determine it are not a function of the physics of the universe one happens to inhabit. Adding physics into the mix tends therefore to distract from the main thrust of the argument - making me think about two complex things instead of just one.
There's no reason for your brain not to update if politics aren't involved.
I don't agree nor like this singling-out of politics as the only thing in which people don't update. People fail to update in many fields, they'll fail to update in love, in religion, in drug risks, in ... there is almost no domain of life in which people don't fail to update at times, rationalizing instead of updating.
In addition to what pleeppleep said, I think there is a bit of illusion of transparency here.
As I've said elsewhere, what Eliezer clearly intends with the label "political" is not partisan electioneering to decide whether the community organizer or the business executive is the next President of the United States. Instead, he means something closer to what Paul Graham means when he talks about keeping one's identity small.
Among humans at least, "Personal identity is the mindkiller."
4
This is evidently confusing readers, since over here someone thought it was about "social manipulation, status, and signaling".
1
I must confess that I don't seem any substantial disagreement between my articulation of EY's views and pleeppleep's articulation.
There are certain kinds of inter-personal conflicts that effect a person's mental processes such that the person does not update on the evidence the way rationality says they should. These inter-personal conflicts can profitably labelled with the word "politics." But these inter-personal conflicts include more than those I've labeled "partisan electioneering."
Whether "status-challenge" or "threat-to-personal-identity" is the more accurate description of the causal factors leading to this phenomena is not particularly important to understanding what EY meant when he said "Politics is the mindkiller."
0
Still, there may be a better word than “politics” for him to use.
2
He didn't say "politics" was special. He seemed to be pointing out that updating is called for in circumstances other than the example. "Politics" is used to represent all other issues, and it was relevant because a common criticism of truth is that it is an illusion used to gain a political advantage.
Highly Advanced Epistemology 101 for Beginners
The joke flew right over my head and I found myself typing "Redundant wording. Advanced Epistemology for Beginners sounds better."
Oh come on, yeah the gender-imbalance of the original images was bad, but ugliness is also bad and the new stick figures are ugly...
4
Agreed. The previous illustrations were pretty awesome, and this post has lost a lot for it.
2
Agreed. The stick figures do not mesh well with the colourful cartoony backgrounds that make the images visually appealing. They feel out of place, and I found it harder to tell when I was supposed to consider one stick figure distinct from another one without actively looking for it (I also have this problem with xkcd).
Strong vote for return to the original style diagrams, with the gender imbalance fixed.
2
[looks back at the top-level post] Yes, they are. Especially the professor in the last picture -- it reminds me of Jack Skellington from A Nightmare Before Christmas. Using thinner lines à la xkcd would be better, IMO.
0
I didn't see the old stick figures, but I think the ones that are there now are fine.
2
Good quote, but what about the reality that I believe something? ;) The fact that beliefs themselves are real things complicates this slightly.
0
It's possible to stop believing that you believe something while continuing to believe it. It's rare, and you won't notice you did so, but it can happen.
5
I could figure some cases where would find it natural to say that one proposition is more accurate then another, but not to say that it is more true. For example, saying that my home has 1000 ft.², as opposed to saying that has 978.25 ft.² Or saying that it is the morning, as opposed to saying that it is 8:30 AM.
0
In that context it would refer to narrowness, but it would refer to proximity to truth in a different context, so I think its one of those cases where one word is used twice in place of a second word. I don't think narrowness would be confused with truth, so I think my first definition is the more relevant.
2
Perhaps this: "accuracy" is a quantitative measue when "truth" is only qualitative/categorical.
-2
"Truth" and "accuracy" are just words, and there is no inherent difference between them.
That said, if you wanted to assign useful meaning to the two, you could use truth as a noun to describe the condition of belief matching reality, and accuracy as an adjective to refer to the place of a condition on a scale of proximity between belief and reality.
Or, you could use them the other way around.
Or, you could use both words as nouns in one context, and adjectives in another. This is usually the case, with accuracy more likely to be used as an adjective as it implies lack of confidence to some degree.
0
That wasn't helpful.
0
I answered your question. You should rephrase it if you want to learn something else.
-1
And what CronoDAS really meant was
"What is the difference between truth and accuracy?", I suppose?
As a graduate philosophy student, who went to liberal arts schools, and studied mostly continental philosophy with lots of influence from post-modernism, we can infer from the comments and articles on this site that I must be a complete idiot that spouts meaningless jargon and calls it rational discussion. Thanks for the warm welcome ;) Let us hope I can be another example for which we can dismiss entire fields and intellectuals as being unfit for "true" rationality. /friendly-jest.
Now my understanding may be limited, having actually studied pos...
6
Please do. (But . . . with paragraphs?)
0
I proffer the following quotes rather than an entire article (I think the major problem with post-modernism isn't irrationality, but verbosity. JUST LOOK AT YOURSELF):
-2
Ya, I can see that criticism. Here's a shorter version for you: arguing against post-modernism by arguing against the use of a different term (post-colonial, or even worse the made-up post-utopian) is a complete straw-man and fallacious argumentation. It also makes the OP and commenters look exceptionally naive when the thing they argue against (post-modernism) would actually agree with their point (critiquing literary genres), and preempted them in making it (thus the discussion of deconstruction above).
Also, thanks for the quotes :) And remember, being overly verbose is a critique of communication, not of the rationality of a position or method. SELF-EXAMINATION & MODIFICATION COMPLETE
Didn't you say you were working on a sequence on open problems in friendly AI? And how could this possibly be higher priority than that sequence?
Two minor grammatical corrections:
A space is missing between "itself" and "is " in "The marble itselfis a small simple", and between "experimental" and "results" in "only reality gets to determine my experimentalresults".
This post starts out by saying that we know there is such a thing as truth, because there is something that determines our experimental outcomes, aside from our experimental predictions. But by the end of the post, you're talking about truth as correspondence to an arrangement of atoms in the universe. I'm not sure how you got from there to here.
7
We know there's such a thing as reality due to the reasons you mention, not truth - that's just a relation between reality and our beliefs.
"Arrangements of atoms" play a role in the idea that not all "syntactically correct" beliefs actually are meaningful and the last koan asks us to provide some rule to achieve this meaningfulness for all constructible beliefs (in an AI).
At least that's my understanding...
Great post! If this is the beginning of trend to make Less Wrong posts more accessible to a general audience, then I'm definitely a fan. There's a lot of people I'd love to share posts with who give up when they see a wall of text.
There are two key things here I think can be improved. I think they were probably skipped over for mostly narrative purposes and can be fixed with brief mentions or slight rephrasings:
...You won't get a direct collision between belief and reality - or between someone else's beliefs and reality - by sitting in your living-room w
hello. it is not a mayor problem, but i just wanted to put it out there: i would love it if there were some bibliographical references which we could look into :)
best regards, i just found Less Wrong and it's amazing
edit1: i mean references as footnotes in every entry, although that may substract from the reading experience?
4
The Bibliography of Eliezer’s book, Rationality: From AI to Zombies, may be of interest to you.
1
thank. you. so. much.
i was wondering specifically about bibliography regarding the following:
" Since my expectations sometimes conflict with my subsequent experiences, I need different names for the thingies that determine my experimental predictions and the thingy that determines my experimental results. I call the former thingies 'beliefs', and the latter thingy 'reality'".
I suspect the most relevant reference towards it would be Feldman, Richard. “Naturalized Epistemology.” In The Stanford Encyclopedia of Philosophy, Summer 2012, edited by Edward N. Zalta.
Correct me if i'm wrong, also, if you know of a another reference it would be awesome.
2
I confess I am not entirely clear on what it is that you’re looking for.
The quoted comment does not seem to be the sort of thing that one would cite a source for… or am I misunderstanding your question?
1
It may not be the sort of thing one would cite a source for, at least authoritatively .
Sorry, maybe I should clarify that I'm a law student and I'm used to reading texts with tons of footnotes and references per page, which serve to refer where to find extensive information about a particular idea, and also sometimes for making somewhat stupid ad verecundiam arguments.
I was just wondering if Yudkowsky came up with the idea behind the parragraph I quoted entirelly on his own (which is TOTALLY fine) or if he had some sources that served as inspiration.
I understand that the truth-value of what he says is independent from whether he quotes sources or not, I just wanted to know if there are materials that expand specifically about the main idea behind what I quoted.
Also, thank you for the patience.
5
Ah, I see.
As far as whether Eliezer came up with the idea on his own—as with most (though not all) of his ideas, the answer, as I understand it, is “sort of yes, sort of no”. To expand a bit: much of what Eliezer says is one or both of: (a) prefigured in the writings of other philosophers / mathematicians / etc., (b) directly inspired by some combination of things he’d read. However, the presentation, the focus, the emphasis, etc., are often novel, and the specifics may be a synthesis of multiple extant sources, etc.
In this particular case, I do not recall offhand whether Eliezer ever mentioned a specific inspiration. But as far as there being other sources for this idea—they certainly exist. You may want to start with the SEP page on the “correspondence theory of truth”, and go from there, following references and so on. (In general, the SEP will serve well as your first port of call for finding detailed accounts of, and references about, ideas in philosophy.)
1
Thank you so much!! This is what I didn't know I was looking for!
Beliefs should pay rent, check. Arguments about truth are not just a matter of asserting privilege, check. And yet... when we do have floating beliefs, then our arguments about truth are largely a matter of asserting privilege. I missed that connection at first.
Why did you reply directly to the top-level post rather than to where the quotation was taken from?
Here's my map of my map with respect to the concept of truth.
Level Zero: I don't know. I wouldn't even be investigating these concepts about truth unless on some level I had some form of doubt about them. The only reason I think I know anything is because I assume it's possible for me to know anything. Maybe all of my priors are horribly messed up with respect to whatever else they potentially should be. Maybe my entire brain is horribly broken and all of my intuitive notions about reality and probability and logic and consistency are meaningless. There's ...
Highly Advanced Epistemology 101 for Beginners
What does it tell about me that I mentally weighed "Highly Advanced" on a scale pan and "101" and "for Beginners" on the other pan?
I would have inverted the colours in the “All possible worlds” diagram (but with a black border around it) -- light-on-black reminds me of stars, and thence of the spatially-infinite-universe-including-pretty-much-anything idea, which is not terribly relevant here, whereas a white ellipse with a black border reminds me of a classical textbook Euler-V...
0
Your beliefs about the functionality of a "medicine," and the parts of your physiology that make the placebo effect work, are both part of reality. Your beliefs can, in a few (really annoying!) cases, affect their own truth or falsity, but whenever this happens there's a causal chain leading from the neural structure in your head to the part of reality in question that's every bit as valid as the causal chain in the shoelace example.
0
I think that if you're human, these cases are way more common than ISTM certain people realize. So in such discussions I'd always make clear if I'm talking about actual humans, about future AIs, or about idealized Cartesian agents whose cognitive algorithms cannot affect the world in any way, shape or form until they act on them.
0
Can I have a couple examples other than placebo affect? Preferably only one of which is in the class "confidence that something will work makes you better at it"? Partly because it's useful to ask for examples, partly because it sounds useful to know about situations like this.
0
Actually, pretty much all I had in mind was in the class "confidence that something will work makes you better at it" -- but looking up “Self-fulfilling prophecy” on Wikipedia reminded me of the Observer-expectancy effect (incl. the Clever Hans effect and similar). Some of Bostrom's information hazards also are relevant.
0
Ehn, the truth value depends on context too. "That girl over there heard what this guy just said" is true if that girl over there heard what this guy just said, false if she didn't, and meaningless if there's no girl or no guy or he didn't say anything.
Common knowledge, in general?
Beliefs are a strict subset of reality.
0
I was thinking more about stuff like, “but reality does also include my map, so a map of reality ought to include a map of itself” (which, as you mentioned, is related to my point about placebo-like effects).
Suppose I have two different non-meaningful statements, A and B. Is it possible to tell them apart? On what basis? On what basis could we recognize non-meaningful statements as tokens of language at all?
Connotation. The statement has no well-defined denotation, but people say it to imply other, meaningful things. Islam is a religion of peace!
2[anonymous]
Good answer. So, if I've understood you, you're saying that we can recognize meaningless statements as items of language (and as distinct from one another even) because they consist of words that are elsewhere and in different contexts meaningful.
So for example I may have a function "...is green." where we can fill this in with true objects "the tree", false objects "the sky" and objects with render the resulting sentence meaningless, like "three". The function can be meaningfully filled out, and 'three' can be the objet of a meaningful sentence ('three is greater than two') but in this connection the resulting sentence is meaningless.
Does that sound right to you?
0
OTOH, there is no reason to go along with the idea that denotion (or empirical consequence) is essential to meaning. You could instead use you realisation that you actually can tell the difference between untestable statements to conclude that they are in fact meaningful, whatever warmed-over Logical Positivism may say.
0
It's not useful to know they are meaningful if you don't know the meaning.
0
You do know the meaning. Knowing the meaning is what tells you there is no denotation. You know there is no King of France because you know what "King" and "France" mean.
0
I wouldn't agree with this. Knowing whether or not something is meaningful is potentially quite a lot of information.
3
Why would you want to?
0
See this.
2
Not sure how this is relevant, feel free to elaborate.
-2
What an odd thing to say. I can tell the difference between untestable sentences, and that's all I need to refute the LP verification principle. Stipulating a defintion of "meaning" that goes beyond linguistic tractability doens't solve anything , and stipulating that people shouldn't want to understand sentences about invisible gorillas doens't either.
4
Seems like we are not on the same page re the definition of meaningful. I expect "invisible gorillas" to be a perfectly meaningful term in some contexts.
0
I don't follow that, because it is not clear whether you are using the vanilla, linguistic notion of "meaning" or the stipulated LPish version,
0
I am not a philosopher and not a linguist, to me meaning of a word or a sentence is the information that can be extracted from it by the recipient, which can be a person or a group of people, or a computer, maybe even an AI. Thus it is not something absolute. I suppose it is closest to an internal interpretation#Meaning_as_internal_interpretation). What is your definition?
0
I am specifically trying not to put forward an idiosyncratic definition.
0
How are you encoding the non-meaningful statements? If they're encoded as characters in a string, then yes we can tell them apart (e.g. "fiurgrel" !== "dkaldjas").
Why do you want to tell them apart?
So... could this style of writing, with koans and pictures, be applied to transforming the majority of sequences into an even greater didactic tool?
Besides the obvious problems, I'm not sure how this would stand with Eliezer - they are, after all, his masterpiece.
6
Really, more like his student work. It was "Blog every day so I will have actually written something" not "Blog because that is the ultimate expression of my ideas".
7
Yep. The main problem would be that I'd been writing for year and years before then, and, alas for our unfair universe, also have a certain amount of unearned talent; finding somebody who can pick up the Sequences and improve them without making them worse, despite their obvious flaws as they stand, is an extremely nontrivial hiring problem.
-2
Not to mention that any candidate up to the task likely has more lucrative alternatives...
Reply: The abstract concept of 'truth' - the general idea of a map-territory correspondence - is required to express ideas such as: ...
Is this true? Maybe there's a formal reason why, but it seems we can informally represent such ideas without the abstract idea of truth. For example, if we grant quantification over propositions,
Generalized across possible maps and possible cities, if your map of a city is accurate, navigating according to that map is more likely to get you to the airport on time.
becomes
- Generalized across possible maps and possib
6
If you can generalize over the correspondence between p and the quoted version of p, you have generalized over a correspondence schema between territory and map, ergo, invoked the idea of truth, that is, something mathematically isomorphic to in-general Tarskian truth, whether or not you named it.
4
Well, yeah, we can taboo 'truth'. You are still using the titular "useful idea" though by quantifying over propositions and making this correspondence. The idea that there are these things that are propositions and that they can appear both in quotation marks and also appear unquoted, directly in our map, is a useful piece of understanding to have.
Koan: If we were dealing with an Artificial Intelligence that never had to argue politics with anyone, would it ever need a word or a concept for 'truth'?
I'm not sure what this has to do with politics? The lead-up discusses "an Artificial Intelligence, which was carrying out its work in isolation" — the relevant part seems to be that it doesn't interact with other agents at all, not that it doesn't do politics specifically. Even without politics, other agents can still be mistaken, biased, misinformed, or deceitful; and one use of the concept of "truth" has to do with predicting the accuracy of others' statements and those people's intentions in making them.
2
I think politics is used to refer to social manipulation, status, and signaling here. The example is used to designate an agent that has no concern for asserting social privilege over others.
0[anonymous]
In addition to what pleeppleep said, I think there is a bit of illusion of transparency here.
As I've said elsewhere, what Eliezer clearly intends with the label "political" is not partisan electioneering to decide whether the community organizer or the business executive is the next President of the United States. Instead, he means something closer to what Paul Graham means when he talks about keeping one's identity small.
Among humans at least, "Personal identity is the mindkiller."
for a part of your brain's world-model to be meaningful doesn't require that you can explain it in words.
so, hmm, what do we do with this part? how do we model/measure it? also, how much meaning escapes words at an individual/group level?
consciously note the difference between your reply and the post's reply, including any extra details present or missing, without trying to minimize or maximize the difference.
this is a great prompt & I'm curious if you have some guidance on how one can do that better than one currently does it.
If the above is true, aren't the postmodernists right? Isn't all this talk of 'truth' just an attempt to assert the privilege of your own beliefs over others, when there's nothing that can actually compare a belief to reality itself, outside of anyone's head?
No, we are talking about personal epistemology. That is, if we cannot compare a belief to reality, you cannot also compare it to some other persons beliefs (there is reality at least in between). We want truth to be a way of privledging some of our beliefs over other beliefs, in a way so that we can fu...
Response to the First Meditation
Even if truth judgments can only be made by comparing maps — even if we can never assess the territory directly — there is still a question of how the territory is.
Furthermore, there is value in distinguishing our model/expectations of the world, from our experiences within it.
This leads to two naive notions of truth:
- Accurate descriptions of the territory are true.
- Expectations that match experience are true.
1
Response to the Second Meditation
For an AI that had no need to communicate with other agents, then the idea of truth serves as a succinct term for the map-territory/belief-reality correspondence.
It allows the AI to be more economical/efficient in how it stores information about its maps.
That's some value.
Saying that a proposition is true, is saying that it's an accurate description of the territory.
Tarski's Litany: "The sentence 'X' is true iff X."
The territory may be physical reality ("'the sky is blue' is true"), a formal system ("'2 + 2 = 4' is true"), other maps, etc.
"Since my expectations sometimes conflict with my subsequent experiences, I need different names for the thingies that determine my experimental predictions and the thingy that determines my experimental results. I call the former thingies 'beliefs', and the latter thingy 'reality'."
I think this is a fine response to Mr. Carrico, but not to the post-modernists. They can still fall back to something like "Why are you drawing a line between 'predictions' and 'results'? Both are simply things in your head, and since you can't directly observe reality, your 'r...
Fine, Eliezer, as someone who would really like to think/believe that there's Ultimate Truth (not based in perception) to be found, I'll bite.
I don't think you are steelmanning post-modernists in your post. Suppose I am a member of a cult X -- we believe that we can leap off of Everest and fly/not die. You and I watch my fellow cult-member jump off a cliff. You see him smash himself dead. I am so deluded ("deluded") that all I see is my friend soaring in the sky. You, within your system, evaluate me as crazy. I might think the same of you.
You mig...
1
I sort of get the point. I remember once reading here that the reason it is a decent choice to use certain axioms also used in rationality and science is that those axioms have a pretty decent track record of helping to find out truth. A track record better than say...philosophy?
1
How do you know? Science can make accurate predictions, and advise courses of action that work practically...but both of those would still be true inside the Matrix. If you think that truth is correspondence ,as rationalists are supposed to, then there is no way of proving that science is finding the truth, because there is no separate criterion that tells you correspondence has been achieved.
Philosophy doesn't have the option of passing off one kind of truth for another...someone would notice.
1
Why do you assume that we are inside the Matrix?
There is a criterion that tells you when correspondence has likely been achieved: Serialized experimental testing. Nothings is ever ABSOLUTELY EVER TRULY PROVEN, it's just that if you have a belief that can accurately precise future events (experiments), then that is a strong indicator that on some level you have knowledge about the true shape of reality.
1
I don't assume that we are inside the matrix as a matter of fact. I note that if we were, hypothetically, science would work just as well at making predictions, whilst failing completely at identifying the nature of reality. That's how I am arguing that prediction and correspondence are not identical.
That's a cached though for many people. The question is how does prediction lead to corresponence?
Maybe not, but that's not the problem. If you could make 100% accurate predictions inside the matrix, you would still have the problem outlined above.
1
due to the nature of the matrix-issue, it seems that in such case we wouldn't be able to tell that we are in the matrix. at least until that which enables the characters to tell that they are in the matrix happens to you.
however, our succesful predictions still would be able to tell us something true: that inside the matrix, physical attributes of the simulation work a certain way.
I think that succesful prediction leads to correspondence because it signals that the way you think the world is, is the way in which the world actually is. Of course, one must critically analyze every concrete case, since it's easy to misinterpret data.
1
Except that its not real physics.
How?
1
I admit my ignorance of physics. Still, the point stands: even though we wouldn't know that we were inside the Matrix, we would know how a part of it works: the "physics simulator", even though we have a "wrong" label for it, "reality" instead of "matrix simulation".
How? Interesting. How what? How it signals? You have concepts that represent how you think things are, inside your mind you imagine some way in which they would interact given the characteristics you think they have, and realize what you would (truly) have to perceive in order to confirm that interaction.
If you experiment and find out, after an honest analysis, that indeed that event was perceived, it would mean that the characteristics that you imagined the things have are indeed posesed by the things, if not they wouldn't interacted like you imagined. All of this in the case you know everything there is no know about something. One should never claim to have absolute truth, because if you are wrong you won't be able to be corrected. But of course, one can perfectly say that they have very strong reasons to believe something, because there is a history of evidence backing up that the world would work a certain way and no particular reason to believe that, for some reason, you what you believe is false and the evidence backing your false beliefs are invalid for some ??? reason. Obviously, if there is a certain anomaly that doesn't fit the model of how the world works, by all means it should be investigated. Of course, we are always discovering new information but there is a core body ok knowledge with a lot of evidence behind it.
After writing this, i think that right now i don't have the skills to put what you want to hear into words.
-1
If this wasn't clear: responses would be much more helpful than up/down votes.
2[anonymous]
I downvoted your comment because it was unclear to me what your point was. It seems to me that it lacks a single, precise focus.
1
I have the same problem with the OP?
-2
The downvotes and no reply are a pretty good example of what's wrong with less wrong. Someone who is genuinely confused should not be shooed away then insulted when they ask again.
First of all remember to do and be what's best. If this doubt is engendering good attitudes in you, why not keep it? The rest of this is premised on it not helping or being unhelpful.
External reality is much more likely than being part of a simulation which adjusts itself to your beliefs because a simulation which adjusts itself to your beliefs is way, way more complicated. It requires more assumptions than a single level reality. If there's a programmer of your reality, that programmer has a reality too, which needs to be explained in the same way a single level one should as does their ability to program such a lifelike entity and all sorts of other things.
More fundamentally though, this is just the reality you live in, whatever its position in a potential reality chain.
If we are being simulated, trying to metagame potential matrix lords' dispositions/ ask for favours/look for loopholes/care less about its contents is only a bug of human cognition. If this is a simulation, it is inhabited by at least me, and almost certainly many other people, and there's real consequences for all of us. If you don't earn your simulation rent you'll get kicked out of your simulation place. Qualify everything with "potentially simulated-" and it changes nothing. "Real" just isn't a useful (and so, important) distinction to make in first person reguarding simulations.
and/or you could short circuit any debilitating doubt using fighting games or sports (or engaging in other similiar activities) which illustrate the potential importance of leaning all in towards the evidence without worrying about the nature of things, and are a good way to train that habit.
Also, in this potentially simulated world, social pressure is a real thing. The more infallible and sensitive you make your thinking (or allow
A criticism - somewhat harsh but hopefully constructive.
As you know, lots of people have written on the subjects of truth and meaning (aside from Tarski). It seems, however, that you don't accord them much importance (no references, failure to consider alternate points of view, apparent lack of awareness of the significance of the matter of what the bearer of truth (sentence, proposition, 'neurally embodied belief') properly is, etc.). I put it to you this is a manifestation of irrationality: you have a known means at your disposal to learn reliably about...
6
Give me an example of a specific thing relevant to constructing an AI which I should have referenced, plus the role it plays in a (self-modifying) AI. Keep in mind that I only care about constructing self-modifying AIs and not about "what is the bearer of truth".
I've read works-not-referenced on "meaning", they just don't seem relevant to anything I care about. Though obviously there's quite a lot of standard work on mathematical proof that I care about (some small amount of which I've referenced).
1
1) I don't see that this really engages the criticism. I take it you reject that the subjects of truth and reference are important to you. On this, two thoughts:
a) This doesn't affect the point about the reliability of blogging versus research. The significance of the irrationality maybe, but the point remains. You may hold that the value to you of the creative process of explicating your own thoughts is sufficiently high that it trumps the value of coming to optimally informed beliefs - that the cost-benefit analysis favours blogging. I am sceptical of this, but would be interested to hear the case.
b) It seems just false that you don't care about these subjects. You've written repeatedly on them, and seem to be aiming for an internally coherent epistemology and semantics.
2) My claim was that your lack of references is evidence that you don't accord importance to experts on truth and meaning, not that there are specific things you should be referencing. That said, if your claim is ultimately just the observation that truth is useful as a device for so-called semantic ascent, you might mention Quine (see the relevant section of Word and Object or the discussion in Pursuit of Truth) or the opening pages of Paul Horwich's book Truth, to give just two examples.
3) My own view is that AI should have nothing to do with truth, meaning, belief or rationality - that AI theory should be elaborated entirely in terms of pattern matching and generation, and that philosophy (and likewise decision theory) should be close to irrelevant to it. You seem to think you need to do some philosophy (else why these posts?), but not too much (you don't have to decide whether the sorts of things properly called 'true' are sentences, abstract propositions or neural states, or all or none of the above). Where the line lies and why is not clear to me.
I'm saying, "Show me something in particular that I should've looked at, and explain why it matters; I do not respond to non-specific claims that I should've paid more homage to whatever."
-2
As far as I can see, your point is something like:
"Your reasoning implies I should read some specific thing; there is no such thing; therefore your reasoning is mistaken." (or, "unless you can produce such a thing...")
Is this right? In any case, I don't see that the conditional is correct. I can only give examples of works which would help. Here are three more. Your second part seeks (as I understand it) a theory of meaning which would imply that your ' Elaine is a post-utopian' is meaningless, but that 'The photon continues to exist...' is both meaningful and true. I get the impression you think that an adequate answer could be articulated in a few paragraphs. To get a sense of some of the challenges you might face -ie, of what the project of contriving a theory of meaning entails- consider looking at Stephen Schiffer's excellent Remnants of Meaning and The Things we Mean or Scott Soames's What is Meaning? .
4
I think it's more like
"Your reasoning implies I should have read some specific idea, but so far you haven't given me any such idea and why it should matter, only general references to books and authors without pointing to any specific idea in them"
Part of the talking-past-each-other may come from the fact that by "thing", Eliezer seems to mean "specific concept", and you seem to mean "book".
There also seems to be some disagreement as to what warrants references - for Eliezer it seems to be "I got idea X from Y", for you it's closer to "Y also has idea X".
0[anonymous]
"If there is such a thing and you know it, you should be able to describe it at least partially to a highly informed listener who is already familiar with the field. Your failure to describe this thing causes me to think that you might be trying to look impressive by listing a lot of books which, for all I know at this point, you haven't even read."
0
Your comment carries the assumption that studying the work of experts makes you better at understanding epistemology, and I'm not sure why you think that. Much of philosophy has a poor understanding of epistemology, in my mind. Can you explain why you think reading the work of experts is important for having worthwhile thoughts on epistemology?
5
This seems to me a reasonable question (at least partly - see below). To be clear, I said that reading the work of experts is more likely to produce a good understanding than merely writing-up one's own thoughts. My answer:
For any given field, reading the thoughts of experts -ie, smart people who have devoted substantial time and effort to thinking and collaborating in the field- is more likely to result in a good understanding of the field's issues than furrowing one's brow and typing away in relative isolation. I take this to be common sense, but please say if you need some substantiation. The conclusion about philosophy follows by universal instantiation.
"Ah", I hear you say, "but philosophy does not fit this pattern, because the people who do it aren't smart. They're all at best of mediocre intelligence." (is there another explanation of the poor understanding you refer to?). From what I've seen on LW, this position will be inferred to from a bad experience or two with philosophy profs , or perhaps on the grounds that no smart person would elect to study such a diseased subject.
Two rejoinders:
i) Suppose it were true that only second rate thinkers do philosophy. It would be still the case that with a large number of people discussing the issues over many years, there'd be a good chance something worth knowing -if there's anything to know- would emerge. It wouldn't be obvious that the rational course is to ignore it, if interested in the issues.
ii) It's obviously false (hence the 'partly' above). Just try reading the work of Timothy Williamson or David Lewis or Crispin Wright or W.V.O. Quine or Hilary Putnam or Donald Davidson or George Boolos or any of a huge number of other writers, and then making a rational case that the leading thinkers of philosophy are second-rate intellects. I think this is sufficiently obvious that the failure to see it suggests not merely oversight but bias.
Philosophical progress may tend to take the form just of increasingly
5
There's no fool like an intelligent fool. You have to be really smart to be as stupid as a philosopher.
Even in antiquity it was remarked that "no statement is too absurd for some philosophers to make" (Cicero).
If ever one needed a demonstration that intelligence is not usefully thought of as a one-dimensional attribute, this is it.
When I hear the word "nuanced", I reach for my sledgehammer.
2
Quoting this.
4
Reading the work of experts also puts you in a position to communicate complex ideas in a way others can understand.
1
I think philosophers include some smart people, and they produced some excellent work (some of which might still help us today). I also think philosophy is not a natural class. You would never lump the members of this category together without specific social factors pushing them together. Studying "philosophy" seems unlikely to produce any good results unless you know what to look for.
I have little confidence in your recommendations, because your sole concrete example to date of a philosophical question seems ludicrous. What would change if a neurally embodied belief rather than a sentence (or vice versa) were the "bearer of meaning"? And as a separate question, why should we care?
2
The issue is whether a sentence's meaning is just its truth conditions, or whether it expresses some kind of independent thought or proposition, and this abstract object has truth conditions. These are two quite different approaches to doing semantics.
Why should you care? Personally, I don't see this problem has anything to do with the problem of figuring out how a brain acquires the patterns of connections needed to create the movements and sounds it does given the stimuli it receives. To me it's an interesting but independent problem, and the idea of 'neurally embodied beliefs' is worthless. Some people (with whom I disagree but whom I nevertheless respect) think the problems are related, in which case there's an extra reason to care, and what exactly a neurally embodied belief is, will vary. If you don't care, that's your business.
2
This has done very little to convince me that I should care (and I probably care more about academic Philosophy than most here).
1
Thanks for pointing this out. I tend to conflate the two, and it's worth keeping the distinction in mind.
0
You mention that an AI might need a cross-domain notion of truth, or might realise that truth applies accross domains. Michael Lynch's functionalist thbeory of truth, mentioned elsewhere on this page, is such a theory.
I don't understand the part about post-utopianism being meaningless. If people agree on what the term means, and they can read a book and detect (or not) colonial alienation, and thus have a test for post-utopianism, and different people will reach the same conclusions about any given book, then how exactly is the term meaningless?
6
I think "postmodernism," "colonial alienation," and "post-utopianism" are all meant to be blanks, which we're supposed to fill in with whatever meaningless term seems appropriate.
But I share your uneasiness about using these terms. First, I don't know enough about postmodernism to judge whether it's a field filled with empty phrases. (Yudkowsky seems to take the Sokal affair as a case-closed demonstration of the vacuousness of postmodernism. However, it is less impressive than it may seem at first. The way the scandal is presented by some"science-types"--as an "emperor's new clothes" story, with pretentious, obfuscationist academics in the role of the court sycophants--does not hold up well after reading the Wikipedia article. The editors of Social Text failed to adhere to appropriate standards of rigor, but it's not like they took one look at Sokal's manuscript and were floored by its pseudo-brilliance.)
Second, I suspect there aren't any clear-cut examples of meaningless claims out there that actually have any currency.(I only suspect this; I'm not certain. Some things seem meaningless to me; however, that could be just because I'm an outsider.)
Counterexamples?
2
By hypothesis, none of those things are true. If those things happen to be true for "post-utopianism" in the real world, substitute a different word that people use inconsistently and doesn't refer to anything useful.
0
But, from the article:
Seems like what I was saying...
Similarly, to say of your own beliefs, that the belief is 'true', just means you're comparing your map of your map, to your map of the territory
I assume this is meant in the spirit of "it's as if you are", not "your brain is computing in these terms". When I anticipate being surprised, I'm not consciously constructing any "my map of my map of ..." concepts. Whether my brain is constructing them under the covers remains to be demonstrated.
Thus, after the photon goes past a certain point, there are no experimental consequences whatsoever, ever, to the statement "The photon continues to exist, rather than blinking out of existence."
One shouldn't form theories about a particular photon. The statement "photons in general continue to exist after crossing the cosmological horizon" and "photons in general blink out of existence when they cross the cosmological horizon" have distinct testable consequences, if you have a little freedom of motion.
Since my expectations sometimes conflict with my subsequent experiences, I need different names for the thingies that determine my experimental predictions and the thingy that determines my experimental results. I call the former thingies 'beliefs', and the latter thingy 'reality'.
I think it's apt but ironic that you find a definition of "truth" by comparing beliefs and reality. Beliefs are something that human beings, and maybe some animals have. Reality is vast in comparison, and generally not very animal-centric. Yet every one of these d...
1
Truth is more about how you get to know reality than it is about reality. For instance, it is easy to conceive of a possibility where everything a person knows about something points to it being true, even if it later turns out to be false. Even if you do everything right, there's no cosmic guarantee that you have found truth, and therefore cut straight through to reality.
But it is still a very important concept. Consider: someone you love is in the room with you, and all the evidence available to you points to a bear trying to get into the room. You would be ill-advised to second-guess your belief when there's impending danger.
Not exactly. White isn't a fundamental concept like mass is. Brain perception of color is an extremely relative and sticky issue. When I go outside at night and look at snow, I'd swear up and down that the stuff is blue.
0
If people weren't around, then "snow is white" would still be a true sentence, but it wouldn't be physically embodied anywhere (in quoted form). If we want to depict the quoted sentence, the easiest way to do that is to depict its physical embodiment.
People usually are not mistaken about what they themselves believe - though there are certain exceptions to this rule - yet nonetheless, the map of the map is usually accurate, i.e., people are usually right about the question of what they believe:
I'm not at all sure about this part - although I don't think it matters much to your overall case. I think one of our senses is a very much simplified representation of our own internal thought state. It's only just about good enough for us to make a chain of thought - taking the substance of a finished though...
The "All possible worlds" picture doesn't include the case of a marble in both the basket and the box.
9
This sentence is hilarious out of context.
8
Also presumably a true one, assuming he aims the 'was' correctly.
0
And the 'marble'. I would assume the word came about long after we started making things that could be described by it - tracking down the 'first' one might be really tricky. It could be as bad as trying to find the time when there was only one human.
2
Possibly harder, given the possibility that objects more closely resembling an archetypal marble than the first marbles actively created probably existed elsewhere by chance. In fact, given the simplicity of the item and the material, marble-like objects probably existed a long time ago in a galaxy far far away. Humans on the other hand are sufficiently complex, arbitrary and anthropically selected that we can with reasonable confidence narrow 'first human' down one of the direct ancestors of the surviving humans (or maybe the cousin of one of those ancestors if we are being cautious).
ie. In addition to the 'where do you draw the line' question you also have the 'if a marble-equivalent-object falls in forest and there is nobody there to hear it or ascribe it it purpose is it really a marble'? Then, unless you decide that spheres made out of marble aren't 'marbles' unless proximate intelligent agents intend them to be you are left with an extremely complex and abstract application of theoretical physics, cosmology, geology and statistics.
I would probably start making an estimate by looking at when second generation planets first formed.
0
I think this is gracefully resolved by adding the conditional that the object must have come into shape by causal intervention of a human mind which predicted creation of this physical form.
That just might be too many conditions and too complex a proposition, though.
0
It has to be resolved one way or the other. They are both coherent questions, they just shouldn't be confused.
2
True. I hadn't interpreted that as the point you were making, but in retrospect your comment makes sense if you had already thought of this.
0
To be precise, it is a presumably-true sentence about a presumably-true belief.
4
I would like to thank you for bringing my attention to that sentence without any context.
6
Technically, if you put the basket in the box (or vice versa), you could still have a marble in both the basket and the box with only one marble in the universe.
9
You're technically correct. THE BEST KIND OF CORRECT.
0
This is definitely not the only method to achieve this, if you take "all possible worlds" literally and start playing with laws of physics.
Since my expectations sometimes conflict with my subsequent experiences, I need different names for the thingies that determine my experimental predictions and the thingy that determines my experimental results. I call the former thingies 'beliefs', and the latter thingy 'reality'.
You ought to admit that the statement 'there is "the thingy that determines my experimental results"' is a belief. A useful belief, but still a belief. And forgetting that sometimes leads to meaningless questions like "Which interpretation of QM is true?" or "Is wave function a real thing?"
0
Why? Didn;t anyone ever see results that conflict with their beliefs?
0
Yes... and...? Feel free to explicate the missing steps between what I wrote and what you did.
0
So what was it that conflicted with their beliefs, when they saw a result that conflicte with their beliefs?
-2
The actual belief is "This thingy which determines my experimental results is internally consistent and the rules governing it are time-invariant."
Where are your experimental results? Where are your beliefs? If they aren't the same thing, how can you compare them?
And finally: What would you expect to see if the thingy which determined the results of your experiments didn't have the qualities you ascribe to it? Try to avoid putting the question a meta-level up; my conclusion is that there is no evidence which doesn't support the premise that what I call reality is capricious and transient- but that if it is, there is no change in expected outcome from any decision I can make.
-5
8
https://corticalchauvinism.files.wordpress.com/2014/04/dse232_1_004i.jpg
I think...
The first image in this post does not show up anymore. The URL in the source code, http://labspace.open.ac.uk/file.php/4771/DSE232_1_004i.jpg , needs to be replaced by http://labspace.open.ac.uk/file.php/8398/DSE232_1_004i.jpg . However, perhaps it would be best to host somewhere other than labspace.open.ac.uk, if they will continue to frequently reorganize their files.
(Feel free to delete this comment when the issue is fixed.)
Also on the issue of insisting that all facts be somehow reducible to facts about atoms or whatever physical features of the world you insist on consider the claim that you have experiences.
As Chalmers and others have long argued it's logically coherent to believe in a world that is identical to ours in every 'physical' respect (position of atoms, chairs, neuron firings etc..) but yet it's inhabitants simply lacked any experiences. Thus, the belief that one does in fact have experiences is a claim that can't be reduced to facts about atoms or whatever.
Wor...
1
You're basically attacking (one of?) the strongest tenet of LessWrong culture with practically no basis other than "presumably", "Chalmers and others" as an authority (Chalmers' words are not taken as Authority here, and argument trumps authority anyway), and some vague phrasings about "physical terms", "by it's very nature [sic]", "can't be reduced" and "properties of quantum fields".
My own best interpretation is that you're making a question-begging ontological argument that information, learning, knowledge, consciousness or whatever other things are implied by your vague wording are somehow located in separate magisteria.
Also, please note that, as discussed in more details in the other articles following this one, Eliezer clearly states that these epistemic techniques don't rule out a priori any concepts just because they don't fit with some materialistic physical laws one assumes to be true.
First a little clarification.
The contribution of Tarski was to define the idea of truth in a model of a theory and to show that one could finitely define truth in a model. Separately, he also showed no consistent theory can include a truth predicate for itself.
As for the issue of truth-conditions this is really a matter of philosophy of language. The mere insistence that there is some objective fact out there that my words hook on to doesn't seem enough. If I insist that "There are blahblahblah in my room." but that "There are no blahblah...
0
Yes.
Can we verify or falsify it? Yes, iff it somehow constricts possible realities in a manner that is exclusively different from other hypotheses and in-principle observable from our reference frame(s) assuming we eventually obtain the means to make relevant observations.
3
It's actually called the Many Worlds INTERPRETATION, and what interpretation means in this case is specifically that there is not experimental test to distinguish it from interpretation. Theory=thing you can test, interpretation=thing you can't test. Indeed, EY's arguments for MWI are not empirical and are therefore his own version of Post Utopianism.
0
Retracted
The river side illustration is inaccurate and should be much more like the illustration right above (with the black shirt replaced with a white shirt).
4
I think this includes too much. It would includes meaningless beliefs. "Zork is Pork." True or false? Consistency seems to me to be, at best, a necessary condition, but not a sufficient one.
1
Could you give me an example of a belief that is consistent with reality but false?
1
I'm definitely having more trouble than I expected. Unicorns have 5 legs... does that count? You're making me doubt myself.
0
Cool. : )
Is "Unicorns have 5 legs" consistent with reality? I would be quite surprised to find out that it was.
0
Well it doesn't seem to be inconsistent with reality.
0
It doesn't even have any referents to reality. It's not even a statement about whatever "reality" we live in, to the best of my knowledge. If it does mean five-leggedness of unicorn creatures with the implication of the existence of possible-existence of such creatures in reality, then it is false, but it's inconsistent with what we know of reality, since there's no way such a creature would exist.
...I think, anyway. Not quite sure about that second part.
-1
The non-existence of unicorns makes the claim that they have legs, in whatever number, inconsistent with reality.
0
Counterfactuals? If there's a unicorn on Mars, then I'm the president. Though it depends on what gets included in the term "reality."
2
Neither of those things are examples of beliefs that are consistent with reality but false. The belief "If there's a unicorn on Mars, then I'm the president" is true, consistent with reality but also utterly worthless.
Counterfactuals are also not false. (Well, except for false counterfactual claims.) A (well formed) counterfactual claim is of the type "Apply this specified modifier to reality. If that is done then this conclusion will follow.". Such claims can be true, albeit somewhat difficult to formally specify.
4
I didn't mean that all counterfactuals are false, I meant a specific example of a counterfactual claim that is false - e.g. If you put a unicorn on Mars, then I'll become president (which expresses the example I meant to give in the grandparent, not a logical if-then).
(Apologies for not clearly saying that)
2
Thankyou, I understand what you are saying now.
For what it is worth I would describe that counterfactual claim as inconsistent with reality and false. That is, when instantiating the counterfactual using the counterfactual operation as reasonably as possible it would seem that reality as I know it is not such that the modified version would result in the consequences predicted.
(Note that with my understanding of the terms in question I think it is impossible to have something consistent with reality and false so it is unsurprising that given examples would not appear to me to meet those criteria simultaneously.)
2
Yeah, I think I agree after thinking about it a bit - I mean, why wouldn't we define the terms that way?
0
I take "consistent" to mean roughly "does not contain a contradiction", so "a belief that is consistent with reality" would mean something like "if you take all of reality as a collection of facts, and then add this belief, as a fact, to that collection, the collection won't contain a contradiction." It seems to me, if this is a fair representation of the concept, that some beliefs about the future are consistent with reality, but false. For example:
Humanity will be mining asteroids in 2024.
This is consistent with reality: there is at least one company talking about it, there are no obvious impossibilities (there are barriers, but we recognise they can be overcome with engineering)... but it's very probably false.
0
Mutualy inconsistent statements can be consistent with known facts, eg Lady MacBeth had 2 chidren, Ldy MacBeth had 3 children...but that just exposes the problem with correspondence. if it isn't consistency...what is it?
0
Better example, maybe: the continuum hypothesis
0
Tell me what Zork is and i'll let you know. : )
0
Zork is a classic computer game (or game series, or game franchise; usage varies with context) from c.1980.
And yet it seems to me - and I hope to you as well - that the statement "The photon suddenly blinks out of existence as soon as we can't see it, violating Conservation of Energy and behaving unlike all photons we can actually see" is false, while the statement "The photon continues to exist, heading off to nowhere" is true.
I remember when you drew this analogy to different interpretations of QM and was thinking it over.
The way I put it to myself was that the difference between "laws of physics apply" and "everything ac...
2[anonymous]
If I understand it correctly, (and I am not sure, feel free to correct me.) it occurs to me that belief may have a very unusual consequence indeed, which seems to be believing that "The photon continues to exist, heading off to nowhere." is true implies that you should also believe the Probability of world P1 is greater than Probability of world P2 below.
P1: "You are being simulated on a supercomputer which does not delete anything past your cosmological horizon."
P2: "You are being simulated on a supercomputer which deletes anything past your cosmological horizon."
Which sounds like a very odd consequence of believing "The photon continues to exist, heading off to nowhere." is true, but as far as I can tell, it appears to be the case.
1
Non-conditional probabilities are not the sole determinants of conditional probabilities. You're conflating P(photon exists) with P(photon exists|simulated universe).
Your conclusion does not logically follow from your premise. You need to separate out your conditional probabilities.
I'm also not sure the belief is particularly odd: why should you be at the center of the simulation? What makes your horizon more special than someone else's, or the union of all observer's horizons?
0[anonymous]
Thanks, I suspected that idea needed more processing.
I'm going to be honest and admit that I do not actually know how to write in a P(photon exists|simulated universe) style manner, and when I tried to find out how, I failed that as well because didn't know the name and it didn't appear under any of the names I guessed. Otherwise, I would try to rewrite my idea in that format and doublecheck the notation.
To unpack what I meant when I said the belief was odd/very unusual, It might have been more clear to say "This isn't necessarily wrong, but it doesn't seem to be an answer I would expect, and this thing I thought of just now appears to be my only justification for it, even though I haven't yet seen anything wrong.
And as for why I picked that particular horizon, I think I was thinking of it primarily as a "Eliezer said this was true. If that is the case, what would make it false? Well, if I was living in a simulated world and things were getting deleted when I could never interact with them again, then it would be false." but as you pointed out, I need to fix the thought anyway.
1
P(A|B) should be read as "the probability of A, given that B is true" or, more concisely, "P of A given B". Search terms like [conditional probability(http://en.wikipedia.org/wiki/Conditional_probability) should get you started. You'll probably also want to read about Bayes' Theorem.
Thus, after the photon goes past a certain point, there are no experimental consequences whatsoever, ever, to the statement "The photon continues to exist, rather than blinking out of existence."
Probably because your definition of existence is no good. Try a better one.
8
That's an attempt to dismiss epistemic rationality by arguing that only instrumental rationality matters.
I suppose that's true by certain definitions of "matters", but it ignores those of us who do assign some utility to understanding the universe itself, and therefore at least partially incorporate the epistemic in the instrumental....
Also, if I die tomorrow of a heart attack, I think it's still meaningful to say that the rest of the planet will still exist afterwards, even though there won't exist any experimental prediction I can make and personally verify to that effect. I find solipsism rather uninteresting.
4
No. Please note that the terminology here is overloaded, hence it can cause confusion.
Instrumentalism, in the contex of epistemology, does not refer to instrumental rationality. It is the position that concepts are meaningful only up to the extent that they are useful to explain and predict experiences.
In the instrumentalist framework, you start with an input of sensorial experiences and possibly an output of actions (you may even consider your long-term memories as a type of sensorial experiences). You notice that your experiences show some regularities: they are correlated with each others and with your actions. Thus, put forward, test, and falsify hypotheses in order to build a model that explains these regularities and helps you to predict your next experience.
In this framework, the notion that there are entities external to yourself is just a scientific hypothesis, not an assumption.
Epistemological realism, on the other hand, assumes a priori that there are external entities which cause your experiences, they are called "Reality" or "the Truth" or "Nature" or "the Territory".
Believing that abstract concepts, such as mathematical axioms and theorems, are also external entities, is called Platonism. That's for instance, the position of Roger Penrose and, IIUC, Eliezer Yudkowsky.
The distinction between assuming a priori that there is an external world and merely hypothesizing it may appear of little importance, and indeed for most part it is possible to do science in both frameworks. However, the difference shows up in intricate issues which are far removed from intuition, such as the interpretaion of quantum mechanics:
Does the wavefunction exist? For an instrumentalist, the wavefunction exists in the same sense that the ground beneath their feet exists: they are both hypothesis useful to predict sensorial experiences. For a realist, instead, it makes sense to ponder whether the wavefunction is just in the map or also in the territory.
2
Epistemic rationality is a subset of instrumental rationality, to the extent that you value the truth.
-- Sark
(this allows the universe to keep existing after I die).
-2
No, that's the statement that epistemic rationality is based on instrumental rationality.
Indeed, no good model predicts that a death of one individual result in the cessation of all experiences for everyone else. Not sure what strawman you are fighting here.
Except as a psychological phenomenon, maybe.
-1
Okay, then I've probably misunderstood what definition you meant to give to "exist". The comment you linked talked about reliably predicting future experiences, and I'll reliably not be experiencing a universe after my death -- so doesn't that mean that the universe won't exist if I shared your definition of "exist"?
That conclusion also seemed to me to follow from your complaint about EY's definition involving photons that keep on existing after we no longer get to experience them.
Anyway, whatever confusion I have about the meaning you attempted to communicate, it was an honest one.
0
I don't see why. A half-decent model would not center on a single person, and the definition given does not say that "future experiences" are those of a specific person. Unless, of course, the model in question strives to describe this person's sensory experience, in which case, yes, you likely stop sensing the universe after you are gone.
0
You're applying TheOtherDave's definition in a manner that he himself has disavowed. He believes, for instance, that on his account the existence claims of simpler theories should be believed over the existence claims of more complex theories, even if those theories make the same experimental predictions. This would legitimize Eliezer's claim that the photon continues to exist, rather than blinking out, since it is a simpler model. See the discussion following this comment of mine.
0
Yes, simpler models out of several equivalent ones are preferable, no argument there. I never said otherwise, that would be silly. Here I define "simpler" instrumentally, those which require less work to make the same set of predictions. Please don't strawman me,
2
Sorry! Any strawmanning was unintentional. However, I'm not so sure that there was strawmanning. I meant "simpler" in terms of some appropriately rigorous version of Occam's razor. This seems different from your conception of "simpler". A simpler theory in my sense need not involve less work to make the same predictions. The standard usage of "theoretical simplicity" on LW is more in line with my conception than yours, so I have good reason to believe that this is the way TheOtherDave was using the word.
Just to make sure: do you think simpler models (in my sense) are preferable? Or do you think our two senses are in fact equivalent?
4
It's kind of entertaining watching this exchange interpreting my earlier comments, and I'm sort of reluctant to disturb it, but FWIW my usage of "simplicity" was reasonably well aligned with your conception, but I'm not convinced it isn't well-aligned with shminux's, as I'm not really sure what "work" refers to.
That said, if it refers to cognitive effort, I think my conception is anti-aligned with theirs, since I would (for example) expect it to be more cognitive effort to make a typical prediction starting from a smaller set of axioms than from a larger set of (mutually consistent) axioms, but would not consider the larger set simpler.
0
My guess is that the larger set will have some redundancy, i.e. some of the axioms would be in fact theorems. But I don't know enough about that part of math to make a definitive statement.
0
I agree that if it's possible, within a single logical framework F, to derive proposition P1 from proposition P2, then P1 is a theorem in F and not an axiom of F... or, at the very least, that it can be a theorem and need not be an axiom.
That said, if it's possible in F to derive some prediction P3 from either P1 or P2, it does not follow that it's possible to derive P1 from P2.
-1
I'm yet to see a workable version of it, something that does not include computing uncomputables and such. I'd appreciate f you point me to a couple of real-life (as real as I admit to it to be, anyway) examples where a rigorous version of Occam's razor was successfully applied to differentiating between models. And no, the hand-waving about a photon and the cosmological horizon is not rigorous.
Again, a (counter)example would be useful here.
That depends on whether simpler models in your sense can result in more work to get to all the same conclusions. I am not aware of any formalization that can prove or disprove this claim.
Why is it accepted that experiments with reality prove or disprove beliefs?
It seems to me that they merely confirm or alter beliefs. The answer given to the first koan and the explanation of the shoelaces seem to me to lead to that conclusion.
"...only reality gets to determine my experimental results."
Does it? How does it do that? Isn't it the case that all reality can "do" is passively be believed? Surely one has to observe results, and thus, one has belief about the results. When I jump off the cliff I might go splat, but if the clif...
3
Well, in one sense it isn't accepted... not if you want "prove" to mean something monolithic and indisputable. If a proposition starts out with a probability between 0 and 1, no experiment can reduce that probability to 0 or raise it to 1... there's always a nonzero probability that the experiment itself was flawed or illusory in some way.
But we do accept that experiments with reality give us evidence on the basis of which we can legitimately increase or decrease our confidence in beliefs. In most real-world contexts, that's what we mean by "prove": provide a large amount of evidence that support confidence in a belief.
So, OK, why do we accept that experiments do that?
Because when we predict future experiences based on the results of those experiments, we find that our later experiences conform to our earlier predictions.
Or, more precisely: the set of techniques that we classify as "reliable experiments"are just those techniques that have that predictive properties (sometimes through intermediate stages, such as model building and solving mathematical equations). Other, superficially similar, techniques which lack those properties we don't classify that way. And if we found some superficially different technique that it turned out had that property as well, we would classify that technique similarly. (We might not call it an "experiment," but we would use it the same way we use experiments).
Of course, once we've come to trust our experimental techniques (and associated models and equations), because we've seen them work over and over again on verifiable predictions, we also develop a certain level of confidence in the _un_verifiable predictions made by the same techniques. That is, once I have enough experience of the sun rising in the morning that I am confident it will do tomorrow, (including related experiences, like those supporting theories about the earth orbiting the sun etc., which also serve to predict that event), I can be confident that it will
0
"Throughout this process, what I'm doing is using my observations as evidence for various propositions. "Reality" is my label for the framework that allows for those observations to occur, so what we call this process is "observing reality."
"What's confusing?"
It seems to me that given this explanation, we can never know reality. We can only ever have a transient belief in what it is, and that belief might turn out to be wrong. However many 9's one adds onto 99.999% confident, it's never 100%.
From the article: "Isn't all this talk of 'truth' just an attempt to assert the privilege of your own beliefs over others, when there's nothing that can actually compare a belief to reality itself, outside of anyone's head?"
I think the article was, in part, setting out to debunk the above idea, but surely the explanation you have provided proves it to be the case? That's why I'm confused.
0
That's progress.
0
Yes, that's true.
Mm.
It sounds to me like we're not using the word "reality" at all consistently in this conversation.
I would recommend trying to restate your concern without using that word. (Around here this is known as "Tabooing" the word.)
0
Thanks for engaging on this - I'm finding it educating. I'll try your suggestion but admit to finding it hard.
So, there's a Chinese rocket-maker in town and Sir Isaac Newton has been offered the ride of his life atop the rocket. This is no ordinary rocket, and it's going to go really, really fast. A little boy from down the road excitedly asks to join him, and being a jolly fellow, Newton agrees.
Now, Newton's wife is pulling that funny face that only a married man will recognise, because she's got dinner in the oven and she knows Newton is going to be late home again. But Newton is confident that THIS time, he's going to be home at precisely 6pm. Newton has recently become the proud owner of the world's most reliable and accurate watch.
As the rocket ignites, the little boy says to Newton, "The vicar told me that when we get back, dinner is going to be cold and your wife is going to insist that your watch is wrong."
Now, we all now how that story plays out. Newton had been pretty confident about his timepiece. 99.9999%, in fact. And when they land, lo and behold his watch and the church clock agree precisely and dinner is very nice.
Er, huh?
Because in fact, the child is a brain in a vat, and the entire experience was a computer simulation, an advanced virtual reality indistinguishable from the real thing until someone disconnects him.
That's the best I can do without breaking the taboo.
1
You've mostly lost me, here.
Reading between the lines a little, you seem to be suggesting that if Newton says "It's true that we returned in time for dinner!" that's just an attempt to assert the privilege of his beliefs over the boy's, and we know that because Newton is unaware of the simulators.
Yes? No? Something else?
If I understood that right, then I reject it. Sure, Newton is unaware of the simulators, and may have beliefs that the existence of the simulators contradicts. Perhaps it's also true that the little boy is missing two toes on his left foot, and Newton believes the boy's left foot is whole. There's undoubtedly vast numbers of things that Newton has false beliefs about, in addition to the simulators and the boy's foot.
None of that changes the fact that Newton and the boy had beliefs about the rocket and the clock, and observed events supported one of those beliefs over the other. This is not just Newton privileging his beliefs over the boy's; there really is something (in this case, the programming of the simulation) that Newton understands better and is therefore better able to predict.
If "reality" means anything at all, the thing it refers to has to include whatever made it predictably the case that Newton was arriving for dinner on time. That it also includes things of which Newton is unaware, which would contradict his predictions about other things were he to ever make the right observations, doesn't change that.
0
I thought that 99.999999.... actually does equal 100, no?
5
There is no instantiation of "however many" with an integer, n, that results in the "equals 100%" result (because then n+1 would result in more that 100% which is just way off). There are some more precise things we can say along the lines of "limit as n approaches infinity where..." that express what is going on fairly clearly.
Writing the "99.9 repeating" syntax with the dot does mean "100" according to how the "writing the dot on the numbers" syntax tends to be defined, which is I think what you are getting at but seems different to what Berry seems to be saying.
0
Ah, I get it now, thanks.
2
Yes, but us being finite creatures, we cannot ever add more than a finite number of 9's.
1
And one of the beliefs they've confirmed is "reality is really real, it isn't just a belief." :-)
No. If that's all it could do then it would be indistinguishable from fiction. It's not, we know it's not, and I bet that you yourself treat reality differently than you treat fiction, thus disproving your claim.
0
"It's not, we know it's not, and I bet that you yourself treat reality differently than you treat fiction, thus disproving your claim."
How do we know it's not? You might say that I know that the table in front of me is solid. I can see it, I can feel it, I can rest things on it and I can try but fail to walk through it. But nowadays, I think a physicist with the right tools would be able to show us that, in fact, it is almost completely empty space.
So, do I treat reality different from how I treat fiction? I think the post we are commenting on has finally convinced me that there is no reality, only belief, and therefore the question is untestable. I think that is the opposite of what the post author intended?
History does tend to suggest that anyone who thinks they know anything is probably wrong. Perhaps those here are less wrong, but they - we - are still wrong.
"And one of the beliefs they've confirmed is "reality is really real, it isn't just a belief." :-)"
Hah! Exactly! The experiments confirm a belief. A confirmed belief is, of course, still a belief. If your belief that reality is really real is confirmed, you now have a confirmed belief that reality is really real. That's not the same thing as reality being really real, though, is it?
;-)
6
So f***ing what? What does solidity have to do with amount of empty space? If according to your definition of solid, ice is less solid than water because it contains more empty space, your definition of solid is broken.
5
Yes. I bet that if a fire happens you'll call the fire-brigade, not shout for Superman. That if you want to get something for Christmas, you'll not be writing to Santa Claus.
No matter how much one plays with words, most people, even philosophers, recognize reality as fundamentally different to fiction.
This is playing with words. "Solidity" has a macroscale meaning which isn't valid for nanoscales. That's how reality works in the macroscale and the nanoscale, and it's fiction in neither. If it was fiction then your ability to enjoy the table's solidity would be dependent on your suspension of disbelief.
The operative word here is "less". Here's a relevant Isaac Asimov quote: "When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together."
You are effectively being "wronger than both of them put together"
1 and 0 aren't probabilities, but you're effectively treating a statement of 99.999999999% certainty as if it's equivalent to 0.000000000000001% certainty; just because neither of them is 0 or 1.
That's pretty much an example of "wronger than both of them put together" that Isaac Asimov described...
0[anonymous]
"most people, even philosophers, recognize reality as fundamentally different to fiction."
That statement may or may not be correct, but even if it is correct, it has limited relevance to whether reality is different to belief unless all beliefs are fictions. They might all be fictions, but that assertion is untestable.
Perhaps you intend to suggest that most people recognise reality as fundamentally different to belief? Well, that would be a more interesting statement, but I will contend that if they do, they are wrong. Are you familiar with the brain in a vat? I'm new here and kind of assumed that anyone here is. If so, then I cannot understand why anyone here would think that reality exists at all independently of belief. There is no evidence for reality other than belief. How can there possibly be? The idea is absurd, surely? How could such evidence enter our consciousness other than through believing our senses?
-1
Using the same word in triplicate to make your point does not make the point more convincing.
0
It doesn't seem to be intended to be more convincing, or the point for that matter. That relies on the rest of the sentence.
meditation answer to “What rule could restrict our beliefs to just propositions that can be meaningful, without excluding a priori anything that could in principle be true?”
Rule: that we continue to use the words true and truth to describe if something corresponds to reality within a wider context of prediction, experimentation and action, and not solely observation. In this case we expand the senses of perception to include rational experimentation as part of how we evaluate true or not true. The weird part about this is an underlying assumption that real...
Curated and popular this week