I recently posted about doing Celtic Knots on a Hexagonal lattice ( https://www.lesswrong.com/posts/tgi3iBTKk4YfBQxGH/celtic-knots-on-a-hex-lattice ).
There were many nice suggestions in the comments. @Shankar Sivarajan suggested that I could look at a Einstien lattice instead, which sounded especially interesting. ( https://en.wikipedia.org/wiki/Einstein_problem . )
The idea of the Einstein tile is that it can tile the plane (like a hexagon or square can), but it does so in a way where the pattern of tiles never repeats.
The tile I took from Wikipedia looks like this:
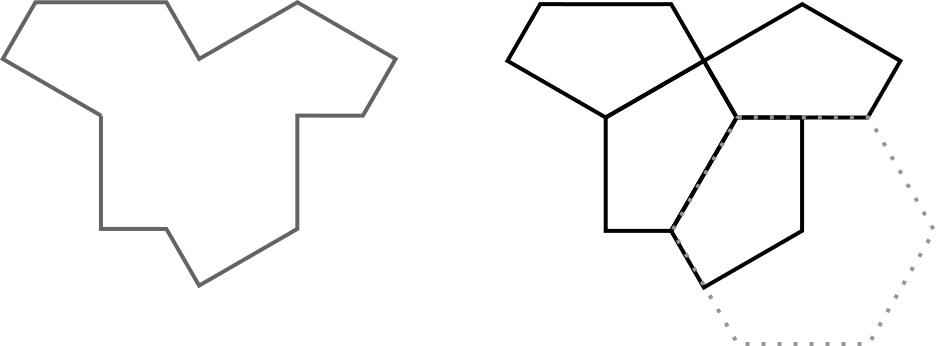
On the left is the full tile. On the right is a way of decomposing it into four-thirds of a hexagon.
For some reason I think of it as a lama. On the left top is its head, facing left. On tie right top its its tail. The squarish bit coming down is the legs.
First problem: the tile has 13 sides. So if we run a string into/out of every edge we are going to have a loose end. Second problem, sometimes a face in the tiling touches a corner:
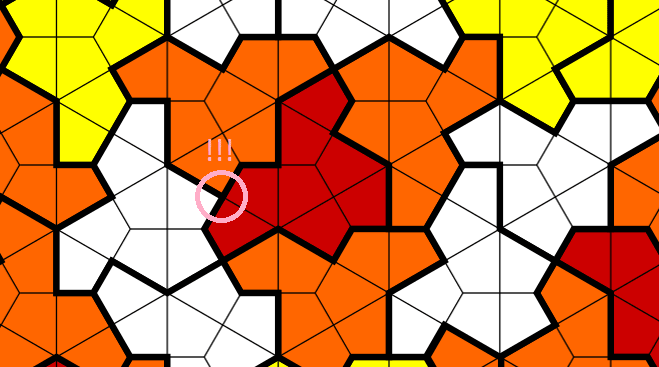
Image from Wikipedia. In the pink circle the face of the red tile connects to a corner between the orange and white ones. This is a problem, if we had a string going off that edge of the red tile it would get split.
The solution is to identify a subset of the edges to put strings on, where this will never happen. The hex grid underlay on Wikipedia reveals a strategy - take only those facets touching a hexagon separator line. IE for each of the 4 thirds of a hexagon, the two long edges of those third pieces, are used. This gives 6 total per tile (an even number, woo!), meaning that the connectors joining each in/out to each other fill this table:
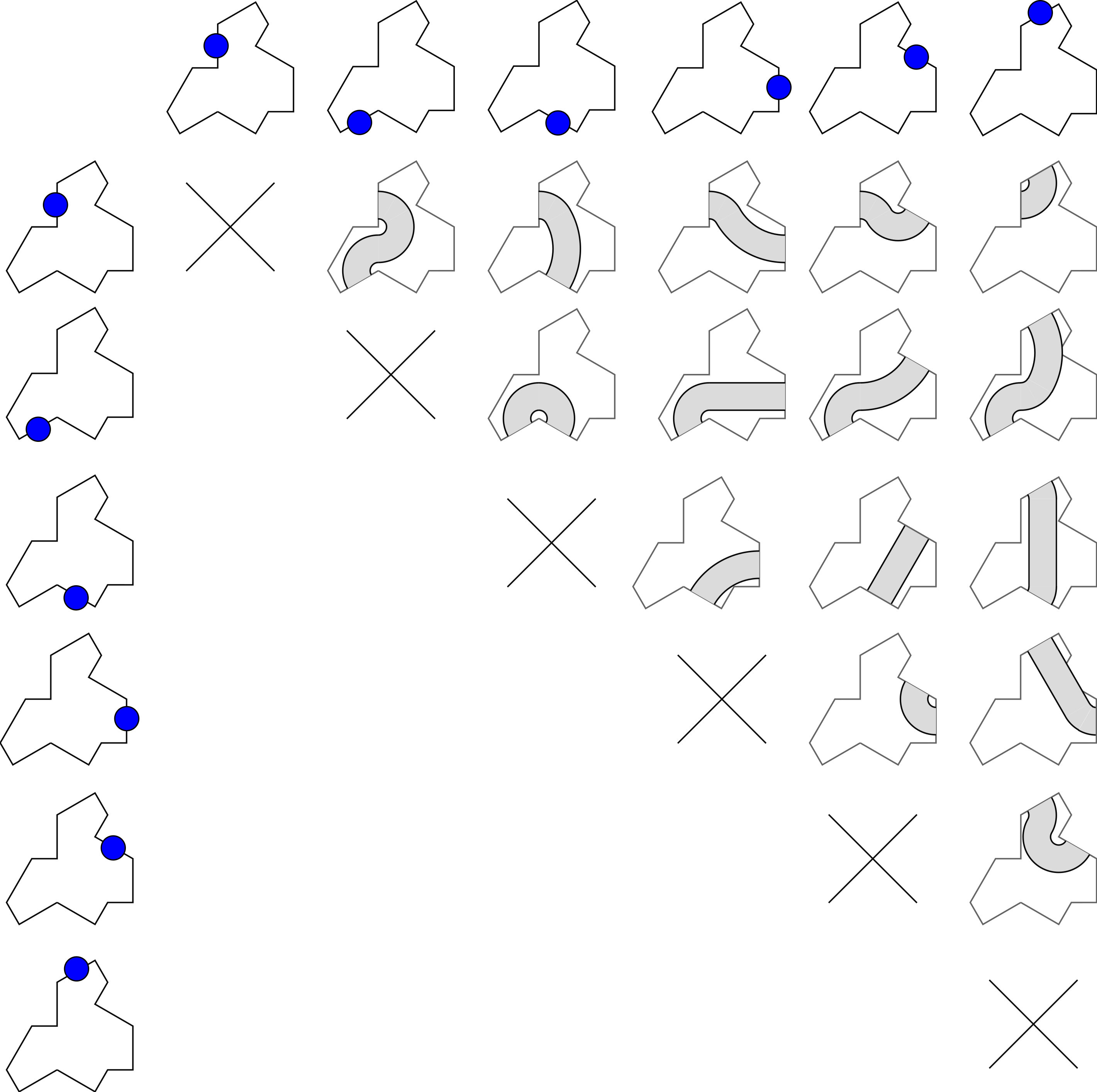
(Each entry point can connect to any exit except itself.)
Notice that a couple of the ropes trespass slightly outside the tile. This seems like it will be fine, if it does touch a rope in another tile it can just go over or under it.
Combining these connectors every possible way we get this tile set:
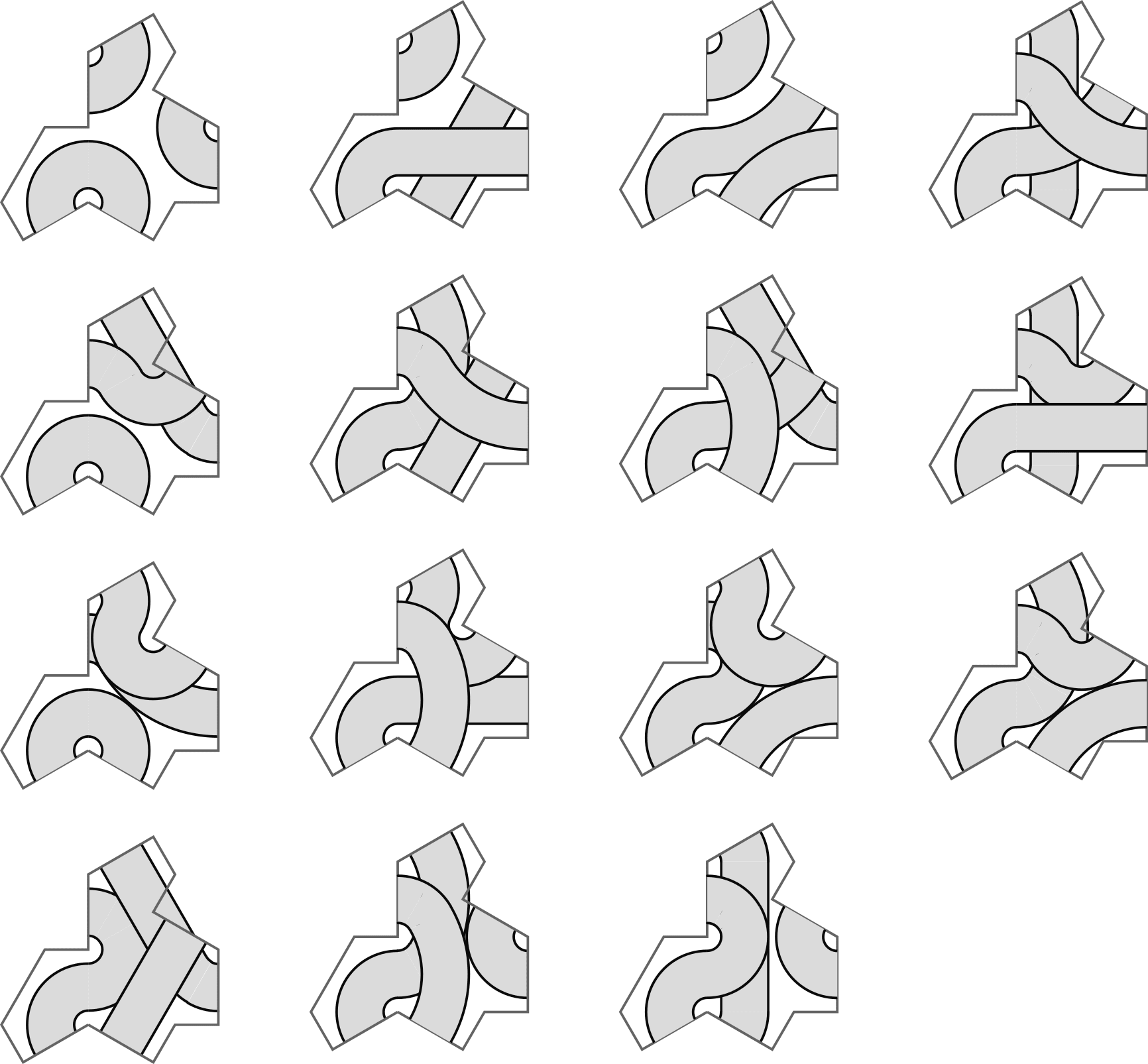
Pretty weird looking.
Using them to semi-randomly tile the plane using the pattern from Wikipedia we get something as weird as might be expected:
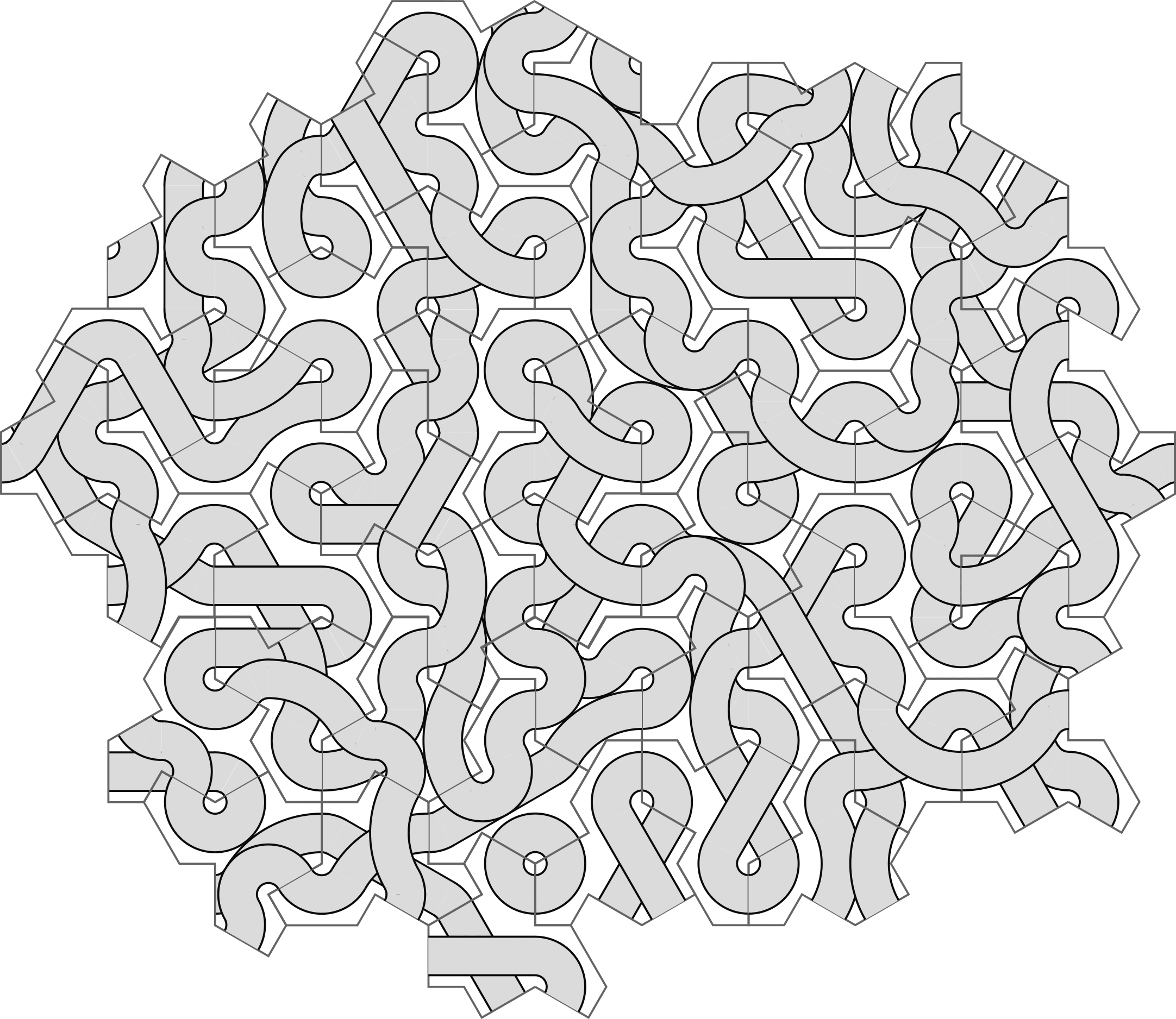

I like the "clover" that formed in the middle of the design.
One big downside compared to hexagons is I can't just put tiles down fluently, while concentrating on the aesthetics. After picking up a tile to use I typically spend 20+ seconds rotating and mirroring it while consulting the mapping scheme, before finally working out how it goes in. At that point I could do similar for a different tile and then pick the one that looked better, but my patience did not stretch so far as that. I am getting faster, and putting the map underneath helps, but its still not an effortless process like with hexagons.
Using copies of just one tile again and again is still chaotic looking, barring the obvious counter-example:
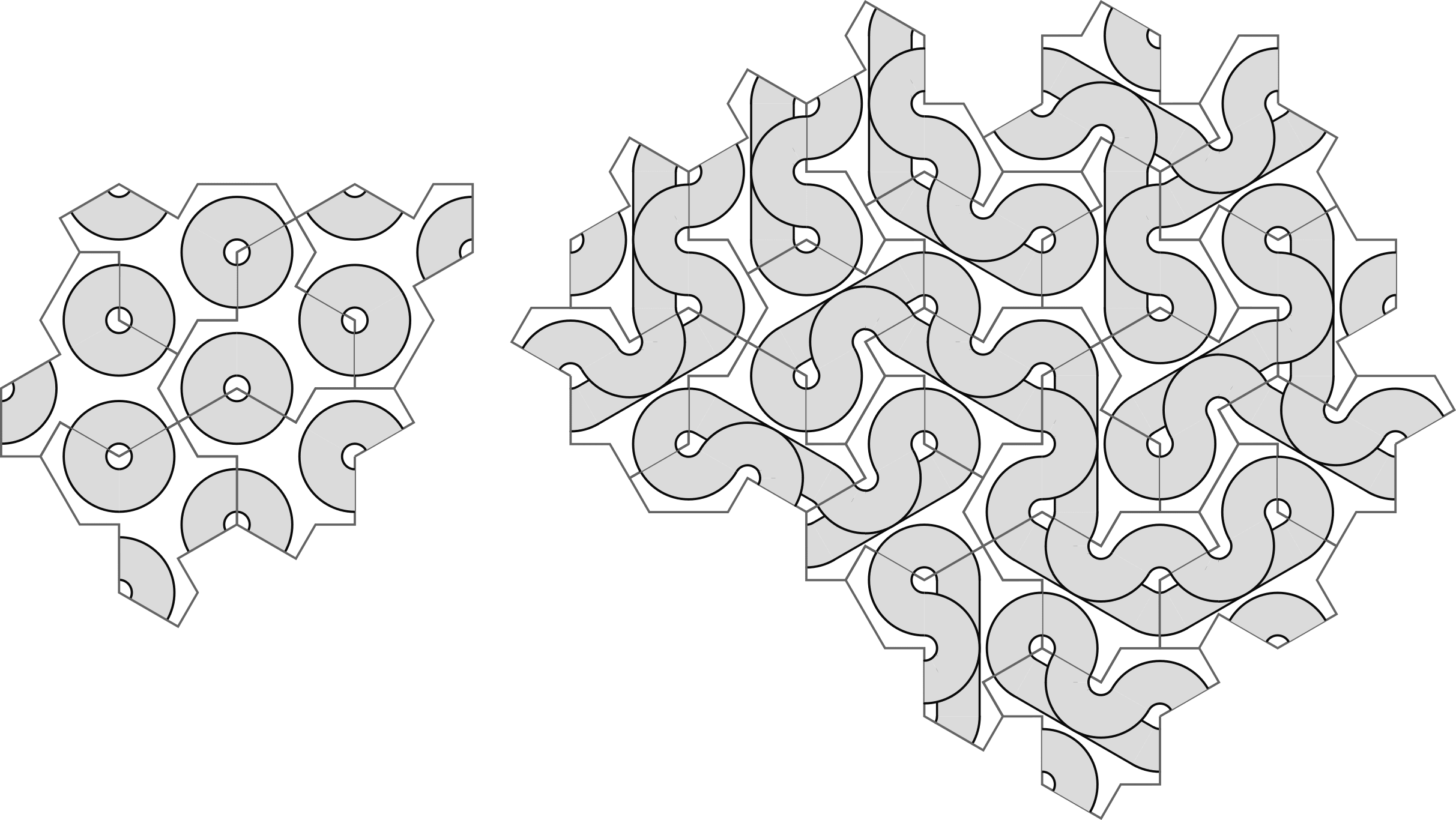
I added all this stuff to the shared folder(as inkscape .svg files) in case anyone wanted a play with the tiles. https://drive.google.com/drive/folders/1BS42moNocDLIwFGeEAESK0ttX4CANo-5




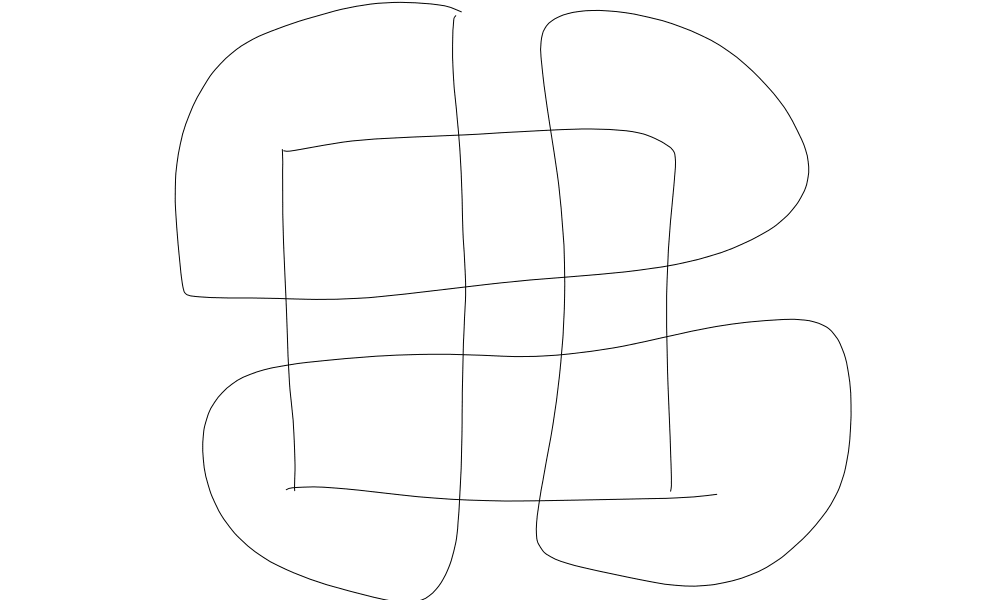
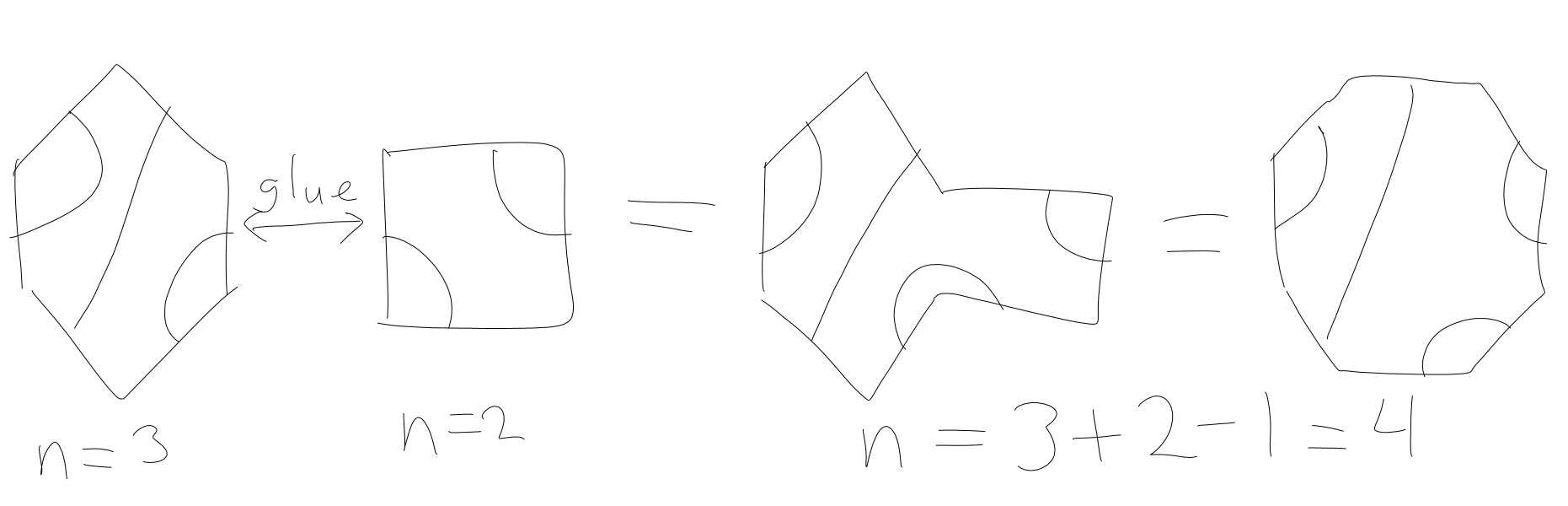
The sidelengths for the Einstein tile are all either 1 or √3, except for a single side of length 2. I think it makes more sense to treat that side as two sides, with a 180∘ angle between them. Then you would get fourteen entry/exit points:
The aperiodic tiling from the paper cannot be put onto a hexagonal grid, and some of the tiles are flipped vertically, so you need every edge to have an entry/exit to make a Celtic knot out of it. Also, I would recommend using Tile(1,1) rather than Tile(1,√3) so the arcs turn out pretty:
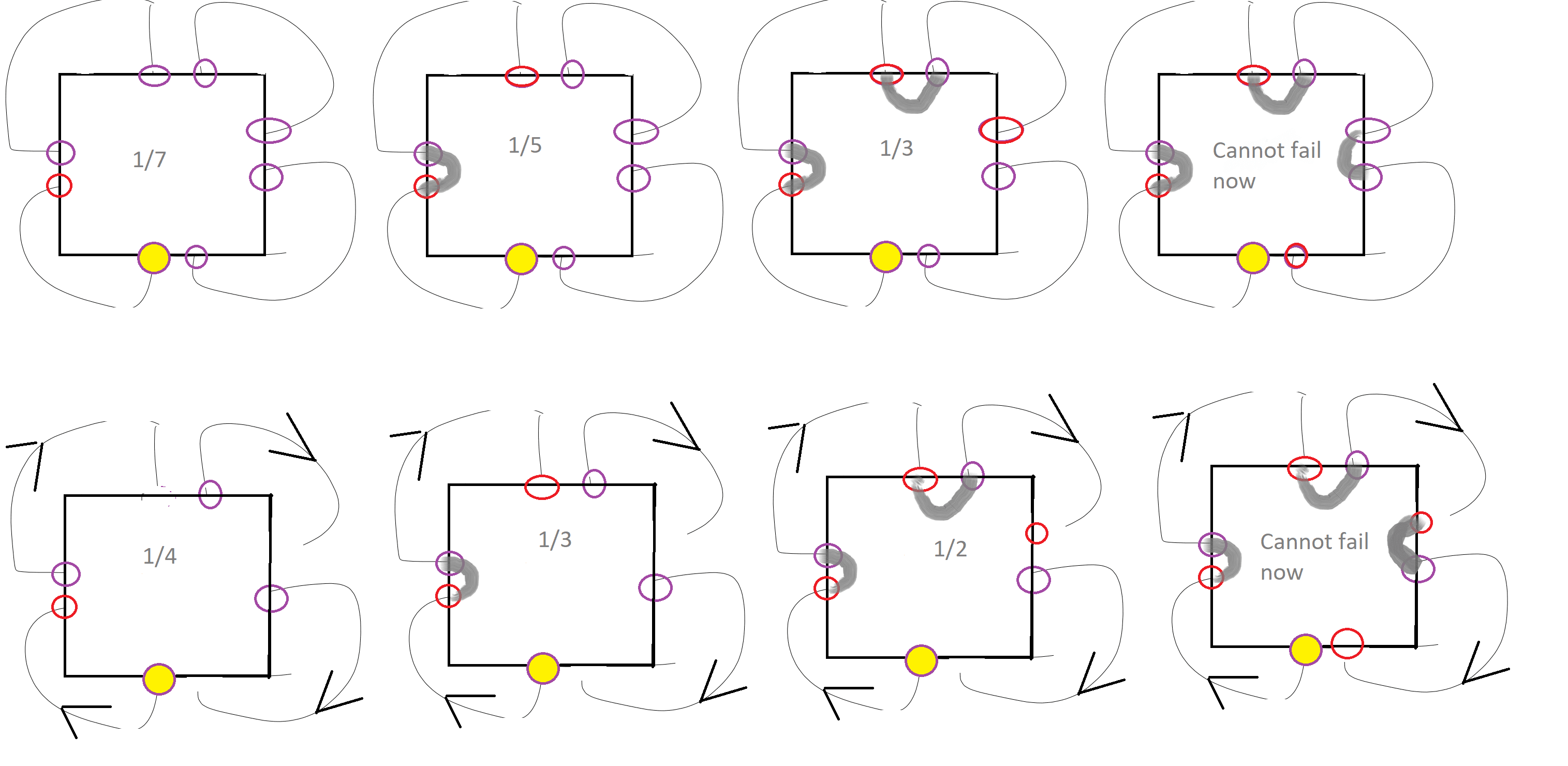
The bottom row is close to what I imagine, but without IO ports on the same edge being allowed to connect to each other (though that is also an interesting problem). These would be the three diagrams for the square:
The middle one makes a single loop which is one-third of them, and n=4/2=2 in this case. My guess for how to prove the recurrence is to "glue" polygons together:
There are n+1 pairs of sizes (k,n+1−k) we can glue together (if you're okay with 2-sided polygons), but I haven't made much progress in this direction.... (read more)