New Comment
Thanks for writing and sharing this dialogue on LessWrong! I really enjoyed it, and I think the questions about how and when neural networks generalise are very interesting (in particular because of the interplay with questions about when and whether we should expect things to “generalise to agents”).
I thought I’d mention a couple of things that I particularly enjoyed about this dialogue, and share my intuitive story about grokking. I also had some specific questions and clarifications, which I’ll scatter through some sibling comments.
The reasoning transparency around which of your views had evolved in conversation or how much of a given paper you’ve read or (especially!) understood. It’s pretty easy for me to feel like if I’m going to try and join some conversations based on theory papers, I have to read and understand them completely in order to contribute. But seeing you be epistemically resourceful with some papers you were less familiar with relaxed me a bit.
I also like how you were both willing to put yourself out there with respect to your intuitions for grokking. I have felt somewhat similarly to Dmitry with respect to “but like, wouldn’t a generalising circuit just warm up slowly then get locked in? What’s the confusion?”, or Kaarel on “generalising circuits are more efficient”. That then made the questions like “well is this a sigmoid growth curve or a random walk followed by rapid scale up?” or “why does memorisation sometimes happen significantly earlier?” or “why don’t the circuits improve loss linearly such that you learn each of them a bit?” much easier for me to grasp, because I’d been “brought along” the path.
I thought I would throw in my intuitive story as well (which I think is largely similar to the ones in the post). It only really works with regularisation, and I don’t know much about ML, so perhaps I’ll learn why this can’t work.
The initialised network has at least a few “lottery tickets” that more-or-less predict some individual data points. They have good gradients to get locked-in at the beginning. After a few such points are learned, the classification loss is not as concentrated on the generalising solution (which is partially just getting the right answer on data points where we already get the right answer).
In fact, the generalising solution might be partially penalised on the data points where we’ve memorised solutions, as it continues to push on high probability tokens, slightly skewing the distribution (or worse if we’re regressing). But there’s probably still overall positive gradient on the generalising solutions.
As the generalising circuit continues to climb, the memorising circuits are less-and-less valuable, and start to lose out against the regularisation penalty. As the memorising circuits start to decline, the generalising circuit gets stronger gradients as it becomes more necessary.
Ten months later, which papers would you recommend for SOTA explanations of how generalisation works?
From my quick research:
- "Explaining grokking through circuit efficiency" seems great at explaining and describing grokking
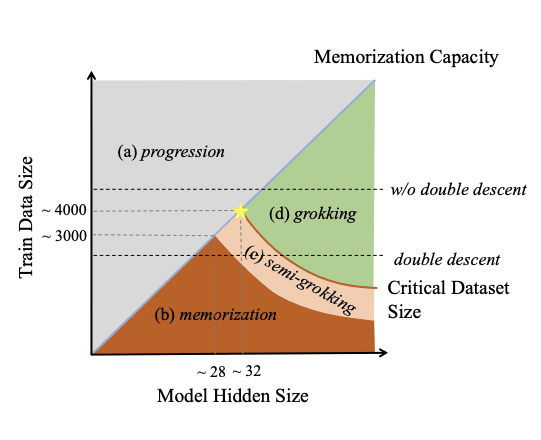
- "Unified View of Grokking, Double Descent and Emergent Abilities: A Comprehensive Study on Algorithm Task" proposes a plausible unified view of grokking and double descent (and a guess at a link with emergent capabilities and multi-task training). I especially like their summary plot:
just note that at a noisy configuration, you would expect "learnable directions" to be very noisy, and largely cancel each other out, so the gradient will be predominantly noise from the perspective of the circuits that are eventually learned
I think this is saying something like “parameters participate in multiple circuits and the needed value of that parameter across those circuits is randomly distributed”. Is that right?
I think that when we talk about regularization in some kind of context of "efficiency", we should include implicit regularization of this type and any other phenomenon that encourages lower-weight-norm solutions.
It does seem like small initialisation is a regularisation of a sort, but it seems pretty hard to imagine how it might first allow a memorising solution to be fully learned, and then a generalising solution. Maybe gradient descent in general tends to destroy memorising circuits for reasons like the “edge of stability” stuff Dmitry alludes to. But is the low initial weight norm playing much role there? Maybe there’s a norm-dependent factor?
It does seem like small initialisation is a regularisation of a sort, but it seems pretty hard to imagine how it might first allow a memorising solution to be fully learned, and then a generalising solution.
"Memorization" is more parallelizable and incrementally learnable than learning generalizing solutions and can occur in an orthogonal subspace of the parameter space to the generalizing solution.
And so one handwavy model I have of this is a low parameter norm initializes the model closer to the generalizing solution than otherwise, and so a higher proportion of the full parameter space is used for generalizing solutions.
The actual training dynamics here would be the model first memorizes a high proportion of the training data while simultaneously learning a lossy/inaccurate version of the generalizing solution in another subspace (the "prioritization" / "how many dimensions are being used" extent of the memorization being affected by the initialization norm). Then, later in training, the generalization can "win out" (due to greater stability / higher performance / other regularization).
In particular, in most unregularized models we see that generalize (and I think also the ones in omnigrok), grokking happens early, usually before full memorization (so it's "grokking" in the redefinition I gave above).
Is this just referring to something like the effective parameter count of the model — generalizing solutions are ones with a smaller effective parameter count — or is this referring to actual basins in the loss landscape?
Is the difference between “basin” and “effective parameter count” / “circuit” here that the latter is a minimum in a subset of dimensions?
Noticed thad I didn't answer Kaarel's question there in a satisfactory way. Yeah - "basin" here is meant very informally as a local piece of the loss landscape with lower loss than the rest of the landscape, and surrounding a subspace of weight space corresponding to a circuit being on. Nina and I actually call this a "valley" our "low-hanging fruit" post.
By "smaller" vs. "larger" basins I roughly mean the same thing as the notion of "efficiency" that we later discuss
in some sense, the model is underparametrized from the point of view of types of generalizing circuits
That is a pretty interesting idea! I’ll be interested to see if it works out. It seems like it’s possibly in tension with an SLT-like frame, where the multiple representation of generalising circuits is (in my limited understanding from a couple of hours of explanation) is a big part of the picture. Though the details are a little fuzzy.
To be clear, I have only cursory familiarity with SLT. But my thought is we have something like:
- Claim: the mechanism that favours generalising circuits involves the fact that symmetries mean they are overrepresented in the parameter space
- Claim: generalising algorithms are underrepresented in the parameter space
Which seem to be in tension. Perhaps the synthesis is that only a few of the generalising algorithms are represented, but those that are are represented many times.