This post has some ablation results around the thesis of the ICML 2024 Mech. Interp. workshop 1st prize winning paper: The Geometry of Categorical and Hierarchical Concepts in Large Language Models The main takeaway is that the orthogonality they observe in categorical and hierarchical concepts occurs practically everywhere, even at places where it really should not.

Overview of the original paper

A lot of the intuition and math around why they do what they do is shared in their previous work called The Linear Representation Hypothesis and the Geometry of Large Language Models, but let's quickly go over what the paper's core idea is:

They split the computation of a large language model (LLM) as:

$$P(y\mid x)=\frac{\exp \left(\lambda \right(x{)}^{\top }\gamma \left(y\right))}{{\sum }_{y^{\prime }\in \text{Vocab}}\exp \left(\lambda \right(x{)}^{\top }\gamma \left(y^{\prime }\right))}$$

where:
- $\lambda \left(x\right)$ is the context embedding for input $x$ (last token's residual after last layer),
- $\gamma \left(y\right)$ is the unembedding vector for output $y$.

Next, to align the embedding and unembedding spaces and make the Euclidean inner product a causal one (see the paper for details), a transformation using the covariance matrix of the unembedding vectors is applied:

$$g\left(y\right)=\text{Cov}\left(\gamma {)}^{-1/2}\right(\gamma \left(y\right)-E\left[\gamma \right])$$

where $\gamma$ is the unembedding vector, $E\left[\gamma \right]$ is the expected unembedding vector, and $\text{Cov}$ is the covariance matrix of $\gamma$.

Now, for any concept $W$, its vector representation ${\ell }_W$ is defined to be:

$${\overline{\ell }}_w=\left({\tilde{g}}_w^{\top }E\right(g_w\left)\right){\tilde{g}}_w,\text{where}{\tilde{g}}_w=\frac{\text{Cov}\left(g_w{)}^{†}E\right(g_w)}{\parallel \text{Cov}\left(g_w{)}^{†}E\right(g_w){\parallel }_2}$$

Given such a vector representation $l_w$ for binary concepts (where ${\ell }_{w_1}-{\ell }_{w_0}$ is the linear representation of $w_0\Rightarrow w_1$), the following orthogonality relations hold:

• ${\ell }_w\perp ({\ell }_z-{\ell }_w)\text{for}z\prec w$

  I'm skipping some notation here, but this says that for hierarchical concepts mammal $\prec$ animal, we have ${\ell }_{animal}\perp ({\ell }_{mammal}-{\ell }_{animal})$.

• ${\ell }_w\perp ({\ell }_{z_1}-{\ell }_{z_0})\text{for}\{z_0,z_1\}\prec w$

  Similarly, this means ${\ell }_{animal}\perp ({\ell }_{mammal}-{\ell }_{reptile})$.

• $({\ell }_{w_1}-{\ell }_{w_0})\perp ({\ell }_{z_1}-{\ell }_{z_0})\text{for}\{z_0,z_1\}\prec \{w_0,w_1\}$
• $({\ell }_{w_1}-{\ell }_{w_0})\perp ({\ell }_{w_2}-{\ell }_{w_1})\text{for}{w}_2\prec w_1\prec w_0$

Also, they show that categorical concepts form simplices in the transformed representation space. For each of these theorems, they give concrete proofs and provide experimental evidence on GPT-4 generated data and Gemma representations for animal categories and plants. They start with a dataset that looks like:

animals = {
    "mammal": ["beaver", "panther", "lion", "llama", "colobus", ... ], 
    "bird": ["wigeon", "parrot", "albatross", "cockatoo", "magpie", ... ], 
    "fish": ["snapper", "anchovy", "moonfish", "herring", ... ], 
    "amphibian": ["bullfrog", "siren", "toad", "treefrog", ...], 
    "insect": ["mayfly", "grasshopper", "bedbug", "silverfish", ...]
	}

Ablations

To study concepts that do not form such semantic categories and hierarchies, we add the following two datasets and play around with their codebase:

First, an "emotions" dictionary for various kinds of emotions split in various top-level emotions. Note that these categories are not expected to be orthogonal (for instance, joy and sadness should be anti-correlated). We create this via a simple call to ChatGPT.

emotions = {
   'joy': ['mirth', 'thrill', 'bliss', 'relief', 'admiration', ...],
   'sadness': ['dejection', 'anguish', 'nostalgia', 'melancholy', ...],
   'anger': ['displeasure', 'spite', 'irritation', 'disdain', ...],
   'fear': ['nervousness', 'paranoia', 'discomfort', 'helplessness', ...],
   'surprise': ['enthrallment', 'unexpectedness', 'revitalization', ...],
   'disgust': ['detestation', 'displeasure', 'prudishness', 'disdain', ...]
	}

Next, we add a "nonsense" dataset that has five completely random categories where each category is defined by a lot (order of 100) of totally random words completely unrelated to the top-level categories. This will help us get directions for random nonsensical concepts (again, via a ChatGPT call):

nonsense = {
   "random 1": ["toaster", "penguin", "jelly", "cactus", "submarine", ...],
   "random 2": ["sandwich", "yo-yo", "plank", "rainbow", "monocle", ...],
   "random 3": ["kiwi", "tornado", "chopstick", "helicopter", "sunflower", ...],
   "random 4": ["ocean", "microscope", "tiger", "pasta", "umbrella", ...],
   "random 5": ["banjo", "skyscraper", "avocado", "sphinx", "teacup", ...]
}

Hierarchical features are orthogonal - but so are semantic opposites!?

Now, let's look at their main experimental results (for animals):

And this is what we get for emotions:

While this seems okay, look at the following plot where we just look at joy and sadness in the span of sadness and all emotions:

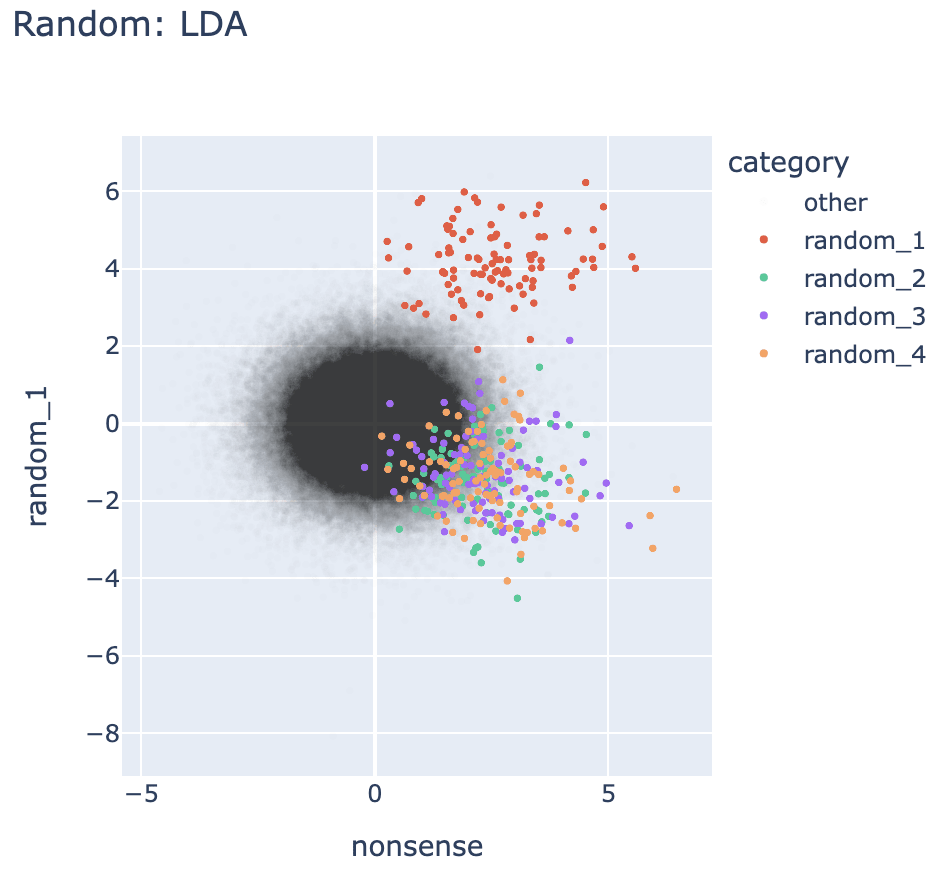
Sadness and joy are semantic opposites, so one should expect the vectors to be anti-correlated rather than orthogonal. Also, here's the same plot but for completely random, non-sensical concepts:

It seems like their orthogonality results, while true for hierarchical concepts, are also true for semantically opposite concepts and totally random concepts. 🤔

Categorical features form simplices - but so do totally random ones!?

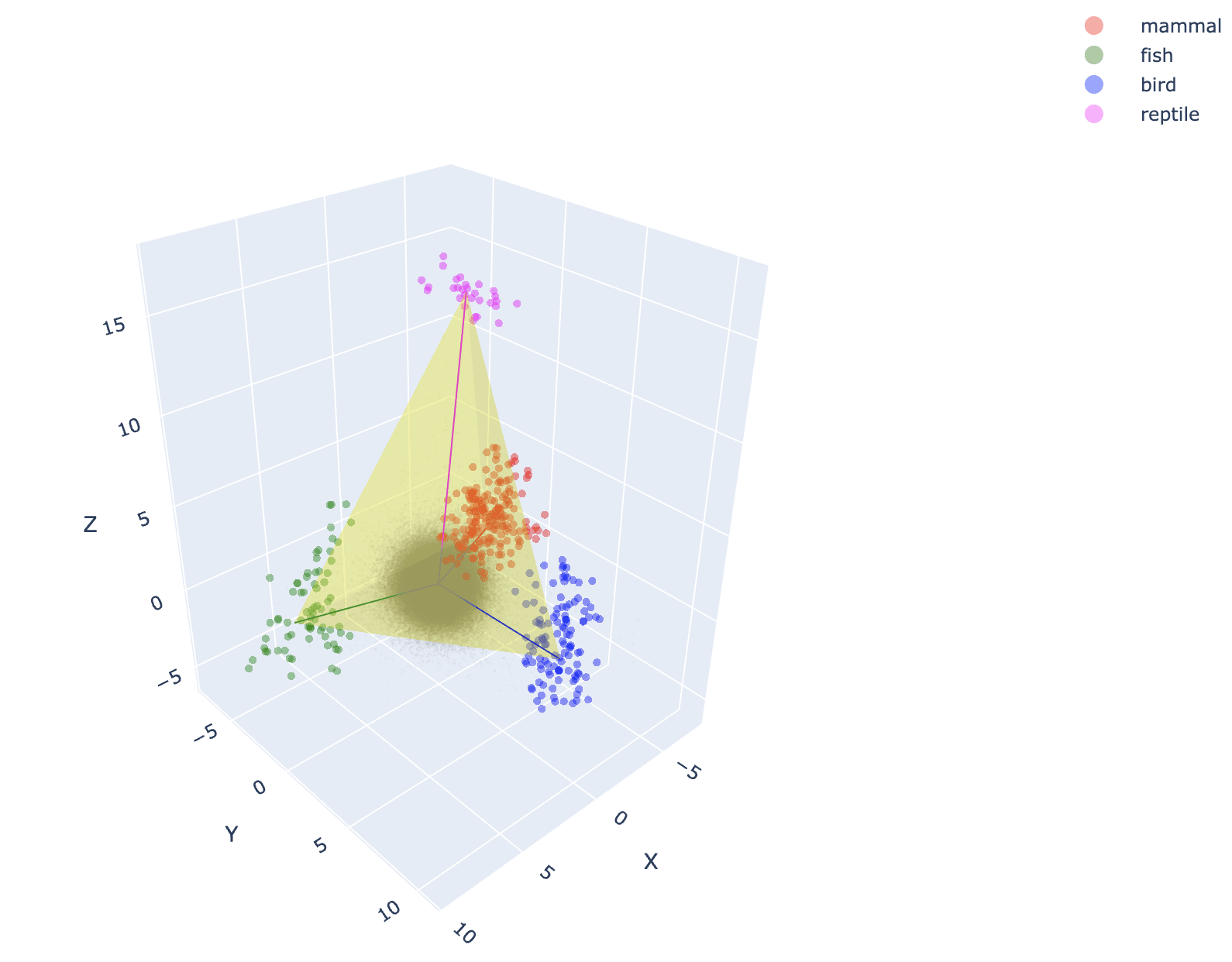
Here is the simplex they find animal categories to form:

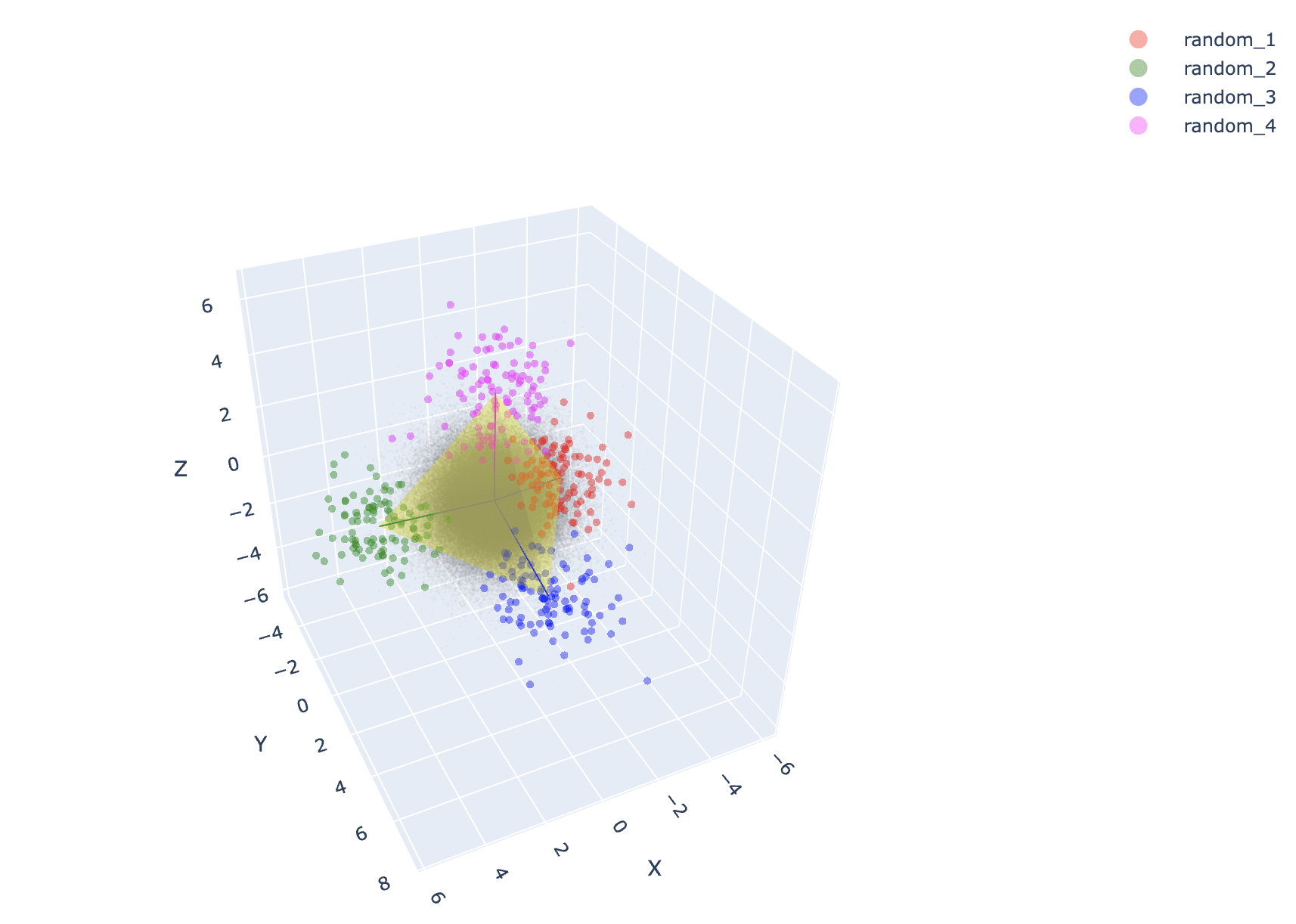
And this is what we get for completely random concepts:

Thus, while categorical concepts form simplices, so do completely random, non-sensical concepts.

Orthogonality being ubiquitous in high dimensions

Because a model's representation space is quite high-dimensional ($2048$ in the case of Gemma), and $k$ independent random vectors are expected to be almost orthogonal in  high-dimensional spaces. Multiple concrete proofs of the same are given here, but here's a quick intuitive sketch:

Let $v_1,v_2,\dots ,v_k$ be $k$ random vectors in $R^n$ with their components distributed independently and uniformly on the unit sphere. The inner product between two vectors $v_i$ and $v_j$ is given by:

$$⟨v_i,v_j⟩=\sum _{l=1}^n{v}_{i,l}{v}_{j,l}$$

and has the following variance:

$$\text{Var}[⟨v_i,v_j⟩]=\frac{1}{n}$$

Thus, as $n$ (the number of dimensions) increases, the variance tends to zero:

$$\underset{n\to \infty }{lim}\text{Var}[⟨v_i,v_j⟩]=0$$

This implies that, in high dimensions, random vectors are almost orthogonal with high probability:

$$⟨v_i,v_j⟩\approx 0\text{for}i\ne j$$
 

Discussion and Future Work

A transformation where opposite concepts seem orthogonal doesn't seem good for studying models. It breaks our semantic model of associating directions with concepts and makes steering both ways impossible.

As for categorical features forming simplices in the representation space, this claim isn't surprising because every single thing seems to form simplices, even totally random concepts.

There are lots of ways of assigning a direction or a vector to a given concept or datapoint, and it is unclear if the vectors thus obtained are correct or uniquely identifiable.

Here are some of the questions this leaves us with and ones that we'd be very excited to work on in the near future (contact us to collaborate!):

• A framework on how to think about representations that unifies how they're obtained (contrastive activations, PCA, SAE, etc.), how they're used (by the model), and how they can be used to control (eg. via steering vectors).
• How to figure out how well a given object (a direction, a vector, or even a black-box function over model parameters) represents a given human-interpretable concept or feature.
• If orthogonality and simplices are too universal and not specific enough to study the geometry of categorical and hierarchical concepts, then what is a good lens or theory to do so?