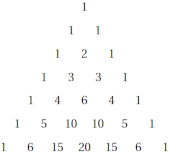Crossposting a riddle from Twitter:
Karl Marx writes in 1859 on currency debasement and inflation:
One finds a number of occasions in the history of the debasement of currency by English and French governments when the rise in prices was not proportionate to the debasement of the silver coins. The reason was simply that the increase in the volume of currency was not proportional to its debasement; in other words, if the exchange-value of commodities was in future to be evaluated in terms of the lower standard of value and to be realised in coins corresponding to this lower standard, then an inadequate number of coins with lower metal content had been issued. This is the solution of the difficulty which was not resolved by the controversy between Locke and Lowndes. The rate at which a token of value – whether it consists of paper or bogus gold and silver is quite irrelevant – can take the place of definite quantities of gold and silver calculated according to the mint-price depends on the number of tokens in circulation and by no means on the material of which they are made. The difficulty in grasping this relation is due to the fact that the two functions of money – as a standard of value and a medium of circulation – are governed not only by conflicting laws, but by laws which appear to be at variance with the antithetical features of the two functions. As regards its function as a standard of value, when money serves solely as money of account and gold merely as nominal gold, it is the physical material used which is the crucial factor. [ . . . ] [W]hen it functions as a medium of circulation, when money is not just imaginary but must be present as a real thing side by side with other commodities, its material is irrelevant and its quantity becomes the crucial factor. Although whether it is a pound of gold, of silver or of copper is decisive for the standard measure, mere number makes the coin an adequate embodiment of any of these standard measures, quite irrespective of its own material. But it is at variance with common sense that in the case of purely imaginary money everything should depend on the physical substance, whereas in the case of the corporeal coin everything should depend on a numerical relation that is nominal.
This paradox has an explanation, which resolves everything such that it stops feeling unnatural and in fact feels neatly inevitable in retrospect. I'll post it as soon as I have a paycheck to "tell the time by" again.
Until then, I'm curious whether anyone* can give the answer.
*who hasn't already heard it from me on a Discord call - this isn't very many people and I expect none of them are commenters here
"The antithesis is not so heterodox as it sounds, for every active mind will form opinions without direct evidence, else the evidence too often would never be collected."
I already know, upon reading this sentence [source] that I'm going to be quoting it constantly.
It's too perfect a rebuttal to the daily-experienced circumstance of people imagining that things - ideas, facts, heuristics, truisms - that are obvious to the people they consider politically "normal" [e.g., 2024 politically-cosmopolitan Americans, or LessWrong], must be or have been obvious to everyone of their cognitive intelligence level, at all times and in all places -
- or the converse, that what seems obvious to the people they consider politically "normal", must be true.
Separately from how pithy it is, regarding the substance of the quote: it strikes me hard that of all people remembered by history who could have said this, the one who did was R.A. Fisher. You know, the original "frequentist"? I'd associated his having originated the now-endemic tic of "testing for statistical significance" with a kind of bureaucratic indifference to unfamiliar, "fringe" ideas, which I'd assumed he'd shared.
But the meditation surrounding this quote is a paean to the mental process of "asking after the actual causes of things, without assuming that the true answers are necessarily contained within your current mental framework".
"That Charles Darwin accepted the fusion or blending theory of inheritance, just as all men accept many of the undisputed beliefs of their time, is universally admitted. [ . . . ] To modern readers [the argument from the variability within domestic species] will seem a very strange argument with which to introduce the case for Natural Selection [ . . . ] It should be remembered that, at the time of the essays, Darwin had little direct evidence on [the] point [of whether variation existed within species] [ . . . ] The antithesis is not so heterodox as it sounds, for every active mind will form opinions without direct evidence, else the evidence too often would never be collected."
This comes on the heels of me finding out that Jakob Bernoulli, the ostensible great-granddaddy of the frequentists, believed himself to be using frequencies to study probabilities, and was only cast in the light of history as having discovered that probabilities really "were" frequencies.
"This result [Jakob Bernoulli's discovery of the Law of Large Numbers in population statistics] can be viewed as a justification of the frequentist definition of probability: 'proportion of times a given event happens'. Bernoulli saw it differently: it provided a theoretical justification for using proportions in experiments to deduce the underlying probabilities. This is close to the modern axiomatic view of probability theory." [ Ian Stewart, Do Dice Play God, pg 34 ]
Bernoulli:
"Both [the] novelty [ of the Law of Large Numbers ] and its great utility combined with its equally great difficulty can add to the weight and value of all the other chapters of this theory. But before I convey its solution, let me remove a few objections that certain learned men have raised. 1. They object first that the ratio of tokens is different from the ratio of diseases or changes in the air: the former have a determinate number, the latter an indeterminate and varying one. I reply to this that both are posited to be equally uncertain and indeterminate with respect to our knowledge. On the other hand, that either is indeterminate in itself and with respect to its nature can no more be conceived by us than it can be conceived that the same thing at the same time is both created and not created by the Author of nature: for whatever God has done, God has, by that very deed, also determined at the same time." [ Jakob Bernoulli's "The Art of Conjecturing", translated by Edith Dudley Sylla ]
It makes me wonder how many great names modern "frequentism" can even accurately count among its endorsers.
Edit:
Fisher on the philosophy of probability [ PLEASE click through, it's kind of a take-your-breath-away read if you're familiar with the modern use of "p-values" ]:
"Now suppose there were knowledge a priori of the distribution of μ. Then the method of Bayes would give a probability statement, probably a different one. This would supersede the fiducial value, for a very simple reason. If there were knowledge a priori, the fiducial method of reasoning would be clearly erroneous because it would have ignored some of the data. I need give no stronger reason than that. Therefore, the first condition [of employing the frequentist definition of probability] is that there should be no knowledge a priori.
[T]here is quite a lot of continental influence in favor of regarding probability theory as a self-supporting branch of mathematics, and treating it in the traditionally abstract and, I think, fruitless way [ . . . ] Certainly there is grave confusion of thought. We are quite in danger of sending highly-trained and highly intelligent young men out into the world with tables of erroneous numbers under their arms, and with a dense fog in the place where their brains ought to be. In this century, of course, they will be working on guided missiles and advising the medical profession on the control of disease, and there is no limit to the extent to which they could impede every sort of national effort."
[ R.A. Fisher, 1957 ]
[ crossposted from my blog ]
Kolmogorov doesn't think we need "entropy".
Set physical "entropy" aside for the moment.
Here are two mutually incompatible definitions of information-theoretic "entropy".
[ Wikipedia quantifies the entropy as "average expected uncertainty" on a random variable with a distribution of possible values of arbitrary cardinality and assumes the underlying probability distribution is fixed, while Soares pins the cardinality of the distribution of possible values to 2 and assumes the probability distribution is a free variable. ]
Both these definitions are ever known as "Shannon entropy".
Kolmogorov, however, would have classed Soares's definition as, instead, a combinatorial definition of information, with the stuff about probability and entropy being parasemantic,
and dispensed entirely with Wikipedia's notion of probabilistic "entropy":
I was talking with some people yesterday whom I accused of competing to espouse middling p(doom)s. One of them was talking about Aaronson's Faust parameter [ i.e. the p(doom), assuming "everything goes perfect" if ¬doom, at which you press the button and release superintelligent AI right now ]. And they had what I think was a good question: In what year do we foresee longevity escape velocity, assuming the AInotkilleveryoneist agenda succeeds and superintelligence is forestalled for decades?
The appropriate countervailing challenge question is: What is one plausible story for how a by-chance friendly ASI invents immortality within two years or whatever of its creation, while staying harmless to humanity? What is the tech tree, how does it traverse this tree and what are the guardrails keeping it from going off on some exciting [ what is effectively to a human ] pathology-gain-of-function tangent along the way?
I'm laboriously manually Google-translating Lorenz's Der Kumpan in der Umwelt des Vogels from 1935, since I haven't been able to find an existing English translation of the complete work and don't have reliable OCR.
Rewarding passage [ boldface mine ]:
In contrast to these individually directed eliciting schemas, the innate ones are built into a complete, species-specific functional plan from the outset, in which it is determined in advance which characteristics are essential. Therefore, it only corresponds to the principle of parsimony if as few characteristics as possible are included in the eliciting schemas. For the sea urchin Sphaerechinus, it is sufficient if its exceptionally highly specialized combined flight and defense reaction against its main enemy, the starfish Asterias, is triggered by a single, specific chemical stimulus emanating from this starfish. Such triggering of a highly motorically complex behavior adapted to a very specific biological process by a single stimulus, or at least by a series of reactions, is characteristic. One would initially expect that in higher animals, to which we must necessarily attribute a material-objective grasp of the environment based on their other behavior, the object of all instinctual behaviors would also be firmly grasped. This would be considered particularly likely where a conspecific represents the object of the action. Strangely, however, a material identity of the conspecific across multiple functional circuits cannot be demonstrated in very many cases. I believe I can offer an explanation for why the subjective identity of the conspecific as an object of various functional circuits is even less of a biological necessity than that of other instinctual objects.
Even in the highest vertebrates, an object-directed instinctual sequence of actions is often triggered by a very small selection of the stimuli emanating from its object, not by its overall material image. When several functional circuits have the same object as their object, it can happen that each of these circuits responds to entirely different stimuli emanating from the same object. The innate triggering schema of an instinctual action selects, so to speak, a small selection from the abundance of stimuli emanating from its object, to which it selectively responds, thus initiating the action. The simplicity of these innate triggering schemas of different instinctual actions can result in two of them not sharing a single stimulus data that triggers their response, even though they are directed at the same object. Normally, the species-specific object sends all stimuli belonging to both schemas together. In experiments, however, the triggering schemas, which precisely because of their great simplicity can often be triggered by artificially presenting appropriate stimulus combinations, can be triggered by two different objects, thus achieving a separation of the two functional circuits directed at one object. Conversely, for the same reasons, one object can trigger two opposing, biologically meaningful reactions only with two separate objects. This is particularly common in those instinctual actions whose object is a conspecific. For example, in various species of ducks, the mother's defensive reaction can also be triggered by the cry for help of young of different species. Other caretaking reactions, on the other hand, are highly species-specific and tied to very specific coloration and marking patterns on the head and back of the offspring. Thus, it is understandable if a mallard leading her young courageously rescues a Turk's chick calling for help from danger and, in the next moment, due to the lack of the mallard-specific head and back markings that trigger further care, "unspecifically fusses" at it, i.e., attacks and kills it as a "foreign animal near its own chicks."
Today I learned: [ brook, on the EA Forum, in 2023 ], independently [?] referred to sexual selection as one of the few available examples of mesa-optimization. Before writing [ this extensive treatment of the topic in 2024 ], I don't remember seeing anyone make the connection.
I searched "sexual selection" on LessWrong for other prior examples. In 2021 Oliver Sourbut said
I think examples of sexual selection are adjacent but don't qualify as gradient hacking
This search was also my first sight of the term "Fisherian runaway"; I think Fisher, like Darwin, had too narrow a concept of the spread of traits sexual selection ultimately controls, and Fisher's influence was probably part of why Sourbut said that.
[ Ryan Kidd, 2022 ] IMO falls prey to this, but still decides that narrow examples of "Fisherian runaway" are mesa-optimizers [!].
[ lemonhope, in 2023 ], says
creatures can do sexual selection on each other instead of just getting random mutations
which pretty well encapsulates the force I think is actually driving a large percentage of modern evolution.
Other references [ none of which I'd been aware of before today ]:
Geoffrey Miller lays out the case in The Mating Mind that human creative intelligence, art, morality, and storytelling, all evolved under the pressure of sexual selection
[ Eliezer Yudkowsky in 2008 ]:
The chimp-level task of modeling others, in the hominid line, led to improved self-modeling which supported recursion which enabled language which birthed politics that increased the selection pressure for outwitting which led to sexual selection on wittiness...
...or something. It's hard to tell by looking at the fossil record what happened in what order and why. [ ambiguous; I include it mostly because I saw it referenced elsewhere while searching ]
[ Also Eliezer Yudkowsky in 2008 ]:
In the case of hominids in particular over the last few million years, we may also have been experiencing accelerated selection on brain proteins, per se - which I would attribute to sexual selection, or brain variance accounting for a greater proportion of total fitness variance. [ ? last part is a confusing-to-me ambiguation ]
[ rogersbacon, 2023 ] has some comments on sexual selection which I think are just straight up backward:
For Charles Taylor, the first Axial Age resulted from the “great disembedding” of the person from isolated communities and their natural environment, where circumscribed awareness had been limited to the sustenance and survival of the tribe guided by oral narrative myth. The lifting out from a closed-off world, according to Taylor, was enabled by the arrival of written language — the stored memories of the first cloud technology. [ -- Nathan Gardels ]
There is an analogy to biological evolution that may be instructive. When all reproduction was asexual, gene variants/mutations were “embedded” in the genome in which they arose, and their spread depended largely on the fitness of their “host genome” (vertical/clonal reproduction). With the arrival of sexual reproduction and recombination roughly two billion years ago, genes could now free themselves from their native soil and spread (horizontally) to new genomic lands. Sexual reproduction also brought a new form of selection—sexual selection—that depended less on the physical environment and more on the composition of the gene pool.
But sexual selection means the gene is more constrained, more "embedded", not less, than it was under natural selection.
It may be a broader effect of media technology & ecosystem changes: https://gwern.net/note/fashion#lorenz-spreen-et-al-2019
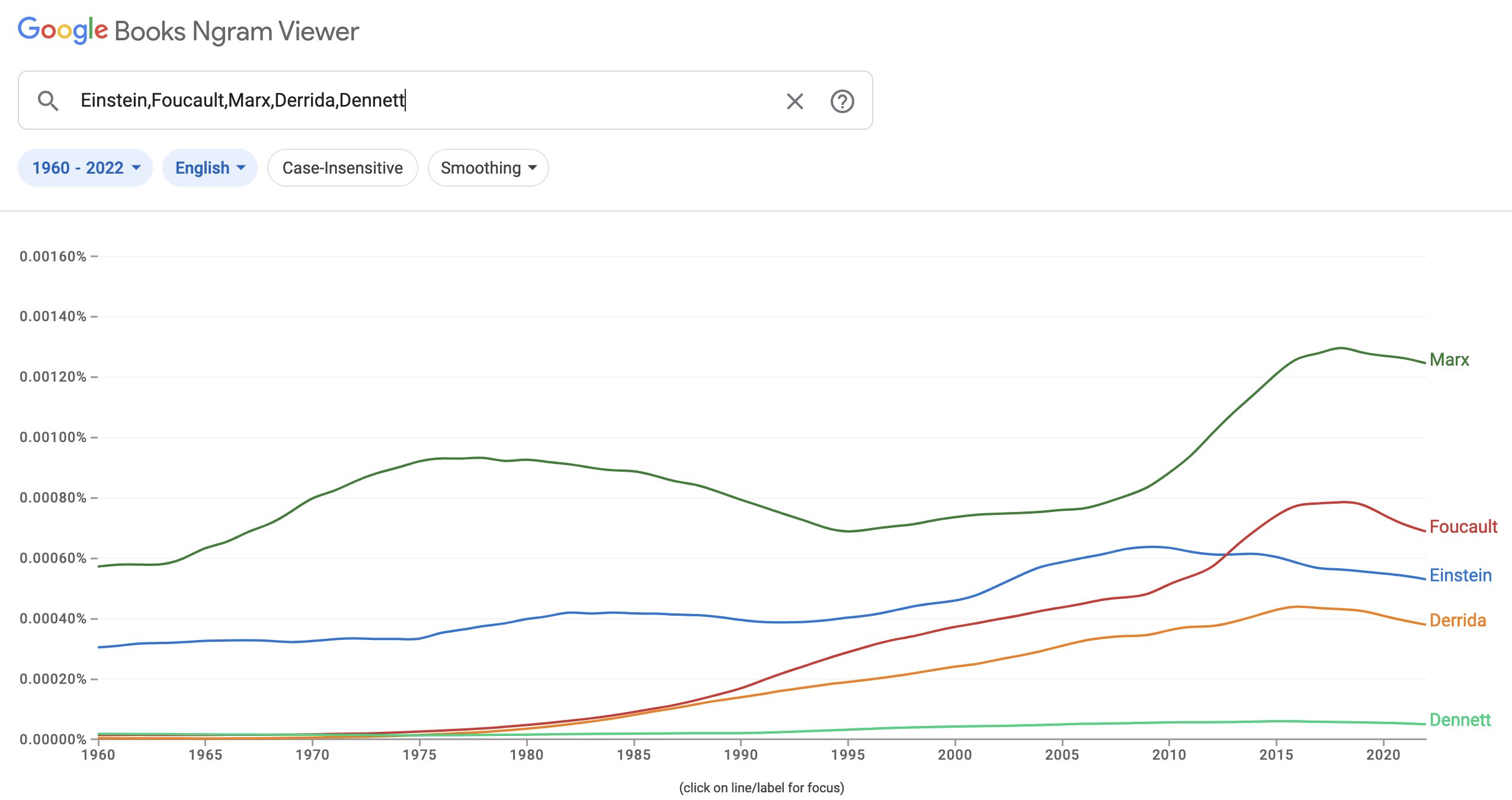
The really interesting question is, while you would generally expect old eminent figures to gradually decay (how often do you really need to cite Boethius these days?) and so I'm not surprised if you can find old eminent figures who are now in decline, are they being replaced by new major figures in an updated canon and eg. Ibram X. Kendi smoothly usurps Foucault, or just sorta... not being replaced at all and citations chaotically swirling in fashions?
I've speculated that the effect of hyper-speed media like social media is to destroy the multi-level filtering of society, and the different niches wind up separating and becoming self-contained hermetic ecosystems. (Have you ever used a powerful stand mixer to mix batter and set it too high? What happens? Well, if the contents aren't liquid enough to flow completely at high speed, you tend to observe that your contents separate, and shear off into two or three different layers, rotating inside each other, with the inner layer spinning ultra-rapidly while the outer layer possibly becoming completely static and stuck to the sides of the mixing bowl. The inner layer is Tiktok, and the stuck outer layer is places like academia. The big fads and discoveries and trends in Tiktok spin around so rapidly and are forgotten so quickly that none of them ever 'make it out' to elsewhere.)
I expect any tests to show unambiguously that it's "not being replaced at all and citations[/mentions] chaotically swirling". If I understand Evans correctly, these were all random eminent figures he picked, not selected to be falling out of fashion - and they do seem to be a pretty broad sample of the "old prestigious standard names" space.
The stand mixer is a clever analogy; I didn't previously have experience with the separation thing.
I presume you've seen Is Clickbait Destroying Our General Intelligence?, and probably Hanson's cultural evolution / cultural drift frame. I wonder if you're familiar with Callard's Distant Signals paradigm [ transcript available on episode page ], which I think is the most illuminating of the three.
Besides just the cost of ~instantaneous ~omnicast communication dropping to ~zero, I see a role for the fall of the gold standard in all this. See e.g. U.S. per capita energy usage since ~1970, international fertility since ~1970. My theory [ which I really need to make a more legible graphic for ] is that when people don't "own their money" and have to track the effects of distant inflation-adjusts from the Fed, inflation volatility [ the destructive macroeconomic thing this OP on /r/badeconomics is saying couldn't possibly be happening due to the fall of the gold standard ] goes way up. Incentives in the market for ideas are ultimately material [yes, virtual status goods influence material wealth, but it also goes the other way around], so the market for materials influences the market for ideas, and vice versa, in a vicious spiral of decline. Is the theory.
I'm still interested in this question! Someone could look at the sources I discuss in my tweet and see if this is real. https://x.com/OwainEvans_UK/status/1869357399108198489
Computer science fact of the day 2: JavaScript really was mostly-written in just a few weeks by Brendan Eich on contract-commission for Netscape [ to the extent that you consider it as having been "written [as a new programming language]", and not just specced out as a collective of "funny-looking macros" for Scheme. ] It took Eich several more months to finish the SpiderMonkey parser whose core I still use every time I browse the Internet today. However, e.g. the nonprofit R5RS did not ship a parser/interpreter [ likewise with similar committee projects ], yet it's not contested that the R5RS committee "wrote a programming language".
Computer science fact of the day 3: If you do consider JavaScript a Lisp, it's [as far as I know] the only living Lisp - not just the only popular living Lisp - to implement [ [1] first-class functions, [2] a full-featured base list fold/reduce that is available to the programmer, [3] a single, internally-consistent set of macros/idioms for operating on "typed" data ]. [1] and [2] are absolutely essential if you want to actually use most of the flexibility advantage of "writing in [a] Lisp"; [3] is essential for general usability. MIT Scheme has [1] and [2] [ and [3] to any extent, as far as I can tell ], and seems generally sensible; the major problem is that it is a dead Lisp. It has no living implementations. I have spent more than a year in a Lisp Discord server that seems full of generally competent programmers; MIT Scheme's death grip on Emacs as an interpretation/development environment seems to make it a no-go even for lots of people who aren't writing big projects and don't need, e.g., functional web crawling libraries. This has caused Scheme to fall so out of favor among working programmers that there is no Scheme option on Leetcode, Codewars, or the competitive programming site Codeforces [Codewars has a Common Lisp option, but none of the rest even have a Lisp]. For people who actually want to write production code in something that amounts to a "real Lisp", JavaScript is, today, far and away their best option. [ The vexing thing being: while functionally it is the best choice, in terms of flexible syntax, it does not offer a large % of the [very real] generally-advertised benefits of using a Lisp! ]
Two physics riddles, since my last riddle has positive karma:
-
Why do we use the right-hand rule to calculate the Lorentz force, rather than using the left-hand rule?
-
Why do planetary orbits stabilize in two dimensions, rather than three dimensions [i.e. a shell] or zero [i.e. relative fixity]? [ It's clear why they don't stabilize in one dimension, at least: they would have to pass through the center of mass of the system, which the EMF usually prevents. ]
- It's an arbitrary convention. We could have equally well chosen a convention in which a left hand rule was valid. (Really a whole bunch of such conventions)
- In the Newtonian 2-point model gravity is a purely radial force and so conserves angular momentum, which means that velocity remains in one plane. If the bodies are extended objects, then you can get things like spin-orbit coupling which can lead to orbits not being perfectly planar if the rotation axes aren't aligned with the initial angular momentum axis.
If there are multiple bodies then trajectories can be and usually will be at least somewhat non-planar, though energy losses without corresponding angular momentum losses can drive a system toward a more planar state.
Zero dimensions would only be possible if both the net force and initial velocity were zero, which can't happen if gravity is the only applicable force and there are two distinct points.
In general relativity gravity isn't really a force and isn't always radial, and orbits need not always be planar and usually aren't closed curves anyway. Though again, many systems will tend to approach a more planar state.
- Whichever coordinate system we choose, the charge will keep flowing in the same "arbitrary" direction, relative to the magnetic field. This is the conundrum we seek to explain; why does it not go the other way? What is so special about this way?
- If I'm a negligibly small body, gravitating toward a ~stationary larger body, capture in a ~stable orbit subtracts exactly one dimension from my available "linear velocity", in the sense that, maybe the other two components are fixed [over a certain period] now, but exactly one component must go to zero.
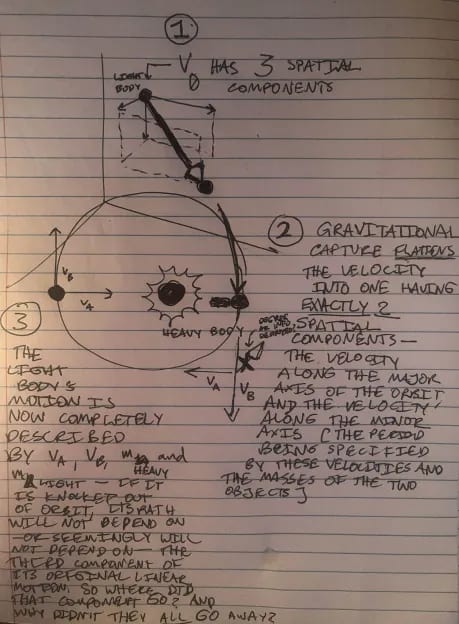
Ptolemaically, this looks like the ~stationary larger body, dragging the rest of spacetime with it in a 2-D fixed velocity [that is, fixed over the orbit's period] around me - with exactly one dimension, the one we see as ~Polaris vs ~anti-Polaris, fixed in place, relative to the me/larger-body system. That is, the universe begins rotating around me cylindrically. The major diameter and minor diameter of the cylinder are dependent on the linear velocity I entered at [ adding in my mass and the mass of the heavy body, you get the period ] - but, assuming the larger body is stationary, nothing else about my fate in the capturing orbit appears dependent on anything else about my previous history - the rest is ~erased - even though generally-relative spacetime doesn't seem to preclude more, or fewer, dependencies surviving. My question is, why is this? Why don't more, or fewer, dependencies on my past momenta ["angular" or otherwise] survive?
[ TBC, I know orbits can oscillate. However, most 3D shell orbits do not look like oscillating, but locally stable, 2D orbits. ]
While writing a recent post, I had to decide whether to mention that Nicolaus Bernoulli had written his letter posing the St. Petersburg problem specifically to Pierre Raymond de Montmort, given that my audience and I probably have no other shared semantic anchor for Pierre's existence, and he doesn't visibly appear elsewhere in the story.
I decided Yes. I think the idea of awarding credit to otherwise-silent muses in general is interesting.
If there is anything potentially interesting for the audience about Pierre Raymond de Montmort, you could also put a sentence or two in a footnote.
Footnote to my impending post about the history of value and utility:
After Pascal's and Fermat's work on the problem of points, and Huygens's work on expected value, the next major work on probability was Jakob Bernoulli's Ars conjectandi, written between 1684 and 1689 and published posthumously by his nephew Nicolaus Bernoulli in 1713. Ars conjectandi had 3 important contributions to probability theory:
[1] The concept that expected experience is conserved, or that probabilities must sum to 1.
Bernoulli generalized Huygens's principle of expected value in a random event as
[ where is the probability of the th outcome, and is the payout from the th outcome ]
and said that, in every case, the denominator - i.e. the probabilities of all possible events - must sum to 1, because only one thing can happen to you
[ making the expected value formula just
with normalized probabilities! ]
[2] The explicit application of strategies starting with the binomial theorem [ known to ancient mathematicians as the triangle pattern studied by Pascal
and first successfully analyzed algebraically by Newton ] to combinatorics in random games [which could be biased] - resulting in e.g. [ the formula for the number of ways to choose k items of equivalent type, from a lineup of n [unique-identity] items ] [useful for calculating the expected distribution of outcomes in many-turn fair random games, or random games where all more-probable outcomes are modeled as being exactly twice, three times, etc. as probable as some other outcome],
written as :
[ A series of random events [a "stochastic process"] can be viewed as a zig-zaggy path moving down the triangle, with the tiers as events, [whether we just moved LEFT or RIGHT] as the discrete outcome of an event, and the numbers as the relative probability density of our current score, or count of preferred events.
When we calculate , we're calculating one of those relative probability densities. We're thinking of as our total long-run number of events, and as our target score, or count of preferred events.
We calculate by first "weighting in" all possible orderings of , by taking , and then by "factoring out" all possible orderings of ways to achieve our chosen W condition [since we always take the same count of W-type outcomes as interchangeable], and "factoring out" all possible orderings of our chosen L condition [since we're indifferent between those too].
[My explanation here has no particular relation to how Bernoulli reasoned through this.] ]
Bernoulli did not stop with and discrete probability analysis, however; he went on to analyze probabilities [in games with discrete outcomes] as real-valued, resulting in the Bernoulli probability distribution.
[3] The empirical "Law of Large Numbers", which says that, after you repeat a random game for many turns and add up all the outcomes, the total final outcome will approach the number of turns, times the expected distribution of outcomes in a single turn. E.g. if a die is biased to roll
a 6 40% of the time
a 5 25% of the time
a 4 20% of the time
a 3 8% of the time
a 2 4% of the time, and
a 1 3% of the time
then after 1,000 rolls, your counts should be "close" to
6: .4*1,000 = 400
5: .25*1,000 = 250
4: .2*1,000 = 200
3: .08*1,000 = 80
2: .04*1,000 = 40
1: .03*1,000 = 30
and even "closer" to these ideal ratios after 1,000,000 rolls
- which Bernoulli brought up in the fourth and final section of the book, in the context of analyzing sociological data and policymaking.
One source: "Do Dice Play God?" by Ian Stewart
[ Please DM me if you would like the author of this post to explain this stuff better. I don't have much idea how clear I am being to a LessWrong audience! ]
I think, in retrospect, the view that abstract statements about shared non-reductionist reality can be objectively sound-valid-and-therefore true follows pretty naturally from combining the common-on-LessWrong view that logical or abstract physical theories can make sound-valid-and-therefore-true abstract conclusions about Reality, with the view, also common on LessWrong, that we make a lot of decisions by modeling other people as copies of ourselves, instead of as entities primarily obeying reductionist physics.
It's just that, despite the fact that all the pieces are there, it goes on being a not-obvious way to think, if for years and years you've heard about how we can only have objective theories if we can do experiments that are "in the territory" in the sense that they are outside of anyone's map. [ Contrast with celebrity examples of "shared thought experiments" from which many people drew similar conclusions because they took place in a shared map - Singer's Drowning Child, the Trolley Problem, Rawls's Veil of Ignorance, Zeno's story about Achilles and the Tortoise, Pascal's Wager, Newcomb's Problem, Parfit's Hitchhiker, the St. Petersburg paradox, etc. ]
I cannot imagine any good reason for the new UI and am immensely disappointed the siterunners are not reverting it. Technical discussion forums should not center random blobs and chic blank pages. That is destructive of their purpose. They should center the text written by their users.
Props to [ Algon ], [ Xela ], [ the gears to ascension ], and [ Zack M. Davis ]. I agree with all of them.
Not replying to the post those comments are replying to because OP is the designer, seems unfamiliar with the community, and is not responsible for any long-term effects of the changes.
Wild ahead-of-of-time guess: the true theory of gravity explaining why galaxies appear to rotate too slowly for a square root force law will also uniquely explain the maximum observed size of celestial bodies, the flatness of orbits, and the shape of galaxies.
Epistemic status: I don't really have any idea how to do this, but here I am.
Recently, Raginrayguns and Philosophy Bear both [presumably] read "Cargo Cult Science" [not necessarily for the first time] on /r/slatestarcodex. I follow both of them, so I looked into it. And TIL that's where "cargo-culting" comes from. He doesn't say why it's wrong, he just waves his hands and says it doesn't work and it's silly. Well, now I feel silly. I've been cargo-culting "cargo-culting". I'm a logical decision theorist. Cargo cults work. If they work unreliably, so do reductionistic methods.