LESSWRONG
LW

Comment Permalink

Maybe the bias comes from the perception that the unknown risk has to be either very low or very large. It would make sense, for example, for low risks such as getting hit by a lightning.

Let us suppose that I am willing to tolerate a certain maximum risk, say <1%.

I do not know the real risk of interacting with people, but I want that Nx < 0.01 (if linear), where N is the number of contacts and x is the unknown risk per contact.

Now, if I am already willing to meet 99 people, this means that I am guessing x < 0.01 / 99.

I would accept to increase to 100 if x < 0.01 /100. Not wanting to meet 100 people when you already meet 99 means estimating that

0.01 /100 < x < 0.01 / 99

which would be a weirdly precise claim to make.

On the other hand, if I am wrong in estimating x < 0.01 / 99, it may be that x>0.1, for example, and then we are outside the linear regime, and the risk of 99 is very similar to the risk of 100 (as they are both close to 1).

Of course this heuristic fails if the unknown risk is in at intermediate scale probability, neither evident neither extremely low (like in the case of covid).

See in context

84 Quadratic, not logarithmic

by Valentin2026

8th Feb 2021

1 min read

84

I recently realized a very simple, almost obvious bias, that I had because I never thought more about it. Moreover, quite a lot of people have this bias too.

What is worse in time of pandemic - to increase the number of your contacts from 0 to 1 or from 99 to 100? Intuitively, since we perceive many quantities on a logarithmic scale, the first thing is much worse. I heard multiple times something like: "I am already doing this and this and that because I have to, so it does not make sense for me to decrease my shopping", or "My roommate (spouse, child...) does not care about this at all, so it does not make sense for me either".

However, this is simply not true. If I care solely about myself, increasing the number of contacts increases the probability to get sick linearly - no logarithmic scale. But if I also care about other people (my contacts, yes), then we have linear growth of probability to become a spreader, and linear growth of the group to whom I can spread, thus leading to quadratic growth of the total expected damage to society.

So, if I have quite a lot of contacts already, I should be much more cautious about adding more than if I have almost none. It sounds so trivial right now - yet so many times I have heard the opposite advice.

Covid-19Rationality

Frontpage

84

New Comment

23 comments, sorted by

top scoring

Click to highlight new comments since: Today at 2:20 AM

[-]Kaj_Sotala4y200

To rephrase what I took to be the essential gist: if you go from meeting 0 people to meeting 1 person, you are only exposing yourself to (some) additional risk. But if you are regularly seeing 99 people, then by adding on a hundredth person, you are now exposing all of those 99 to potentially getting infected from the hundredth.

Thus going from 99 to 100 is worse than going from 0 to 1, since 0 -> 1 exposes no people other than yourself to added risk, whereas 99 -> 100 exposes 99 other people than yourself to added risk.

[-]MrThink4y70

Maybe I misunderstood something, but is really the odds of getting sick yourself growing linearly?

Let's say if you meet 1 person the odds of getting corona is 1%. That would mean that meeting 101 people would result in a 101% chance in getting corona. Sure, it is almost linear until you get to about 10 people (in my example), but the curve of risk to get corona should follow something like 1-(0.99)^n if we assume the risk of getting corona is equal from every person you have contact with.

Spreading it linearly with the number of people you meet however I can understand the reasoning behind.

[-]TheMajor4y90

You are correct, but the hope is that the probabilities involved stay low enough that a linear approximation is reasonable. Using for example https://www.microcovid.org/, typical events like a shopping trip carry infection risks well below 1% (dependent on location, duration of activity and precautions etc.).

[-]hamnox4y80

Here's that's risk curve.

and the risk-to-others curve, against the 0.01x*0.30x quadratic for reference. the risk gets closer to linear the farther out you go.

Expected contribution to spread given number of contacts
(assuming 30% transmission risk if positive)

I have no idea how to model the effects beyond this point tbqh. There's complicated probability dependence among social contacts and I don't know how to avoid double-counting people who were already infected.

Also keep the Gambler's fallacy in mind when considering whether to add contacts:
If you meet 1 person then the risk is 1%. If you meet 100 people the risk is 63%. If you meet 99 people, confirm you didn't get covid, and then meet 1 more, your risk is 1%.
(Very Approximately because, again, there's complicated probability dependence among social contacts.)

[-]ADifferentAnonymous4y30

I remember very early in the pandemic reading an interview with someone who justified their decision to continue going to bars by pointing that they had a high-contact job that they still had to do. I noticed that this in fact made their decision worse (in terms of total societal Covid risk).

(And as the number of cases was still quite low at the time, the 100% bound on risk was much less plausibly a factor)

[-]Liron4y30

A lot depends on what type of “interactions” we’re considering, and how uniform the distribution is: indoor/outdoor, masks on/off, etc. If we assume that all interactions are of the identical type, then the quadratic model is useful.

But in a realistic scenario, they’re probably not identical interactions, because the 100 interactions probably divide across different life contexts, e.g. 5 different gatherings with 20 interactions each.

Therefore, contrary to what this post seems to imply, I believe the heuristic of “I’ve already interacted with 99 people so I’m not going to go out of my way to avoid 1 more” is directionally correct in most real-life scenarios, because of the Pareto (80/20) principle.

In a realistic scenario, you can probably model the cause of your risk as having one or two dominant factors, and modeling the dominant factors probably doesn’t look different when adding one marginal interaction, unless that interaction is the disproportionally risky one compared to the others.

On the other hand, when going from 0 to 1 interactions, it’s more plausible to imagine that this 1 interaction is one of the most dominant risk factors in your life, because it has a better shot of changing your model of dominant risks.

[-]Bucky4y30

This is interesting.

Trying to think when logarithmic thinking makes sense and why humans might often think like that:

If I am in control of all (or almost all) of my risks then a pandemic where I am only taking a 0 person risk is very different from a pandemic where I am taking a 99 person risk. So moving from 0 to 1 in the presumably-very-deadly-pandemic where I am being super-cautious is a very bad thing. Moving from 99 to 100 in the probably-not-too-bad-pandemic where I'm already meeting up with 99 people is probably not too bad.

So thinking logarithmically makes sense if my base level of risk is strongly correlated to the deadliness of the pandemic. The more sensible route is to skip the step of looking at what risk I'm taking to give me evidence of how bad things are and just look directly at how bad things are.

In the 2 examples you give there are external reasons for additional base risk and these are not (strongly) correlated with the deadliness of the pandemic.

[-]ADifferentAnonymous4y50

Another explanation for logarithmic thinking is Laplace's rule of succession.

If you have N exposures and have not yet had a bad outcome, the Laplacian estimate of a bad outcome from the next exposure goes as 1/N (the marginal cost under a logarithmic rule).

Applying this to "number of contacts" rather than "number of exposures" is admittedly more strained but I could still see it playing a part.

[-]mwacksen4y20

Say you meet in a group of people that all care about each other. Then, by your reasoning, each of the $n$ people is responsible for $n^{2}$ risk, so in fact (by double counting once more as in the original post), the total risk is $n^{3}$ . If however, we share the responsibility equally each person is responsible for $n$ risk which is intuitive. So this quadratic growth assumption is a bit questionable, I'd like to see it done more formally because my intuition says it is not complete nonsense, but it's obviously not the whole truth.

I feel like this is almost too obvious to state, but question is really not about the marginal risk, but about the marginal benefit. Meeting 0 people probably is really bad your mental health in comparison to meeting 2. Meeting 98 people is probably not much worse for your mental health compared to meeting 100. Meeting 2 people might be more than twice as good as meeting one. But since we don't just care about ourselves, we should also think about the other person's benefit. So even if you are already meeting 98 people but the 99th meets nobody else the benefit you provide to that person may (depending on your age, preconditions, etc...) be worth more than the extra bit of risk.

[-]cistran4y10

You are not allowed to not care for yourself. Particularly, you should take care that you are not infected, because if you are not infected you cannot spread the virus.

[-]mwacksen4y10

Sorry for the (very) late reply, but I do not understand this comment and suspect maybe my point didn't come accross clearly, cf. also my other reply to the comment below this one.

[-]ADifferentAnonymous4y10

If you're deciding whether or not to add the (n+1)th person, what matters is the marginal risk of that decision.

[-]mwacksen4y10

Apologies for the really late reply, but I don't think "marginal risk" in this context is well-defined. The marginal risk to yourself grows linearly in the number of people to first order. You could feel responsible for the marginal risk to all the other party goers, but they are people with their own agency, you aren't (in my opinion) responsible for managing their risk.

[-]DirectedEvolution4y20

Does a simple quadratic model really work for modeling disease spread? Other factors that seem critical:

How closely connected each new person you see is to the others in your prior network of contacts
The degree to which people trade off safety precautions against additional risk
The number of people you see in the window during which you could be infectious
The fact that the kind of person who's seeing lots of other people might also be the kind of person to eschew other safety precautions
Whether or not you see these contacts every day, or whether you see a sequence of new contacts without seeing the previous people in the sequence

Before I used anything like this to try and model the effect of changing the number of contacts, I'd really want to see some more robust simulation.

Some aspects of this model seem plausible on its face. For example, a recluse who starts to see one person only puts himself at risk. If he starts seeing two people, though, he's now creating a bridge between them, putting them both at elevated risk.

[-]Raemon4yModerator Comment20

Mod note: frontpage (despite not usually frontpaging coronavirus content) because the lesson seemed somewhat generalizable.

[-]J Mann4y10

My intuition is that people get confused whether they're measuring the risk to themselves or the risk to society from their Covid decisions.

It seems like a lot of people I know have decided that they'd rather accept the increased risk of serious injury or death rather than have a substantially reduced quality of life for a year or two. Ok, fine. (Although it's hard to measure small risks.)
On the other hand, the other problem is that even if the person is accepting the risk for themselves, I'm not sure they're processing the risk that somebody else gets seriously ill or dies.

It might be that public pressure focusing on the risk to each of us is obscuring some of the risk to other people, or it might just be a collective action problem - if a mayor encourages other people to be vigilant about Covid from his beach vacation in Mexico, well, that does much less damage as long as everybody else follows his advice.

[-]mwacksen4y10

On the other hand, the other problem is that even if the person is accepting the risk for themselves, I'm not sure they're processing the risk that somebody else gets seriously ill or dies.

Well maybe, but are you thinking of the fact that (trivially) P(you infect someone else) < P(you are infected)?

[-]gjm4y20

But if infected you may infect several other people, and indirectly the number of people infected who wouldn't have been if you'd been more careful may be very large.

[-]cistran4y10

That's the point of the post. Given a large number of contacts, P(infecting at least one of them) > P(you are infected)

Lets illustrate. Suppose P1(you are infected AND (you are asymptomatic OR you are pre-symptomatic))

P2(infecting any one of your contacts) = P2'*P1 = where P2' is the probability of infection per contact

Then P3(infecting at least one of your contacts out of N) = 1- (1-P2)^N provided none of the N contacts are themselves infected.

And in P3>P1 it is always possible to solve for N.

[-]mwacksen4y10

Sorry for the late reply. I'm assuming you need to be "infected" in order to infect someone else (define "infected" so that this is true). Since being infected is a neccessary precondition to infecting someone else,

P(you infect someone else) <= P(you are infected),

and it's clear you can replace "<=" by "<".

This is basic probaility theory, I can't follow your notation but suspect that you are using some different definition of "infected" and/or confusing probabilities with expected values..

[-]J Mann4y10

I'm not good at expressing it formally, but I was thinking more:

Expected total utility to my friend of going to a bar with her granddaughters > expected total value to her of staying home,* but the the expected utility to society of her going to the bar with her grandkids is negative.
As long as enough other people stay home, on the other hand, the social costs of her going out are not as high as they would be if more people went out.
On the third hand, even if a bunch of people going out increases the cost (to both herself and society) of her going out, watching other people defect makes her feel like a sucker.

*She's in her late 70s, and my feeling is she's don't the math and figures she may not have that many good years left, so she didn't want to miss out on one, even if it increased her life expectancy.

[-]MikkW4y10

I would have found it useful if the title reflected that this is discussing COVID / infectious outbreaks. That said, I appreciated this post for pointing out an area where human intuitions are likely to misjudge the actual effects of a change in behavior, and providing a more accurate model of what the actual dynamics are (with the caveat that ViktorThink pointed out that as contacts increase, the risk of getting infected stops being linear)

[-]ForensicOceanography4y10

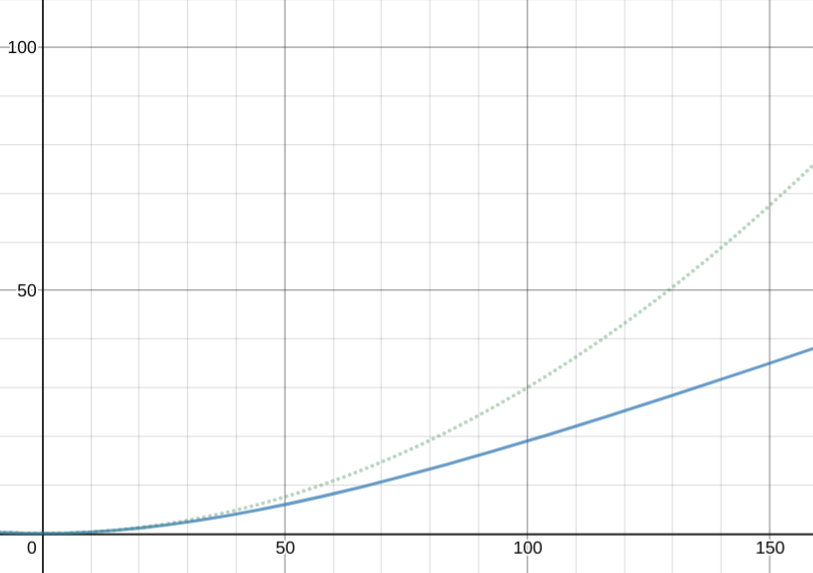
Maybe the bias comes from the perception that the unknown risk has to be either very low or very large. It would make sense, for example, for low risks such as getting hit by a lightning.

Let us suppose that I am willing to tolerate a certain maximum risk, say <1%.

I do not know the real risk of interacting with people, but I want that Nx < 0.01 (if linear), where N is the number of contacts and x is the unknown risk per contact.

Now, if I am already willing to meet 99 people, this means that I am guessing x < 0.01 / 99.

I would accept to increase to 100 if x < 0.01 /100. Not wanting to meet 100 people when you already meet 99 means estimating that

0.01 /100 < x < 0.01 / 99

which would be a weirdly precise claim to make.

Of course this heuristic fails if the unknown risk is in at intermediate scale probability, neither evident neither extremely low (like in the case of covid).

Moderation Log