Tl;dr, Neural networks are deterministic and sometimes even reversible, which causes Shannon information measures to degenerate. But information theory seems useful. How can we square this (if it's possible at all)? The attempts so far in the literature are unsatisfying.
Here is a conceptual question: what is the Right Way to think about information theoretic quantities in neural network contexts?
Example: I've been recently thinking about information bottleneck methods: given some data distribution , it tries to find features specified by that have nice properties like minimality (small ) and sufficiency (big ).
But as pointed out in the literature several times, the fact that neural networks implement a deterministic map makes these information theoretic quantities degenerate:
- if Z is a deterministic map of X and they’re both continuous, then I(X;Z) is infinite.
- Binning / Quantizing them does turn Z into a stochastic function of X but (1) this feels very adhoc, (2) this makes the estimate depend heavily on the quantization method, and (3) this conflates information theoretic stuff with geometric stuff, like clustering of features making them get quantized into the same bin thus artificially reducing MI.
- we could deal with quantized neural networks and that might get rid of the conceptual issues with infinite I(X;Z), but …
- Reversible networks are a thing. The fact that I(X;Z) stays the same throughout a constant-width bijective-activation network for most parameters - even randomly initialized ones that intuitively “throws information around blindly” - just doesn’t seem like it’s capturing the intuitive notion of shared information between X and Z (inspired by this comment).
There are attempts at solving these problems in the literature, but the solutions so far are unsatisfying: they're either very adhoc, rely on questionable assumptions, lack clear operational interpretation, introduce new problems, or seem theoretically intractable.
- (there’s the non-solution of only dealing with stochastic variants of neural networks, which is unsatisfactory since it ignores the fact that neural networks exist and work fine without stochasticity)
Treat the weight as stochastic:
This paper (also relevant) defines several notions of information measure relative to an arbitrary choice of and (not a Bayesian posterior):
- measure 1: “information in weight”
- specifically, given , choose to minimize a term that trades off expected loss under and weighted by some , and say the KL term is the information in the weights at level for .
- interpretation: additional amount of information needed to encode (relative to encoding based on prior) the weight distribution which optimally trades off accuracy and complexity (in the sense of distance from prior).
- measure 2: “effective information ” is , where is a deterministic function of parameterized by , is a stochastic function of where is perturbed by some the that minimizes the aforementioned trade off term.
- interpretation: amount of "robust information” shared between the input and feature that resists perturbation in the weights - not just any perturbation, but perturbations that (assuming is e.g., already optimized) lets the model retain a good loss / complexity tradeoff.
I like their idea of using shannon information measures to try to capture a notion of “robustly” shared information. but the attempts above so far seem pretty ad hoc and reliant on shaky assumptions. i suspect SLT would be helpful here (just read the paper and see things like casually inverting the fisher information matrix).
Use something other than shannon information measures:
There’s V-information which is a natural extension of shannon information measures when you restrict the function class to consider (due to e.g., computational constraints). But now the difficult question is the choice of natural function class. Maybe linear probes are a natural choice, but this still feels ad hoc.
There’s K-complexity, but there's the usual uncomputability and the vibes of intractability in mixing algorithmic information theory notions with neural networks when the latter has more of a statistical vibe than algorithmic. idk, this is just really vibes, but I am wary of jumping to the conclusion of thinking AIT is necessary in information theoretically analyzing neural networks based on the "there's determinism and AIT is the natural playing field for deterministic information processing systems"-type argument.
Ideally, I could keep using the vanilla shannon information measures somehow because they’re nice and simple and computable and seems potentially tractable both empirically and theoretically.
And so far, I haven't been able to find a satisfying answer to the problem. I am curious if anyone has takes on this issue.
I'm not entirely sure what you've looked at in the literature; have you seen "Direct Validation of the Information Bottleneck Principle for Deep Nets" (Elad et al.)? They use the Fenchel conjugate
\[\mathrm{KL}(P||Q) = \sup_{f} [\mathbb{E}_P[f]-\log (\mathbb{E}_Q[e^f])]\]This turns finding the KL-divergence into an optimisation problem for \(f^*(x) = \log \frac{p(x)}{q(x)}\). Since
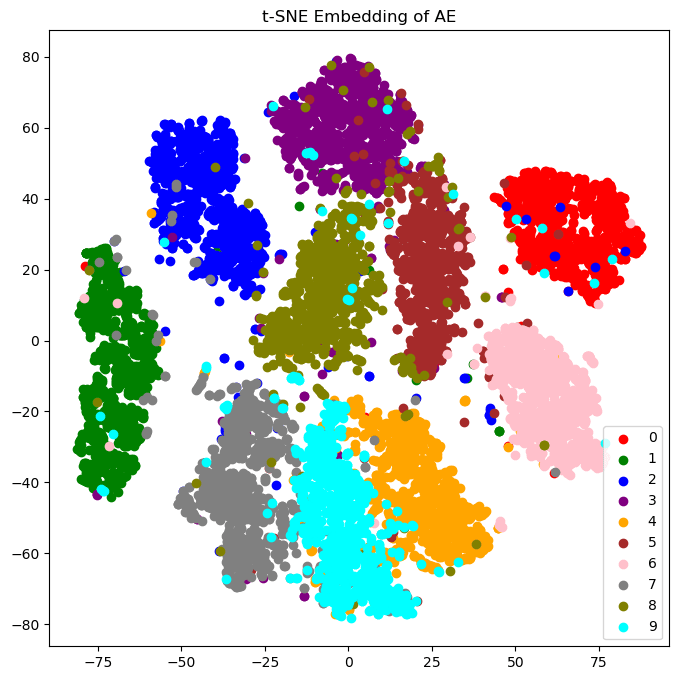
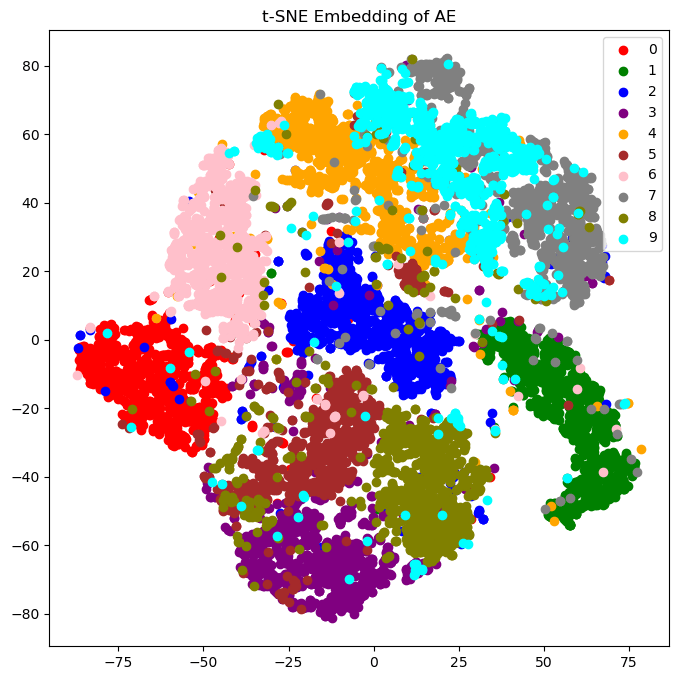
\[I(X;Y)=\mathrm{KL}(P_{X,Y}||P_{X\otimes Y}),\]you can train a neural network to predict the mutual information. For the information bottleneck, you would train two additional networks. Ideal lossy compression maximises the information bottleneck, so this can be used as regularization for autoencoders. I did this for a twenty-bit autoencoder of MNIST (code). Here are the encodings without mutual information regularization, and then with it:
Notice how the digits are more "spread out" with regularization. This is exactly the benefit variational autoencoders give, but actually based in theory! In this case, my randomness comes from the softmax choice for each bit, but you could also use continuous latents like Gaussians. In fact, you could even have a deterministic encoder, since the mutual information predictor network is adversarial, not omniscient. The encoder can fool it during training by having small updates in its weights make large updates in the latent space, which means (1) it's essentially random in the same way lava lamps are random, (2) the decoder will learn to ignore noise, and (3) the initial distribution of encoder weights will concentrate around "spines" in the loss landscape, which have lots of symmetries in all dimensions except the important features you're encoding.
The mutual information is cooperative for the decoder network, which means the decoder should be deterministic. Since mutual information is convex, i.e. if we had two decoders \(\phi_1, \phi_2: Z\to Y\), then
\[\lambda I(Z; \phi_1(Z)) + (1-\lambda) I(Z; \phi_2(Z)) \ge I(Z; (\lambda\phi_1 + (1-\lambda)\phi_2)(Z)).\]Every stochastic decoder could be written as a sum of deterministic ones, so you might as well use the best deterministic decoder. Then
\[I(Z; \phi(Z)) = H(\phi(Z)) \cancel{-H(\phi(Z)|Z)}\]so you're really just adding in the entropy of the decoded distribution. The paper "The Deterministic Information Bottleneck" (Strauss & Schwab) argues that the encoder \(\psi: X\to Z\) should also be deterministic, since maximising
\[-\beta I(X; \psi(X)) = \beta[H(\psi(X)|X) - H(\psi(X))]\]seems to reward adding noise irrelevant to \(X\). But that misses the point; you want to be overwriting unimportant features of the image with noise. It's more clear this is happening if you use the identity
\[-\beta I(X;\psi(X)) = \beta H(X|\psi(X))\cancel{ - \beta H(X)}\](the second term is constant). This is the same idea behind variational autoencoders, but they use \(\mathrm{KL}(\psi(X)||\mathcal{N}(0, 1))\) as a cheap proxy to \(H(X|\psi(X))\).