6 Answers sorted by
213
The key question is: mutual information of what, with what, given what? The quantity is I(X;Y|Z); what are X, Y, and Z? Some examples:
- Mutual information of the third and eighth token in the completion of a prompt by a certain LLM, given prompt and weights (but NOT the random numbers used to choose each token from the probability distribution output by the model for each token).
- Mutual information of two patches of the image output by an image model, given prompt and weights (but NOT the random latents which get denoised to produce the image).
- Mutual information of two particular activations inside an image net, given the prompt and weights (but NOT the random latents which get denoised).
- Mutual information of the trained net's output on two different prompts, given the prompts and training data (but NOT the weights). Calculating this one would (in principle) involve averaging over values of the trained weights across many independent training runs.
- Mutual information between the random latents and output image of an image model, given the prompt and weights. This is the thing which is trivial because the net is deterministic. All the others above are nontrivial.
Thank you, first three examples make sense and seem like an appropriate use of mutual information. I'd like to ask about the fourth example though, where you take the weights as unknown:
- What's the operational meaning of under some ? More importantly: to what kind of theoretical questions we could ask are these quantities an answer to? (I'm curious of examples in which such quantities came out as a natural answer to the research questions you were asking in practice.)
- I would guess the choice of (maybe the bayesian po
102
What application do you have in mind? If you're trying to reason about formal models without trying to completely rigorously prove things about them, then I think thinking of neural networks as stochastic systems is the way to go. Namely, you view the weights as a random variable solving a stochastic optimization problem to produce a weight-valued random variable, then conditioning it on whatever knowledge about the weights/activations you assume is available. This can be done both in the Bayesian "thermostatic" sense as a model of idealized networks, and in the sense of modeling the NN as SGD-like systems. Both methods are explored explicitly (and give different results) in suitable high width limits by the PDLT and tensor networks paradigms (the latter also looks at "true SGD" with nonnegligible step size).
Here you should be careful about what you condition on, as conditioning on exact knowledge of too much input-output behavior of course blows stuff up, and you should think of a way of coarse-graining, i.e. "choose a precision scale" :). Here my first goto would be to assume the tempered Boltzmann distribution on the loss at an appropriate choice of temperature for what you're studying.
If you're trying to do experiments, then I would suspect that a lot of the time you can just blindly throw whatever ML-ish tools you'd use in an underdetermined, "true inference" context and they'll just work (with suitable choices of hyperparameters)
I just read your koan and wow it's a great post, thank you for writing it. It also gave me some new insights as to how to think about my confusions and some answers. Here's my chain of thought:
- if I want my information theoretic quantities to not degenerate, then I need some distribution over the weights. What is the natural distribution to consider?
- Well, there's the Bayesian posterior.
- But I feel like there is a sense in which an individual neural network with its weight should be considered as a deterministic information processing system on its own, witho
30
First, I agree with Dmitry.
But it does seem like maybe you could recover a notion of information bottleneck even with out the Bayesian NN model. If you quantize real numbers to N-bit floating point numbers, there's a very real quantity which is "how many more bits do you need to exactly reconstruct X, given Z?" My suspicion is that for a fixed network, this quantity grows linearly with N (and if it's zero at 'actual infinity' for some network despite being nonzero in the limit, maybe we should ignore actual infinity).
But this isn't all that useful, it would be nicer to have an information that converges. The divergence seems a bit silly, too, because it seems silly to treat the millionth digit as as important as the first.
So suppose you don't want to perfectly reconstruct X. Instead, maybe you could say the distribution of X is made of some fixed number of bins or summands, and you want to figure out which one based on Z. Then you get a converging amount of information, and you correctly treat small numbers as less important, but you've had to introduce this somewhat arbitrary set of bins. shrug
That makes sense. I've updated towards thinking this is reasonable (albeit binning and discretization is still ad hoc) and captures something real.
We could formalize it like where with being some independent noise parameterized by \sigma. Then would become finite. We could think of binning the output of a layer to make it stochastic in a similar way.
Ideally we'd like the new measure to be finite even for deterministic maps (this is the case for above) and some strict d...
20
Another perspective would be too look at the activations of an autoregressive deep learning model, e.g. a transformer, during inference as a stochastic process: the collection of activation at some layer as random variables indexed by time t, where t is token position.
One could for example look at mutual information between the history and the future of the activations , or look at (conditional) mutual information between the past and future of subprocesses of (note: transfer entropy can be a useful tool to quantify directed information flow between different stochastic processes). There are many information-theoretic quantities one could be looking at.
If you want to formally define a probability distribution over activations, you could maybe push forward the discrete probability distribution over tokens (in particular the predictive distribution) via the embedding map.
In the context of computational mechanics this seems like a useful perspective, for example to find belief states by optimizing mutual information between some coarse graining of the past states and future states to find belief states in a data-driven way (this is too vague stated like that, and i am working on a draft that get into more details about that perspective).
10
I'm not entirely sure what you've looked at in the literature; have you seen "Direct Validation of the Information Bottleneck Principle for Deep Nets" (Elad et al.)? They use the Fenchel conjugate
\[\mathrm{KL}(P||Q) = \sup_{f} [\mathbb{E}_P[f]-\log (\mathbb{E}_Q[e^f])]\]This turns finding the KL-divergence into an optimisation problem for \(f^*(x) = \log \frac{p(x)}{q(x)}\). Since
\[I(X;Y)=\mathrm{KL}(P_{X,Y}||P_{X\otimes Y}),\]you can train a neural network to predict the mutual information. For the information bottleneck, you would train two additional networks. Ideal lossy compression maximises the information bottleneck, so this can be used as regularization for autoencoders. I did this for a twenty-bit autoencoder of MNIST (code). Here are the encodings without mutual information regularization, and then with it:
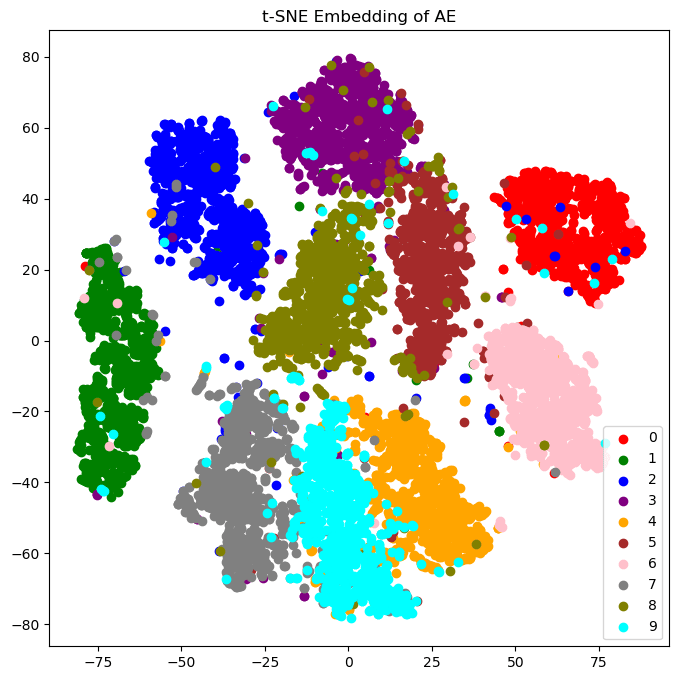
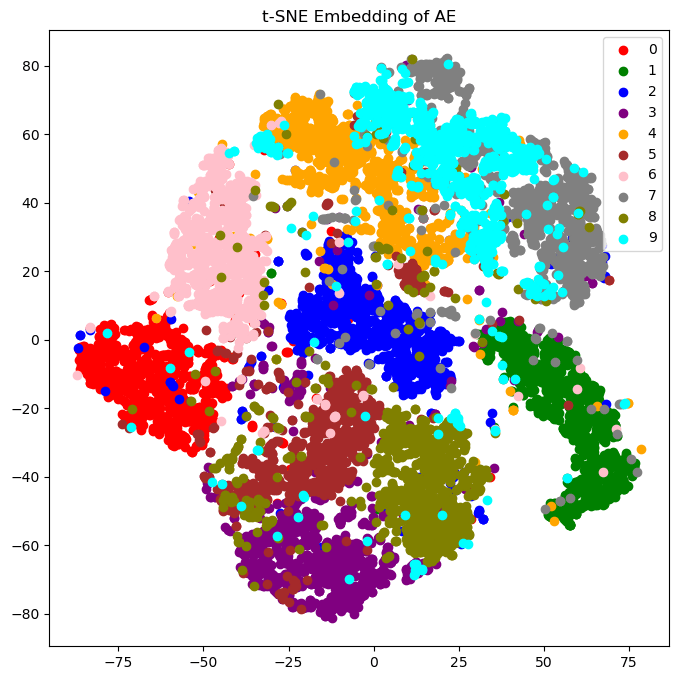
Notice how the digits are more "spread out" with regularization. This is exactly the benefit variational autoencoders give, but actually based in theory! In this case, my randomness comes from the softmax choice for each bit, but you could also use continuous latents like Gaussians. In fact, you could even have a deterministic encoder, since the mutual information predictor network is adversarial, not omniscient. The encoder can fool it during training by having small updates in its weights make large updates in the latent space, which means (1) it's essentially random in the same way lava lamps are random, (2) the decoder will learn to ignore noise, and (3) the initial distribution of encoder weights will concentrate around "spines" in the loss landscape, which have lots of symmetries in all dimensions except the important features you're encoding.
The mutual information is cooperative for the decoder network, which means the decoder should be deterministic. Since mutual information is convex, i.e. if we had two decoders \(\phi_1, \phi_2: Z\to Y\), then
\[\lambda I(Z; \phi_1(Z)) + (1-\lambda) I(Z; \phi_2(Z)) \ge I(Z; (\lambda\phi_1 + (1-\lambda)\phi_2)(Z)).\]Every stochastic decoder could be written as a sum of deterministic ones, so you might as well use the best deterministic decoder. Then
\[I(Z; \phi(Z)) = H(\phi(Z)) \cancel{-H(\phi(Z)|Z)}\]so you're really just adding in the entropy of the decoded distribution. The paper "The Deterministic Information Bottleneck" (Strauss & Schwab) argues that the encoder \(\psi: X\to Z\) should also be deterministic, since maximising
\[-\beta I(X; \psi(X)) = \beta[H(\psi(X)|X) - H(\psi(X))]\]seems to reward adding noise irrelevant to \(X\). But that misses the point; you want to be overwriting unimportant features of the image with noise. It's more clear this is happening if you use the identity
\[-\beta I(X;\psi(X)) = \beta H(X|\psi(X))\cancel{ - \beta H(X)}\](the second term is constant). This is the same idea behind variational autoencoders, but they use \(\mathrm{KL}(\psi(X)||\mathcal{N}(0, 1))\) as a cheap proxy to \(H(X|\psi(X))\).
Thanks for reminding me about V-information. I am not sure how much I like this particular definition yet - but this direction of inquiry seems very important imho.
I like the definition, it's the minimum expected code length for a distribution under constraints on the code (namely, constraints on the kind of beliefs you're allowed to have - after having that belief, the optimal code is as always the negative log prob).
Also the examples in Proposition 1 were pretty cool in that it gave new characterizations of some well-known quantities - log determinant of the covariance matrix does indeed intuitively measure the uncertainty of a random variable, but it is very cool to see that it in fact has entropy interpretations!
It's kinda sad because after a brief search it seems like none of the original authors are interested in extending this framework.
Tl;dr, Neural networks are deterministic and sometimes even reversible, which causes Shannon information measures to degenerate. But information theory seems useful. How can we square this (if it's possible at all)? The attempts so far in the literature are unsatisfying.
Here is a conceptual question: what is the Right Way to think about information theoretic quantities in neural network contexts?
Example: I've been recently thinking about information bottleneck methods: given some data distribution P(X,Y), it tries to find features Z specified by P(Z|X) that have nice properties like minimality (small I(X;Z)) and sufficiency (big I(Z;Y)).
But as pointed out in the literature several times, the fact that neural networks implement a deterministic map makes these information theoretic quantities degenerate:
There are attempts at solving these problems in the literature, but the solutions so far are unsatisfying: they're either very adhoc, rely on questionable assumptions, lack clear operational interpretation, introduce new problems, or seem theoretically intractable.
Treat the weight as stochastic:
This paper (also relevant) defines several notions of information measure relative to an arbitrary choice of p(w) and q(w|D) (not a Bayesian posterior):
I like their idea of using shannon information measures to try to capture a notion of “robustly” shared information. but the attempts above so far seem pretty ad hoc and reliant on shaky assumptions. i suspect SLT would be helpful here (just read the paper and see things like casually inverting the fisher information matrix).
Use something other than shannon information measures:
There’s V-information which is a natural extension of shannon information measures when you restrict the function class to consider (due to e.g., computational constraints). But now the difficult question is the choice of natural function class. Maybe linear probes are a natural choice, but this still feels ad hoc.
There’s K-complexity, but there's the usual uncomputability and the vibes of intractability in mixing algorithmic information theory notions with neural networks when the latter has more of a statistical vibe than algorithmic. idk, this is just really vibes, but I am wary of jumping to the conclusion of thinking AIT is necessary in information theoretically analyzing neural networks based on the "there's determinism and AIT is the natural playing field for deterministic information processing systems"-type argument.
Ideally, I could keep using the vanilla shannon information measures somehow because they’re nice and simple and computable and seems potentially tractable both empirically and theoretically.
And so far, I haven't been able to find a satisfying answer to the problem. I am curious if anyone has takes on this issue.