I've noticed that when trying to understand a math paper, there are a few different ways my skill level can be the blocker. Some of these ways line up with some typical levels of organization in math papers:
- Definitions: a formalization of the kind of objects we're even talking about.
- Theorems: propositions on what properties are true of these objects.
- Proofs: demonstrations that the theorems are true of the objects, using known and accepted previous theorems and methods of inference.
Understanding a piece of math will require understanding each of these things in order. It can be very useful to identify which of type of thing I'm stuck on, because the different types can require totally different strategies.
Beyond reading papers, I'm also trying to produce new and useful mathematics. Each of these three levels has another associated skill of generating them. But it seems to me that the generating skills go in the opposite order.
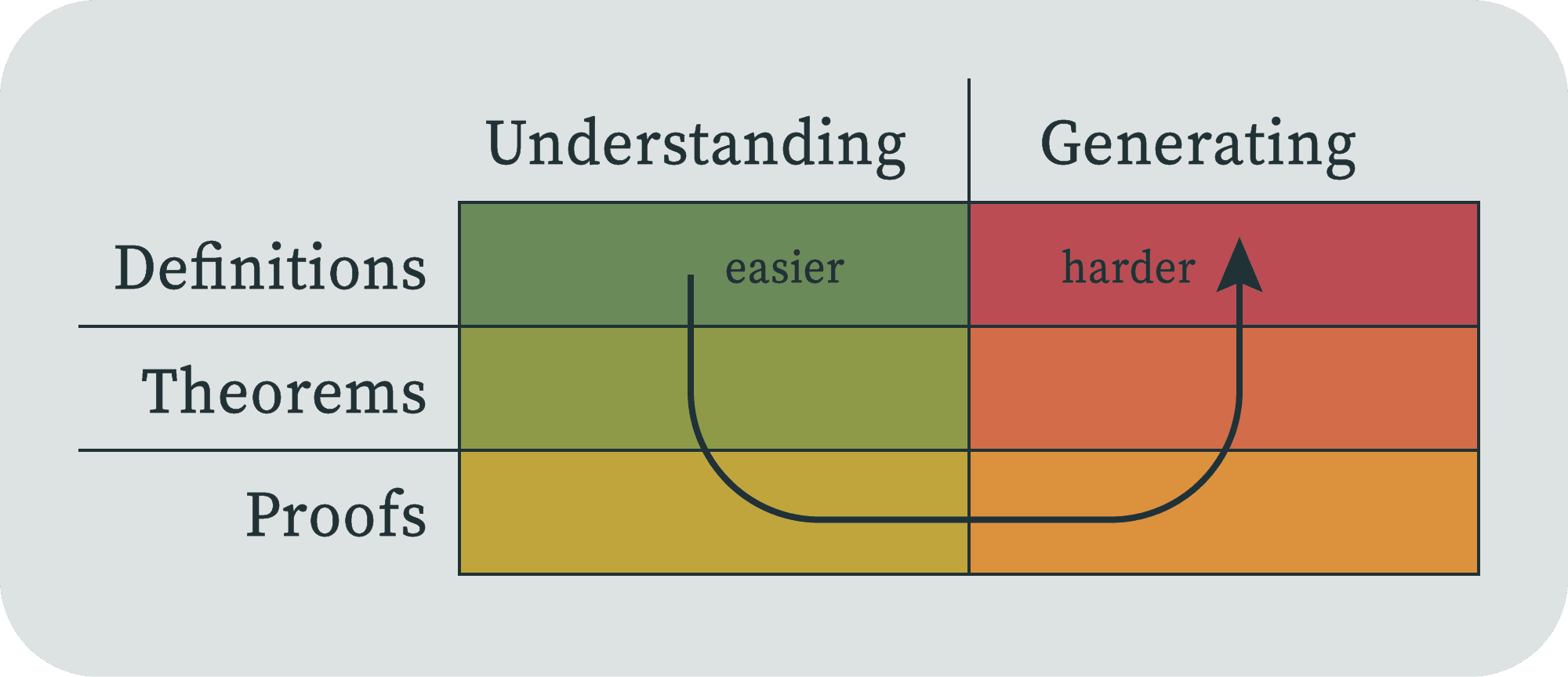
This feels like an elegant mnemonic to me, although of course it's a very simplified model. Treat every statement below as a description of the model, and not a claim about the totality of doing mathematics.
Understanding
Understanding these more or less has to go in the above order, because proofs are of theorems, and theorems are about defined objects. Let's look at each level.
Definitions
You might think that definitions are relatively easy to understand. That's usually true in natural languages; you often already have the concept, and you just don't happen to know that there's already a word for that.
Math definitions are sometimes immediately understandable. Everyone knows what a natural number is, and even the concept of a prime number isn't very hard to understand. I get the impression that in number theory, the proofs are often the hard part, where you have to come up with some very clever techniques to prove theorems that high schoolers can understand (Fermat's last theorem, the Collatz conjecture, the twin primes conjecture).
In contrast, in category theory, the definitions are often hard to understand. (Not because they're complicated per se, but because they're abstract.) Once you understand the definitions, then understanding proofs and theorems can be relatively immediate in category theory.
Sometimes the definitions have an immediate intuitive understanding, and the hard part is understanding exactly how the formal definition is a formalization of your intuition. In a calculus class, you'll spend quite a long time understanding the derivative and integral, even though they're just the slope of the tangent and the area under the curve, respectively.
You also might think that definitions were mostly in textbooks, laid down by Euclid or Euler or something. At least in the fields that I'm reading papers from, it seems like most papers have definitions (usually multiple). This is probably especially true for papers that are trying to help form a paradigm. In those cases, the essential purpose of the paper is to propose the definitions as the new paradigm, and the theorems are set forth as arguments that those definitions are useful.
Theorems
Theorems are in some sense the meat of mathematics. They tell you what you can do with the objects you've formalized. If you can't do anything meaty with an object, then you're probably holding the wrong object.
Once you understand the objects of discussion, you have to understand what the theorem statement is even saying. I think this tends to be more immediate, especially because often, all the content has been pushed into the definitions, and the theorem will be a simpler linking statement, like "all As are Bs" or "All As can be decomposed into a B and a C".
For example, the fundamental theorem of calculus tells you that the derivative and the integral are opposites, which is a simple to understand statement if you already know what those two things are. Rice's theorem tells us that all non-trivial semantic properties of programs are undecidable, which is simple to understand if you already know what "non-trivial", "semantic property", "program" and "undecidable" mean.
When reading a paper I often get to the theorem statement and only then realize that I actually poorly understood the previously defined terms. Perhaps that's because the theorem seems obviously false to me. More often, I'll read the theorem statement, and it will just be a bunch of symbols. If I'm only very tenuously holding the definitions in my head, then I can't simultaneously think about them all and manipulate them in the ways that would be necessary to understand the theorem statement.
Proofs
People often think of understanding proofs as the hard part of learning math.
In some sense, the point of proving theorems is so that others don't have to understand the proof to make use of the result. Theorem statements are like interfaces that abstract away from the details of the proof. You can go away remembering the compressed theorem, and, since it's definitely true, you don't have to worry about why.[1] But if your goal is to be able to make substantive progress in mathematics, then you really do need to understand why the theorem is true.
This is essentially why engineers learn theorems, and mathematicians learn proofs.
I think of there as being three ways to understand a theorem. The first is to be able to verify that each step of the proof is a valid manipulation of the symbols. I find that this way often happens first (especially if I'm still hazy on the definitions). The great thing about math is that's technically all you need.
The second way is to "see" why it's true with your intuition. If you can see how derivatives are slopes from a position graph, and integrals as areas under speed graphs, then it may feel very obvious that the area under the speed graph is the difference between the start and end point of the position graph. This is a key skill to being a mathematician, but it's very different from being able to apply the epsilon-delta definitions to rigorously prove the fundamental theorem of calculus.
The third way to understand a theorem is to understand why the first way is the same thing as the second way. That is, you should be able to understand why the symbolic manipulation is a formalization of the intuition.[2] I think it is very common not to achieve this level of understanding for a particular proof. I would guess that most math students go through most math classes without understanding things at this level. And to some degree, this is a demonstration of why mathematics is such an effective tool for society; you don't have to deeply understand the results to productively build with them.
Very often, I find that understanding the proof dramatically improves my understanding of the definitions (noticing a theme here?). It makes it much clearer to see why they were crafted how they were, or under which types of cases the theorem doesn't hold. But especially, understanding proofs means you're gaining skill in understanding how proofs work, how they actually bring about the conclusion. Proofs are made of techniques, which are modular mechanisms that can be brought to bear on other problems. And that's what will get you the next level of skill.
Generating
After you've attained a skill level that lets you fully understand a proof, the next level of skill is where you could have generated the proofs yourself, given the theorem statement. After that it goes backward; given the definitions, can you generate the theorem? And given only a pre-formal understanding of the domain, can you generate the definitions?
Proofs
Being able to prove theorems is a huge part of what you are aiming for when training to become a mathematician. And I think it's also often a sufficient level of skill. There are many domains where there are conjectures left and right, and the shortage is in proving them.
You may be thinking about some famous conjectures whose proofs would be the ultimate high-status accomplishment, such as the Riemann hypothesis or P = NP. But I think these are so famous exactly because they are exceptional; once someone has located a very very convincing conjecture, it's usually relatively easy to prove it. Usually the reasons we believe them are the essence of why they're true, and thus we can locate a proof by translating our reasons into the formal math. So when the proof resists being found, it becomes even more conspicuous and interesting. Proving theorems is also a challenge that is well-suited to prizes, because solutions are objectively validatable. It would be significantly harder to judge a prize for someone to come up with great conjecture (let alone great definitions).
Theorems
Generating interesting theorems in a domain requires quite a lot of insight and creativity. Many simple theorems will follow naturally from definitions; these are often considered "basic properties" or "lemmas". An example would be the linearity of the derivative, or the chain rule, or the infinitude of primes. Checking examples is also a form of theorem; for example, you could check whether a property holds for the empty set, or the identity function. These kind of checks can usually be done as part of understanding definitions (and will be a basic skill for working mathematicians).
But interesting theorems will be ones with more semantic content behind them. They will make use of every part of the definition of the objects. They will feel powerful, in the sense that they let you get results elsewhere that you couldn't before.
Towards the more interesting end of this spectrum are the theorems that get named after people, or are perhaps even called the "fundamental theorem" of the domain. Most mathematicians will not be trying to achieve something quite this big (depending on how specialized their domain is).
Definitions
Finally, we come to the skill that this model places at the highest level: generating definitions.
What makes definitions hard is that you have to generate them given nothing. You're not given literally nothing; you're just given nothing formal. You generate definitions by thinking about whatever real-world domain you choose, and attempting to usefully formalize something about it. The search space is about as big as it could be.
Often, the purpose of definitions is that you've noticed some interesting phenomenon in your domain, and you're pretty sure that you could make it a theorem out of it, if only you could pinpoint the right objects. Sometimes you even get the definitions by trying to prove your idea about a rough guess at the type of object, and then finding the ways that doesn't work, and then excluding those ways by adding these as constraints in the definitions (for example, that something will hold "almost surely", or "up to isomorphism" or "for all primes greater than 2").
Sometimes, humanity figured out the right theorems without quite nailing the definitions. The main theorems of calculus emerged in the late 1600s (with significant conceptual precursor work for two thousand years) but the modern epsilon-delta definition of limits wasn't fully formed until the 1800s. Probability theory had intuitive results for a few hundred years before Kolmogorov found an axiomatization (1933) that gained consensus. This was long after other quite advanced results like the law of large numbers (1713) and the central limit theorem (1811).
Or sometimes there are multiple reasonable definitions. A standard topological space is defined as a set of open sets of "points" with various properties, but you can also get most of the results from a pointless version of topology that instead uses a lattice to represent the relationship between the open sets. Computability theory was famously founded in part by showing that several formal models of computation were equivalent.
As I mentioned in the beginning, many if not most of the papers I read contain multiple novel definitions. Are these authors executing the highest level of mathematical skill? Not really; as implied above, the main success criterion is not simply that you found some definition for which you could state and prove some theorem. The main criterion, at least in the context of science as a societal project, is broad acceptance of your definitions as useful, whereafter other researchers begin to add to the theory that your definitions delineate. Some relatively modern examples where this happened include PAC learning, various degrees of algorithmic randomness, and the definition of a chaotic system.
Skill improvement
If I'm stuck on understanding a definition, then I often try to draw out a canonical-feeling picture, or a few different pictures of different examples. I aim to develop what K. Anders Ericsson calls mental representations: cognitive "chunks" that efficiently represent the relevant concept, which allow fluent manipulation.
If I'm stuck at understanding a theorem statement, then perhaps I can rearrange the picture to capture the theorem naturally. Or perhaps I need to grok some earlier, simpler theorems about the objects. Or perhaps I need to read through a counter-example.
If I'm stuck understanding a proof, then maybe it's because I don't understand a particular proof method. Maybe I need to go find some easier proofs in the domain. Maybe I should check my intuition for whether the theorems "should" be true or false, and try to generate my own proof based on that. Then I can check whether the presented proof captures any of that structure. Another great way to understand a proof is to try to prove the theorem yourself before even looking at the proof. If you fail, the proof can help you learn how you could have been thinking about the problem instead. If you succeed, then the differences between your proof and the original could be very informative!
If I'm stuck at a generating stage, that's because the generating stage is what it means to be doing original research, which is just a continual journey of progress through perpetual stuckness. I could perhaps better give better advice on this once I consider myself to have any results.
Paradigm formation starts at the end
I recurringly check in with myself about whether I think my current skill level and output is appropriate for what I'm trying to do. Mostly, I do this for the "understanding" stages. If I were working in a field with a more established paradigm, like Lie group theory or algorithmic randomness, then I would expect myself to be doing some things earlier in the "generating" stack, like generating proofs of open problems. But as it is, I'm working in a field with no paradigm.
Part of what makes something a new paradigm in math is that the old definitions are no longer the useful ones for continued progress. The open problems are generating the definitions: generating the definitions that lead to proofs of theorems that usefully capture truths about the domain.
Since (in this model) generating definitions is the highest level of skill, I certainly cannot reliably do it yet.
- ^
Of course, this only works if you can successfully remember all the technical assumptions enough to be sure that it applies to your application. For example, you should remember to check whether your function is integrable, or that your outcome isn't in the measure-zero set.
- ^
I'll caveat this by saying that I think there is a type of mathematician—one that can be equally powerful—that operates fully at the level of symbolic manipulation. Presumably they do this by building up lots of skills, heuristics, and ultimately "intuitions" of the symbolic flavor. This feels magical to me, but is also a power that I would like to attain.
I think the problem to grapple with is that I can cover the rationals in [0,1] with countably many intervals of total length only 1/2 (eg enumerate rationals in [0,1], and place interval of length 1/4 around first rational, interval of length 1/8 around the second, etc). This is not possible with reals -- that's the insight that makes measure theory work!
The covering means that the rationals in an interval cannot have a well defined length or measure which behaves reasonably under countable unions. This is a big barrier to doing probability theory. The same problem happens with ANY countable set -- the reals only avoid it by being uncountable.