Mathematician, alignment researcher, doctor. Reach out to me on Discord and tell me you found my profile on LW if you've got something interesting to say; you have my explicit permission to try to guess my Discord handle if so. You can't find my old abandoned-for-being-mildly-infohazardously-named LW account but it's from 2011 and has 280 karma.
A Lorxus Favor is worth (approximately) one labor-day's worth of above-replacement-value specialty labor, given and received in good faith, and used for a goal approximately orthogonal to one's desires, and I like LessWrong because people here will understand me if I say as much.
Apart from that, and the fact that I am under no NDAs, including NDAs whose existence I would have to keep secret or lie about, you'll have to find the rest out yourself.
Posts
Wikitag Contributions
What are "latential" string diagrams?
Just the word I use to describe "thing that has something to do with (natural) latents". More specifically for this case: a string diagram over a Markov category equipped with the extra stuff, structure, and properties that a Markov category needs to have in order to faithfully depict everything we care about when we want to write down statements or proofs about Bayes nets which might transform in some known restricted ways.
What does it it mean that you can't derive them all from a "fixed" set? Do you imagine some strong claim e.g. that the set of rewriting rules being undecidable, or something else?
Something else. I'm saying that:
- You would need to pick your set of identities once and for all at the start, as part of specifying what extra properties the category has; you could totally use those as (or to derive) some of the rules (and indeed I show how you can do just that for Breakout Joint Independence)
- Binary operations like Frankenstein or Stitching probably don't fall out of an approach like that (they look a lot more like colimits
- Rules which a categorical approach trivializes like Factorization Transfer don't particularly fall out of an approach like that
- You could probably get some kind of "ruleset completeness" result if you had a strong sense of what would constitute a complete ruleset - the paper I linked above looks to be trying to do this
...so maybe some approach where you start by listing off all the identities you want to have hold and then derive the full ruleset from those would work at least partially? I guess I'm not totally clear what you mean by "categorical axioms" here - there's a fair amount that goes into a category; you're setting down all the rules for a tiny toy mathematical universe and are relatively unconstrained in how you do so, apart from your desired semantics. I'm also not totally confident that I've answered your question.
Okay, so this is not what you care about? Maybe you are saying the following: Given two diagrams X,Y, we want to ask whether any distribution compatible with X is compatible with Y. We don't ask whether the converse also holds. This is a certain asymmetric relation, rather than an equivalence.
Yes. Well... almost. Classically you'd care a lot more about the MEC, but I've gathered that that's not actually true for latential Bayes nets. For those, we have some starting joint distribution J, which we care about a lot, and some diagram D_J which it factors over; alternatively, we have some starting set of conditionality requirements J, and some diagram D_J from among those that realize J. (The two cases are the same apart from the map that gives you actual numerical valuations for the states and transitions.)
We do indeed care about the asymmetric relation of "is every distribution compatible with X also compatible with Y", but we care about it because we started with some X_J and transformed it such that at every stage, the resulting diagram was still compatible with J.
that's not a thing that really happens?
What is the thing that doesn't happen? Reading the rest of the paragraph only left me more confused.
Somehow being able to derive all relevant string diagram rewriting rules for latential string diagrams, starting with some fixed set of equivalences? Maybe this is just a framing thing, or not answering your question, but I would expect to need to explicitly assume/include things like the Frankenstein rule - more generally, picking which additional rewriting rules you want to use/include/allow is something you do in order to get equivalence/reachability in the category to line up correctly with what you want that equvialence to mean - you could just as soon make those choices poorly and (e.g.) allow arbitrary deletions of states, or addition of sampling flow that can't possibly respect causality; we don't do that here because it wouldn't result in string diagram behavior that matches what we want it to match.
I think I may have misunderstood, though, because that does sounds almost exactly like what I found to happen for the Joint Independence rule - you have some stated equivalence, and then you use string diagram rewriting rules common to all Markov category string diagrams in order to write the full form of the rule.
Simple form of the JI Rule - note the equivalences in the antecedent, which we can use to prove the consequent, not just enforce the equivalence!
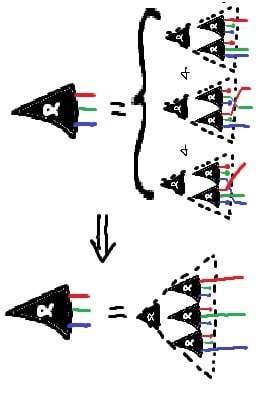
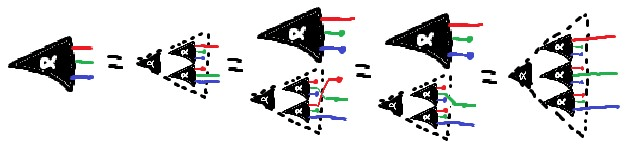
we don't quite care about Markov equivalence class
What do you mean by "Markov equivalence class"?
Two Bayes nets are of the same Markov equivalence class when they have precisely the same set of conditionality relations holding on them (and by extension, precisely the same undirected skeleton). You may recognize this as something that holds true when applicable for most of these rules, notably (sometimes) including the binary operations and notably excluding direct arrow-addition; additionally, this is something that applies for abstract Bayes nets just as well as concrete ones.
Hi! I spent some time working on exactly this approach last summer at MATS, and since then have kept trying to work out the details. It's been going slowly but parts of it have been going at all.
My take regarding your and @Alexander Gietelink Oldenziel's comments below is - that's not a thing that really happens? You pick the rules and your desired semantics first, and then you write down your manipulation rules to reflect those. Maybe it turns out that you got it wrong and there's more (or fewer!) rules of derivation to write down, but as long as the rules you wrote down follow some very easy constraints, you can just... write down anything. Or decline to. (Also, from a quick read I'm fairly sure you need a little bit more than just "free cartesian category" to hold of your domain category if you want nice structures to hang state/kernel-labels on. You want to be able to distinguish a concrete Bayes net (like, with numbers and everything) from an abstract "Bayes net", which is just a directed acyclic graph representing local conditionality structures - though we should note that usually people working with Bayes nets assume that we actually have trees, and not just DAGs!)
Maybe there's arguments from things like mathematical elegance or desired semantics or problematizing cases to choose to include or exclude some rule, or formulate a rule in one or another way, but ultimately you get to add structure to a category as suits you.
- Can we derive a full classification of such rules?
Probably there's no full classification, but I think that a major important point (which I should have just written up quickly way way long ago) is that we don't quite care about Markov equivalence class - only about whether any given move takes us to a diagram still compatible with the joint distribution/factorization that we started with.
- Is there a category-theoretic story behind the rules? Meaning, is there a type of category for which Bayes nets are something akin to string diagrams and the rules follow from the categorical axioms?
In my understanding there's a pretty clear categorical story - some of which are even just straight trivial! - to most of the rules. They make good sense in the categorical frame; some of them make so much sense that they're the kind of thing string diagrams don't even bother to track. I'm thinking of Factorization Transfer here, though the one major thing I've managed to get done is that the Joint Independence rule actually follows as a quick technical lemma from its assumptions/setup, rather than having to be assumed.
There's noncanonical choices getting made in the two "binary operation" rules, but even then it seems to me like the fact that we only ever apply that operation to two diagrams of the same "flavor" means we should likely only ever get back another diagram of the same "flavor"; apart from that, there's a strong smell of colimitness to both of those rules, which has kept me mulling over whether there's a useful "limitish" sort of rule that John and David both missed. Underlying this is my suspicion that we might get a natural preorder structure on latent Bayes nets/string diagrams as the pullback of the natural lattice on Markov equivalence classes, where one MEC is above another if it has strictly more conditionality relationships in it - i.e. the unique minimal element of the lattice is "everything is independent", and there's lots of maximal elements, and all our rules need to keep us inside the preimage of the upset of our starting MEC.
Which is to say: yes, yes there totally is such a type of category, but existing work mostly stopped at "Bayes nets akin to string diagrams", although I've seen some non-me work lately that looks to be attacking similar problems.
I think you maybe miss an entire branch of the tech-tree here I consider important - the bit about the Lindy case of divination with a coin-flip and checking your gut. It doesn't stop at a single bit in my experience; it's something you can use more generally to get your own read on some situation much less filtered by masking-type self-delusion. At the absolute least, you can get a "yes/no/it's complicated" out of it pretty easily with a bit more focusing!
I claim that divination[1] is specifically a good way for routing around the worried self-deception and yeah-sure-whatever daily frames and getting at how you really feel about something you're clearly uncertain-and-high-arousal enough about to Do A Divination about.
As a maybe-tangent, a friend of mine has a self-designed divination method I like a lot but haven't managed to fully learn how to do; what I like about it is its compositionality/modularity, where you pull a handful (3-5 IIRC) of symbolic rune-type things from a bag and toss them onto a surface, such that both the divination-tiles you pulled out and their relative-location/absolute-location/orientation/pointing-with-respect-to-each-other all matter. I don't think I have a maximally good sense of why I like it so much past the obvious factors of "fun system/novelty/a friend made this" and "fine-grained expressive power" and "combinatorial explosion power", though.
For my own part I like to use coins that I've made for other reasons for this purpose. They're not fair coins; that's the fun part.
- ^
In the explicit epistemic frame of "we are getting the bits of interest from some internal mental process to use for planning/self-check purposes", mind you!
Maybe this is the right place to ask/discuss this, and maybe not - if it's not; say so and I'll stop.
IIRC you (or maybe someone once mentioned hearing about people who try to [experience the first jhana][1] and then feeling pain as a result, and that you didn't really understand why that happened. There was maybe also a comment about "don't do that, that sounds like you were doing it wrong".
After some time spent prodding at myself and pulling threads and seeing where they lead... I am not convinced that they were doing it wrong at all. There's a kind of way you can end up where the application of that kind of comfort/pleasure/positive-valence is, of itself, painful/aversive/immiserating, if not necessarily enduringly so. Reframing it
I don't have a full explicit model for it, so here's some metaphors that hopefully collectively shed light:
- Hunger beyond reason, hunger for weeks, hunger to the point of starvation. A rich and lavish meal set before you, of all your favorite foods and drinks, prepared expertly. A first bite - overwhelming; so perfect and so intense. You toy with the idea of eating nothing more and find you can neither eat nor decline - at least not comfortably. You gorge yourself and die of refeeding syndrome.
- Dreams of your childhood home, of the forests around it, of the sparkling beauty of the night sky. The building was knocked down years ago, the forest cut, the sky bleached with light pollution, all long after you moved away anyway.
- Like the itch/pain of a healing wound, or of a limb fallen asleep, or an amputated limb. Like internal screaming or weeping, suddenly given voice.
- Like staring at something dazzlingly bright and incomparably precious, even coveted; especially one that you can't touch or even reach - a sapphire the size of your fist, say, or the sun. What would you even do with those, really, if you could grab them?
- ^
Not sure if my terminology is correct here - I'm talking about doing the meditation/mental-action process itself. You know, the one which causes you tons of positive valence in a way you like but don't want.
Here's a game-theory game I don't think I've ever seen explicitly described before: Vicious Stag Hunt, a two-player non-zero-sum game elaborating on both Stag Hunt and Prisoner's Dilemma. (Or maybe Chicken? It depends on the obvious dials to turn. This is frankly probably a whole family of possible games.)
The two players can pick from among 3 moves: Stag, Hare, and Attack.
Hunting stag is great, if you can coordinate on it. Playing Stag costs you 5 coins, but if the other player also played Stag, you make your 5 coins back plus another 10.
Hunting hare is fine, as a fallback. Playing Hare costs you 1 coin, and assuming no interference, makes you that 1 coin back plus another 1.
But to a certain point of view, the richest targets are your fellow hunters. Preparing to Attack costs you 2 coins. If the other player played Hare, they escape you, barely recouping their investment (0 payoff), and you get nothing for your boldness. If they played Stag, though, you can backstab them right after securing their aid, taking their 10 coins of surplus destructively, costing them 10 coins on net. Finally, if you both played Attack, you both starve for a while waiting for the attack, you heartless fools. Your payoffs are symmetric, though this is one of the most important dials to turn: if you stand to lose less in such a standoff than you would by getting suckered, then Attack dominates Stag. My scratchpad notes have payoffs at (-5, -5), for instance.
To resummarize the payoffs:
- (H, H) = (1, 1)
- (H, S) = (1, -5)
- (S, S) = (10, 10)
- (H, A) = (0, -2)
- (S, A) = (-10(*), 20)
- (A, A) = (-n, -n); n <(=) 10(*) -> A >(=) S
So what happens? Disaster! Stag is dominated, so no one plays it, and everyone converges to Hare forever.
And what of the case where n > 10? While initially I'd expected a mixed equilibrium, I should have expected the actual outcome: the sole Nash equilibrium is still the pure all-Hare strategy - after all, we've made Attacking strictly worse than in the previous case! (As given by https://cgi.csc.liv.ac.uk/~rahul/bimatrix_solver/ ; I tested n = 12.)
A snowclone summarizing a handful of baseline important questions-to-self: "What is the state of your X, and why is that what your X's state is?" Obviously also versions that are less generally and more naturally phrased, that's just the most obviously parametrized form of the snowclone.
Classic(?) examples:
"What do you (think you) know, and why do you (think you) know it?" (X = knowledge/belief)
"What are you doing, and why are you doing it?" (X = action(-direction?)/motivation?)
Less classic examples that I recognized or just made up:
"How do you feel, and why do you feel that way?" (X = feelings/emotions)
"What do you want, and why do you want it?" (X = goal/desire)
"Who do you know here, and how do you know them?" (X = social graph?)
"What's the plan here, and what are you hoping to achieve by that plan?" (X = plan)
Say more about "ray-tracing"? What does that look like? And do you have a bullshit-but-useful PCA-flavored breakdown of those few dimensions of variation?