This is a linkpost for Apollo Research's new interpretability paper:
We introduce a new method for directly decomposing neural network parameters into mechanistic components.
Motivation
At Apollo, we've spent a lot of time thinking about how the computations of neural networks might be structured, and how those computations might be embedded in networks' parameters. Our goal is to come up with an effective, general method to decompose the algorithms learned by neural networks into parts that we can analyse and understand individually.
For various reasons, we've come to think that decomposing network activations layer by layer into features and connecting those features up into circuits (which we have started calling 'mechanisms'[1]) may not be the way to go. Instead, we think it might be better to directly decompose a network's parameters into components by parametrising each mechanism individually. This way, we can directly optimise for simple mechanisms that collectively explain the network's behaviour over the training data in a compressed manner. We can also potentially deal with a lot of the issues that current decomposition methods struggle to deal with, such as feature splitting, multi-dimensional features, and cross-layer representations.
This work is our first attempt at creating a decomposition method that operates in parameter space. We tried out the method on some toy models that tested its ability to handle superposition and cross-layer representations. It mostly worked the way we hoped it would, though it's currently quite sensitive to hyperparameters and the results have some imperfections. But we have ideas for fixing these issues, which we're excited to try.
What we do
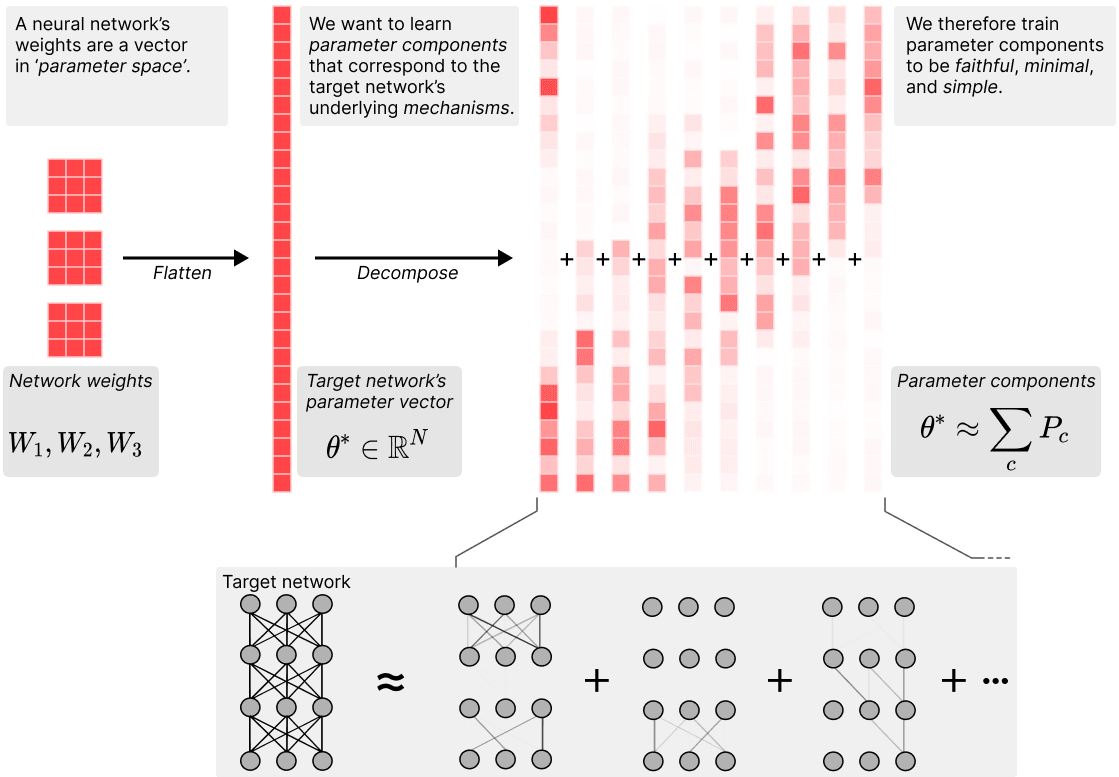
Our method decomposes the network parameter vector into a sum of parameter component vectors, such that the average description length of the mechanisms used on any one data point across the training dataset is minimised. A 'parameter component' here is a vector in parameter space that is supposed to correspond to a specific mechanism of the network. For example, if the network has stored the fact that `The sky is blue' in its parameters, the weights that make up the query-key lookup for this fact could be one such component. These components of the learned network algorithm do not need to correspond to components of the network architecture, such as individual neurons, layers, or attention heads. For example, the mechanism for `The sky is blue' could be spread across many neurons in multiple layers of the network through cross-layer superposition. Components can also act on multi-dimensional features. On any given data point, only a small subset of the components in the network might be used to compute the network output.
We find the parameter components by optimising a set of losses that make the components:
Faithful: The component vectors () must sum to the parameter vector of the original network (). We train for this with an MSE loss .
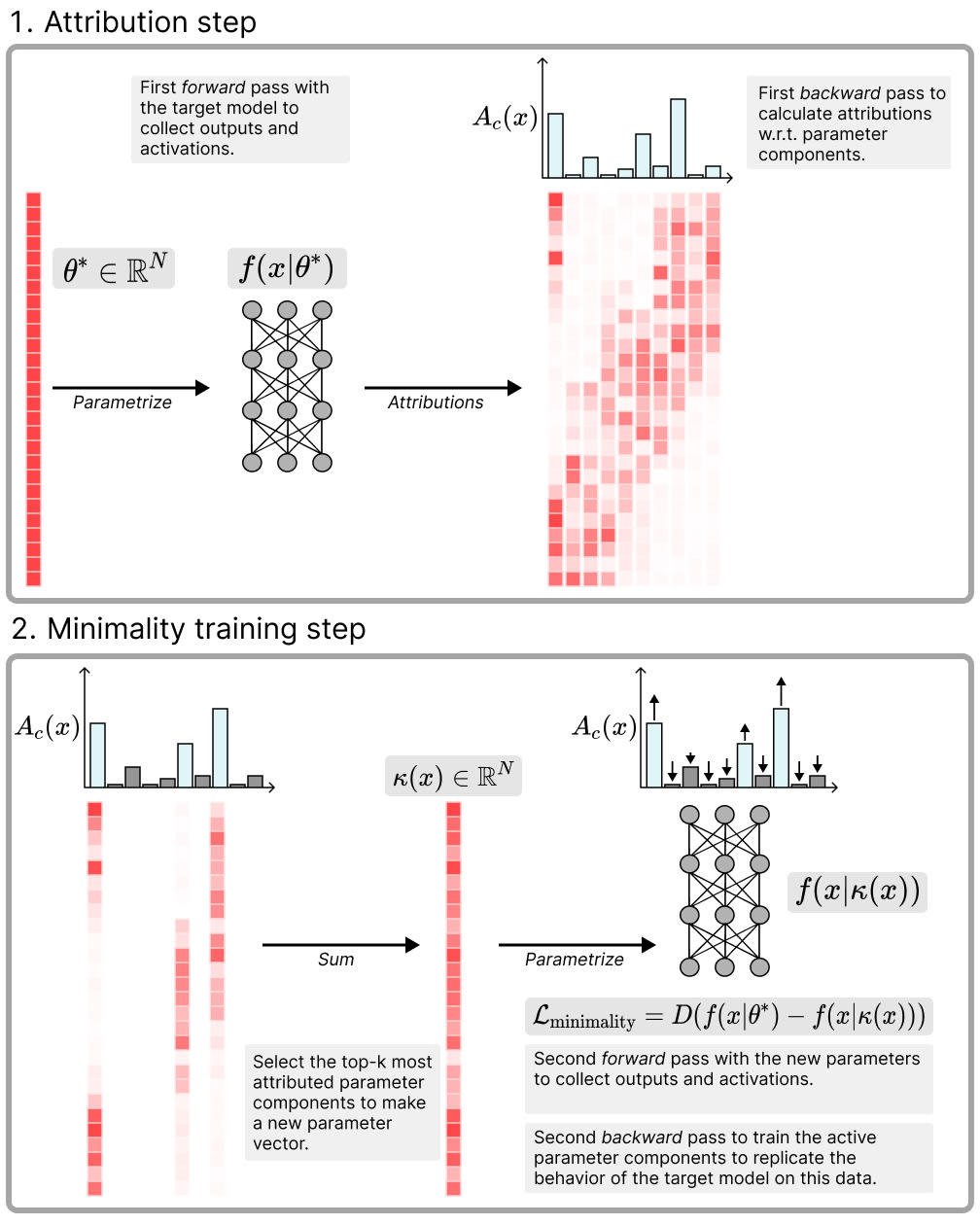
Minimal: As few components as possible should be used to replicate the network's behavior on any given data point in the training data set. We operationalise this with a top- test based on attributions: First we run the original model and use gradient attributions to estimate the attribution of each parameter component to the final network output. Then, we use batch top- (as in BatchTopK SAEs) to select the parameter components with the highest attributions across a batch. We sum these top- components to obtain a new parameter vector , and use it to perform a second forward pass with these new parameters. Then we train to match the original model's output by minimising an MSE loss between the network outputs on the two forward passes, thereby increasing the attributions of the active components on that data.[2]
Simple: Individual parameter components should be simpler than the whole weight vector, in the sense of having a shorter description length. We aim to minimise the sum of the ranks of all the matrices in active components as a proxy of description length. In practice we use the 'Schatten quasi-norm' (which is just the norm of a matrices' singular values) to optimize that objective.[3]
These losses can be understood as trying to minimise a proxy for the total description length per data point of the components that have a causal influence on the network's output, across the training data set.
We test our method on a set of three toy models where the ground truth decomposition of the network algorithm is known: (1) A toy model of features in superposition (TMS), (2) A toy model that implements more computations than it has neurons, and (3) A model that implements more computations than it has neurons distributed across two layers.
We find that APD is largely able to decompose these toy networks into components corresponding to individual mechanisms: (1) The weights for individual features in superposition in the TMS model; and (2) & (3) The weights implementing individual computations across different neurons in the compressed computation models. However, the results required a lot of hyperparameter tuning and still exhibit some amount of mechanism mixing, which we suspect is due to our using top-k.
While we think this first prototype implementation is too sensitive to hyperparameters to be usefully applied to larger models such as LLMs, we think there are ways to overcome these issues. Overall, we think the general approach of directly decomposing networks into components directly in parameter space is promising.
Future work
We have some pretty clear ideas on where we want to take the method next and would be excited to hear from others who are interested in using or improving the method. We think some reasonable next steps are:
- Make the method more stable: Currently, the optimisation process in APD can be painfully brittle. Lots of hyperparameter tuning can be required to get good results. We have some ideas for fixing this that we're excited about. First and foremost, we want to switch out the attributions for trained masks that are optimised along with the components. This involves some changes to our loss function to ensure the resulting masks still represent valid component activations in the sense we discuss in Appendix A.
- Make the method more efficient: We have some ideas for making APD more computationally efficient at scale. For example, we think it should be possible to save on a lot of compute by running the optimisation in two stages: First we decompose the network into rank-1 components, then we group those rank-1 pieces together into higher rank components in the configuration that minimises overall description length per data point.[4][5]
- Implementation for transformers and CNNs: Since APD operates on network parameters, it seems mostly straightforward to adapt to any neural network architecture based on matrix multiplications. The only change seems to be that we might want to have different parameter components active at different token positions or coordinates in a CNN input tensor. Nevertheless, we need to actually create an implementation and test it on toy models where we have ground truth understanding of the mechanisms in the network.
- Scaling to LLMs: We will want to apply the method to LLMs. Probably starting with a decomposition at a single layer rather than the entire networks. The results could then be compared and contrasted with the features SAEs find in those networks.
- ^
- ^
KL-divergence could be used here as well, depending on the target model.
- ^
This is a standard trick in low-rank optimisation. It's somewhat analogous to how penalising the pseudonorm with of activations in an SAE can do an alright job at optimising for low .
- ^
- ^
We also noticed that restricting component rank tends to make the method more stable, so we think this change will help with the previous point as well.
Really cool work!
Would it be accurate to say that MoE models are an extremely coarse form of parameter decomposition? They check the box for faithfulness, and they're an extreme example of optimizing minimality (each input x only uses one component of the model if you define each expert as a component) while completely disregarding simplicity.
Kind of? I'd say the big difference are
MOE experts don't completely ignore 'simplicity' as we define it in the paper though. A single expert is simpler than the whole MOE network in that it has lower rank/ fewer numbers are required to describe its state on any given forward pass.