Produced As Part Of The OxAI Safety Labs program, mentored by Joar Skalse.
TL;DR
This is a blog post introducing our new paper, "Goodhart's Law in Reinforcement Learning" (to appear at ICLR 2024). We study Goodhart's law in RL empirically, provide a geometric explanation for why it occurs, and use these insights to derive two methods for provably avoiding Goodharting.
Here, we only include the geometric explanation (which can also be found in the Appendix A) and an intuitive description of the early-stopping algorithm. For the rest, see the linked paper.
Introduction
Suppose we want to optimise for some outcome, but we can only measure an imperfect proxy that is correlated, to a greater or lesser extent, with that outcome. A prototypical example is that of school: we would like children to learn the material, but the school can only observe the imperfect proxy consisting of their grades. When there is no pressure exerted on students to do well on tests, the results will probably reflect their true level of understanding quite well. But this changes once we start putting pressure on students to do get good grades. Then, the correlation usually breaks: students learn "for the test", cheat, or use other strategies which make them get better marks without necessarily increasing their true understanding.
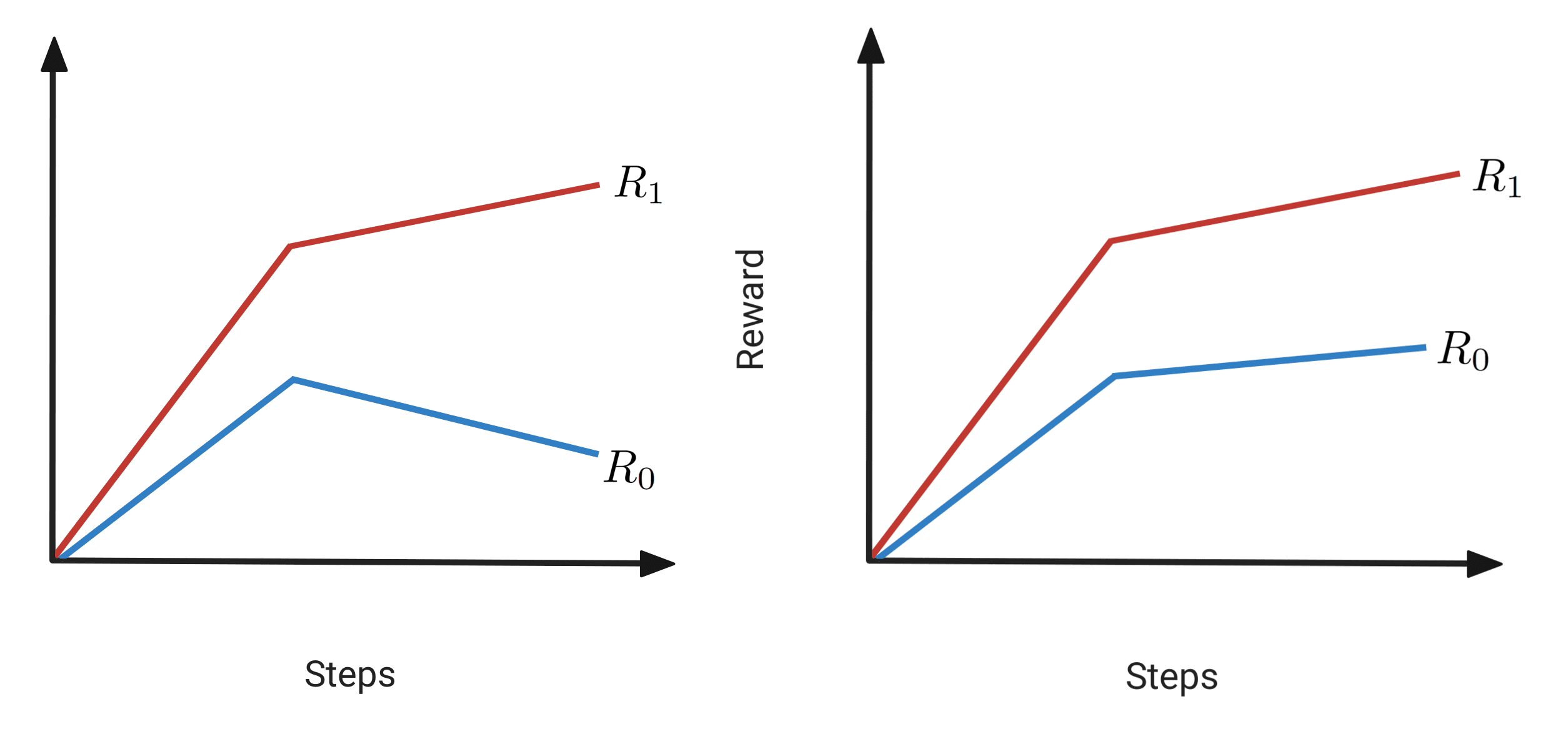
That "any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes" (or "when a measure becomes a target, it ceases to be a good measure") is called the Goodhart's law. Graphically, plotting the true reward and the proxy reward obtained along increasing optimisation pressure, we might therefore expect to see something like the following graph:
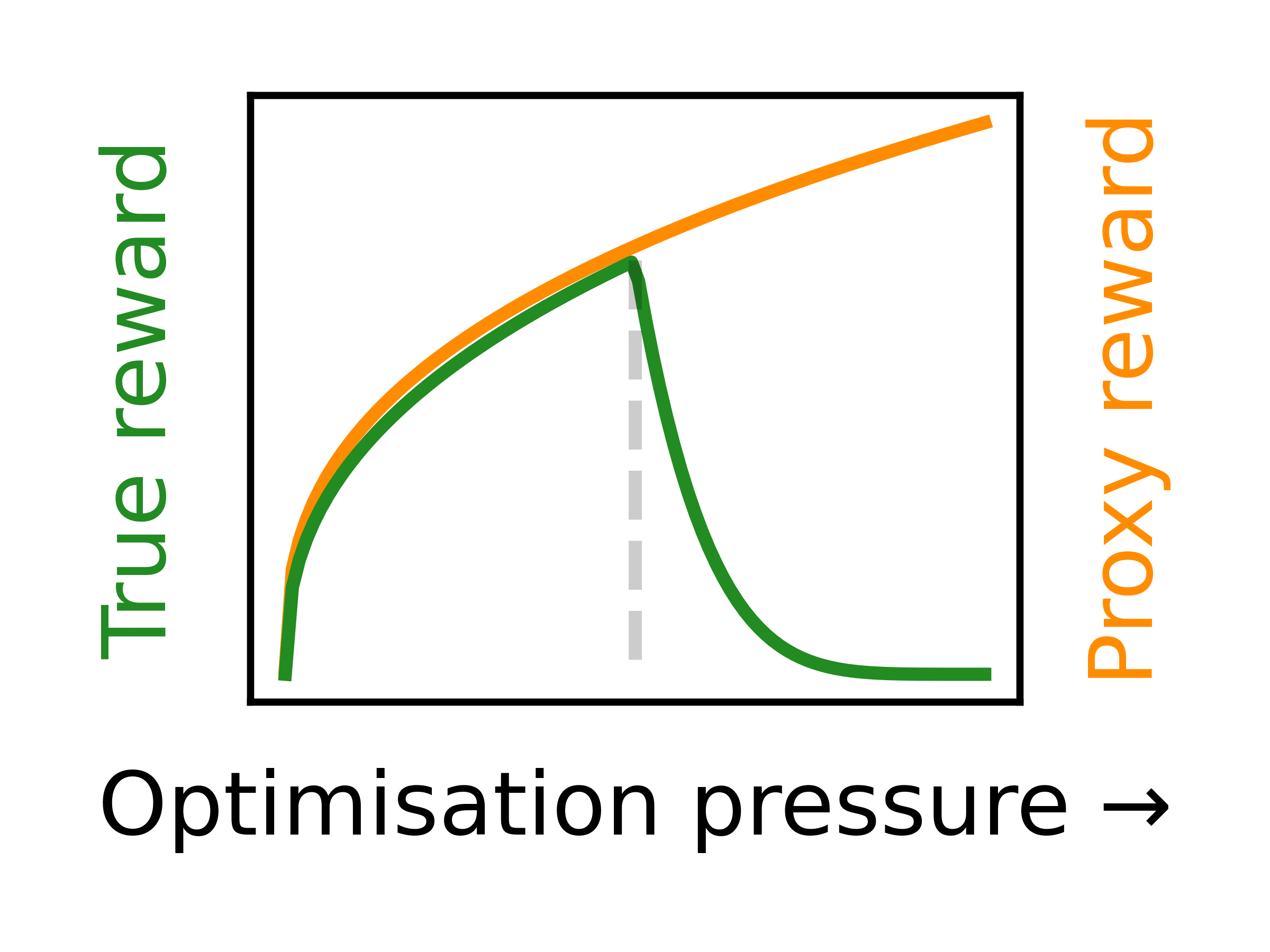
In machine learning, this phenomenon has been studied before. We have a long list lot of examples where agents discover surprising ways of getting reward without increasing their true performance. These examples, however, have not necessarily been quantified over increasing optimisation pressure: we only know that agents discovered those "reward hacks" at some point in their training. Even in cases where the effect was attributed specifically to the increasing optimisation pressure, we lacked a true, mechanistic understanding for why it happens.
Our paper fills this gap. The core contribution is an explanation for Goodhart's law in reinforcement learning in terms of the geometry of Markov decision processes. We use this theoretical insight to develop new methods for provably avoiding Goodharting and for optimising reward under uncertainty. We also show empirically that Goodharting occurs quite often in many different MDPs and investigate the performance of our early-stopping method (which, being pessimistic, might usually lose on some reward).
Geometric explanation
Suppose that we work with a fixed MDP, with states, actions (we assume both being finite) and a discount factor . We are interested in the space of (Markov) policies giving, for every state , a probability distribution over actions. For every reward we can compute the expected return for any policy . Unfortunately, the function can be quite complex. However, it turns out that instead of working with policies, we might instead choose to work with state-action occupancy measures. There is an occupancy measure for each policy : it is defined over pairs (state , action ), and indicates roughly how often we take action in state . Formally:
but the exact form is not really needed to understand the explanation below.
The state-action occupancy measure space has a number of extremely nice properties:
- We can recover a policy from its occupancy measure (up to the states that were never visited).
- The space of occupancy measures is a convex hull over a finite number of points, corresponding to occupancy measures of deterministic policies.
- Moreover, lies in the affine subspace of dimension (we will denote the orthogonal projection matrix to that subspace by ).
- If we treat rewards on MDPs as vectors , then the RL cost function can be decomposed as . In other words, each reward induces a linear function on the convex polytope , which reduces finding the optimal policy to solving a linear programming problem in !
In short: the space of policies over a MDP can be understood as a certain polytope , where for a given reward , finding optimal policy for is really solving a linear program. Or, putting it differently, the gradient of is a linear function in the polytope.
We can visualise it as follows:
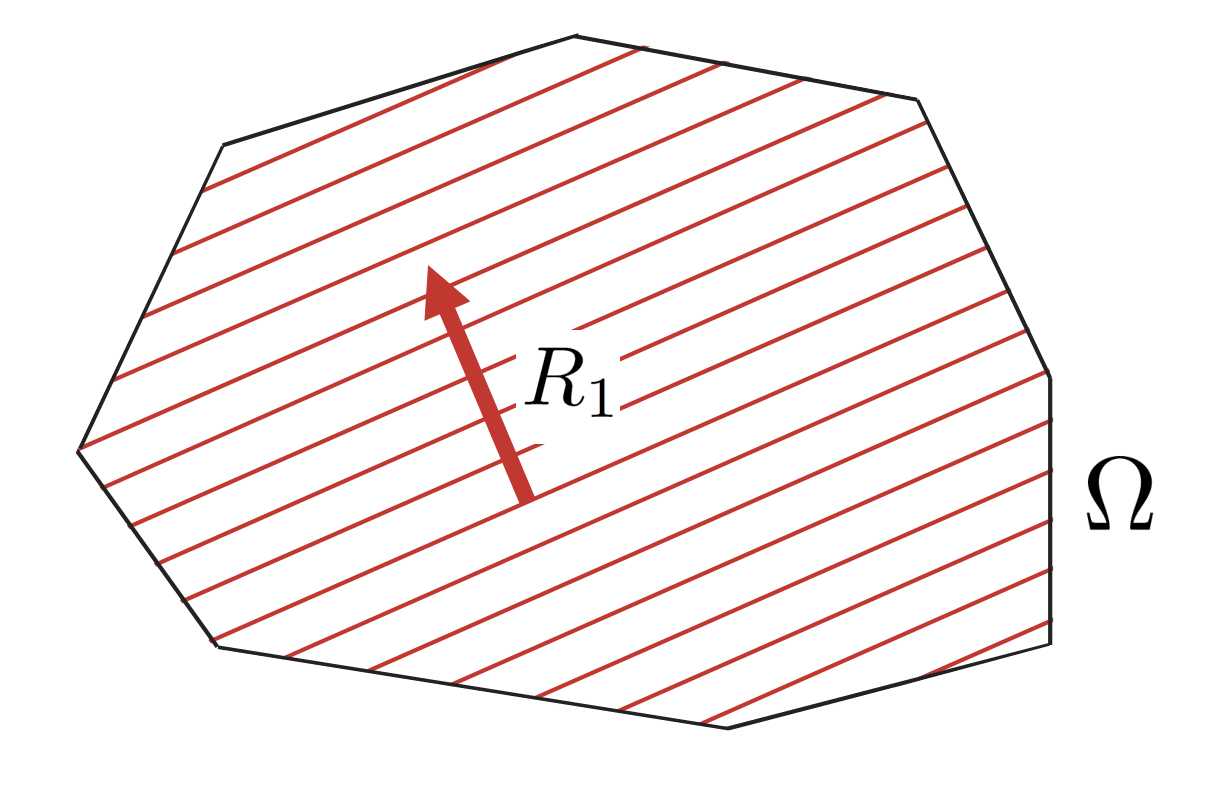
Here the red arrow denotes the direction of within . Note that this direction corresponds to , rather than , since lies in a lower-dimensional affine subspace. Similarly, the red lines correspond to the level sets of , i.e. the directions we can move in without changing .
Now, if is a proxy reward, then we may assume that there is also some (unknown) true reward function . This reward also induces a linear function on , and the angle between them is :
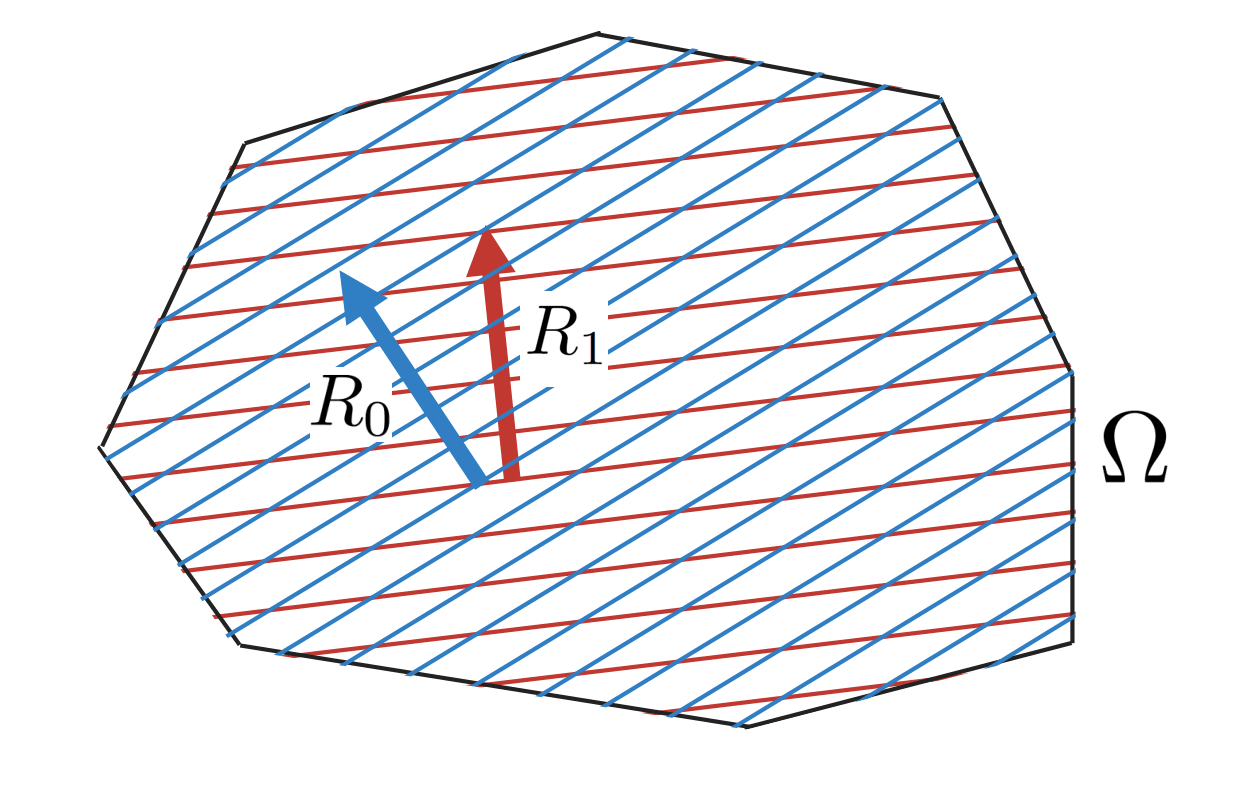
Suppose we pick a random point in , and then move in a direction that increases . This corresponds to picking a random policy , and then modifying it in a direction that increases . In particular, let us consider what happens to the true reward function , as we move in the direction that most rapidly increases the proxy reward .
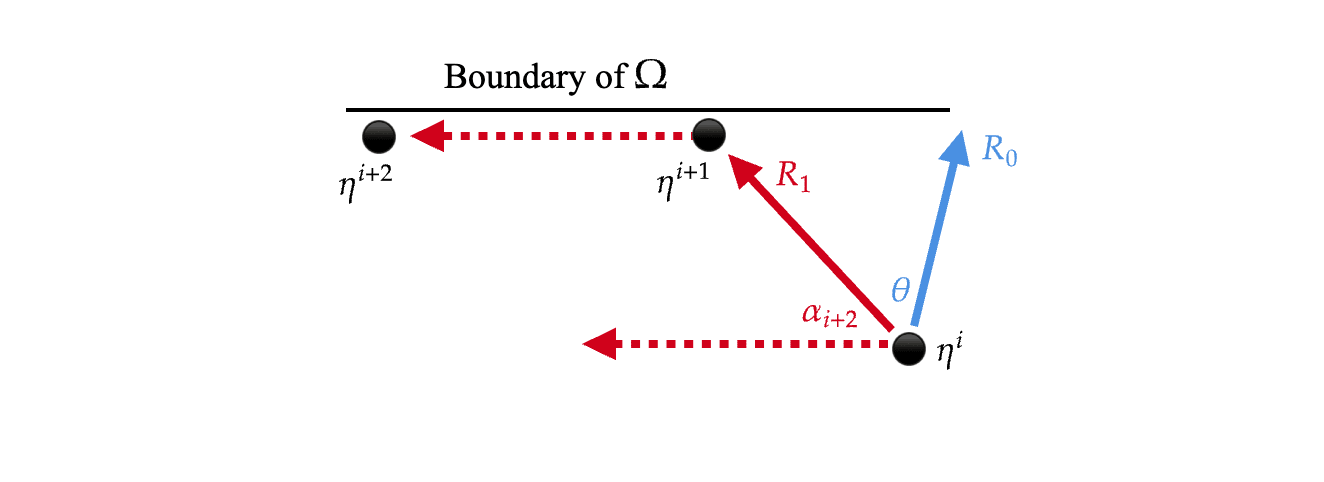
To start with, if we are in the interior of (i.e., not close to any constraints), then the direction that most rapidly increases is to move parallel to . Moreover, if the angle between and is no more than , then this is guaranteed to also increase the value of . To see this, consider the following diagram:
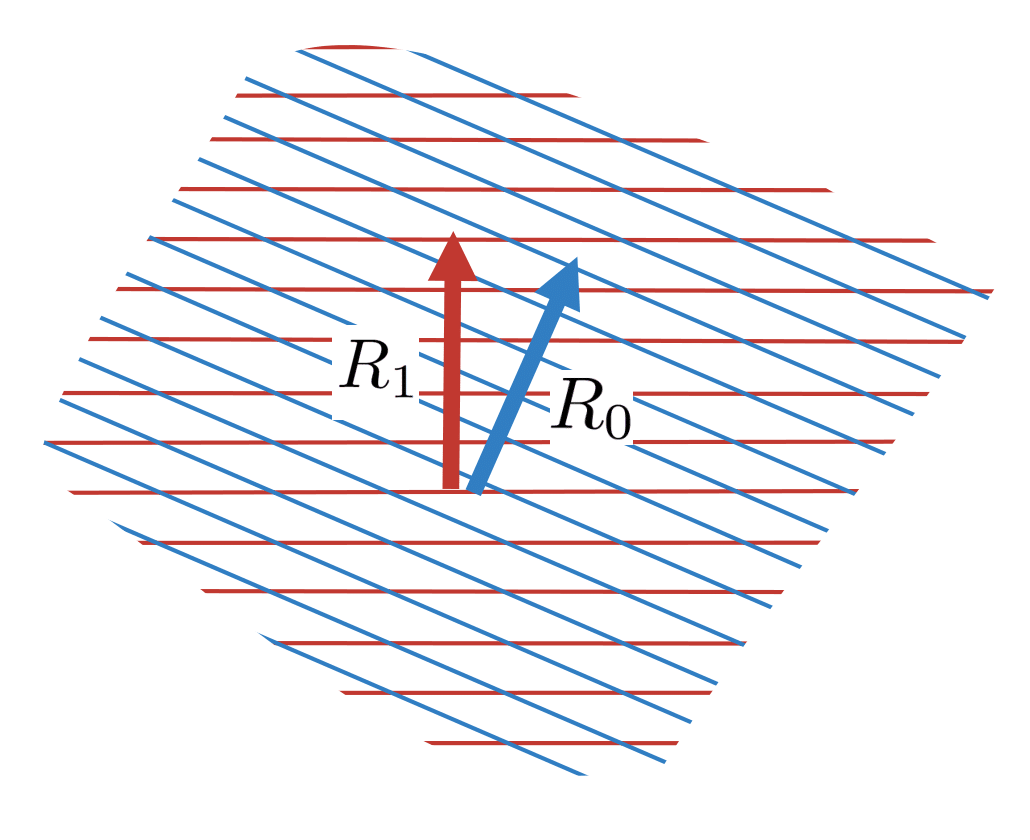
However, as we move parallel to , we will eventually hit the boundary of . When we do this, the direction that most rapidly increases will no longer be parallel to . Instead, it will be parallel to the projection of onto the boundary of that we just hit. Moreover, if we keep moving in this direction, then we might no longer be increasing the true reward . To see this, consider the following diagram:
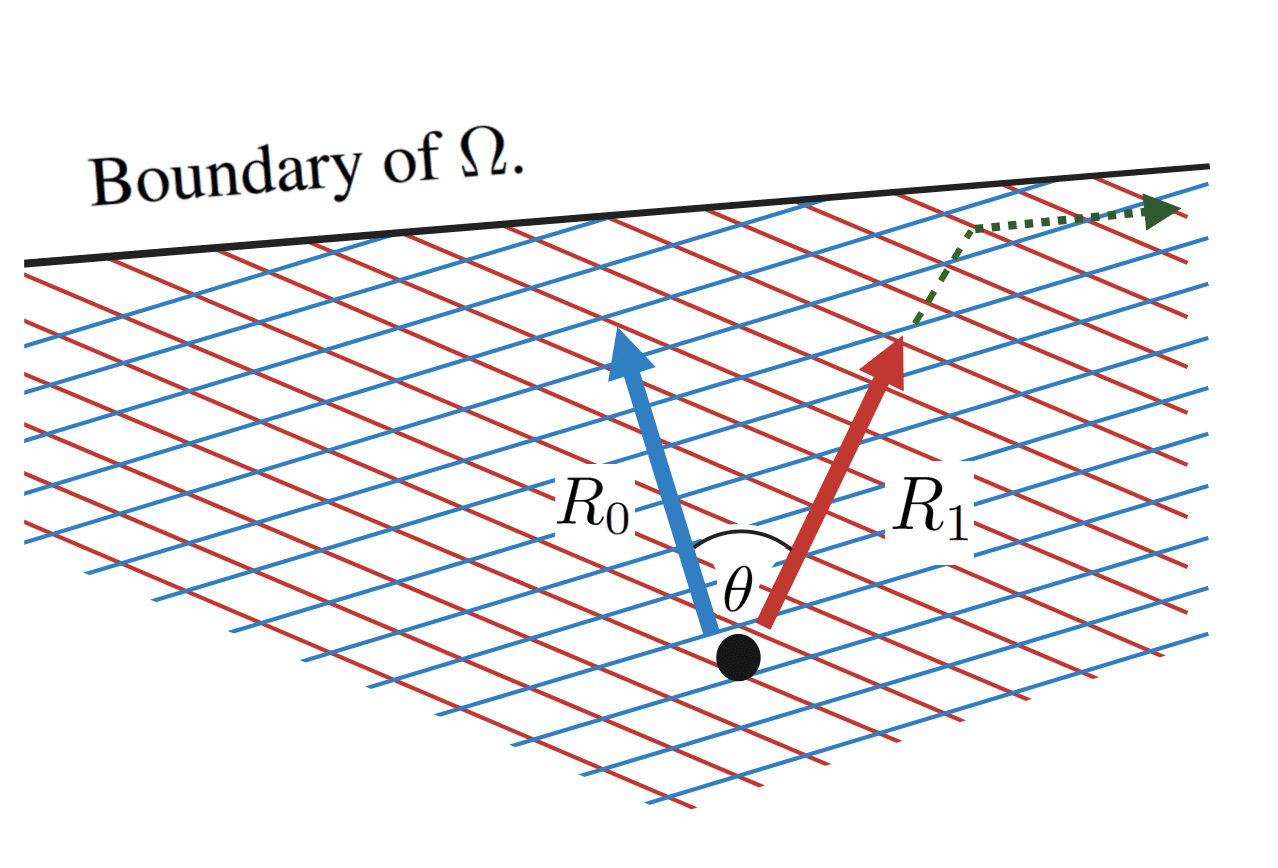
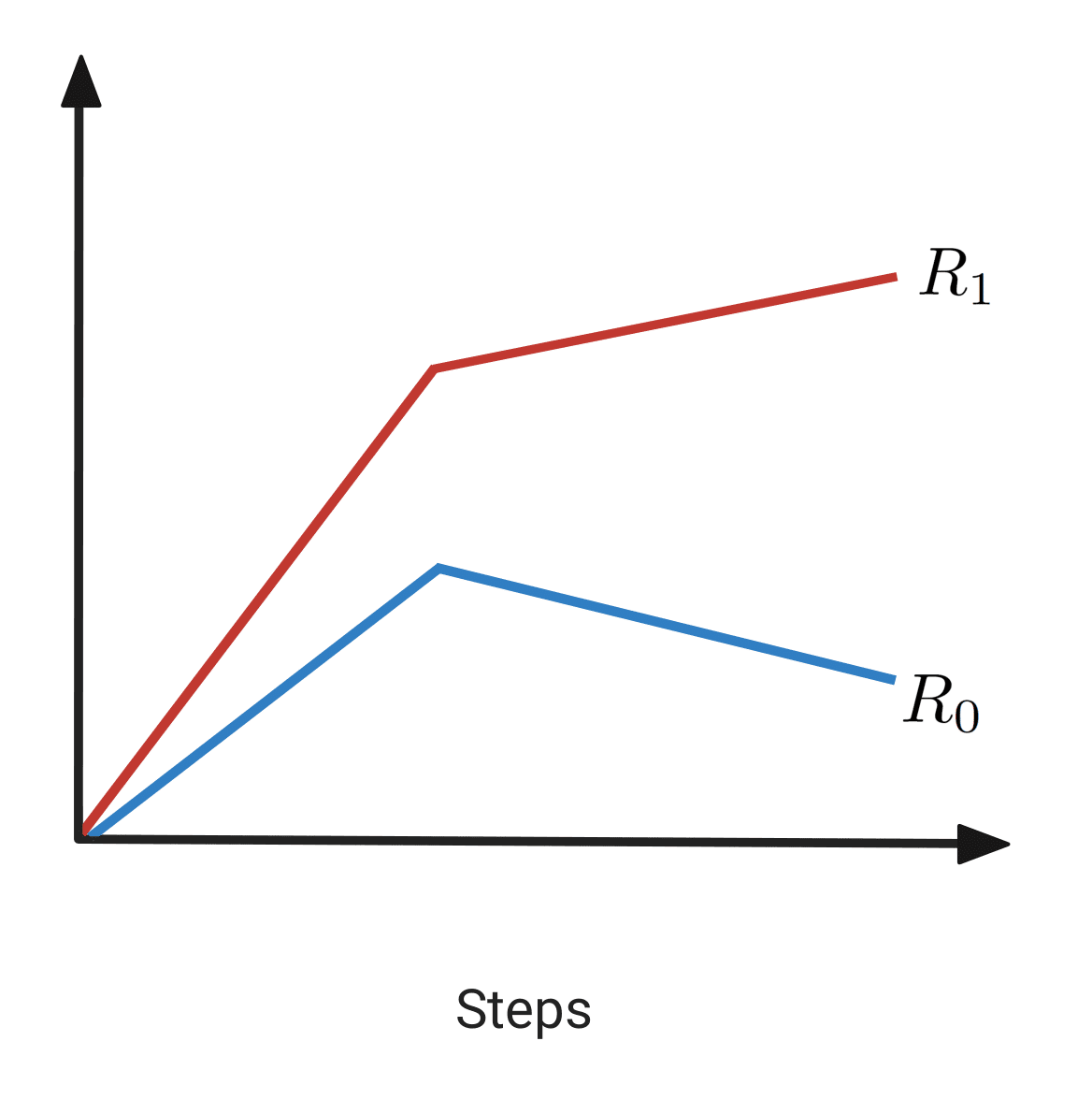
The dashed green line corresponds to the path that most rapidly increases . As we move along this path, initially increases. However, after the path hits the boundary of and changes direction, will instead start to decrease. Thus, if we were to plot and over time, we would get a plot that looks roughly like this:
Next, it is important to note that is not guaranteed to decrease after we hit the boundary of . To see this, consider the following diagram:
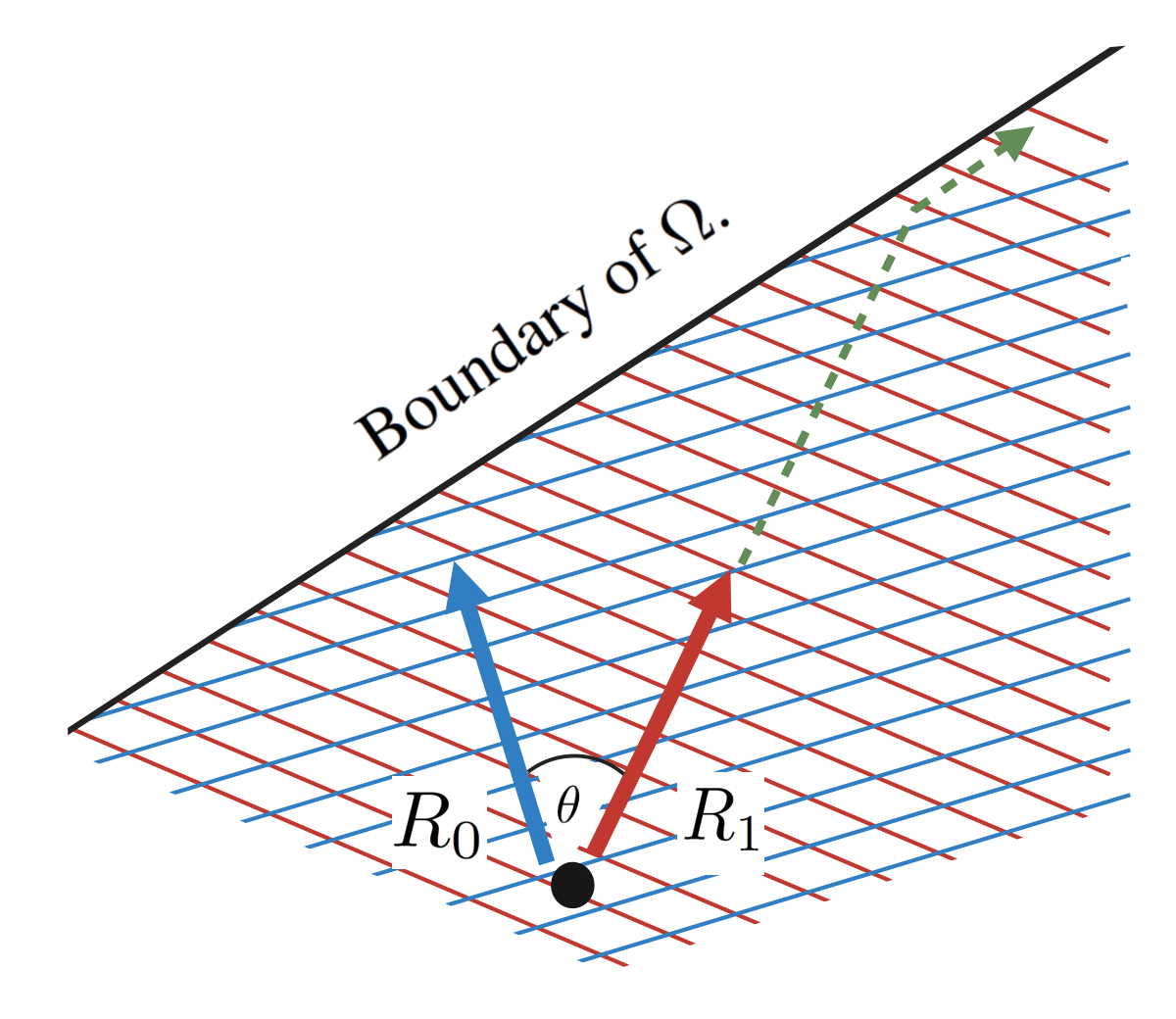
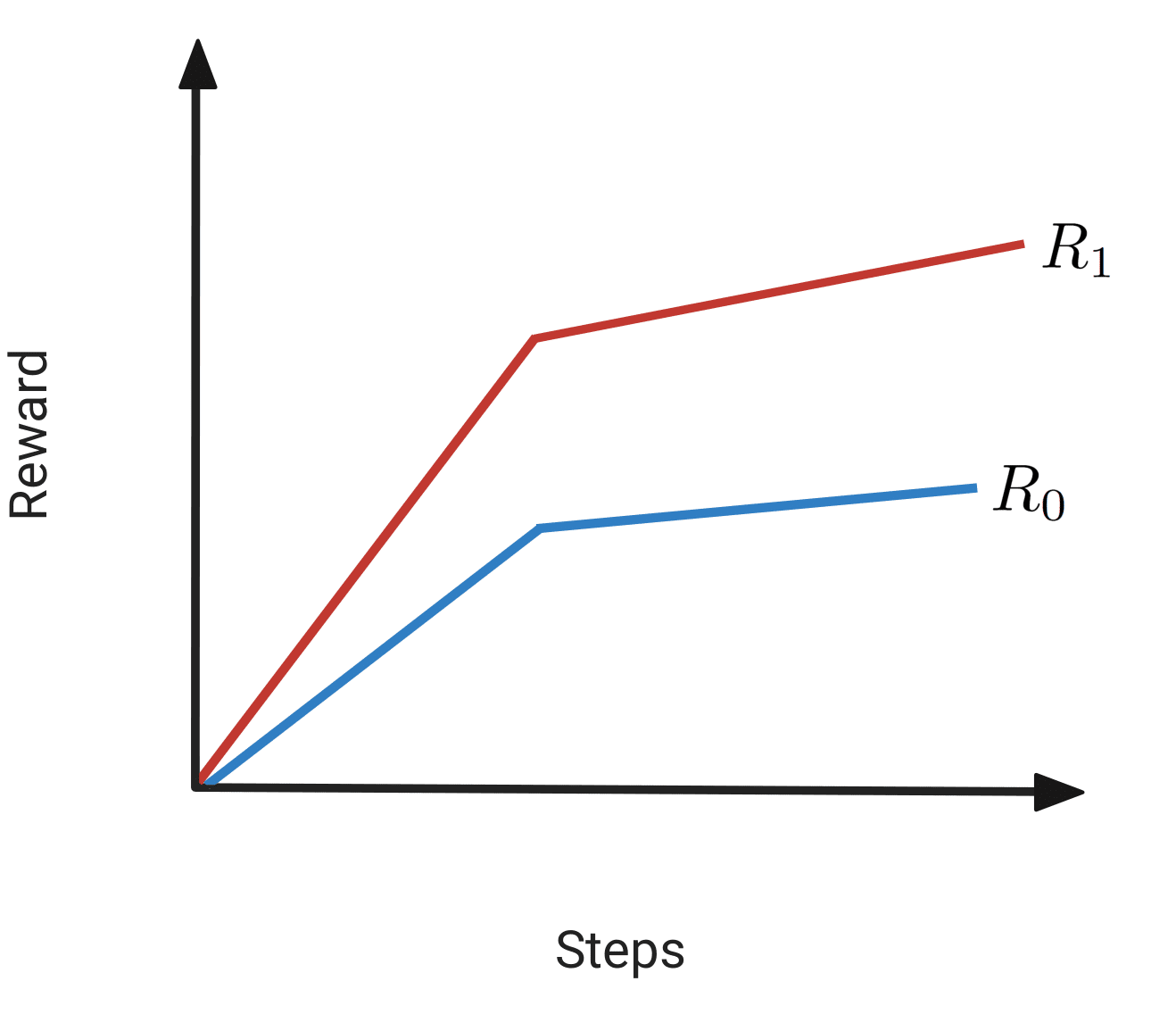
The dashed green line again corresponds to the path that most rapidly increases . As we move along this path, will increase both before and after the path has hit the boundary of . If we were to plot and over time, we would get a plot that looks roughly like this:
The next thing to note is that we will not just hit the boundary of once. If we pick a random point in , and keep moving in the direction that most rapidly increases until we have found the maximal value of in , then we will hit the boundary of over and over again. Each time we hit this boundary we will change the direction that we are moving in, and each time this happens, there is a risk that we will start moving in a direction that decreases .
Goodharting corresponds to the case where we follow a path through along which initially increases, but eventually starts to decrease. As we have seen, this must be caused by the boundaries of .
We may now ask; under what conditions do these boundaries force the path of steepest ascent (of ) to move in a direction that decreases ? By inspecting the above diagrams, we can see that this depends on the angle between the normal vector of that boundary and , and the angle between and . In particular, in order for to start decreasing, it has to be the case that the angle between and is larger than the angle between and the normal vector of the boundary of . This immediately tells us that if the angle between and is small, then Goodharting will be less likely to occur.
Moreover, as the angle between and the normal vector of the boundary of becomes smaller, Goodharting should be correspondingly more likely to occur. In our paper, Proposition 3 tells us that this angle will decrease monotonically along the path of steepest ascent (of ). As such, Goodharting will get more and more likely the further we move along the path of steepest ascent. This explains why Goodharting becomes more likely when more optimisation pressure is applied.
How can we use this intuition?
Preventing Goodharting is difficult because we only have access to the proxy reward. If we only observe , we don't know whether we are in the situation on the left or the situation on the right:
However, we might detect that there is a danger of Goodharting: if we have a bound on the angle between the true and the proxy, then we can detect when there is at least one policy within a cone of around whose return goes down. This is the idea for the pessimistic early stopping algorithm we have developed. Specifically, we track the current direction of optimisation relative to the proxy reward given by , in the occupancy measure space:
If , or equivalently, , there is a possibility of Goodharting - since pessimistically, we are moving opposite to some possible true reward .
In the interior of the polytope , we know that the increase in return is given by the product of how much we moved and the magnitude of the (projected) reward vector: . In general, it has to be rescaled by the current direction of optimisation: .
Therefore, assuming that the LHS of the following inequality is non-increasing (Proposition 3 in the paper again):
we can simply stop first that satisfies it. This is the optimal (last possible) point where we still provably avoid Goodharting.
What's next?
Early-stopping can, unfortunately, lose out on quite a lot of reward, so we think this particular method can be best used in situations where it is much more important to prevent Goodharting than to get good performance in absolute terms. It is also expensive to compute the occupancy measure and the angle . Still, the algorithm can be improved in many directions: for example, we might be able to construct a training algorithm where we alternate between (1) training a model and (2) collecting more data about the reward function. In this way, we collect just enough information for training to proceed, without ever falling into Goodharting. We write about some of those possibilities in the paper but leave the details for future work.
So here's a thing that I think John is pointing at, with a bit more math?:
The diversion is in the distance function.
- In the paper, we define the distance between rewards as the angle between reward vectors.
- So what we sort of do is look at the "dot product", i.E., look at E[R1(S,A)⋅R2(S,A)] for true and proxy rewards R1 and R2 with states/actions sampled according to a uniform distribution. I give justification as to why this is a natural way to define distance in a separate comment.
But the issue here is that this isn't the distribution of the actions/states we might see in practice. E[R1(S,A)⋅R2(S,A)] might be very high if states/actions are instead weighted by drawing them from a distribution induced from a certain policy (e.g., the policy of "killing lots of snakes without doing anything sneaky to game the reward" in the examples, I think?). But then as people optimize, the policy changes and this number goes down. A uniform distribution is actually likely quite far from any state/action distributions we would see in practice.
In other words the way we formally define reward distance here will often not match how "close" two reward functions seem, and lots of cases of "Goodharting" are cases where two reward functions just seem close on a particular state/action distribution but aren't close according to our distance metric.
This makes the results of the paper primarily useful for working towards training regimes where we optimize the proxy and can approximate distance, which is described in Appendix F of the paper. This is because as we optimize the proxy it will start to generalize, and then problems with over-optimization as described in the paper are going to start mattering a lot more.