This post examines an attempt by professional decision theorists to treat an example of time inconsistency, and asks why they failed to reach the solution (i.e., TDT/UDT) that this community has more or less converged upon. (Another aim is to introduce this example, which some of us may not be familiar with.) Before I begin, I should note that I don't think "people are crazy, the world is mad" (as Eliezer puts it) is a good explanation. Maybe people are crazy, but unless we can understand how and why people are crazy (or to put it more diplomatically, "make mistakes"), how can we know that we're not being crazy in the same way or making the same kind of mistakes?
The problem of the ‘‘absent-minded driver’’ was introduced by Michele Piccione and Ariel Rubinstein in their 1997 paper "On the Interpretation of Decision Problems with Imperfect Recall". But I'm going to use "The Absent-Minded Driver" by Robert J. Aumann, Sergiu Hart, and Motty Perry instead, since it's shorter and more straightforward. (Notice that the authors of this paper worked for a place called Center for the Study of Rationality, and one of them won a Nobel Prize in Economics for his work on game theory. I really don't think we want to call these people "crazy".)
Here's the problem description:
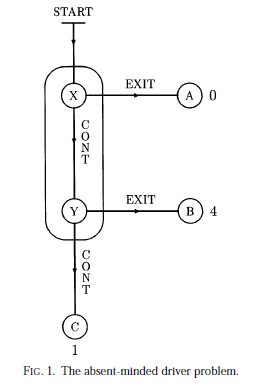
An absent-minded driver starts driving at START in Figure 1. At X he
can either EXIT and get to A (for a payoff of 0) or CONTINUE to Y. At Y he
can either EXIT and get to B (payoff 4), or CONTINUE to C (payoff 1). The
essential assumption is that he cannot distinguish between intersections X
and Y, and cannot remember whether he has already gone through one of
them.
At START, the problem seems very simple. If p is the probability of choosing CONTINUE at each intersection, then the expected payoff is p2+4(1-p)p, which is maximized at p = 2/3. Aumann et al. call this the planning-optimal decision.
The puzzle, as Piccione and Rubinstein saw it, is that once you are at an intersection, you should think that you have some probability α of being at X, and 1-α of being at Y. Your payoff for choosing CONTINUE with probability p becomes α[p2+4(1-p)p] + (1-α)[p+4(1-p)], which doesn't equal p2+4(1-p)p unless α = 1. So, once you get to an intersection, you'd choose a p that's different from the p you thought optimal at START.
Aumann et al. reject this reasoning and instead suggest a notion of action-optimality, which they argue should govern decision making at the intersections. I'm going to skip explaining its definition and how it works (read section 4 of the paper if you want to find out), and go straight to listing some of its relevant properties:
- It still involves a notion of "probability of being at X".
- It's conceptually more complicated than planning-optimality.
- Mathematically, it has the same first-order necessary conditions as planning-optimality, but different sufficient conditions.
- If mixed strategies are allowed, any choice that is planning-optimal is also action-optimal.
- A choice that is action-optimal isn't necessarily planning-optimal. (In other words, there can be several action-optimal choices, only one of which is planning-optimal.)
- If we are restricted to pure strategies (i.e., p has to be either 0 or 1) then the set of action-optimal choices in this example is empty, even though there is still a planning-optimal one (namely p=1).
In problems like this one, UDT is essentially equivalent to planning-optimality. So why did the authors propose and argue for action-optimality despite its downsides (see 2, 5, and 6 above), instead of the alternative solution of simply remembering or recomputing the planning-optimal decision at each intersection and carrying it out?
Well, the authors don't say (they never bothered to argue against it), but I'm going to venture some guesses:
- That solution is too simple and obvious, and you can't publish a paper arguing for it.
- It disregards "the probability of being at X", which intuitively ought to play a role.
- The authors were trying to figure out what is rational for human beings, and that solution seems too alien for us to accept and/or put into practice.
- The authors were not thinking in terms of an AI, which can modify itself to use whatever decision theory it wants to.
- Aumann is known for his work in game theory. The action-optimality solution looks particularly game-theory like, and perhaps appeared more natural than it really is because of his specialized knowledge base.
- The authors were trying to solve one particular case of time inconsistency. They didn't have all known instances of time/dynamic/reflective inconsistencies/paradoxes/puzzles laid out in front of them, to be solved in one fell swoop.
Taken together, these guesses perhaps suffice to explain the behavior of these professional rationalists, without needing to hypothesize that they are "crazy". Indeed, many of us are probably still not fully convinced by UDT for one or more of the above reasons.
EDIT: Here's the solution to this problem in UDT1. We start by representing the scenario using a world program:
def P(i, j):
if S(i) == "EXIT":
payoff = 0
elif S(j) == "EXIT":
payoff = 4
else:
payoff = 1
(Here we assumed that mixed strategies are allowed, so S gets a random string as input. Get rid of i and j if we want to model a situation where only pure strategies are allowed.) Then S computes that payoff at the end of P, averaged over all possible i and j, is maximized by returning "EXIT" for 1/3 of its possible inputs, and does that.

S() is suppose to be an implementation of UDT. By looking at the world program P, it should determine that among all possible input-output mappings, those that return "EXIT" for 1/3 of all inputs (doesn't matter which ones) maximize average payoff. What made me express the payoff as a function of p is by stepping through what S is supposed to do as an implementation of UDT.
Does that make sense?
I'm still confused. Your response seems to just say, "I did it because it works." -- which is a great reason! But I want to know if UDT gave you more guidance than that.
Does UDT require that you look at the consequences of doing something p% of the time (irrespective of which ones), on all problems?
Basically, I'm in the position of that guy/gal that everyone here probably helped out in high school:
"How do you do the proof in problem 29?" "Oh, just used identities 3 and 5, solve for t, and plug it back into the original equation." "But how did you know to do that?"