The archetypal example for this is something like a thermostat. The variable S represents random external temperature fluctuations. The regulator R is the thermostat, which measures these fluctuations and takes an action (such as putting on heating or air conditioning) based on the information it takes in. The outcome Z is the resulting temperature of the room, which depends both on the action taken by the regulator, and the external temperature.
The ordinary room thermostat does not measure S. It measures Z. Its actions are determined by Z and the reference temperature set by the user (in your example assumed constant and omitted for simplicity). There is no causal arrow from S to R. Here is the true causal diagram:

The room thermostat is therefore outside the scope of the GRT. This is true of every control system that senses the variable it is controlling, i.e. every control system.
The diagram is a causal Bayes net which is a DAG so it can't contain cycles. Your diagram contains a cycle between R and Z. The diagram I had in mind when writing the post was something like:
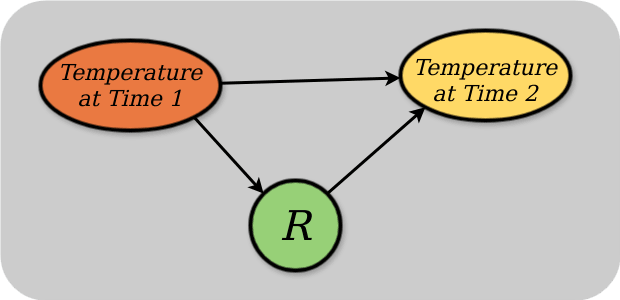
which is a thermostat over a single timestep.
If you wanted to have a feedback loop over multiple timesteps, you could conjoin several of these diagrams:
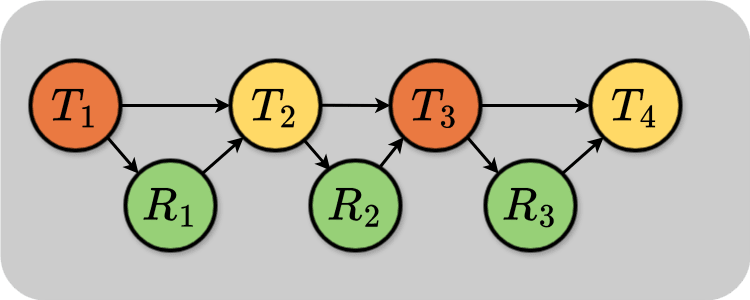
Each node along the top row is the temperature at successive times. Each node along the bottom row is the controller state at different times.
The diagram is a causal Bayes net which is a DAG so it can't contain cycles. Your diagram contains a cycle between R and Z.
Indeed. So much the worse for causal Bayes nets. People have tried to extend Pearl-type causal analysis to cyclic causal graphs, but have not got very far. The limits of our tools are not the limits of the world.
I am not convinced by the idea of unrolling the graph in time. Outside of digital electronics, time is continuous [1]. There is no time step for the room thermostat. For more complicated systems, the causal relationships you see when you discretise time may vary depending on the chosen time step. Continuous time and differential equations are the right abstraction.
It would not be helpful to bring up speculations about the ultimately discrete nature of space-time on the Planck scale. ↩︎
The unrolled loop still should not have the arrow between S and R, and should have the feedback, because the controller is sensing the outcome. Unrolled it should go: S1 -> Z1, R1->Z1, Z1 -> R2, R2 -> Z2, S2-> Z2 ...
How do you figure a thermostat directly measures what it's controlling? It controls heat added/removed per unit time, typically just more/less/no change, and measures the resulting temperature at a single point on typically a minute+ delay due to the dynamics of the system (air and heat take time to diffuse, even with a blower). Any time step sufficiently shorter than that delay is going to work the same. The current measurement depends on what the thermostat did tens of seconds if not minutes previously.
There are times the continuous/discrete distinction is very important but this example isn't one of them. As soon as you introduce a significant delay between cause and effect the time step model works (it may well be a dependence on multiple previous time-steps, but not the current one).
I don't think this is an unusual example, we have a small number of sensors, we get data on a delay, and we're actually trying to control e.g. the temperature in the whole house, holding a set point, minimizing variation between rooms and minimizing variation across time, with the smallest amount of control authority over the system (typically just on/off).
I believe "sufficiently shorter than the delay" is just going to be Nyquist Shannon sampling theorem, once you're sampling twice the frequency of the highest frequency dynamic in the system, your control system has all the information from the sensor and sampling more will not tell you anything else.
This is partly a terminology issue. By "controlling a variable" I mean "taking actions as necessary to keep that variable at some reference level." So I say that the thermostat is controlling the temperature of the room (or if you want to split hairs, the temperature of the temperature sensor—suitably siting that sensor is an important part of a practical system). In the same sense, the body controls its core temperature, its blood oxygenation level, its posture[1], and many other things, and its actions to obtain those ends include sweating, breathing, changing muscle tensions, etc.
By the "output" or "action" of a control system I mean the actions it takes to keep the controlled variable at the reference. For the thermostat, this is turning the heat source on and off. It is not "controlling" (in the sense I defined) the rate of adding heat. The thermostat does not know how much heat is being delivered, and does not need to.
The resulting behaviour of the system is to keep the temperature of the room between two closely spaced levels: the temperature at which it turns the heat on, and the slightly higher temperature at which it turns the heat off. The rate at which the temperature goes up or down does not matter, provided the heat source is powerful enough to replenish all the energy leaking out of the walls, however cold it gets outside. If the heat source were replaced by one delivering twice as much power, the performance of the thermostat would be unchanged, except for being able to cope with more extreme cold weather.
The only delays in the thermostat itself are the time it takes for a mechanical switch to operate (milliseconds) and the time it takes for heat production to reach the sensor (minutes). These are so much faster than the changes in temperature due to the weather outside that it is most simply treated as operating in continuous time. There would be no practical benefit from sampling the temperature discretely and seeing how slow a sample rate you can get away with.
How do we manage not to fall over? To walk and run? These are deep questions. ↩︎
It sounded previously like you were making the strong claim that this setup can't be applied to a closed control loop at all, even in e.g. the common (approximately universal?) case where we have a delay between the regulator's action and it's being able to measure that action's effect. That's mostly what I was responding to; the chaining that Alfred suggested in the sibling comment seems sensible enough to me.
It occurs to me that the household thermostat example is so non-demanding as to not be a poor intuition pump. I implicitly made the jump to thinking about a more demanding version of this without spelling that out. It's always going to be a little silly trying to optimize an example that's already intuitively good enough. Imagine for sake of argument a apparatus that needs tighter control such that there's actually pressure to optimize beyond the simplest control algorithm.
Your examples of control systems all seem fine and accurate. I think we agree the tricky bit is picking the most sensible frame for mapping the real system to the diagram (assuming that's roughly what you mean by terminology).
It seems like even with the improvements John Wentworth suggests there's still some ambiguity in how to apply the result to a case where the regulator makes a time series of decisions, and you're suggesting there's some reason we can't, or wouldn't want to use discrete timesteps and chain/repeat the diagram.
At a little more length, I'm picturing the unrolling such that the current state is the sensor's measurement time series through present, of which the regulator is certain. It's merely uncertain about how its action - what fraction of the next interval to run the heat - will effect the measurement at future times. It's probably easiest if we draw the diagram such that the time step is the delay between action and measured effect, and the regulator then sees the result of its action based on T1 at T3.
That seems pretty clearly to me to match the pattern this theorem requires, while still having a clear place to plug in whatever predictive model the regulator has. I bring up the sampling theorem as that is the bridge between the discrete samples we have and the continuous functions and differential equations you elsewhere say you want to use. Or stated a little more broadly, that theorem says we can freely move between continuous and discrete representations as needed, provided we sample frequently enough and the functions are well enough behaved to be amenable to calculus in the first place.
(I have been busy, hence the delay.)
It sounded previously like you were making the strong claim that this setup can't be applied to a closed control loop at all, even in e.g. the common (approximately universal?) case where we have a delay between the regulator's action and it's being able to measure that action's effect.
I am making that claim. Closed loops have circular causal links between the (time-varying) variables. The SZR diagram that I originally objected to is acyclic, therefore it does not apply to closed loops.
Loop delays are beside the point. Sampling on that time scale is not required and may just degrade performance.
Imagine for sake of argument a apparatus that needs tighter control such that there's actually pressure to optimize beyond the simplest control algorithm.
You are assuming that that tighter control demands the sort of more complicated algorithms that you are imagining, that predict how much heat to inject, based on a model of the whole environment, and so on.
Let's look outward at the real world. All you need for precision temperature control is to replace the bang-bang control with a PID controller and a scheme for automatically tuning the PID parameters, and there you are. There is nothing in the manual for the ThermoClamp device to suggest a scheme of your suggested sort. In particular, like the room thermostat, the only thing it senses is the actual temperature. Nothing else. For this it uses a thermocouple, which is a continuous-time device, not sampled. There is also no sign of any model. I don't know how this particular device tunes its PID parameters (probably a trade secret), but googling for how to auto-tune a PID has not turned up anything suggesting a model, only injecting test signals and adjusting the parameters to optimise observed performance -- observed solely through measuring the controlled variable.
The early automatic pilots were analogue devices operating in continuous time.
Everything is digital these days, but a modern automatic pilot is still sampling the sensors many times a second, and I'm sure that's also true of the digital parts of the ThermoClamp. The time step is well below the characteristic timescales of the system being controlled. It has to be.
People talk about eliminating the cycles by unrolling. I believe this does not work. In causal graphs as generally understood, each of the variables is time-varying. In the unrolled version, each of the nodes represents the value of a single variable at a single point in time, so it's a different sort of thing. Unrolling makes the number of nodes indefinitely large, so how are you going to mathematically talk about it? Only by taking advantage of its repetitive nature, and then you're back to dealing with cyclic causal graphs while pretending you aren't. "Tell me you're using cyclic causal graphs without telling me you're using cyclic causal graphs."
(I have been busy, hence the delay.)
No worries, likewise.
Most centrally I think we're seeing fundamentally different things with the causal graph. Or more to the point, I haven't the slightest idea how one is supposed to do any useful reasoning with time varying nodes without somehow expanding it to consider how one node's function and/or time series effects it's leaf nodes (or another way, specifically what temporal relation the arrow represents). It also seems fairly inescapable to me that any way you consider that relation, an actual causal cycle where A causes B causes C causes A at the same instant looks very different than one where they indirectly effect each-other at some later time, to the point of needing different tools to analyze the two cases. The latter looks very much like the sort of thing solved with recursion or update loops in programs all the time. Alternately diff eq in the continuous case. The former looks like the sort of thing you need a solver to look for a valid solution for.
It's fairly obvious why cycles of the first kind I describe would need different treatment - the graph would place constraints on valid solutions but not tell you how to find them. I'm not seeing how the second case is cyclic in the same sense and how you couldn't just use induction arguments to extend to infinity.
AFAICT you and I aren't disagreeing on anything about real control systems. It's difficult to find a non-contrived example because so many control systems either aren't that demanding or have a human in the loop. But this theorem is about optimal control systems, optimal in the formal computer science sense, so the fact that neither of us can come up with an example that isn't solved by a PID control loop or similar is somewhat besides the point.
While PID controllers are applicable to many control problems and often perform satisfactorily without any improvements or only coarse tuning, they can perform poorly in some applications and do not in general provide optimal control.
Although it’s true that the GRT is not applicable to a thermostat, there are a very wide class of controllers which do not measure their outcomes.
The first example that comes to mind would be a position controller for a robot which uses only wheel odometry to estimate the current position. The robot doesn't actually measure its position (the control outcome), but rather estimates it from wheel travel by assuming some model of traction.
In that situation the robot is controlling estimated position, not real position. If the estimate is always accurate then the distinction will not matter, but if not, and especially if it accumulates a drift, it will.
I believe you are looking for the distinction between closed loop and open loop controllers. IIUC this theorem only applies to open loop controllers. OP's flowchart does not contain a feedback loop. For comparison, Richard Kennaway's flowchart has a feedback loop between Z and R.
An example of an open loop controller is a dishwasher or laundry machine.
All animals are examples of closed loop controllers.
I consider "open loop control" almost a contradiction in terms. I mean, I don't have anything to quarrel with in the Wikipedia article, but it's not an effective way to actually control anything, unless there's a closed-loop controller wrapped around it. (Often this takes the form of a human being inspecting and adjusting the equipment.) One might as well call the screws holding a piece of furniture together an open-loop controller.
Perhaps I'm off on this but wanted to just ask. How much of that term being a contradiction is driven by the lack of a good underlying model of something. I'll use the house temperature example here.
We have a very good model (by assumption here) of energy transmission from the exterior to the interior. We have a controller (thermostat) that only measures external features, say outside temp and maybe light and a time duration for when and how long to run either the air conditioner or heating. With a good model (and probably a good initialization at installation) that regulator seems like it would do a good job of hitting the defined internal temp target without needing to monitor the internal temp.
That certainly fails the GRT on the grounds it's a lot more complicated than it needs to be as measuring the internal temp and then activating the AC or heating is pretty simple and straightforward. But having a good model seems to fit well with the Shannon entropy aspects - the model itself tells us what is needed about the internal temp so monitoring/sampling that variable is not necessary.
Is the complicated regulation no an open loop control case? Or is it still something of a contradiction in terms in your view?
With a good model
There's the rub. Your model will have to not only know the external temperature, but also the conductivity of the walls, the power delivered or extracted by the heat/cold source, the people or pet animals in the room and how much heat they are generating, the temperature in the adjoining rooms, and all the other factors affecting the temperature that the designer may not have thought of.
All to avoid the cost of a thermometer which you'll need anyway to calibrate the model. This is Heath Robinson, not practical engineering.
Thank you for writing this! Your description in the beginning about trying to read about the GRT and coming across a sequence of resources, each of which didn't do quite what you wanted, is a precise description of the path I also followed. I gave up at the end, wishing that someone would write an explainer, and you have written exactly the explainer that I wanted!
Curated. Simple straightforward explanations of notable concepts is among my favorite genre of posts. Just a really great service when a person, confused about something, goes on a quest to figure it out and then shares the result with others. Given how misleading the title of the theorem is, it's valuable here to have it clarified. Something that is surprising, is given what this theorem actual says and how limited it is, that it's the basic of much other work given what it purportedly states, but perhaps people are assuming that the spirit of it is valid and it's saved by modifications that e.g. John Wentworth provides. It'd be neat to see more of analysis of that. It'd be sad if a lot of work cites this theorem because people believed the claim of the title without checking the proof really supports it. All in all, kudos for making progress on all this.
This may be the most misleading title and summary I have ever seen on a math paper. If by “making a model” one means the sort of thing people usually do when model-making - i.e. reconstruct a system’s variables/parameters/structure from some information about them - then Conant & Ashby’s claim is simply false. - John Wentworh
If a regulator is 'good' (in the sense described by the two criteria in the previous section), then the variable R can be described as a deterministic function of S .
Really! This is the theorem?
Is there anyone else who understands the Good Regulator Theorem that can confirm this?
The reasons I'm surprised/confused are:
- This has nothing to do with modelling
- The teorem is too obviously true to be interesting
johnswentworth's post Fixing The Good Regulator Theorem has the same definition of the Good Regulator Theorem.
That is enough for me to confirm that this is indeed what it says. Not because I trust John more than Alfred, but because there are now tow independent enough claims on LW for the same definition of the theorem, which would be very surprising if the definition was wrong.
I know you asked for other people (presumably not me) to confirm this but I can point you to the statement of the theorem, as written by Conant and Ashby in the original paper :
Theorem: The simplest optimal regulator R of a reguland S produces events R which are related to the events S by a mapping
Restated somewhat less rigorously, the theorem says that the best regulator of a system is one which is a model of that system in the sense that the regulator’s actions are merely the system’s actions as seen through a mapping h.
I agree that it has nothing to do with modelling and is not very interesting! But the simple theorem is surrounded by so much mysticism (both in the paper and in discussions about it) that it is often not obvious what the theorem actually says.
I took a college course in probability theory but never took one on information theory that would have given a formal definition of Shannon entropy, so I guess I'm a little bit underqualified for this explanation? I think I can kind of handwave my way through it, though, with the general idea that the lowest entropy a "random" variable can have is when it's constant...
It is meant to read 350°F. The point is that the temperature is too high to be a useful domestic thermostat. I have changed the sentence to make this clear (and added a ° symbol ). The passage now reads:
Scholten gives the evocative example of a thermostat which steers the temperature of a room to 350°F with a probability close to certainty. The entropy of the final distribution over room temperatures would be very low, so in this sense the regulator is still 'good', even though the temperature it achieves is too high for it to be useful as a domestic thermostat.
(Edit: I've just realised that 35°F would also be inappropriate for a domestic thermostat by virtue of being too cold so either works for the purpose of the example. Scholten does use 350, so I've stuck with that. Sorry, I'm unfamiliar with Fahrenheit!)
::looks up Farenheit the person on Wikipedia::
Apparently, Daniel Farenheit was the inventor of the mercury thermometer (a significant improvement over the liquor-filled thermometers of the era), and his original procedure for calibrating it defined three points on a temperature scale: a solution of ammonium chloride in ice water should be zero degrees, the freezing point of water should be 30 degrees, and human body temperature should be 90 degrees. (That last one was a bit off - holding the other two points constant, it should have been 95.)
People soon noticed that there were very close to 180 degrees between the melting and boiling points of water, so the scale was changed a bit to redefine the freezing and boiling points of water to be exactly 180 degrees apart. In the current version of the Farenheit scale, the boiling point of water is 212 degrees, the freezing point of water is 32 degrees, and the standard value for human body temperature is 98.6 degrees. It's not an elegant system, but by coincidence it does happen to be a pretty good scale for outdoor temperatures, which tend to range between 0 and 100 degrees (instead of between -20 and 40 degrees on the Celsius scale.).
350 degrees Farenheit, incidentally, happens to be a common temperature for baking food in an oven. 😆
Really enjoyed this post, thank you for making the original theorem so much more digestible!
I’m still learning to think in this formal direction, so I wanted to test my understanding by applying it to a domain I know well: legal AI governance in the EU.
Here’s the framing I tried:
- R (Regulator) = The European Commission, AI Office, and adjacent regulatory bodies tasked with steering AI development, risk mitigation, and commercialisation through laws and standards.
- S (System) = The entire AI development landscape affecting Europe—including global developments, given the Brussels effect and the extraterritorial pull of EU regulations.
- Z (Outcome) = The observable effects on society, markets, and risk distribution from AI systems (same as in the original formulation).
I’m currently researching how foundational AI safety concepts can be adapted for regulatory design in the EU context. So this is mostly an exercise to train my brain, not a new claim.
Some of this may look misguided to those more familiar with the theorem, very happy to be corrected!!
---
The Problem with Perfect Knowledge of S
In this setup, it’s immediately clear that R (the EU regulator) cannot meet the assumption of perfect knowledge of S. In fact, its information about the state of AI development is often:
- Partial (relying on self-assessments and opaque model disclosures),
- Lagging (laws are drafted over years, breakthroughs happen monthly), and
- Politically filtered (due to industrial policy, lobbying, and differing risk appetites across member states).
The theorem assumes that R can deterministically respond to S. But if S is the global AI ecosystem, then this is not just untrue, but structurally impossible.
What Can Be Done?
Regulators can't minimize entropy in Z if they lack observability into S. The legal process is deterministic by design, but the system it tries to regulate (S) is non-deterministic, high-velocity, and partially adversarial.
The best R can do is build probabilistic regulators: laws and procedures designed for bounded uncertainty rather than perfect foresight.
This might involve:
- Scalable oversight institutions (analogous to alignment's scalable supervision),
- Simulated models or red-team stress tests to explore likely behaviors of S under different policy levers,
- Periodic re-anchoring of regulatory frameworks to model drift and emerging capabilities (though the current legislative cycle struggles to keep up).
It seems to me that unless institutional capacity is built to approximate S more closely, entropy in Z is baked in, and the Regulator is more likely than not to always fail the basic standard of being “good” in the Conant/Ashby sense.
Curious to hear if this sort of mapping holds water. I realize it’s informal and a bit hand-wavy, but I’m trying to think more rigorously about why legal regimes struggle to govern advanced AI systems, and this theorem felt like a useful test case.
Would appreciate any pushback or corrections from those with stronger formal grounding.
Shannon entropy
Some examples of what the formula produces:
Fair coin is 2 (sides) x .5 (probability) x log(2) = 1 x .3010 = .3
Fair hundred sided die 100 x .01 x log(100) = 1 x 2 = 2
Where the Good Regulator Theorem breaks down isn't in whether or not people understand it. Consensus agreement with the theorem is easy to assess. The theorem itself does not have to be. That is, if one believes that in-group consensus among experts is the greatest indicator of truth, then as long as the consensus of experts agrees that the Good Regulator Theorem is valid, everyone else can simply evaluate whether the consensus supports the theorem, rather than evaluating the theorem itself. In reality, this is what most people do most of the time. For example, many people believe in the possibility of the big bang. Of those people, how many can deduce their reasoning from first principles vs how many simply rely on what the consensus of experts say is true? I would wager that the number who can actually justify their reasoning is vanishingly small.
Instead, where the theorem breaks down is in being misapplied. The Good Regulator Theorem states: “Every good regulator of a system must contain a model of that system.” This seems straightforward until you try to apply it to AI alignment, at which point everything hinges on two usually implicit assumptions: (1) what the "system" is, and (2) what counts as a "model" of it. Alignment discourse can often collapse at one of these two junctions, usually without noticing.
1. First Assumption: What Kind of Model Are We Talking About?
The default move in a lot of alignment writing is to treat “a model of human values” as something that could, in principle, be encoded in a fixed list of goals, constraints, or utility function axioms. This might work in a narrow, closed domain—say, aligning a robot arm to not smash the beaker. But real-world human environments are not closed. They're open, dynamic, generative, and full of edge cases humans haven’t encountered yet, and where their values aren’t just hard to define—they’re under active construction.
Trying to model human values with a closed axiom set in this kind of domain is like trying to write down the rules of language learning before you've invented language. It’s not just brittle—it’s structurally incapable of adapting to novel inputs. A more accurate model needs to capture how humans generate, adapt, and re-prioritize values based on context. That means modeling the function of intelligence itself, not just the outputs of that function. In other words, when applied to AI alignment, the Good Regulator Theorem implies that alignment requires a functional model of intelligence—because the system being regulated includes the open-ended dynamics of human cognition, behavior, and values.
2. Second Assumption: What Is the System Being Regulated?
Here’s the second failure point: What exactly is the AI regulating? The obvious answer is “itself”—that is, the AI is trying to keep its own outputs aligned with human goals. That’s fine as far as it goes. But once you build systems that act in the world, they’re not just regulating themselves anymore. They're taking actions that affect humans and society. So in practice, the AI ends up functioning as a regulator of human-relevant outcomes—and by extension, of humans themselves.
The difference matters. If the AI’s internal model is aimed at adjusting its own behavior, that’s one kind of alignment problem. If its model is aimed at managing humans to achieve certain ends, that’s a very different kind of system, and it comes with a much higher risk of manipulation, overreach, or coercion—especially if the designers don't realize they’ve shifted frames.
The Core Problem
So here’s the bottom line: Even if you invoke the Good Regulator Theorem, you can still end up building something misaligned if you misunderstand what the AI is regulating or what it means to “contain a model” of us.
- If you assume values are static and encodable, you get brittle optimization.
- If you misidentify the system being regulated, you might accidentally build a coercive manager instead of a corrigible assistant.
The Good Regulator Theorem doesn’t solve alignment for you. But it does make one thing non-negotiable: whatever system you think you’re regulating, you’d better be modeling it correctly. If you get that part wrong, everything else collapses downstream.
This post was written during the agent foundations fellowship with Alex Altair funded by the LTFF. Thanks to Alex, Jose, Daniel, Cole, and Einar for reading and commenting on a draft.
The Good Regulator Theorem, as published by Conant and Ashby in their 1970 paper (cited over 1700 times!) claims to show that 'every good regulator of a system must be a model of that system', though it is a subject of debate as to whether this is actually what the paper shows. It is a fairly simple mathematical result which is worth knowing about for people who care about agent foundations and selection theorems. You might have heard about the Good Regulator Theorem in the context of John Wentworth's 'Gooder Regulator' theorem and his other improvements on the result.
Unfortunately, the original 1970 paper is notoriously unfriendly to readers. It makes misleading claims, doesn't clearly state what exactly it shows and uses strange non-standard notation and cybernetics jargon ('coenetic variables' anyone?). If you want to understand the theorem without reading the paper, there are a few options. John Wentworth's post has a nice high-level summary but refers to the original paper for the proof. John Baez's blogpost is quite good but is very much written in the spirit of trying to work out what the paper is saying, rather than explaining it intuitively. I couldn't find an explanation in any control theory textbooks (admittedly my search was not exhaustive). A five year-old stackexchange question, asking for a rigorous proof, goes unanswered. The best explainer I could find was Daniel L. Scholten's 'A Primer for Conant and Ashby's Good-Regulator Theorem' from the mysterious, now-defunct 'GoodRegulatorProject.org' (link to archived website). This primer is nice, but really verbose (44 pages!). It is also aimed at approximately high-school (?) level, spending the first 15 pages explaining the concept of 'mappings' and conditional probability.
Partly to test my understanding of the theorem and partly to attempt to fill this gap in the market for a medium-length, entry-level explainer of the original Good Regulator Theorem, I decided to write this post.
Despite all the criticism, the actual result is pretty neat and the math is not complicated. If you have a very basic familiarity with Shannon entropy and conditional probability, you should be able to understand the Good Regulator Theorem.
This post will just discuss the original Good Regulator Theorem, not any of John Wentworth's additions. I'll also leave aside discussion of how to interpret the theorem (questions such as 'what counts as a model?' etc.) and just focus on what is (as far as I can tell) the main mathematical result in the paper.
Let's begin!
The Setup
Conant and Ashby's paper studies a setup which can be visualised using the following causal Bayes net:
If you are not familiar with Bayes nets you can just think of the arrows as meaning 'affects'. So A→B means 'variable A affects the outcome of variable B'. This way of thinking isn't perfect or rigorous, but it does the job.
Just to be confusing , the paper discusses a couple of different setups and draws a few different diagrams, but you can ignore them. This is the setup they study and prove things about. This is the only setup we will use in this post.
The broad idea of a setup like this is that the outcome Z is affected by a system variable S and a regulator variable R. The system variable is random. The regulator variable might be random and independent of S but most of the time we are interested in cases where it depends on the value of S. By changing the way that R depends on S, the distribution over outcomes Z can be changed. As control theorists who wish to impose our will on the uncooperative universe, we are interested in the problem of 'how do we design a regulator which can steer Z towards an outcome we desire, in spite of the randomness introduced by S?'
The archetypal example for this is something like a thermostat. The variable S represents random external temperature fluctuations. The regulator R is the thermostat, which measures these fluctuations and takes an action (such as putting on heating or air conditioning) based on the information it takes in. The outcome Z is the resulting temperature of the room, which depends both on the action taken by the regulator, and the external temperature.
Each node in the Bayes net is a random variable. The 'system' is represented by a random variable S, which can take values from the set {s1,s2,...sdS}. It takes these values with probabilities P(s1),P(s2) etc. Think of the system as an 'environment' which contains randomness.
The variable R represents a 'regulator'- a random variable which can take values from the set {r1,r2,...rdR}. As the diagram above shows, the regulator can be affected by the system state and is therefore described by a conditional probability distribution P(R|S). Conditional probabilities tell you what the probability of R is, given that S has taken a particular value. For example, the equation P(R=r2|S=s5)=0.9 tells us that if S takes the value s5, then the probability that R takes the value r2 is 0.9. When we discuss making a good regulator, we are primarily concerned with choosing the right conditional probability distribution P(R|S) which helps us achieve our goals (more on exactly what constitutes 'goals' in the next section). One important assumption made in the paper is that the regulator has perfect information about the system, so R can 'see' exactly what value S takes. This is one of the assumptions which is relaxed by John Wentworth, but since we are discussing the original proof, we will keep this assumption for now.
Finally, the variable Z represents the 'outcome' - a random variable which can take values from the set {z1,z2,...zdZ}. The variable Z is entirely determined by the values of R and S so we can write it as a deterministic function of the regulator state and the system state. Following Conant and Ashby, we use ψ to represent this function, allowing us to write Z=ψ(R,S). Note that it is possible to imagine cases where Z is related to R and S in a non-deterministic way but Conant and Ashby do not consider cases like this so we will ignore them here (this is another one of the extensions proved by John Wentworth - I hope to write about these at a later date!).
What makes a regulator 'good'?
Conant and Ashby are interested in the question: 'what properties should R have in order for a regulator to be good?' In particular, we are interested in what properties the conditional probability distribution P(R|S) should have, so that R is effective at steering Z towards states that we want.
One way that a regulator can be good is if the Shannon entropy of the random variable Z is low. The Shannon entropy is given by
H(Z)=∑iP(Z=zi)log1P(Z=zi).The Shannon entropy tells us how 'spread out' the distribution on Z is. A good regulator will make H(Z) as small as possible, steering Z towards a low-uncertainty probability distribution. Often, in practice, a producing a low entropy outcome is not on its own sufficient for a regulator to be useful. Scholten gives the evocative example of a thermostat which steers the temperature of a room to 350°F with a probability close to certainty. The entropy of the final distribution over room temperatures would be very low, so in this sense the regulator is still 'good', even though the temperature it achieves is too high for it to be useful as a domestic thermostat. Going forward, we will use low outcome entropy as a criterion for a good regulator, but its better to think of this as a necessary and/or desirable condition rather than sufficient condition for a good regulator.
The second criterion for a good regulator, according to Conant and Ashby, is that the regulator is not 'unnecessarily complex'. What they mean by this is that if two regulators achieve the same output entropy, but one of the regulators uses a policy involving some randomness and the other policy is deterministic, the policy that uses randomness is unnecessarily complex, so is less 'good' than the deterministic policy.
For example, imagine we have a setup where ψ(r1,s2)=ψ(r2,s2)=z1. Then, when the regulator is presented with system state s2, it could choose from between the following policies:
All three of these policies achieve the same result (the outcome will always be z1 whenever S=s2), and the same output entropy, but the third option is 'unnecessarily complex', so is not a good regulator. Argue amongst yourselves about whether you find this criterion convincing. Nonetheless, it is the criterion Conant and Ashby use, so we will use it as well.
To recap: a good regulator is one which satisfies the following criteria:
The Theorem Statement
The theorem statement can be written as follows:
If a regulator is 'good' (in the sense described by the two criteria in the previous section), then the variable R can be described as a deterministic function of S .
Another way of saying that 'R can be described as a deterministic function of S' is to say that for every ri and sj, then P(R=ri|S=sj) either equals 0 or 1. This means that R can be written as R=f(S) for some mapping f.
We are now almost ready the prove the theorem. But first, it is worth introducing a basic concept about entropy, from which the rest of the Good Regulator Theorem flows straightforwardly.
Concavity of Entropy
Conant and Ashby write:
This is probably pretty intuitive if you are familiar with Shannon Entropy. Here is what it means. Suppose we have a probability distribution P(Z) which assigns probabilities P(Z=za) and P(Z=zb) for two different outcomes with P(Z=za)≥P(Z=zb) (and other probabilities to other z-values). Now suppose we increase the probability of outcome za (which was already as likely or more likely than zb) and decrease P(Z=zb) the same amount while keeping the rest of the distribution the same. The resulting distribution will end up with a lower entropy than the original distribution. If you are happy with this claim you can skip the rest of this section and move on to the next section. If you are unsure, this section will provide a little more clarification of this idea.
One way to prove this property is to explicitly calculate the entropy of a general distribution where one of the probabilities is pa+δ and another is pb−δ (where pa≥pb and δ>0) . Then, you can differentiate the expression for entropy with respect to δ and show that dHdδ<0 ie. H is a decreasing function of δ. This is fine and do-able if you don't mind doing a little calculus. Scholten has a nice walk-through of this approach in the section of his primer titled 'A Useful and Fundamental Property of the Entropy Function'.
Here is another way to think about it. Consider a random variable Z′ with only two outcomes za and zb. Outcome za occurs with probability q and zb occurs with probability 1−q. The entropy of this variable is
H(Z′)=qlog1q+(1−q)log11−q.This is a concave function of q. When plotted (using base 2 logarithms) it looks like this:
If q≤0.5, decreasing q decreases the entropy and if q≥0.5, increasing q decreases the entropy. So 'increasing the imbalance' of a 2-outcome probability distribution will always decrease entropy. Is this still true if we increase the imbalance between two outcomes within a larger probabilities distribution with more outcomes? The answer is yes.
Suppose our outcomes za and zb are situated within a larger probability distribution. We can view this larger probability distribution as a mixture of our 2-outcome variable Z′ and another variable which we can call Y which captures all other outcomes. We can write Z (which we can think of as the 'total' random variable) as
Z=λZ′+(1−λ)Y.With probability λ=P(Z=za)+P(Z=zb), the variable Z takes a value determined by Z′ and with probability 1−λ, the value of Z is determined by random variable Y.
It turns out the entropy of such variable, generated by mixing non-overlapping random variables, can be expressed as follows:
H(Z)=λH(Z′)+(1−λ)H(Y)+g(λ)where g(λ)=λlog1λ+(1−λ)log11−λ is the binary entropy (see eg. this Stackexchange answer for a derivation). Increasing the relative 'imbalance' of P(Z=za) and P(Z=zb) while keeping their sum constant does not change λ or H(Y), but does reduce H(Z′), thus reducing the total entropy H(Z).
This is a fairly basic property of entropy but understanding it is one of the only conceptual pre-requisites for understanding the good regulator theorem. Hopefully it is clear now if it wasn't before.
On to the main event!
The Main Lemma
Conant and Ashby's proof consists of one lemma and one theorem. In this section we will discuss the lemma. I'm going to state the lemma in a way that makes sense to me and is (I'm pretty sure) equivalent to the lemma in the paper.
Lemma:
Suppose a regulator is 'good' in the sense that it leads to Z having the lowest possible entropy. Then P(R|S) must have been chosen so that Z is a deterministic function of S ie. H(Z|S)=0.
Here is an alternative phrasing, closer to what Conant and Ashby write:
Suppose a regulator is 'good' in the sense that it leads to Z having the lowest possible entropy. Suppose also that, for a system state sj, this regulator has a non-zero probability of producing states ri and rk, ie. P(R=ri|S=sj)>0 and P(R=rk|S=sj)>0. Then, it must be the case that ψ(ri,sj)=ψ(rk,sj), otherwise, the regulator would not be producing the lowest possible output entropy.
Here is another alternative phrasing:
Suppose a regulator is 'good' in the sense that it leads to Z having the lowest possible entropy. If, for a given system state, multiple regulator states have non-zero probability, then all of these regulator states lead to the same output state when combined with that system state through ψ. If this was not the case, we could find another regulator which lead to Z having a lower entropy.
This is one of those claims which is kind of awkward to state in words but is pretty intuitive once you understand what it's getting at.
Imagine there is a regulator which, when presented with a system state sj, produces state ri with probability P(R=ri|S=sj)≠0 and produces state rk with probability P(R=rk|S=sj)≠0. Furthermore, suppose that ψ is such that ψ(ri,sj)=za and ψ(rk,sj)=zb. This means that, when presented with system state sj, the regulator sometimes acts such that it produces an outcome state za and other times acts so as to produce an outcome state zb. This means Z is not a deterministic function of S. Is it possible that this regulator produces the lowest possible output entropy? From considering the previous section, you might already be able to see that the answer is no, but I'll spell it out a bit more.
The total probability that Z=za will be given by the sum of the probability that Z=za, when S is not sj and the probability that R is ri when S equals sj:
P(za)=P(Z=za|S≠sj)P(S≠sj)+P(R=ri|S=sj)P(S=sj)Similarly the probably that Z=zb is given by:
P(zb)=P(Z=zb|S≠sj)P(S≠sj)+P(R=rk|S=sj)P(S=sj).Suppose P(za)≥P(zb), then, as we saw in the previous section, we can reduce the entropy of Z by increasing P(za) and decreasing P(zb) by the same amount. This can be achieved by changing the regulator so that P(R=ri|S=sj) is increased and P(R=rk|S=sj) is decreased by the same amount. Therefore, a regulator which with nonzero probability produces two different R values when presented with the same S-value cannot be optimal if those two R-values lead to different Z-values. We can always find a regulator which consistently picks ri 100% of the time which leads to a lower output entropy. (A symmetric argument can be made if we instead assume P(zb)≥P(za) .)
However, if ψ was such that ψ(ri,sj)=ψ(rk,sj)=za, then it would not matter whether the regulator picked ri or rk or tossed a coin to decide between them when presented with sj, because both choices would lead to the same Z-value. In such a case, even though R contains randomness, the overall effect would be that Z is still a deterministic function of S.
The Theorem
90% of the meat of the theorem is contained in the above lemma, we just need to tie up a couple of loose ends. To recap: we have showed that a regulator which achieves the lowest possible output entropy must use a conditional distribution P(R|S) which leads to Z being a deterministic function of S. For each system state sj, the regulator must only choose R-values which lead to a single Z-value. This still leaves open the possibility that the regulator can pick a random R-value from some set of candidates, provided that all of those candidates result in the same Z-value. In our example from the previous section, this would mean that the regulator could toss a coin to choose between ri and rk when presented with system state sj and this regulator could still achieve the minimum possible entropy.
This is where the 'unnecessary complexity' requirement comes in. Conant and Ashby argue that one of the requirements for a 'good' regulator is that it does not contain any unnecessary complexity. A regulator which randomises its R value would be considered unnecessarily complex compared to a regulator which produced the same output state distribution without using randomness. Therefore, for a regulator to be 'good' in the Conant and Ashby sense, it can only pick a single R-value with 100% probability when presented with each S-value. And the main lemma tells us that this condition does not prevent us from minimizing the output entropy.
This means that in the conditional probability distribution P(R|S), for each S-value, the probability of any one R-value is either zero or one. To put it another way, R can be described as a deterministic function of S. In a good regulator, knowing S allows you to predict exactly what value R will take. Also, since Z is a deterministic function of R and S, this means that Z, when being regulated by a good regulator, will be a deterministic function of S.
Thus, we have proved that a good regulator R must be a deterministic function of the system state S.
Note that the argument makes no assumptions about the probability distribution over S. Though changing the probability distribution over S will change the final output entropy, it will not change the properties of a good regulator.
Example
Consider the following example, where R, S, and Z have three possible states and the 'dynamics' function ψ is characterised by the following table:
First, consider a regulator which violates the main condition of the main lemma, by randomizing between r1 and r2 when presented with s1, even though they lead to different Z-values. Here is the conditional probability table for such a regulator:
If S has a maximum entropy distribution so P(s1)=P(s2)=P(s3)=13, then this regulator will produce outcome z1 with probability 56. Outcome z2 will have probability P(z2)=0 and outcome z3 will have P(z3)=16. This output distribution will therefore have entropy
H(Z)=56log65+16log61≈0.65(using base 2 logarithms). According to the lemma, we can achieve a better (lower) output entropy by ensuring that P(R|S) is such that the regulator chooses whichever R-value corresponds to the Z-value which already has a higher probability. In this case, z1 has a higher probability than z3, so 'increasing the imbalance' means increasing the probability of z1, at the expense of z3 as much as we can. This can be done by increasing P(r1|s1) to 1 and decreasing P(r2|s1) to zero (while keeping the rest of the distribution the same).
This results in a Z-distribution with an entropy of zero, since, regardless of the S-value, Z always ends up in state z1. Since this entropy cannot be improved upon and the regulator does not have any unnecessary noise/complexity, the Good Regulator Theorem predicts that this regulator should be a deterministic function of S. Lo and behold, it is! Each S-value gets mapped to exactly one R-value:
Consider another regulator for the same system, as characterised by the following conditional probability table:
Referring back to the table for ψ, we can see that this regulator also achieves an output entropy of zero, even though it randomizes between r2 and r3 when presented with s2. Since ψ(r2,s2)=ψ(r3,s2)=z1, this isn't a problem from the point of view of minimizing entropy, but it is 'unnecessarily complex', so doesn't meet the criteria of a good regulator as Conant and Ashby define it. There are two ways to make this regulator 'good'. We could either make P(r2|s2)=1 and P(r3|s2)=0, making the regulator the same as our previous example, or we could set P(r2|s2)=0 and P(r3|s2)=1.
Both possibilities would be 'good regulators' in the sense that they achieve the minimum possible entropy and are not unnecessarily complex. They are also both regulators where R is a deterministic function of S, validating the prediction of the theorem.
Conclusion
One thing that Conant and Ashby claim about this theorem is that it shows that a good regulator must be 'modelling' the system. This is a bit misleading. As I hope I have shown, the Good Regulator Theorem shows that a good regulator (for a certain definition of 'good') must depend on the system in a particular way. But the way in which a good regulator must depend on the system does not correspond to what we might normally think of as a 'model'. The regulator must have a policy where its state deterministically depends on the system state. That's it! If we were being very generous, we might want to say something like: 'this is a necessary but not sufficient condition for a regulator that does model its environment (when the word model is use in a more normal sense)'. When Conant and Ashby say that a good regulator 'is a model of the system', they might mean that looking at R tells you information about S and in that sense, is a model of S. When R is a deterministic function of S, this is sometimes true (for example when R is a bijective or injective function of S). However, in some setups, the 'good' regulator R might be a deterministic function of S which takes the same value, regardless of the value of S. I don't think its sensible to interpret such a regulator as being a model of S.
Personally, I don't think that it is useful to think about the Good Regulator Theorem as a result about models. It's a pretty neat theorem about random variables and entropy (and that's ok!), but on its own, it doesn't say much about models. As with most things in this post, John Wentworth has discussed how you could modify the theorem to say something about models.
After writing this piece, the good regulator theorem is a lot clearer to me. I hope it is clearer to you as well. Notable by its absence in this post is any discussion of John Wentworth's improvements to the theorem. Time permitting, I hope to cover these at a later date.