I'm generally a fan of "maximize economic surplus and then split the benefits fairly". And I think this approach makes the most sense in contexts where agents are bargaining over a joint action space , where is some object-level decision being made and are side-payments that agents can use to transfer value between them.[1]
An example would be a negotiation between Alice and Bob over how to split a pile of tokens, which Alice can exchange for each, and Bob can exchange for each. The sort of situation where there's a real and interpersonally comparable difference in the value they each derive from their least and most favorite outcome.[2]
In this example is the convex set containing joint utilities for all splits of tokens, and the disagreement point. If we take , the Nash and KS bargaining solutions are for Alice and Bob to each receive tokens. But this is clearly not actually Pareto optimal. Pareto optimality looks like enacting a binding agreement between Alice and Bob that "Bob can have all the tokens, and Alice receives a fair split of the money". And I claim the mistake was in modelling as the full set of feasible options, when in fact the world around us redunds with opportunities to do better.
Side payments introduce important geometric information that alone doesn't convey: the real-world tradeoff between making Alice happier and making Bob happier. Bargaining solutions are rightly designed to ignore how utility functions are shifted and scaled, and when is compact we can standardize each agent's utility into .
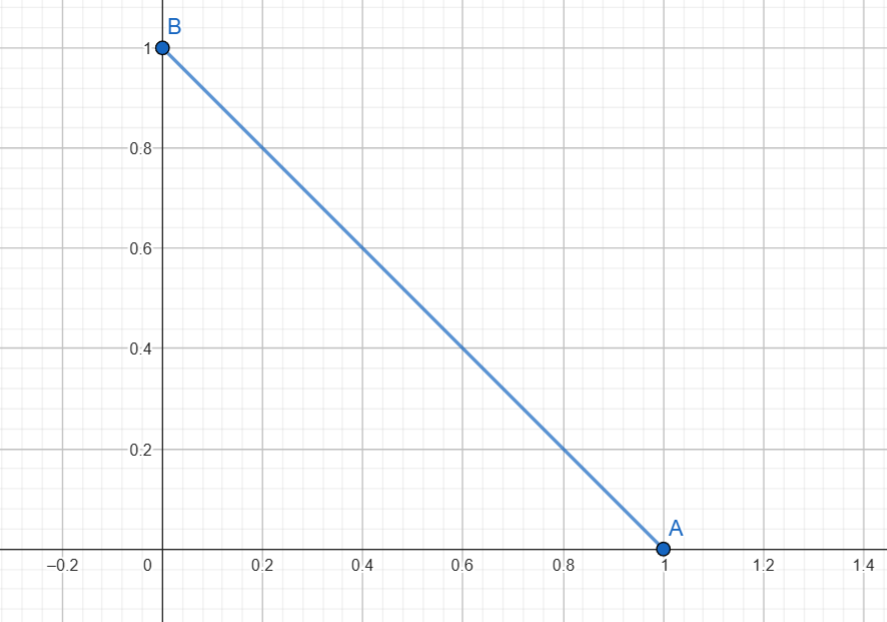
With alone, we can't distinguish between "Bob is just using bigger numbers to measure his utility" (measuring this standardized shape in nano-utilons) and "Bob is actually 1 billion times more sensitive to the difference between his least and most favorite outcome than Alice is."
In this example, when we project the outcome space into standardized joint utility space, the results for and look like that image above: a line sloping down from Bob's favorite outcome to Alice's, and all the space between that line and . And the Nash and KS bargaining solutions will be the same: standardized utilons for each. But when we reverse the projection to find outcomes with this joint utility, for we find ( tokens for Alice, tokens for Bob), and for we find (( tokens for Alice, tokens for Bob), Bob gives Alice ).
Economists call "the resource used to measure value" the numéraire, and usually this unit of caring is money. If we can find or invent a resource that Alice and Bob both value linearly, economists say that they have quasilinear utility functions, which is amazing news. They can use this resource for side payments, it simplifies a lot of calculations, and it also causes agreement among many different ways we might try to measure surplus.
When Alice and Bob each have enough of this resource to pay for any movement across D, then the Pareto frontier of becomes completely flat. And whenever this happens to a Pareto frontier, the Nash and KS bargaining solutions coincide exactly with "maximize economic surplus and split it equally."
"Maximize total utility" and "maximize average utility" are type errors if we interpret them literally. But "maximize economic surplus (and split it fairly)" is something we can do, using tools like trade and side payments to establish a common currency for surplus measurement.
Using Weights as Side Payments
Money is a pretty reasonable type of side-payment, but we could also let agents transfer weights in the joint utility function among themselves. This is the approach Andrew Critch explores in his excellent paper on Negotiable Reinforcement Learning, in which a single RL agent is asked to balance between the interests of multiple principals with different beliefs. The overall agent is an maximizer, where the Harsanyi weights shift according to Bayes rule, giving better predictors more weight in future decisions. The principals essentially bet about the next observation the RL agent will make, where the stakes are denominated in .
One direction Andrew points towards for future work is using some kind of bargaining among sub-agents to determine what the overall agent does. One way to model this is by swapping out maximization for maximization, defining each agent's baseline if no trade takes place, and enriching to include side payments.
- ^
This can also be framed as picking a point on the Pareto frontier, and then letting agents pay each other for small shifts from there. Bargaining over combines these into a single step.
- ^
How do I know utilities can be compared? Exactly because when Bob offers Alice for one of her tokens, she says "yep that sounds good to me!" Money is the unit of caring.
I think modeling utility functions as private information makes a lot of sense! One of the claims I’m making in this post is that utility valuations can be elicited and therefore compared.
My go-to example of an honest mechanism is a second-price auction, which we know we can implement from within the universe. The bids serve as a credible signal of valuation, and if everyone follows their incentives they’ll bid honestly. The person that values the item the most is declared the winner, and economic surplus is maximized.
(Assuming some background facts, which aren't always true in practice, like everyone having enough money to express their preferences through bids. I used tokens in this example so that “willingness to pay” and “ability to pay” can always line up.)
We use the same technique when we talk about the gains from trade, which I think the Ultimatum game is intended to model. If a merchant values a shirt at $5, and I value it at $15, then there's $10 of surplus to be split if we can agree on a price in that range.
Bob values the tokens more than Alice does. We can tell because he can buy them from her at a price she's willing to accept. Side payments let us interpersonally compare valuations.
As I understand it, economic surplus isn't a subjective quantity. It's a measure of how much people would be willing to pay to go from the status quo to some better outcome. Which might start out as private information in people's heads, but there is an objective answer and we can elicit the information needed to compute and maximize it.
I don't know of any results that suggest this should be true! My understanding of the classic analysis of the Ultimatum game is that if Bob makes a take-it-or-leave-it offer to Alice, where she would receive any tiny amount of money like $0.01, she should take it because $0.01 is better than $0.
My current take is that CDT-style thinking has crippled huge parts of economics and decision theory. The agreement of both parties is needed for this $1,000,000,000 of surplus to exist, if either walk away they both get nothing. The Ultimatum game is symmetric and the gains should be split symmetrically.
If we actually found ourselves in this situation, would we actually accept $1 out of $1 billion? Is that how we’d program a computer to handle this situation on our behalf? Is that the sort of reputation we’d want to be known for?