2 Answers sorted by
41
Let's solve this problem without trying to refer to existing particular cases.
For the start, we assume that utility of A-the-thief monotonically decreases with time served; utility of B monotonically increases, and if A gives up lollipops it is increased by another constant.
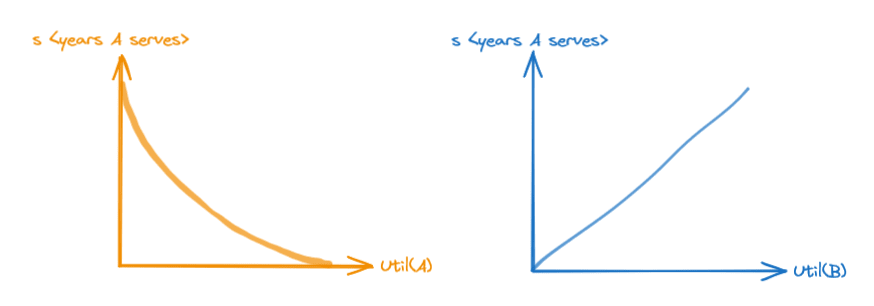
Let's graph what choices A has when B does not give up lollipops.
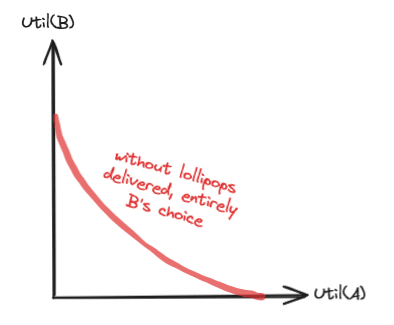
We may notice that in this case B will simply throw A in jail for life. Well, what happens if A is willing to cooperate a bit?
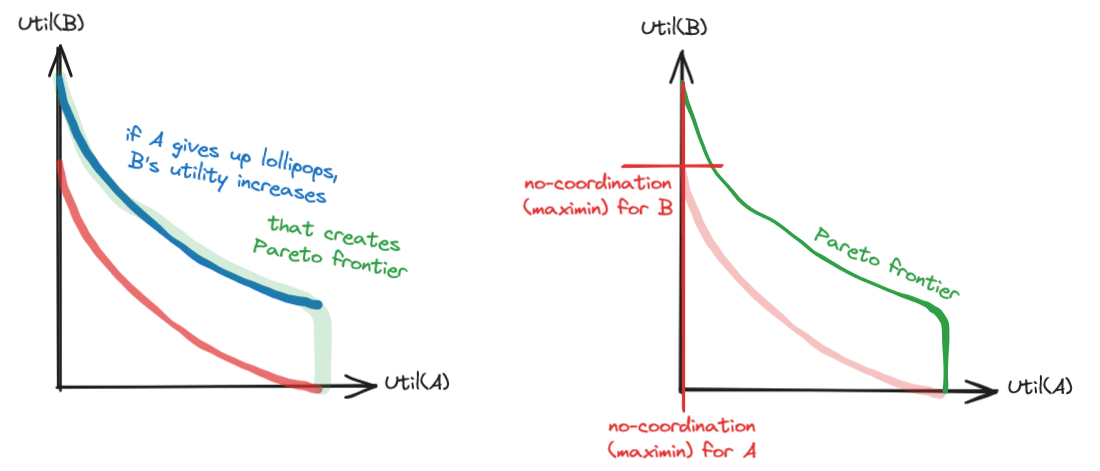
- Coordination result will not be below or to the left of Pareto frontier, since otherwise it is possible to do better than that;
- Coordination result will not be below or to the left of no-coordination result, since otherwise one or both parties are acting irrationally.
We may see that after these conditions, only a piece of curve "A gives up lollipops" remains. The exact bargaining point can then be found out by using ROSE values, but we can already conclude that A will likely be convicted for a long time but not for life.
10
It’s that the description of a monopoly? Like if A has other choices to buy from than B, B can’t exert as much pressure on A.
Isn't this basically just a negotiated trade, from a game theory point of view? The only uncommon feature is that A intrinsically values s at zero and B knows this (and that A is the only supplier of s). This doesn't greatly affect the analysis though, since most of the meat of the problem is what division of gains of trade may be acceptable to both.
It's not actually iterated, it just allows communication before the final agreement (or not). Simply assign values for each player for s and t, and you can calculate various equilibrium outcomes. For fun, it's not guaranteed that either party knows the other's utility function over (s,t), so you can make each player assign a distribution of utilities for the other, and figure out the optimum for each. Then negotiation can reveal some of it (or can fail and lead to sub-optimal outcomes).
Mostly looking for a name, or better even, reference to literature, for this type of problem in terms of game theory or economics. If no such thing, speculation welcome.
Intro below is more or less how I originally came to think of it and felt like writing, please skip unless you have already read the rest of the internet and found your way back here.
[intro]
Its been a dark month, turning upside down every last rock in every last alley in this god-forsaken city. "The things we see in this job", you think to yourself, as your phone starts to ring. But hey! You seem to have caught a break. You rush to the station
And there he is, right as you enter the interrogation cell, staring back across the room with those demented, demented eyes. The kind of look that sits like lead in the bottom of your guts. The kind of look only a man that has stolen 31 lollipops in broad daylight could summon. And right then, you know. You have him, dead to rights. The city can sleep at last.
Or can it?
"Its not as easy as you put it, as per usual" Assistant DA Alice says, as every Assistant DA in every gritty cop story has said before her "We still haven't found the sticks for Lollipops number 6,16 , 25 and 30, and we owe those candy shop owners some closure, if nothing else" she says, as you think of Bob, who lost seven of his lollipops to the first citywide rampage of the very man you have in custody. Almost a decade later and you still think of him, of what has been taken from him. You just noticed your fist has been closed the whole time.
"He says he can deliver the sticks we are missing. Wants only 5 years."
"5 years, down from life?" You shout, barely able to stand still.
"I told him 5 is a non starter. But there is a lot to consider here"
"Politics", you grunt, grinding your teeth in a very manly fashion
"If there is no plea, we still have a very good chance to put him in jail for good, but no lollipop sticks for us. However, in a suspiciously convenient turn of events, the judge has forgotten the maximum time allowed before pressing charges and we still have a month to negotiate."
[end of intro]
Okay, so,
player A has (t, s) as resources. He wants to minimize t. He doesn't mind giving his s away.
player B has (t, s) as resources. He wants to maximize t. He wants to maximize his s.
If they don't agree on an arrangement after a certain number of iterations, t is maximized (originally, you would have a fixed, high chance of conviction, but seems simpler to solve first without this) and s lost. This is an acceptable situation for B but less so for A, as from his perspective any number of s he has to give away for any number of t is worth it, this is saying, any t:s exchange ratio B offers, A should take. (Similarity to the Ultimatum is discussed below)
A few things I think this is not:
As I said, a name would be appreciated, as would any possible strategies you might come up with.