Where do the edges you draw come from? IIUC, this method should result in a collection of features but not say what the edges between them are.
IIUC, the binary masking technique here is the same as the subnetwork probing baseline from the ACDC paper, where it seemed to work about as well as ACDC (which in turn works a bit worse than attribution patching). Do you know why you're finding something different here? Some ideas:
The SP vs. ACDC comparison from the ACDC paper wasn't really apples-to-apples because ACDC pruned edges whereas SP pruned nodes (and kept all edges betwen non-pruned nodes IIUC). If Syed et al. had compared attribution patching on nodes vs. subnetwork probing, they would have found that subnetwork probing was better.
There's something special about SAE features which changes which subnetwork discovery technique works best.
I'd be a bit interested in seeing your experiments repeated for finding subnetworks of neurons (instead of subnetworks of SAE features); does the comparison between attribution patching/integrated gradients and training a binary mask still hold in that case?
I'm not that convinced that attributing patching is better then ACDC - as far as I can tell Syed et al only measure ROC with respect to "ground truth" (manually discovered) circuits and not faithfulness, completeness, etc. Also Interp Bench finds ACDC is better than attribution patching
You are correct that the current method will only give a set of features at each selected layer. The edges are intended to show the attention direction within the architecture. We updated it to make it more clear and fix some small issues.
We think there are a few reasons why the results of the ACDC paper do not transfer to our domain:
ACDC and EAP (Syed et al.) rely on overlap with a manual circuit as their metric, whereas we rely on faithfulness and completeness. Because the metrics are different, the comparison isn’t apples-to-apples.
The major difference between methods, as you mentioned, is that we are finding circuits in the SAE basis. This quite possibly accounts for most of the differences.
The SAEs vs neurons comparison is something we definitely want to test. However, the methods mentioned above (ACDC, eap, etc) used transformer components (MLP, Attn) as their units for circuit analysis. Our setup would need to rely on neurons of the residual stream. We don’t think residual neurons are directly comparable to transformer components because they are at different levels of granularity.
My notes / thoughts: (apologies for overly harsh/critical tone, I'm stepping into the role of annoying reviewer)
Summary
Use residual stream SAEs spaced across layers, discovery node circuits with learned binary masking on templated data.
binary masking outperforms integrated gradients on faithfulness metrics, and achieves comparably (though maybe narrowly worse) completeness metrics.
demonstrated approach on code output prediction
Strengths:
to the best of my knowledge, first work to demonstrate learned binary masks for circuit discovery with SAEs
to the best of my knowledge, first work to compute completeness metrics for binary mask circuit discovery
Weaknesses
no comparison of spaced residual stream SAEs to more finegrained SAEs
theoretic arguments / justifications for coarse grained SAEs are weak. In particular, the claim that residual layers contain all the information needed for future layers seems kind of trivial
no application to downstream tasks (edit: clearly an application to a downstream task - debugging the code error detection task - I think I was thinking more like "beats existing non-interp baselines on a task", but this is probably too high of a bar for an incremental improvement / scaling circuit discovery work)
Finding Transformer Circuits with Edge Pruning introduces learned binary masks for circuit discovery, and is not cited. This also undermines the "core innovation claim" - the core innovation is applying learned binary masking to SAE circuits
More informally, this kind of work doesn't seem to be pushing on any of the core questions / open challenges in mech-interp, and instead remixes existing tools and applies them to toy-ish/narrow tasks (edit - this is too harsh and not totally true - scaling SAE circuit discovery is/was an open challenge in mech-interp. I guess I was going for "these results are marginally useful, but not all that surprising, and unlikely to move anyone already skeptical of mech-interp")
Of the future research / ideas, I'm most excited about the non-templatic data / routing model
On strengths, we also believe that we are the first to examine “few saes” for scalable circuit discovery.
On weaknesses,
While we plan to do a more thorough sweep of SAE placements and comparison, the first weakness remains true for this post.
Our major argument for the support of using few SAEs is imaging them as interpretable bottlenecks. Because they are so minimal and interpretable, they allow us to understand blocks of the transformer between them functionally (in terms of input and output). We were going to include more intuition about this but were worried it might add unnecessary complications. We mention the fact about residual stream to highlight that information cannot be passed to layer L+1 by any other path than the residual output of layer L. Thus, by training a mask at layer L, we find a minimal set of representations needed for future layers. To future layers, nothing other than these latents matter. We do agree that the nature of circuits found with coarse grained saes will differ, and this needs to be further studied.
We plan to explore the “gender bias removal” of Marks et al. [1] to compare the downstream application effectiveness. However, we do have a small application where we found a "bug" in the model, covered in section 5, where it over relies on duplicate token latents. We can try to do something similar to Marks et al.[1] in trying to "fix" this bug
Thanks for sharing the citation!
A core question shared in the community is whether the idea of circuits is plausible as models continue to scale up. Current automated methods either are too computationally expensive or generate a subgraph that is too large to examine. We explore the idea of a few equally spaced SAEs with the goal of solving both those issues. Though as you mentioned, a more thorough comparison between circuits of different numbers of saes is needed.
Thanks for the thorough response, and apologies for missing the case study!
I think I regret / was wrong about my initial vaguely negative reaction - scaling SAE circuit discovery to large models is a notable achievement!
Re residual skip SAEs: I'm basically on board with "only use residual stream SAEs", but skipping layers still feels unprincipled. Like imagine if you only trained an SAE on the final layer of the model. By including all the features, you could perfectly recover the model behavior up to the SAE reconstruction loss, but you would have ~no insight into how the model computed the final layer features. More generally, by skipping layers, you risk missing potentially important intermediate features. ofc to scale stuff you need to make sacrifices somewhere, but stuff in the vicinity of Cross-Coders feels more comprising
Yes -- By design, the circuits discovered in this manner might miss how/when something is computed. But we argue that finding the important representations at bottlenecks and their change over layers can provide important/useful information about the model.
One of our future directions, along the direction of crosscoders, is to have "Layer Output Buffer SAEs" that aim to tackle the computation between bottlenecks.
Very cool work! I think scalable circuit finding is an exciting and promising area that could get us to practically relevant oversight capabilities driven by mechint with not too too long a timeline!
Did you think at all about ways to better capture interaction effects? I've thought about approaches similar to what you share here and really all that's happening is a big lasso regression with the coefficients embedded in a functional form to make them "continuousified" indicator variables that contribute to the prediction part of the objective only by turning on or off the node they're attached to. As is of course well known, lasso tends to select representative elements out of groups with strong interactions, or miss them entirely if the main effects are weak while only the interactions are meaningful. The stock answer in the classic regression context is to also include an L2 penalty to soften the edges of the L1 penalty contour, but this seems not a great answer in this context. We need the really strong sparsity bias of the solo L1 penalty in this context!
I don't mean this as a knock on this work! Really strong effort that would've just been bogged down by trying to tackle the covariance/interaction problem on the first pass. I'm just wondering if you've had discussions or thoughts on that problem for future work in the journey of this research?
I'm a little confused what it means to mean-ablate each node...
Oh, wait. ctrl-f shows me the Non-Templatic data appendix. I see, so you're tracking the average of each feature, at each point in the template. So you can learn a different mask at each token in the template and also learn a different mean (and hopefully your data distribution is balanced / high-entropy). I'm curious - what happens to your performance with zero-ablation (or global mean ablation, maybe)?
Excited to see what you come up with for non-templatic tasks. Presumably on datasets of similar questions, similar attention-control patterns will be used, and maybe it would just work to (somehow) find which tokens are getting similar attention, and assign them the same mask.
It would also be interesting to see how this handles more MLP-heavy tasks like knowledge questions. maybe someone clever can find a template for questions about the elements, or the bibliographies of various authors, etc.
Thanks! We use mean ablation because this lets us create circuits including only the things which change between examples in a task. So, for example, in the code task, our circuits do not need “is python” latents, as these latents are consistent across all samples. Were we to zero ablate, we would need every single SAE latent necessary for every part of the task. This includes things which were consistent across all tasks! This means many latents which we don’t really care about are included in our circuits.
I've been leveraging your code to speed up implementation of my own new formulation of neuron masks. I noticed a bug:
def running_mean_tensor(old_mean, new_value, n):
return old_mean + (new_value - old_mean) / n
def get_sae_means(mean_tokens, total_batches, batch_size, per_token_mask=False):
for sae in saes:
sae.mean_ablation = torch.zeros(sae.cfg.d_sae).float().to(device)
with tqdm(total=total_batches*batch_size, desc="Mean Accum Progress") as pbar:
for i in range(total_batches):
for j in range(batch_size):
with torch.no_grad():
_ = model.run_with_hooks(
mean_tokens[i, j],
return_type="logits",
fwd_hooks=build_hooks_list(mean_tokens[i, j], cache_sae_activations=True)
)
for sae in saes:
sae.mean_ablation = running_mean_tensor(sae.mean_ablation, sae.feature_acts, i+1)
cleanup_cuda()
pbar.update(1)
if i >= total_batches:
break
get_sae_means(corr_tokens, 40, 16)
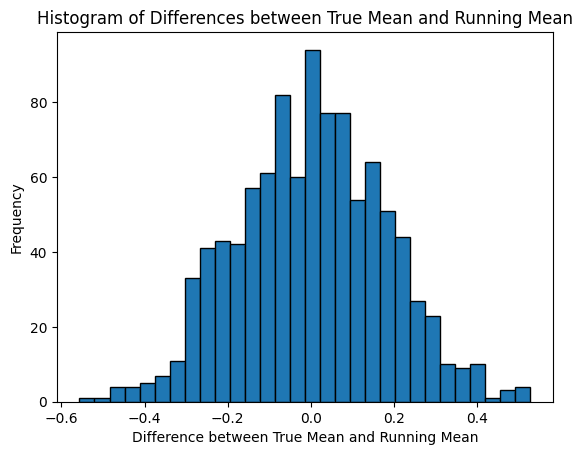
The running mean calculation is only correct if n is the total number of samples so far. But i+1 is the 1-indexed batch number we're on. That value should be i * batch_size + j + 1. I ran a little test. Below is a histogram from 1k runs of taking 104 random normal samples with batch_size=8, and then comparing the different between the true mean and the final running mean as calculated by the running_mean_tensor function. It looks like the expected difference is zero but with a fairly large variance. Def larger than standard error of the mean estimate, which is ~1/10 (= standard_normal_sdev / sqrt(n) =~ 1/10). Not sure how much it affects accuracy of estimates to add a random error to the logit diffs.
Scaling SAE Circuits to Large Models: By placing sparse autoencoders only in the residual stream at intervals, we find circuits in models as large as Gemma 9B without requiring SAEs to be trained for every transformer layer.
Finding Circuits: We develop a better circuit finding algorithm. Our method optimizes a binary mask over SAE latents, which proves significantly more effective than existing thresholding-based methods like Attribution Patching or Integrated Gradients.
Our discovered circuits paint a clear picture of how Gemma does a given task, with one circuit achieving 95% faithfulness with <20 total latents. This minimality lets us quickly understand the algorithm for how a model does a given task. Our understanding of the model lets us find vulnerabilities in it and create successful adversarial prompts.
1 Introduction
Circuit finding, which involves identifying minimal subsets of a model capable of performing specific tasks, is among the most promising methods for understanding large language models. However, current methods face significant challenges when scaling to full-size LLMs.
Early circuit finding work focused on finding circuits in components like attention heads and MLPs. But these components are polysemantic - each one simultaneously performs multiple different tasks, making it difficult to isolate and understand specific model behaviors. Sparse autoencoders (SAEs) offered a solution by projecting model activations into an interpretable basis of monosemantic latents, each capturing a single concept.
While SAEs enable more granular circuit analysis, current approaches require placing autoencoders at every layer and component type (MLP, attention, residual stream). This becomes impractical for large models - for llama-70B with 80 layers, you would need 240 separate SAEs. Additionally, the resulting circuits often contain thousands of nodes, making it difficult to extract a clear algorithmic understanding.
We propose a simpler and more scalable approach. The residual stream at a given layer contains all information used by the future layers. By placing residual SAEs at intervals throughout the model rather than at every layer, we can find the minimal set of representations that are needed to maintain task performance. This not only reduces computational overhead but actually produces cleaner, more interpretable circuits.
Our second key innovation is the use of a binary mask optimized through continuous sparsification [10] to identify circuits. Continuous sparsification gradually reduces the importance of less relevant elements during optimization, allowing for a more synergistic selection of circuit components. This method replaces traditional thresholding-based approaches like Integrated Gradients used by Marks et al. [1]. By optimizing a binary mask over SAE latents, we can find minimal sets of latents that maintain task performance. This approach significantly outperforms previous methods, finding smaller circuits that better explain model behavior in terms of logit diff recovery.
The combination of these techniques - strategic SAE placement and learned binary masks via continuous sparsification - allows us to scale circuit finding to Gemma 9B while producing human-interpretable results. We demonstrate this on several tasks, including subject-verb agreement and dictionary key error detection, and reveal clear algorithmic patterns in how the model processes information. Using our knowledge of the algorithms implemented, we are able to find bugs in them and design adversarial examples that cause the full model to fail in predictable ways.
2 Background
2.1 SAEs
Sparse Autoencoders (SAEs) are used to project model activations into a sparse and interpretable basis, addressing the challenge of polysemantic neurons [3]. By focusing on sparse latents, SAEs provide a more interpretable unit of analysis for understanding model behavior because each latent corresponds to a single, human-interpretable concept.
However, while SAEs improve interpretability, the resulting representations still include a significant amount of a-causal noise. Many active latents do not impact performance when ablated. This noise complicates attempts to produce concise and human-understandable summaries of the model's computations during a forward pass.
2.2 Circuits
Circuit discovery involves identifying subsets of a model’s components responsible for specific behaviors (eg indirect object recognition). The importance of a component in the model computational graph is calculated via its indirect effect (IE) on some task-relavent loss function [8]. However, computing IE for all components is expensive, so it is typically approximated by attribution patching [11]. The work by Syed et al. [7] provided a way to linearly approximate change in loss L by replacing activation a with ablation a′ within model m:
IEatp=(a′−a)⋅∇aL(m(a))
However, if the loss function L has a gradient of 0 at a, the equation becomes:
IEatp=(a′−a)⋅0
causing an underestimation of the true causal impact of replacing a with a′ on L. Thus, integrated gradients [12, 4] was introduced. IG accumulates the gradients along the straight-line path from a to a', improving causal impact approximations.
Sparse Feature Circuits (SFC), introduced by Marks et al. [1], was one of the first approaches to circuit discovery in the SAE basis, allowing for fine-grained interpretability work. Their approach uses SAEs placed at every MLP, attention, and residual layer. It relies on Integrated Gradients to attribute performance to model components. After integration, a circuit is selected by filtering for any latents whose approximated IE is above a selected threshold value.
2.3 Problems with Current Sparse Feature Interpretability Approaches
2.3.1 Scalability
Although Marks et al. [1] successfully scaled circuit discovery to Gemma 2 2b [13], the method encounters significant scalability issues. This is because it requires three SAEs at every transformer layer, which becomes increasingly impractical as model sizes grow. Usually, more SAE parameters are needed than actual model parameters! As the model scale increases beyond trillions of parameters [9], this work does not realistically scale.
2.3.2 Independent Scoring of Nodes
Most automated methods for circuit discovery [1, 6, 7] begin by first calculating (or approximating) the IE for each component. After IE approximation, a circuit is selected by filtering for any latents whose approximated IE is above a selected threshold value. This overlooks collective behaviors and self consistency of selected circuit components. ACDC [6] attempts to solve this problem by iteratively pruning, which increases accuracy [4]. However, it is too computationally expensive.
2.3.3 Error Nodes
Although SAEs are optimized to minimize reconstruction error, they are not perfect. Each SAE introduces a small amount of noise. When a model is instrumented with many SAEs, the errors introduced by each one accumulate and all but destroy model performance. To resolve this, Marks et al. [1] include error nodes: an uninterpretable vector containing SAE reconstruction error added to SAE output. With this addition, each SAE is now an identity function. This solves the compounding error problem, but at the cost of interpretability. Without error nodes, there was a guarantee that any information represented by a SAE was contained in its sparse coding. With error nodes, they leak uncoded information.
This introduces an incentive problem. In a SAE circuit finding scenario without error nodes, better SAEs produce more faithful circuits for a given number of circuit components. However, with error nodes, a worse SAE will reconstruct less of its input, causing uncoded information to move into the single error node. Thus, as the SAEs get worse, the number of circuit components required to achieve a given level of faithfulness actually decreases because more information is contained in the error node. By the metrics of faithfulness per number of components, worse SAEs produce better circuits. Ideally, circuit finding metrics would improve monotonically as SAEs become better, but error nodes get rid of this monotonicity.
3 Our Approach
Here we detail our approach to tackling the problems current circuit discovery methods face. We introduce two main innovations:
Circuits with few residual SAEs, allowing us to scale to larger models
A better circuit finding algorithm that produces more faithful circuits for a given number of components
We detail the motivations below.
3.1 Solving Scalability: Circuits with few residual SAEs
As previously mentioned, we place only a few residual SAEs throughout the forward pass for scalability purposes. Why is this a reasonable choice?
Because residual SAEs contain all of the information of the forward pass at Layer L, we know that all future layers will rely purely on this information. This is unlike Attention and MLP SAEs, that are in parallel to the residual stream, meaning that future layers will rely on not only their output but also the residual stream. Thus, at every SAE layer, nodes in circuits that we find contain all of the information that the future layers will rely on. It is important to note that by design, our circuits don't cover how or when something is computed, only what is necessary.
3.2 Solving Independent Scoring: Masking
To select subsets of networks, apply continuous sparsification [10] to optimize a binary mask over nodes while maintaining faithfulness. We find this outperforms thresholding based approaches (IG, ATP) in terms of faithfulness, and hypothesize the reason is that our approach considers how latents work together, in addition to their causal impact. A toy example demonstrates a failure mode of threshold-based approaches below:
Continuous sparsification (learning a binary mask) over circuit components produces more faithful circuits than activation patching and integrated gradients in this toy scenario.
3.3 Error nodes
Because we have fewer SAEs and better circuit finding algorithms, we are able to recover significant performance without any error nodes. Thus, in our experiments, we do not include any error nodes.
4 Results
4.1 Setup
In our setup of 4 residual SAEs every ~10 layers, we find circuits on nodes (SAE latents), and because our data is templatic, we learn per-token circuits, similar to Marks et al. [1]. When ablating a node, we replace it with a per-token mean ablation. Finally, the metric used for measuring performance and calculating attribution is the logit difference between the correct and incorrect answer for a task. For learned binary masks, we optimize the logit diff of our circuit to match the logit diff of the model.
We compare our circuit finding algorithm, learned binary masking with integrated gradients, the algorithm used by Marks et al. [1].
We find circuits for two python code output prediction tasks, for the Indirect Object Identification (IOI) task, and for the task of subject verb agreement (SVA) over a relative clause.
Within our learned circuits, we analyze the following criteria:
Faithfulness Frontier
Completeness
Stability
Causal Story
Sections 4.2 - 4.4 provide information on performance recovery, and checks for stability and completeness of circuits discovered.
4.2 Performance Recovery
The first requirement for a circuit is to recover a significant portion of the performance of the full model for the task it was discovered on. This is computed as Faithfulness [5] - the ratio of circuit performance to model performance.
We have evaluated our methods on 3 different tasks, each with a separate goal.
The code output prediction tasks are selected because they are only possible in large models (>2B).
The SVA (subject verb agreement) task was chosen because it the primary task explored by Marks et al. [1].
The IOI circuit is an attention based mechanism, while our approach focuses only on residual streams. This allows us to test our methods in a regime where we do not expect good performance.
We go into more detail about the tasks and their significance in section 5.
In all three of our tasks, learned binary masking was able to recover more performance with less latents than integrated gradients. However, the performance/sparsity frontiers of IG and learned binary masking differed between tasks.
4.2.1 Code Output Prediction:
This task assesses the model capabilities to predict Python code outputs. In addition to predicting correct code outputs, each of our tasks also includes buggy code, which makes them even harder. Smaller models are unable to complete this logic-based task.
4.2.1.1 Dictionary Key
This task involves keying into a dictionary. There are two cases, one where the key exists in the dictionary and another where it doesn't, causing a Traceback.
>>> age = {"Bob":12, "Alice":15, "Rob":13, "Jackson":11, "Tom": 19}
>>> age["Maria"]
Expected next token: Traceback
=============================
>>> age = {"Bob":12, "Alice":15, "Rob":13, "Jackson":11, "Tom": 19}
>>> age["Bob"]
Expected next token: 1
Learned masking significantly outperforms integrated gradients in this example.
IG fails to recover even >50% performance.
The task requires more latents to recover significant performance than other tasks
Faithfulness of 1 means our circuit recovers 100% of performance on task, while 0% means we recover 0% of the task. The green line represents the faithfulness of the full model with SAEs. We do not exceed this because our circuits inherit the limitations of the SAEs, and we do not use error nodes.
4.2.1.2 List Index
This example deals with indexing into a list, with a similar setup to the previous task.
Similar to the dictionary keying task shown above, learned masking is able to select circuits which are more faithful for any given number of nodes.
4.2.2 Subject Verb Agreement (SVA):
In this task, the goal is to choose the appropriate verb inflection (singular, plural) based on the plurality of the subject. We use the variant of SVA across a relative clause for the results below.
Example:
The carpenters that the dancers praise
Expected next token: are
=======================
The carpenter that the dancers praise
Expected next token: is
Analysis:
SVA is a relatively easy task that is even possible for pythia-70m, as shown by Marks et al. [1].
Here, IG and learned binary masking have more similar performance.
Still, learned binary masking finds circuits with fewer latents that are more faithful.
4.2.3 IOI:
In this task, the goal is to identify the indirect object in the sentence, proposed by Wang et al. [5].
Example:
Clean Prompt = "When Mary and John went to the store, John gave a drink to"
Expected next token = "Mary"
Corrupted Prompt = "When David and Bob went to the store, Emily gave a drink to"
Analysis:
The discovered mechanism by Wang et al. [5] is attention based, relying on duplicate token heads, name movers, induction heads, and more. We chose this as a stress test for our methods.
Because we have residual SAEs, every SAE needs to contain all of the information future layers require. For any given name to pass through the entire model, it needs a node in every SAE.
Thus, number of nodes required to recover performance is quite high. We find many latents related to individual names when inspecting the circuit.
Again, learned masking finds circuits with greater faithfulness and fewer latents than IG.
4.3 Completeness
As our binary mask training method does not involve explicit indirect effect calculation, it might be possible that we find circuits containing a set of latents that optimize the performance of the task but aren’t actually used by the model. To make sure that this is not occurring we rely on the completeness metric - a measure of how much the entire model's performance is harmed by removing nodes from within our circuit.
Different papers have proposed a few methods to measure this. Wang et al. [5] measure completeness by comparing how a circuit its parent model behave under random ablations of components from the circuit. If removing a subset of the circuit from both the circuit and model causes a similar drop in performance, this provides some evidence that the same latents important for a given task are also important for the whole model.
In the figure below, we create 5 random subsets (each 14 nodes) in the circuit we discovered for the subject verb agreement task with 55 nodes. We mean-ablate these latents from both the model and circuit, and calculate logit diff between the correct and incorrect answer tokens.
The y axis shows the logit diff (higher=better) of the model under K knockout and the x axis shows the logit diff (higher = better) of the circuit under K knockout. Most points are close to the y=x line, signifying that model and circuit are behaving similarly under ablations. Red: ablate nothing, green: ablate full circuit
For a given task, if only the nodes within the circuit are used by the full model, we would expect all points to lie on the y=x line. However, if the latents within the circuit are not used by the full model, or if the circuit only captures a portion of the nodes important for the full model, we would expect the slope to decrease.
Within the above figure, many of the points are close to the y=x line, suggesting that model and circuit do behave similarly under ablation and that we are not missing large important latents mediating model behavior in our circuit.
Furthermore, we also plot the performance of the model and circuit when ablating the entire circuit shown in the green data point. Here removing the entire circuit causes the performance to drop to 0 (random chance between the two expected outputs).
Marks et al. [1] measure completeness in a different way. Because they are able to automatically generate circuits for any number of desired nodes, they instead measure completeness as the performance of the full model when an entire circuit is mean-ablated. They generate a frontier of number of nodes in circuit vs. logit-diff of model w/o circuit, showing how the full model's performance decreases as the circuit contains more nodes, and thus more nodes in the full model are ablated.
For SVA:
For Error Prediction - Key Error:
For both the above graphs, we find that IG and masking can get completeness near 0, In some cases, IG scores slightly closer to 0.
4.4 Mask Stability
To assess the stability of our circuit discovery method, we examined whether different hyperparameter settings consistently identify the same underlying circuit components. We trained 10 different binary masks by varying the sparsity multiplier, which controls circuit size (lower multipliers yield larger circuits). Our analysis revealed that circuits exhibit strong nested structure: latents present in smaller circuits (those trained with higher sparsity multipliers) are nearly always present in larger circuits (those trained with lower sparsity multipliers). This consistency across hyperparameter settings suggests our method reliably identifies core circuit components.
5 Case Study: Code Output Prediction
This section showcases how our approach to circuit discovery addresses real-world challenges in model interpretability. By leveraging masking, which significantly outperforms Integrated Gradients (IG), we achieve scalable, interpretable, and minimal circuits. These circuits allow for faster mechanistic understanding and provide insights into model vulnerabilities. Below, we showcase an example of this with the dictionary key error detection. We aim to focus on understanding the mechanism of other circuits in the following work.
Mechanism: Our approach uncovers how the model relies on duplicate token latents to determine if the key exists and outputs the corresponding value. If no duplicates are detected, it switches to generating error tokens like Traceback.
Insights:
The circuit shows the model is heavily reliant on "detect duplicate" latents to decide if a key exists. However, these latents trigger on all duplicate tokens, not only ones which are keys in the dictionary.
Vulnerability: The model is over-reliant on the duplicate token latents. This knowledge of the model's algorithm lets us create an adversarial dictionary, where the query is present as a value, rather than a key.
Original Prompt:
>>> age = {"Isabella": 19, "Emma": 18, "Tom": 17, "Ethan": 18, "Ava": 12}
>>> age["Ethan"]
================
Top 0th token. Logit: 28.38 Prob: 95.00% Token: |1| (Correct Token)
Top 1th token. Logit: 24.77 Prob: 2.56% Token: |>>>|
Top 2th token. Logit: 22.56 Prob: 0.28% Token: | |
As we expect from our understanding of the circuit, the adversarial prompt causes the model to produce the wrong answer because the token Ethan is replicated, the model fails to recognize the error.
Significance:
Smaller models struggle with this task, highlighting its non-trivial nature.
Understanding the causal mechanism for error detection and code output prediction lets us find a "bug" in Gemma 9B.
6. Conclusions
This work introduces a scalable and interpretable approach to circuit discovery in large language models. By placing residual SAEs at intervals and using binary mask optimization, we significantly reduce computational overhead of training multiple SAEs at every layer while uncovering more minimal and human-interpretable circuits and avoiding error nodes.
In specific, we are excited about the following aspects of our work:
Learned binary masking via continuous sparsification pareto dominates other circuit-finding algorithms for faithfulness in our experiments. We hope to apply this approach to other circuit-finding tasks.
We were able to analyze circuits in the regime of truly large language models. Our approach is unique in that it has promise to scale to models in the hundreds of billions of parameters. Most critically, we don't need SAEs trained at every single layer, which is extremely costly.
The algorithms we find in these models are concise enough for us to understand them and find bugs.
Despite the promise of our work, there are still some limitations of our methodology. Most significantly, by design, our approach doesn't find how or when something was computed; it only looks at what representations matter. Because we use residual SAEs, each SAE contains a summary of all the dependencies of the future layers. However, this does not tell us where something is computed. If an important latent variable is computed early in the network and is only needed at the end, we still see it in every SAE.
When analyzing the IOI circuit, this limitation of our methodology becomes apparent. At the first layer, as expected, we find many latents corresponding to individual names. However, for any given name to propagate through the entire model and be used as a prediction, it needs a latent at every single SAE. Even if none of the middle layers actually modify the latent, circuits which successfully perform IOI on this name require the middle SAEs to have latents which let the name pass through. The amount of different latents necessary in every single SAE makes circuit analysis difficult.
Additionally, some other open questions remain:
What is the best way to pick the number and location of SAEs? - we are not sure yet; we plan to do a sweep comparing circuits discovered with different places and numbers of SAEs
How well does learned binary masking perform in other regimes?
7. Future Research and Ideas
More interesting tasks on larger models:
Our success in finding extremely simple yet faithful circuits suggests that our method can scale to more complex algorithmic tasks. We plan to extend this work to attempt to understand how language models perform tool use, general code interpretation, and mathematical reasoning.
A potential next step would be to analyze a broader range of code runtime prediction tasks, building on benchmarks from Chen et al. [15] and Gu et al. [14].
We hope to identify computational commonalities across different coding tasks and discover model vulnerabilities, as we did with dictionary key detection.
Exploit the Residual Stream: Layer Output Buffer SAEs
As earlier stated, residual SAEs come with some limitations, namely:
We don't directly see where something was computed, only that it exists and matters
For some information to propagate to the end of the model, it must be unmasked (not to mention represented) in every SAE. Rather than capturing a diff the residual stream, each SAE contains the whole residual state.
This makes our circuits less minimal and interpretable
While using MLP/Attn SAEs lets us capture only diffs, therefore resolving these problems, this is not scalable. It requires a SAE at every model layer. How can we capture the benefits of both residual SAEs (we only need a few to capture an entire computation) and MLP/Attn SAEs (captures residual stream diffs, making more minimal circuits)?
A proposal: Layer Output Buffer SAEs
Only place an SAE after every ≈ 10 transformer layers
We have residual stream state a at transformer layer 10 and residual stream state b at transformer layer 20. Rather than learning an SAE on b, we learn a SAE on b-a. In other words, we learn the diff applied on the residual stream from layers 10 through 20.
Learn an SAE on this diff
A residual SAE captures the output of the entire computation occurring up to a certain point in the model. This approach would train SAEs on the outputs of only the past few transformer layers
This approach for training SAEs could be the best of both worlds (attn/mlp SAEs, resid SAEs). It lets us capture the full computation of the LLM with only a few SAEs, while still only intervening on diffs to the residual stream.
Apply to Edges
In this work, we applied our approach to nodes only. In the future, we want to find the important edges within our circuits as well. Jacobian approximation of edge effects could be used, perhaps also in combination with learned binary masks on edges.
Non-Templatic Data
We only apply our approaches to templated data, where token positions each have separate roles, letting us learn a different subset of the model for each token. This makes circuits much easier to understand. Additionally, it gives us per-token means.
However, when a task is non-templatic, we no longer have the ability to create per-token means or circuits. We must do zero-ablation and learn a single circuit which encompasses all token roles. This is especially unfortunate because many more complicated tasks which we might be interested in are non-templatic.
A potential solution:
By routing based on token index, where each token index is a role, we are implicitly creating a router which maps each token role to a different model subset.
If we frame this as a mapping problem, we can imagine learning a classifier which routes tokens in a sequence to roles, where each role gets a specific model subset.
We could learn the role-router and the model subsets at the same time.
This could let us discover roles and corresponding model subsets in an unsupervised manner, letting us still have the power to use different circuits for different token roles while analyzing non-templatic tasks.
Iterated Integrated Gradients
We believe the reason binary mask optimization works better than integrated gradients is because it finds a more coherent circuit by selecting latents in an interdependent manner. Could we iterate integrated gradients, each time only removing the least causally impactful set of latents to produce more coherent circuits?
Understand why learned binary masks outperform IG
We hypothesize that learned binary masking outperforms thresholding based circuit approaches (IG, activation patching, ATP) because it selects a set of self-consistent latents. We are able to demonstrate this in a toy model. However, we want to do a deeper investigation of this. An easy way to test our hypothesis is to look at the causal impact of latents within their selected circuits. Given our hypothesis that IG selects latents which end up "orphaned" or with no way to propagate, we would expect another pass of IG on a thresholded circuit to find latents with some causal attribution in the model, but no attribution in the circuit.
References
[1] Marks, Samuel, et al. "Sparse feature circuits: Discovering and editing interpretable causal graphs in language models." arXiv preprint arXiv:2403.19647 (2024).
[2] Balagansky, Nikita, Ian Maksimov, and Daniil Gavrilov. "Mechanistic Permutability: Match Features Across Layers." arXiv preprint arXiv:2410.07656 (2024).
[3] Templeton, Adly. Scaling monosemanticity: Extracting interpretable features from claude 3 sonnet. Anthropic, 2024.
[4] Hanna, Michael, Sandro Pezzelle, and Yonatan Belinkov. "Have faith in faithfulness: Going beyond circuit overlap when finding model mechanisms." arXiv preprint arXiv:2403.17806 (2024).
[5] Wang, Kevin, et al. "Interpretability in the wild: a circuit for indirect object identification in gpt-2 small." arXiv preprint arXiv:2211.00593 (2022).
[6] Conmy, Arthur, et al. "Towards automated circuit discovery for mechanistic interpretability." Advances in Neural Information Processing Systems 36 (2023): 16318-16352.
[7] Syed, Aaquib, Can Rager, and Arthur Conmy. "Attribution patching outperforms automated circuit discovery." arXiv preprint arXiv:2310.10348 (2023).
[8] Pearl, Judea. "Direct and indirect effects." Probabilistic and causal inference: the works of Judea Pearl. 2022. 373-392.
[10] Savarese, Pedro, Hugo Silva, and Michael Maire. "Winning the lottery with continuous sparsification." Advances in neural information processing systems 33 (2020): 11380-11390.
[12] Mukund Sundararajan, Ankur Taly, and Qiqi Yan. Axiomatic attribution for deep networks. In Proceedings of the 34th International Conference on Machine Learning - Volume 70, ICML’17, pp. 3319–3328. JMLR.org, 2017.
[13] Team, Gemma, et al. "Gemma 2: Improving open language models at a practical size." arXiv preprint arXiv:2408.00118 (2024).
[14] Gu, Alex, et al. "Cruxeval: A benchmark for code reasoning, understanding and execution." arXiv preprint arXiv:2401.03065 (2024).
[15] Chen, Junkai, et al. "Reasoning runtime behavior of a program with llm: How far are we?." arXiv preprint cs.SE/2403.16437 (2024).
[16] Sun, Qi, et al. "Transformer layers as painters." arXiv preprint arXiv:2407.09298 (2024).
1
