TL;DR: does stapling an adaptation executor to a consequentialist utility maximizer result in higher utility outcomes in the general case, or is AlphaGo just weird?

So I was reading the AlphaGo paper recently, as one does. I noticed that architecturally, AlphaGo has

1. A value network: "Given a board state, how likely is it to result in a win". I interpret this as an expected utility estimator.
2. Rollouts: "Try out a bunch of different high-probability lines". I interpret this as a "consequences of possible actions" estimator, which can be used to both refine the expected utility estimate and also to select the highest-value action.
3. A policy network: "Given a board state, what moves are normal to see from that position". I interpret this one as an "adaptation executor" style of thing -- it does not particularly try to do anything besides pattern-match.

I've been thinking of AlphaGo as demonstrating the power of consequentialist reasoning, so it was a little startling to open the paper and see that actually stapling an adaptation executor to your utility maximizer provides more utility than trying to use pure consequentialist reasoning (in the sense of "argmax over the predicted results of your actions").

I notice that I am extremely confused.

I would be inclined to think "well maybe the policy network isn't doing anything important, and it's just correcting for some minor utility estimation issue", but the authors of the paper anticipate that response, and include this extremely helpful diagram:

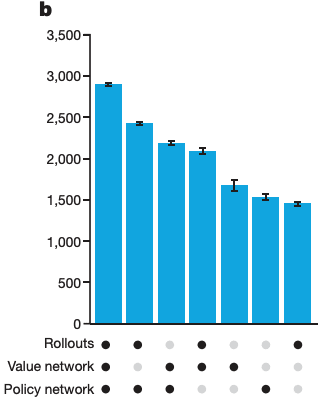
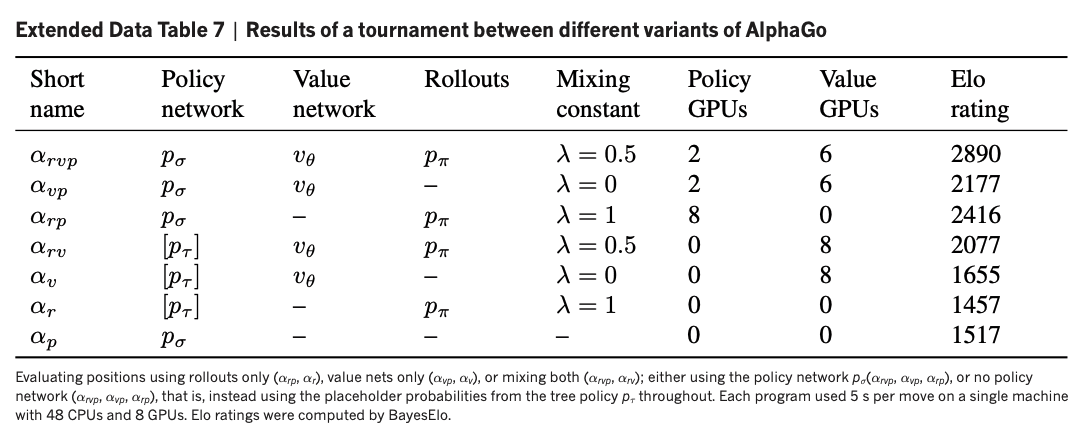
The vertical axis is estimated Elo, and the dots along the X axis label represent which of the three components were active for those trials.

For reference, the following components are relevant to the above graph:

1. The fast rollout policy $p_{\pi }$: a small and efficient but not extremely accurate network that predicts the probability that each legal move will be the next move, based on examining a fixed set of properties of the last move (e.g. "is this move connected to the previous move", "does the immediate neighborhood of this move/the previous move match a predetermined pattern"). Accuracy of 24.2%.
2. The tree rollout policy $p_{\tau }$: like the fast rollout policy, but adds three more features "move allows stones to be captured", "manhattan distance to last 2 moves", and a slightly larger pattern (12 point diamond instead of 3x3 pattern) around this move. Details of both $p_{\pi }$ and $p_{\tau }$ are given in extended data table 4 if you're curious.
3. The SL policy network $p_{\sigma }$: a giant (by the standards of the time) 13 layer NN, pretrained on human games and then further trained through, if I'm reading the paper correctly, learning to imitate a separate RL policy network that is not used anywhere in the final AlphaGo system (because the SL policy network outperforms it)
4. The value network $v_{\theta }$: Same structure as the SL policy network except it outputs what probability the current board state has of being a win for the current player.
5. Rollouts: Pretty standard MCTS

So my question:

Why does the system with the SL policy network do so much better than the system without it?

A couple hypotheses:

1. Boring Answer: The SL policy network just helps to narrow the search tree. You could get better performance by running the value network on every legal move, and then transforming the win probability for each legal move into a search weight, but that would require running the value network ~19x19=361 times per move, which is a lot more expensive than running the SL policy network once.
2. Policy network just adds robustness: A second, separately trained value network would be just as useful as the policy network.
3. Bugs in the value network: the value network will ever-so-slightly overestimate the value of some positions, and ever-so-slightly underestimate the value of others, based on whether particular patterns of stones that indicate a win or loss are present. If there is a board state that is in fact losing, but the value network is not entirely sure that the position is losing, moves that continue to disguise the fact that it is losing will be rated higher than moves that in fact improve the win chance,  but make the weakness of the position more obvious.
4. Consequentialism doesn't work actually: There is some deeper reason that using the value network plus tree search not only doesn't work, but can't ever work in an adversarial setting.
5. I'm misunderstanding the paper: AlphaGo doesn't actually use the SL policy network the way I think it does
6. Something else entirely: These possibilities definitely don't cover the full hypothesis space.

My pet hypothesis is (3), but realistically I expect it's (5) or (6). If anyone can help me understand what's going on here, I'd appreciate that a lot.