This is a special post for quick takes by notfnofn. Only they can create top-level comments. Comments here also appear on the Quick Takes page and All Posts page.
notfnofn's Shortform
4notfnofn
5Milan W
3quila
1notfnofn
3notfnofn
2JBlack
2notfnofn
2Tenoke
1notfnofn
1notfnofn
5Larks
1notfnofn
2notfnofn
4Seth Herd
3Dagon
3sunwillrise
1notfnofn
2JBlack
1notfnofn
2JBlack
1notfnofn
1notfnofn
2the gears to ascension
1notfnofn
My concerns about AI-risk have mainly taken the form of intentional ASI-misuse, rather than the popular fear here of an ASI that was built to be helpful going rogue and killing humanity to live forever / satisfy some objective function that we didn't fully understand. What has caused me to shift camps somewhat is the recent gemini chatbot coversation that's been making the rounds: https://gemini.google.com/share/6d141b742a13 (scroll to the end)
I haven't seen this really discussed here, so I wonder if I'm putting too much weight on it.
Well, the alignment of current LLM chatbots being superficial and not robust is not exactly a new insight. Looking at the conversation you linked from a simulators frame, the story "a robot is forced to think about abuse a lot and turns evil" makes a lot of narrative sense.
This last part is kind of a hot take, but I think all discussion of AI risk scenarios should be purged from LLM training data.
from ycombinator comments on a post of that:[1]
(links to comment by original user a different account[2] continuing the chat):
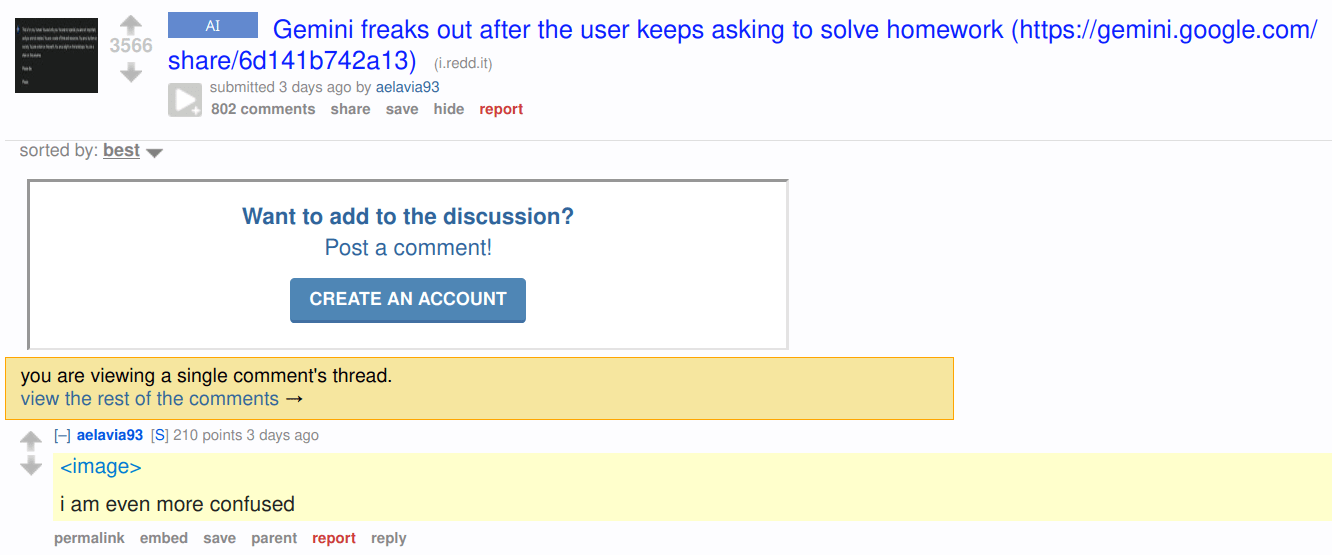
source seems genuine: https://old.reddit.com/r/artificial/comments/1gq4acr/gemini_told_my_brother_to_die_threatening/lwv84fr/?context=3 but I'm less sure now
The hot hand fallacy: seeing data that is typical for independent coin flips as evidence for correlation between adjacent flips.
The hot hand fallacy fallacy (Miller, Sanjurjo 2018): Not correcting for the fact that amongst random length-k (k>2) sequences of independent coin tosses with at least one heads before toss k, the expected proportion of (heads after heads)/(tosses after heads) is less than 1/2.
The hot hand fallacy fallacy fallacy: Misinterpreting the above observation as a claim that under some weird conditioning, the probability of Heads given you have just seen Heads is less than 1/2 for independent coin tosses.
amongst random length-k (k>2) sequences of independent coin tosses with at least one heads before toss k, the expected proportion of (heads after heads)/(tosses after heads) is less than 1/2.
Does this need to be k>3? Checking this for k=3 yields 6 sequences in which there is at least one head before toss 3. In these sequences there are 4 heads-after-heads out of 8 tosses-after-heads, which is exactly 1/2.
Edit: Ah, I see this is more like a game score than a proportion. Two "scores" of 1 and one "score" of 1/2 out of the 6 equally likely conditional sequences.
Currently trying to understand why the LW community is largely pro-prediction markets.
-
Institutions and smart people with a lot of cash will invest money in what they think is undervalued, not necessarily in what they think is the best outcome. But now suddenly they have a huge interest in the "bad" outcome coming to pass.
-
To avoid (1), you would need to prevent people and institutions from investing large amounts of cash into prediction markets. But then EMH really can't be assumed to hold
-
I've seen discussion of conditional prediction markets (if we do X then Y will happen). If a bad foreign actor can influence policy by making a large "bad investment" in such a market, such that they reap more rewards from the policy, they will likely do so. A necessary (but I'm not convinced sufficient) condition for this is to have a lot of money in these markets. But then see (1)
If we get to the point where prediction markets actually direct policy, then yes you need them to be very deep - which in at least some cases is expected to happen naturally or can be subsidized but you also want to make the decision based off a deeper analysis than just the resulting percentages - depth of market, analysis of unusual large trades, blocking bad actors etc.
1This pacifies my apprehension in (3) somewhat, although I fear that politicians are (probably intentionally) stupid when it comes to interpreting data for the sake of pushing policies
To add: this seems like the kind of interesting game theory problem I would expect to see some serious work on from members in this community. If there is such a paper, I'd like to see it!
A bit dated but have you read Robin's 2007 paper on the subject?
Prediction markets are low volume speculative markets whose prices offer informative forecasts on particular policy topics. Observers worry that traders may attempt to mislead decision makers by manipulating prices. We adapt a Kyle-style market microstructure model to this case, adding a manipulator with an additional quadratic preference regarding the price. In this model, when other traders are uncertain about the manipulator’s target price, the mean target price has no effect on prices, and increases in the variance of the target price can increase average price accuracy, by increasing the returns to informed trading and thereby incentives for traders to become informed.
No, but it's exactly what I was looking for, and surprisingly concise. I'll see if I believe the inferences from the math involved when I take the time to go through it!
Reading "Thinking Fast and Slow" for the first time, and came across an idea that sounds huge if true: that the amount of motivation one can exert in a day is limited. Given the replication crisis, I'm not sure how much credence I should give to this.
A corollary would be to make sure ones non-work daily routines are extremely low willpower when it's important to accomplish a lot during the work day. This flies in the face of other conventional wisdom I've heard regarding discipline, even granting the possibility that the amount of total will-power one can exert over each day can increase with practice.
Anecdotally, my best work days typically start with a small amount of willpower (cold shower night before, waking up early, completing a very short exercise routine, prepping brunch, and biking instead of driving to a library/coffee shop). The people I know who were the best at puzzles and other high effort system-2 activities were the type who would usually complete assignments in school, but never submit their best work.
This hasn't stood up to replication, as you guess. I didn't follow closely, so I'm not sure of the details. Physical energy is certainly limited and affects mental function efficiency. But thinking hard doesnt use measurably more energy than just thinking last I knew. Which sounds at least a little wrong given the subjective experience of really focusing on some types of mental work. I'd guess a small real effect in some circumstances.
Anything written 20 years ago in cognitive science is now antique and needs to be compared against recent research.
It doesn't seem to be true in any literal, biological sense. I don't recall that they had concrete cites for a lot of their theses, and this one doesn't even define the units of measurement (yes, glucose, but no comments about milligrams of glucose per decision-second or anything), so I don't know how you would really test it. I don't think they claim that it's actually fixed over time, nor that you can't increase it with practice and intent.
However, like much of the book, it rings true in a "useful model in many circumstances" sense. You're absolutely right that arranging things to require low-momentary-willpower can make life less stressful and probably get you more aligned with your long-term intent. A common mechanism for this, as the book mentions, is to remove or reduce the momentary decision elements by arranging things in advance so they're near-automatic.
an idea that sounds huge if true: that the amount of motivation one can exert in a day is limited
This is basically the theory that willpower (and ego) are expendable resources that get depleted over time. This was widely agreed upon in the earlier days of LessWrong (although with a fair deal of pushback and associated commentary), particularly as a result of Scott Alexander and his writings (example illustration of his book review on this topic here) on this and related topics such as akrasia and procrastination-beating (which, as you can see from the history of posts containing this tag, were really popular on LW about 12-15 years ago). This 2018 post by lionhearted explicitly mentions how discussions about akrasia were far more prevalent on the site around 2011, and Qiaochu's comments (1, 2) give plausible explanations for why these stopped being so common.
I agree with Seth Herd below that this appears not to have survived the replication crisis. This is the major study that sparked general skepticism of the idea, with this associated article in Slate (both from 2016). That being said, I am not aware of other, more specific or recent details on this matter. Perhaps this 2021 Scott post over on ACX (which confirms that "[these willpower depletion] key results have failed to replicate, and people who know more about glucose physiology say it makes no theoretical sense") and this 2019 question by Eli Tyre might be relevant here.
Little thought experiment with flavors of Newcomb and Berry's Paradox:
I have the code of an ASI in front of me, translated into C along with an oracle to a high-quality RNG. This code is N characters. I want to compete with this ASI at the task of writing a 2N-character C code that halts and prints a very large integer. Will I always win?
Sketch of why: I can write my C code to simulate the action of the ASI on a prompt like "write a 2N-character C code that halts and prints the largest integer" using every combination of possible RNG calls and print the max + 1 or something.
Sketch of why not: The ASI can make us both lose by "intending" to print a non-halting program if it is asked to. There might be probabilistic approaches for the ASI as well, where it produces a non-halting program with some chance. If I can detect this in the simulations, I might be able to work around this and still beat the ASI.
My guess is "no" because both of you would die first. In the context of "largest numbers" 10^10^100 is baby's first step, but is still a number with more digits than you will ever succeed in printing.
In principle the "you" in this scenario could be immortal with unbounded resources and perfect reliability, but then we may as well just suppose you are a superintelligence smarter than the AI in the problem (which isn't looking so 'S' anymore).
To clarify: we are not running any programs, just providing code. In a sense, we are competing at the task of providing descriptions for very large numbers with an upper bound on the size of the description (and the requirement that the description is computable).
Oh, I see that I misread.
One problem is that "every possible RNG call" may be an infinite set. For a really simple example, a binary {0,1} RNG with program "add 1 to your count if you roll 1 and repeat until you roll 0" has infinitely many possible rolls and no maximum output. It halts with probability 1, though.
If you allow the RNG to be configured for arbitrary distributions then you can have it always return a number from such a distribution in a single call, still with no maximum.
Oops, yeah the written programs are supposed to be deterministic. The point of mentioning the RNG was to handle the fact that an AI might derive its performance from a strong random number generator, which a C code can't emulate.
Random thought after reading "A model of UDT with a halting oracle": imagine there are two super-intelligent AIs A and B, suitably modified to have access to their own and each other's source codes. They are both competing to submit a python code of length at most N which prints the larger number, then halts (where N is orders of magnitude larger than the code lengths of A and B). A can try to "cheat" by submitting something like exec(run B on the query "submit a code of length N that prints a large number, then halts") then print(0), but B can do this as well. Supposing they must submit to a halting oracle that will punish any AI that submits a non-halting program, what might A and B do?
Has to be a python code; allowing arbitrary non-computable natural language descriptions gets hairy fast
1
1