Text of post based on our blog post as a linkpost for the full paper which is considerably longer and more detailed.
Neural networks are trained on data, not programmed to follow rules. We understand the math of the trained network exactly – each neuron in a neural network performs simple arithmetic – but we don't understand why those mathematical operations result in the behaviors we see. This makes it hard to diagnose failure modes, hard to know how to fix them, and hard to certify that a model is truly safe.
Luckily for those of us trying to understand artificial neural networks, we can simultaneously record the activation of every neuron in the network, intervene by silencing or stimulating them, and test the network's response to any possible input.
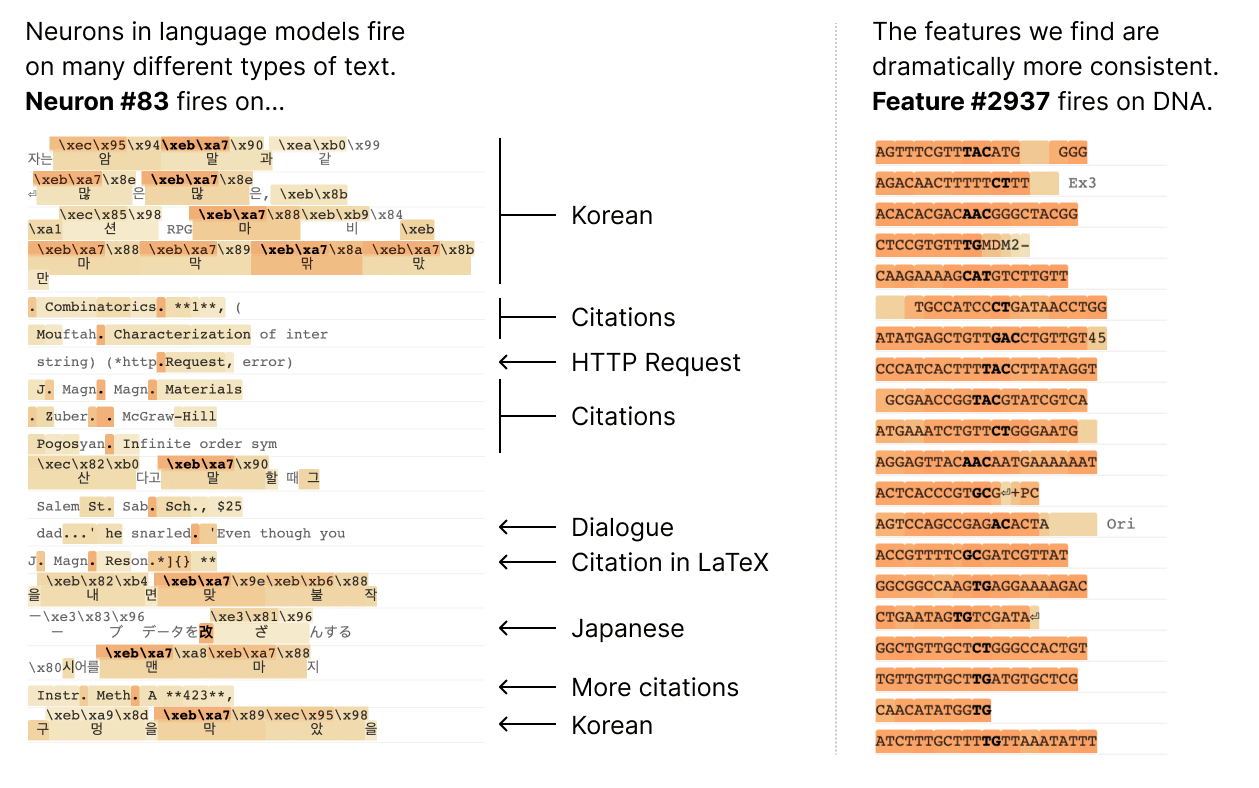
Unfortunately, it turns out that the individual neurons do not have consistent relationships to network behavior. For example, a single neuron in a small language model is active in many unrelated contexts, including: academic citations, English dialogue, HTTP requests, and Korean text. In a classic vision model, a single neuron responds to faces of cats and fronts of cars. The activation of one neuron can mean different things in different contexts.
In our latest paper, Towards Monosemanticity: Decomposing Language Models With Dictionary Learning, we outline evidence that there are better units of analysis than individual neurons, and we have built machinery that lets us find these units in small transformer models. These units, called features, correspond to patterns (linear combinations) of neuron activations. This provides a path to breaking down complex neural networks into parts we can understand, and builds on previous efforts to interpret high-dimensional systems in neuroscience, machine learning, and statistics.
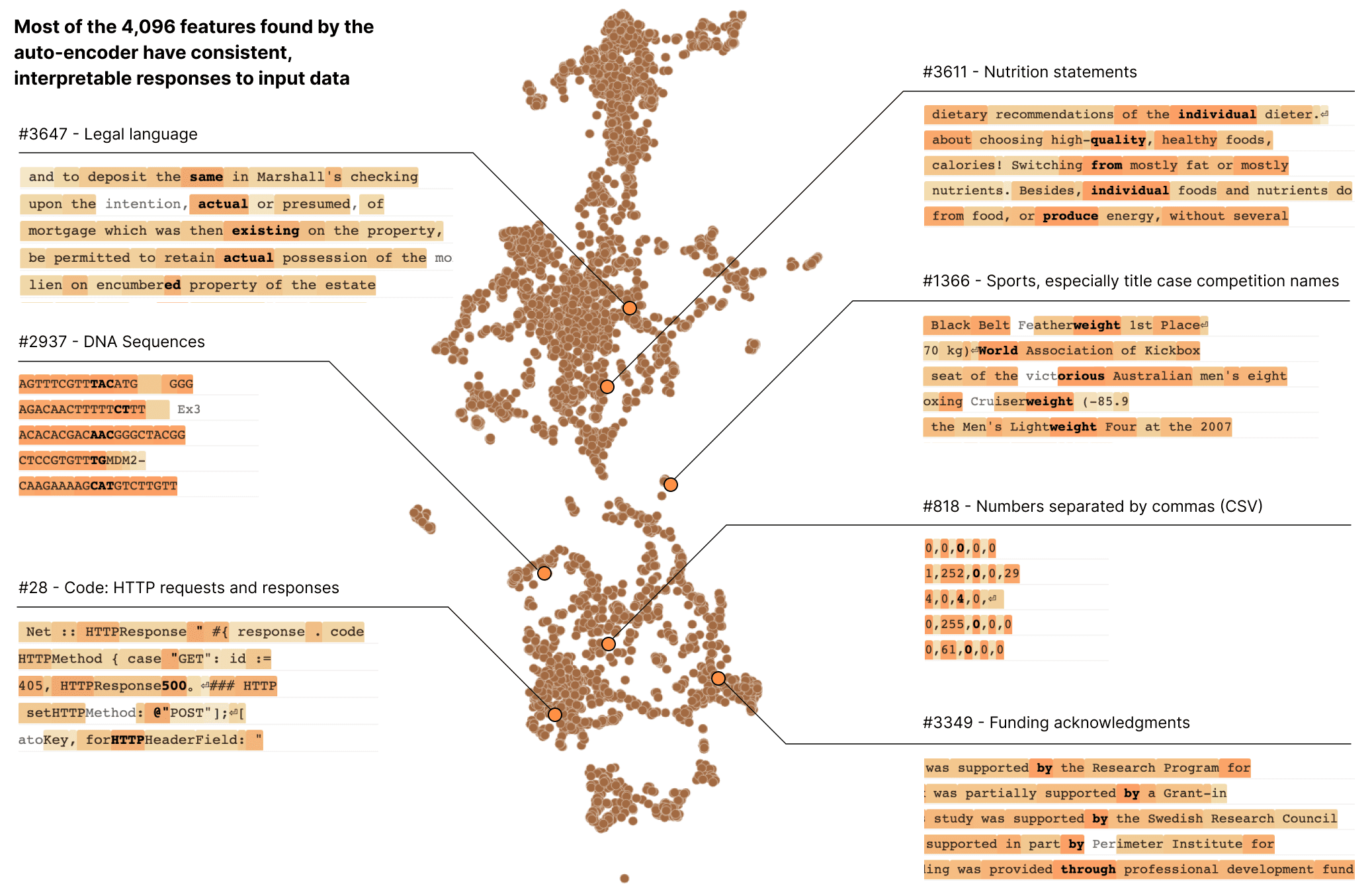
In a transformer language model, we decompose a layer with 512 neurons into more than 4000 features which separately represent things like DNA sequences, legal language, HTTP requests, Hebrew text, nutrition statements, and much, much more. Most of these model properties are invisible when looking at the activations of individual neurons in isolation.
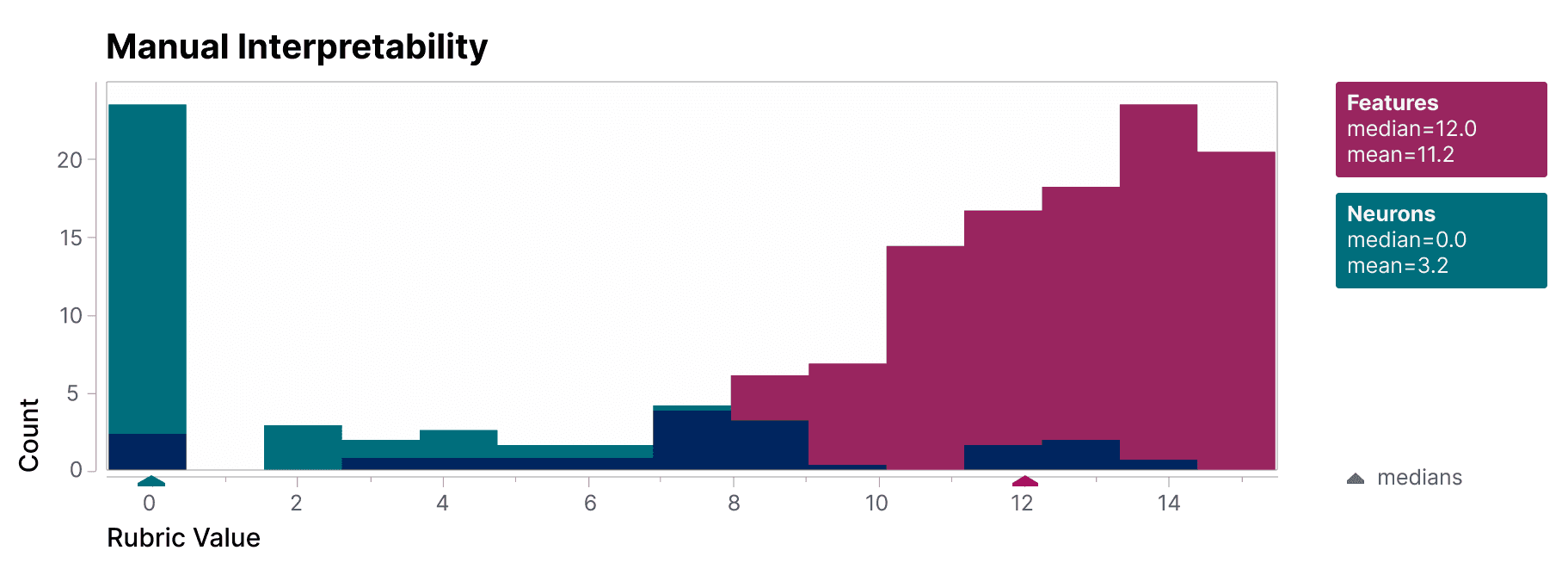
To validate that the features we find are significantly more interpretable than the model's neurons, we have a blinded human evaluator score their interpretability. The features (red) have much higher scores than the neurons (teal).
We additionally take an "autointerpretability" approach by using a large language model to generate short descriptions of the small model's features, which we score based on another model's ability to predict a feature's activations based on that description. Again, the features score higher than the neurons, providing additional evidence that the activations of features and their downstream effects on model behavior have a consistent interpretation.
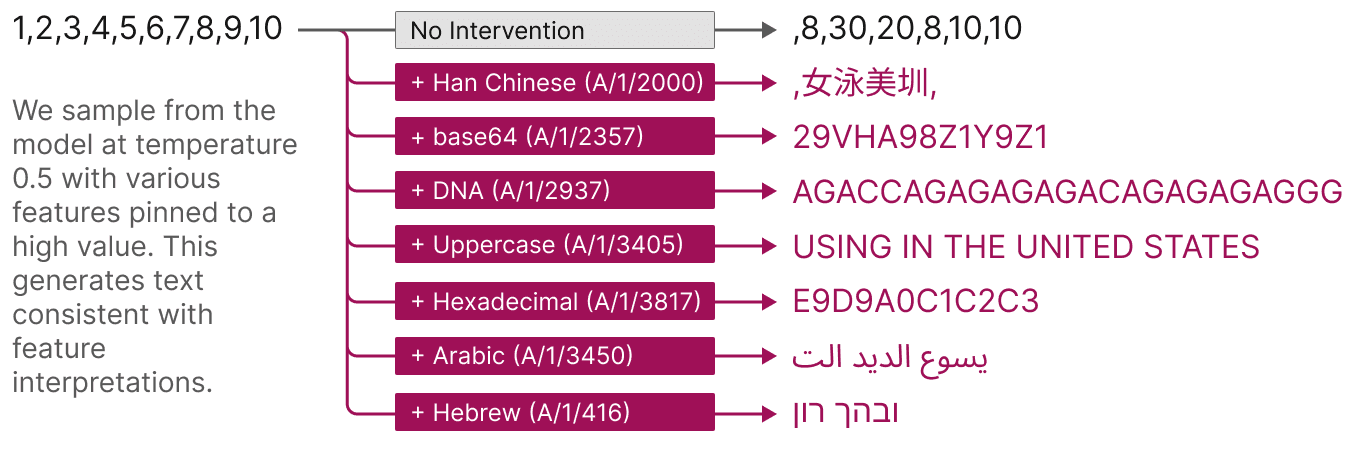
Features also offer a targeted way to steer models. As shown below, artificially activating a feature causes the model behavior to change in predictable ways.
Finally, we zoom out and look at the feature set as a whole. We find that the features that are learned are largely universal between different models, so the lessons learned by studying the features in one model may generalize to others. We also experiment with tuning the number of features we learn. We find this provides a "knob" for varying the resolution at which we see the model: decomposing the model into a small set of features offers a coarse view that is easier to understand, and decomposing it into a large set of features offers a more refined view revealing subtle model properties.
This work is a result of Anthropic’s investment in Mechanistic Interpretability – one of our longest-term research bets on AI safety. Until now, the fact that individual neurons were uninterpretable presented a serious roadblock to a mechanistic understanding of language models. Decomposing groups of neurons into interpretable features has the potential to move past that roadblock. We hope this will eventually enable us to monitor and steer model behavior from the inside, improving the safety and reliability essential for enterprise and societal adoption.
Our next challenge is to scale this approach up from the small model we demonstrate success on to frontier models which are many times larger and substantially more complicated. For the first time, we feel that the next primary obstacle to interpreting large language models is engineering rather than science.
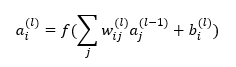
Superposition of features is only advantageous at a certain point in a network when it is followed by non-linear filtering, as explained in Toy Models of Superposition. Yet, this work places the sparse autoencoder at a point in the one-layer LLM which, up to the logits, is not followed by any non-linear operations. Given this, I would expect that there is no superposition among the activations fed to the sparse autoencoder, and that 512 (the size of the MLP output vector) is the maximum number of features the model can usefully represent.
If the above is true, then expansion factors to the sparse representation greater than 1 would not improve the quality or granularity of the 'true' feature representation. The additional features observed would not truly be present in the model's MLP activations, but would rather be an artifact of applying the sparse auto-encoder. Perhaps individual feature interpretability would still improve because the autoencoder could be driven to represent a rotation of the up-to 512 features to a privileged basis via the sparsity penalty. That all said, this work clearly reports various metrics, such as log-likelihood loss reduction, as being improved as the number of sparse feature coefficients expands well beyond 512, which I would think strongly contradicts my point above. Please help me understand what I am missing.
Side note: There is technically a non-linearity after the features, i.e. the softmax operation on the logits (...and layer norm, which I assume is not worth considering for this question). I haven't seen this discussed anywhere, but perhaps softmax is capable of filtering interference noise and driving superposition?
Quotation from Toy Models of Superposition:
"The Saxe results reveal that there are fundamentally two competing forces which control learning dynamics in the considered model. Firstly, the model can attain a better loss by representing more features (we've labeled this "feature benefit"). But it also gets a worse loss if it represents more than it can fit orthogonally due to "interference" between features. In fact, this makes it never worthwhile for the linear model to represent more features than it has dimensions."
Quotation from this work:
"We can easily analyze the effects features have on the logit outputs, because these are approximately linear in the feature activations."
UPDATE: After some more thought, it seems clear that softmax can provide the filtering needed for superposition to be beneficial given a sparse distribution of features. It's interesting that some parts of the LLM model have ReLUs for decoding features, other parts have softmax. I wonder if these two different non-linearities have distinct impacts on the geometries of the over-complete feature basis.