Abstract
This post summarises my findings on the effects of Non-Uniform feature sparsity on Superposition in the ReLU output model, introduced in the Toy Models of Superposition paper, the ReLU output model is a toy model which is shown to exhibit features in superposition instead of a dedicated dimension ('individual neuron') devoted to a single feature. That experiment showed how superposition is introduced in a model by varying the feature sparsity values. However, a uniform sparsity across all the features was considered to keep things interpretable and simple. This post explores the effects of non-uniform sparsity on superposition for a similar experiment setup.
This question was listed in Neel Nanda's 200 Concrete Open Problems in Mechanistic Interpretability post. I've been interested in AI Interpretability for a long time but wasn't sure how to enter the field. I discovered the field of mech-interp recently when I was working on some other project and instantly felt connected to the field. This is my first post on LW and this project is my attempt to increase my comfort working with mech-interp problems and build the necessary reasoning for solving more complex problems.
Introduction
The ReLU output model is a toy model replication of a neural network showcasing the mapping of features (5 input features) to hidden dimensions (2 hidden dimensions) where superposition can be introduced by changing the sparsity of input features. For a set of input features and a hidden layer vector , where , the model is defined as follows:
This model showcases how a large set of input features can be represented in a much smaller dimensional vector in a state of superposition by increasing the sparsity of the input features (sparsity tries to replicate the real-world data distribution where certain concepts are sparsely present throughout the training set). This concept and observations were first introduced in Anthropic's Toy Models of Superposition paper.
Before we go ahead with the analysis, let me give you a primer on some important terms we will encounter in this post:
Feature Importance: Feature importance can be defined as how useful a particular feature is for achieving lower loss.
It's augmented in the ReLU model loss as a coefficient on the weighted mean squared error between the input and the output.
where is the importance of the feature
Feature Sparsity: Feature sparsity is defined by how frequently a feature is present in the input data. In the ReLU Output model, its defined as the probability of the corresponding element in being zero.
An alternate quantity called Feature Probability defined as 1 minus Sparsity is also used in this formulation.
To summarise the paper's findings, it showcases that as we increase the sparsity of input features, more features start getting represented in superposition. When sparsity is high, features of higher importance are represented as a dedicated dimension in the hidden layer, but as we increase the sparsity, lower-importance features start getting represented along with higher-importance features in superposition.
In the below figures, as we move from left to right, feature sparsity is gradually increased showcasing the transition of how more and more features start getting represented in superposition.


I attempt to extend that representation one step further by considering a non-uniform sparsity instead of a uniform sparsity for input features as not all concepts are equally sparse in a training dataset.
Experiment Setup
In my experiment setup, I'm considering two main levers, namely Feature Sparsity and Feature Importance. As we are considering non-uniform sparsity, its combined effect with feature importance plays an important role in the final result and leads to some interesting findings. To showcase different situations, I'm considering four different scenarios:
- Feature with the highest importance has the least sparsity and as we go down feature importance, the sparsity increases
- Feature with the highest importance has the highest sparsity and as we go down feature importance, the sparsity decreases
- Random feature sparsity across features
- Constant feature importance and increasing feature sparsity (similar to Case 1.)
Also, to see the effect of random seed on the final results, every scenario was running eight instances while keeping everything constant.
Note: Similar figures that you will encounter from this point onwards has a slightly different interpretation. All the eight instances in every case have the same distribution of feature sparsity. They are to be interpreted as outputs of different random seeds while every other hyperparameter is kept constant. Feature sparsity is not decreasing as we move from left to right (unlike the preceding figures) in the following figures.
Results
No of Features Represented
In all the scenarios considered with non-uniform sparsity, never once are all the five input features represented in the hidden layer (as we saw in the case of uniform sparsity). No. of feature represented maxes out at 4 and hovers around 3 in a lot of scenarios. The below figure illustrates the phenomena for Case 1, for a detailed view of figures from all the scenarios, refer to this page.

Does this mean that in the case of non-uniform sparsity, all the features will never be represented in the hidden layer and we will always lose some concepts?
To validate this from a different direction, I tried analyzing the number of features represented in a higher hidden dimension (h = 20, no of input features = 80). To estimate the amount of features represented in the hidden layer, I'm choosing the Frobenius Norm as a proxy. The table below summarises the Frobenium Norm values for all the scenarios considered:
We can see, that the Frobenium Norm value in the case of Uniform Sparsity is the highest when compared to all the cases of Non-Uniform Sparsity which indicates the number of features represented when sparsity is uniform will most likely always be higher than when compared to non-uniform sparsity.
| Scenario | Frob Norm |
| Uniform Sparsity (Instance of lowest sparsity) | 7.55 |
| Case 1 (Max of all the instances) | 4.98 |
| Case 2 (Max of all the instances) | 6.6 |
| Case 3 (Max of all the instances) | 5.75 |
| Case 4 (Max of all the instances) | 6.43 |
Effects on Superposition
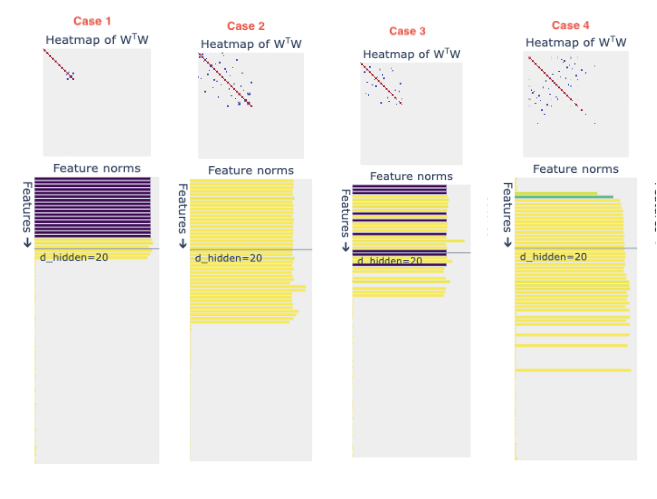
In Case 1, we see the lowest feature representation and the least amount of superposition (showcased in yellow) which was an expected outcome as we are assigning the least amount of sparsity to the most important features. The blanks in the below figure indicate a particular feature is not represented at all in the hidden layer.

Case 2 was pretty interesting as we noticed that all the features represented are always in superposition and none of the features is ever represented as a dedicated dimension irrespective of feature importance.
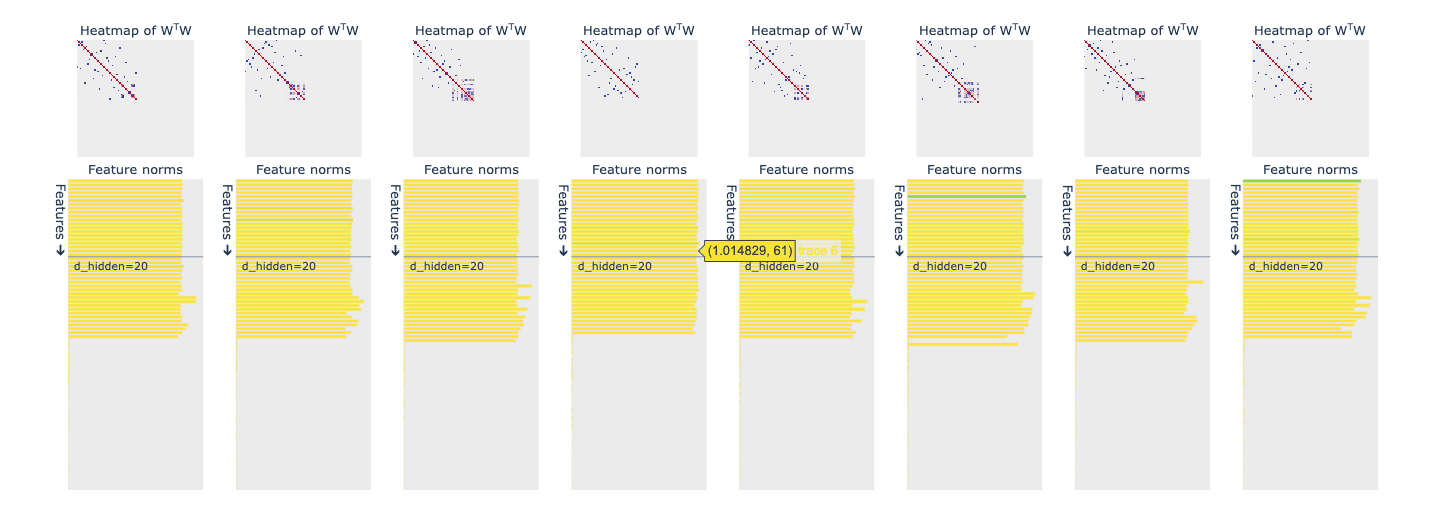
Case 3 is the closest we come to a real-world scenario, where feature sparsity is distributed randomly across features, irrespective of their importance. It looks like an averaged-out scenario of Cases 1 & 2 and strikes an approx. midpoint between dedicated dimensions vs superposition when representing features.
What exact combination of feature sparsity and feature importance governs this behaviour is something I wasn't able to answer in my analysis and I think it'll be an important question to answer as it can help us interpret the feature representations in real-world models.
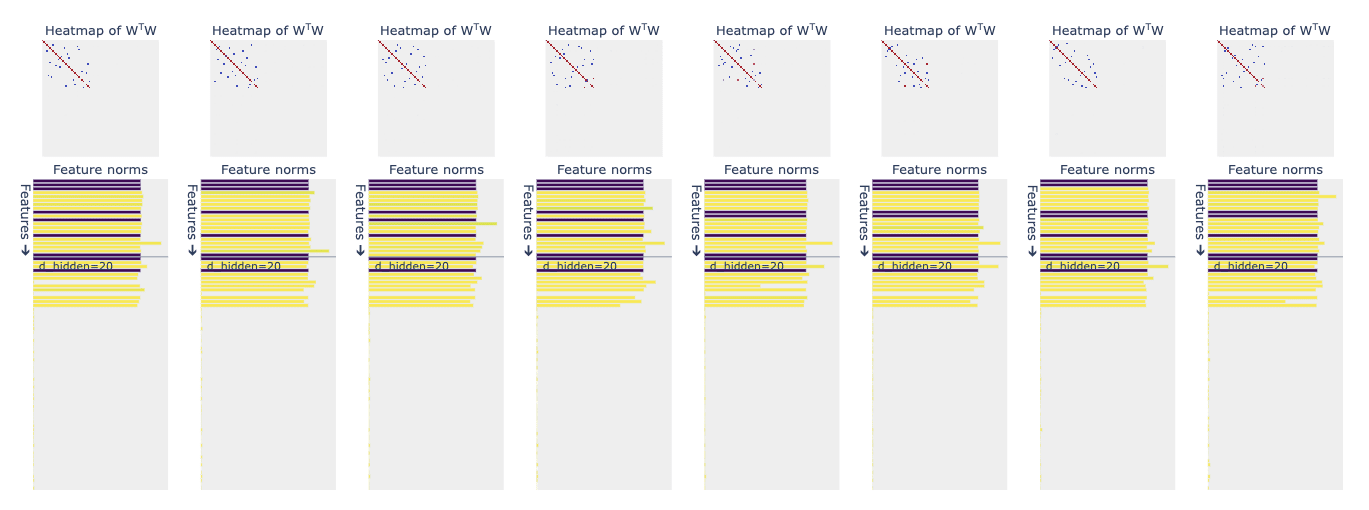
To check a clear effect of sparsity on superposition, we consider Case 4 where we keep the feature importance constant and consider an increasing sparsity (similar to Case 1.)[1]
In this case, we stumble on a weird observation where the few features with the least sparsity are not even learned and represented in the hidden layer. The representation starts after a couple of features where all of the represented features (barring a few exceptions due to random seed) are in superposition all the time.

Presently, I don't have a clear intuition on why this is the case but this is quite a contrary observation compared to my expectation.
Additionally, this scenario also gives us an intuition that feature importance has a bigger contribution in deciding whether a feature is represented as a dedicated dimension or not when compared to sparsity.
This is my first post on LW, so please apologies in case of any deviation from the norm structure of the post and would really appreciate any kind of feedback.
Lastly, I would like to thank @SrGonao for his valuable feedback and a huge shoutout to @CallumMcDougall for creating ARENA. Lots of the code snippets from the course reduced a lot of resistance in my experiment runs.
- ^
We could've considered any pattern for sparsity, this choice was solely because of observational ease.