This relates to costs of compromise!
It's this class of patterns that frequently recur as a crucial considerations in contexts re optimization, and I've been making too many shoddy comments about it. (Recent1[1], Recent2.) Somebody who can write ought to unify the many aspects of it give it a public name so it can enter discourse or something.
In the context of conjunctive search/optimization
- The problem of fully updated deference also assumes a concave option-set. The concavity is proportional to the number of independent-ish factors in your utility function. My idionym (in my notes) for when you're incentivized to optimize for a subset of those factors (rather than a compromise), is instrumental drive for monotely (IDMT), and it's one aspect of Goodhart.
- It's one reason why proxy-metrics/policies often "break down under optimization pressure".
- When you decompose the proxy into its subfunctions, you often tend to find that optimizing for a subset of them is more effective.
- (Another reason is just that the metric has lots of confounders which didn't map to real value anyway; but that's a separate matter from conjunctive optimization over multiple dimensions of value.)
- You can sorta think of stuff like the Weber-Fechner Law (incl scope-insensitivity) as (among other things) an "alignment mechanism" in the brain: it enforces diminishing returns to stimuli-specificity, and this reduces your tendency to wirehead on a subset of the brain's reward-proxies.
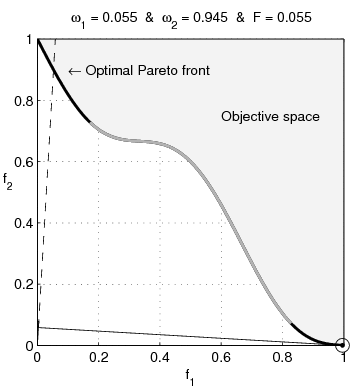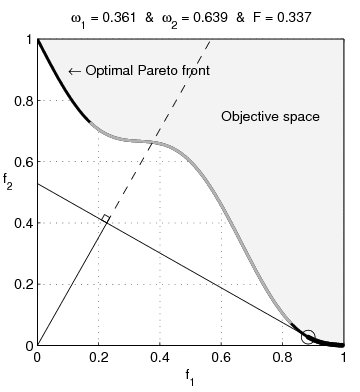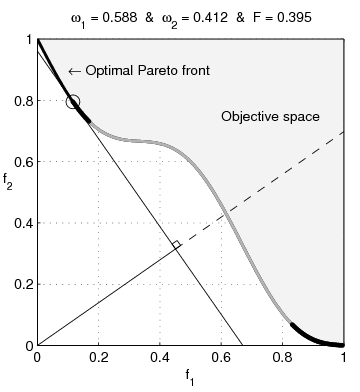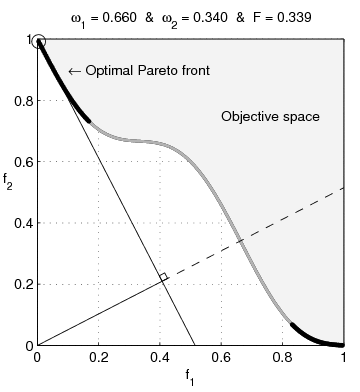
Pareto nonconvexity is annoying
From Wikipedia: Multi-Objective optimization:
Watch the blue twirly thing until you forget how bored you are by this essay, then continue.
In the context of how intensity of something is inversely proportional to the number of options
- Humans differentiate into specific social roles because .
- If you differentiate into a less crowded category, you have fewer competitors for the type of social status associated with that category. Specializing toward a specific role makes you more likely to be top-scoring in a specific category.
- Political candidates have some incentive to be extreme/polarizing.
- If you try to please everybody, you spread out your appeal so it's below everybody's threshold, and you're not getting anybody's votes.
- You have a disincentive to vote for third-parties in winner-takes-all elections.
- Your marginal likelihood of tipping the election is proportional to how close the candidate is to the threshold, so everybody has an incentive to vote for ~Schelling-points in what people expect other people to vote for. This has the effect of concentrating votes over the two most salient options.
- You tend to feel demotivated when you have too many tasks to choose from on your todo-list.
- Motivational salience is normalized across all conscious options[2], so you'd have more absolute salience for your top option if you had fewer options.
I tend to say a lot of wrong stuff, so do take my utterances with grains of salt. I don't optimize for being safe to defer to, but it doesn't matter if I say a bunch of wrong stuff if some of the patterns can work as gears in your own models. Screens off concerns about deference or how right or wrong I am.
I rly like the framing of concave vs convex option-set btw!
- ^
Lizka has a post abt concave option-set in forum-post writing! From my comment on it:
As you allude to by the exponential decay of the green dots in your last graph, there are exponential costs to compromising what you are optimizing for in order to appeal to a wider variety of interests. On the flip-side, how usefwl to a subgroup you can expect to be is exponentially proportional to how purely you optimize for that particular subset of people (depending on how independent the optimization criteria are). This strategy is also known as "horizontal segmentation".
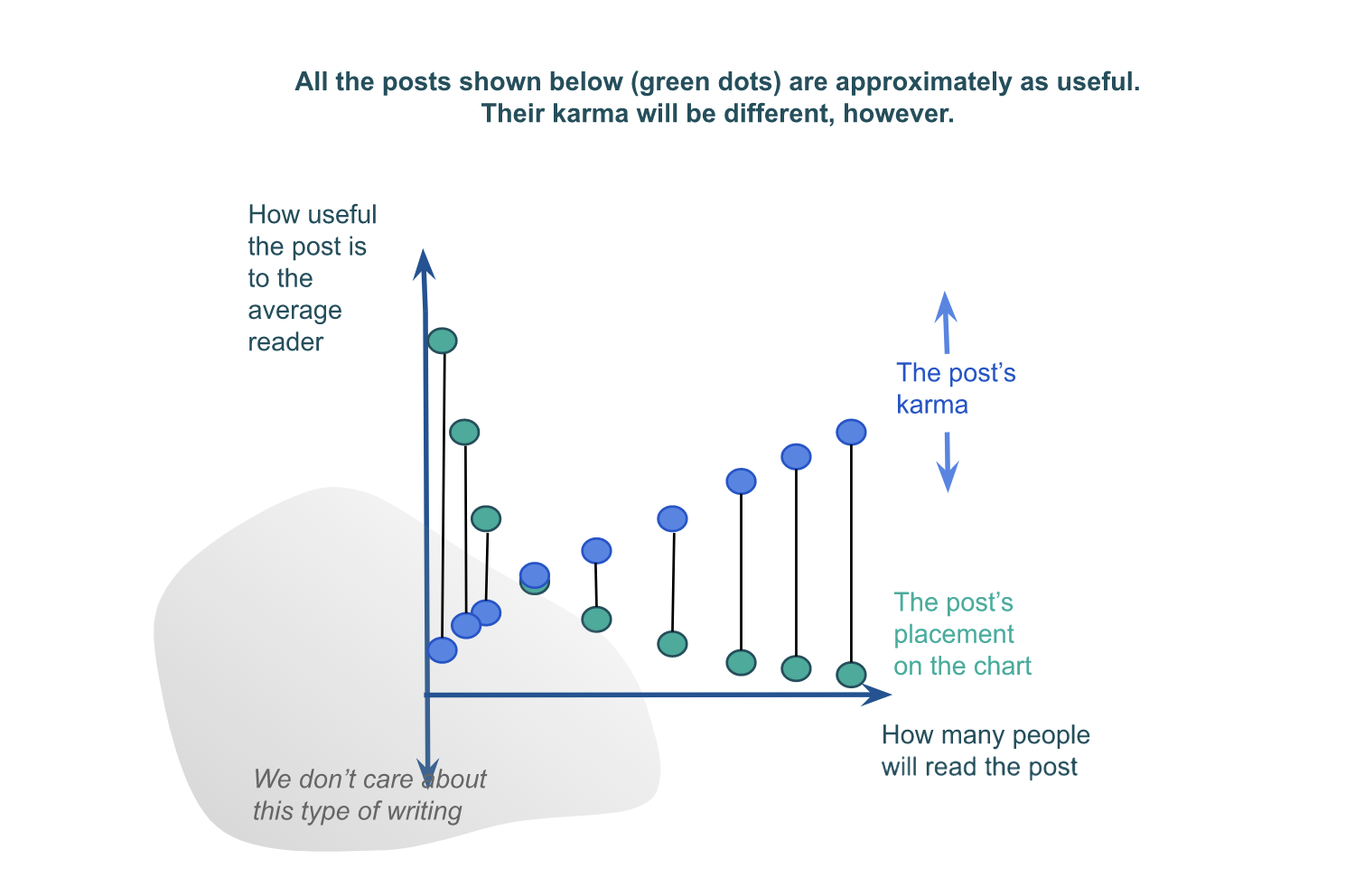
The benefits of segmentation ought to be compared against what is plausibly an exponential decay in the number of people who fit a marginally smaller subset of optimization criteria. So it's not obvious in general whether you should on the margin try to aim more purely for a subset, or aim for broader appeal.
- ^
Normalization is an explicit step in taking the population vector of an ensemble involved in some computation. So if you imagine the vector for the ensemble(s) involved in choosing what to do next, and take the projection of that vector onto directions representing each option, the intensity of your motivation for any option is proportional to the length of that projection relative to the length of all other projections. (Although here I'm just extrapolating the formula to visualize its consequences—this step isn't explicitly supported by anything I've read. E.g. I doubt cosine similarity is appropriate for it.)
I love this comment, and have strong-upvoted it.
I especially enjoy that I seem to have basically popularized a frame you've already been thinking about.
Another aspect of costs of compromise is: How bad is it for altruists to have to compromise their cognitive search between [what you believe you can explain to funders] vs [what you believe is effective]? Re my recent harumph about the fact that John Wentworth must justify his research to get paid. Like what? After all this time, anybody doubts him? The insistence that he explain himself is surely more for show now, as it demonstrates the funders are doing their jobs "seriously".
Related: Eliezer Yudkowsky’s Purchase Fuzzies and Utilons Separately or Alex Lawsen’s Know What You’re Optimizing For. I also note here that you can get concavity via other people picking off the win-win projects in the top right.
I think you can't really assume "that we (for some reason) can't convert between and compare those two properties". Converting space of known important properties of plans into one dimension (utility) to order them and select the top one is how the decision-making works (+/- details, uncertainty, etc. but in general).
If you care about two qualities but really can't compare, even by proxy "how much I care", then you will probably map them anyway by any normalization, which seems most sensible.
Drawing both on a chart is kind of such normalization - you visually get similar sizes on both axes (even if value ranges are different).
If you really cannot convert, you should not draw them on a chart to decide. Drawing makes a decision about how to compare them as there is a comparable implied scale to both. You can select different ranges for axes and the chart will look different and the conclusion would be different.
However, I agree that fat tail discourages compromise anyway, even without that assumption - at least when your utility function over both is linear or similar.
Another thing is that the utility function might not be linear, and even if both properties are not correlated it might make compromises more or less sensible, as applying the non-linear utility function might change the distributions.
Especially if it is not a monotonous function. Like for example you might have some max popularity level that max the utility of your plan choice and anything above you know will make you more uncomfortable or anxious or something (it might be because of other variables that are connected/correlated). This might wipe out fat tail in utility space.
Say that we have a set of options, such as (for example) wild animal welfare interventions.
Say also that you have two axes along which you can score those interventions: popularity (how much people will like your intervention) and effectiveness (how much the intervention actually helps wild animals).
Assume that we (for some reason) can't convert between and compare those two properties.
Should you then pick an intervention that is a compromise on the two axes—that is, it scores decently well on both—or should you max out on a particular axis?
One thing you might consider is the distribution of options along those two axes: the distribution of interventions can be normal on for both popularity and effectiveness, or the underlying distribution could be lognormal for both axes, or they could be mixed (e.g. normal for popularity, and lognormal for effectiveness).
Intuitively, the distributions seem like they affect the kinds of tradeoffs we can make, how could we possibly figure out how?
…
…
…
It turns out that if both properties are normally distributed, one gets a fairly large Pareto frontier, with a convex set of options, while if the two properties are lognormally distributed, one gets a concave set of options.
(Code here.)
So if we believe that the interventions are normally distributed around popularity and effectiveness, we would be justified in opting for an intervention that gets us the best of both worlds, such as sterilising stray dogs or finding less painful rodenticides.
If we, however, believe that popularity and effectiveness are lognormally distributed, we instead want to go in hard on only one of those, such as buying brazilian beef that leads to Amazonian rainforest being destroyed, or writing a book of poetic short stories that detail the harsh life of wild animals.
What if popularity of interventions is normally distributed, but effectiveness is lognormally distributed?
In that case you get a pretty large Pareto frontier which almost looks linear to me, and it's not clear anymore that one can't get a good trade-off between the two options.
So if you believe that heavy tails dominate with the things you care about, on multiple dimensions, you might consider taking a barbell strategy and taking one or multiple options that each max out on a particular axis.
If you have thin tails, however, taking a concave disposition towards your available options can give you most of the value you want.
See Also