When teaching game theory to their novices, microeconomic teachers generally tend to teach simple games. It is common for the student to finish his course learning (or at least supposedly) to deal with matrices of games of the following type:


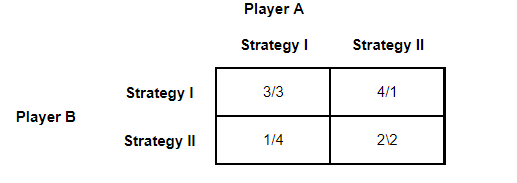
It is expected that every student will be able to solve this type of game when completing their course. What should be noted about this matrix is that it is relatively simple. Yes, dear student, this thing that you suffered so much to solve in your tests is something relatively easy to solve…

The game above is a classic two-player game with two strategies or, as game theorists call it in their incredible creativity, a 2 x 2 game. The incredible ease and unreality of such game is that hardly one person has to deal with just with two strategies. Most of the time people have to deal with more than a couple of choices against a possible opponent. This is where things start to get fun!

When we compute games with more than two strategies the complexities start to appear and the solutions get more complicated. To exemplify my point I will illustrate the case with the simplest game created by humanity: Rock, Paper and Scissors. Everyone has played this game at least once in their lives and don't worry, I'm not going to make a life and death dispute here like in Hunter vs Hunter.

What should be noted about games like Rock, Paper, Scissors is that, first of all, it is a zero-sum game. Either you win or you lose, there is no positive intermediate payoff for the losing player. This feature of the game is very useful for our didactic purposes, as it simplifies our analysis. The second thing to note is that this is obviously a three-strategy game.

3 x 3 games are more complicated to solve than 2 x 2 games. In order not to traumatize you, let's start with an example that is extremely easy to solve. In the matrix below we have a zero-sum game of three strategies:

As this is a zero-sum game and for the sake of simplicity, only the main player's payoffs are computed. Naturally we will start our analysis by looking at whether the game has a saddle-point through a minmax solution. Using this method of resolution we find that:


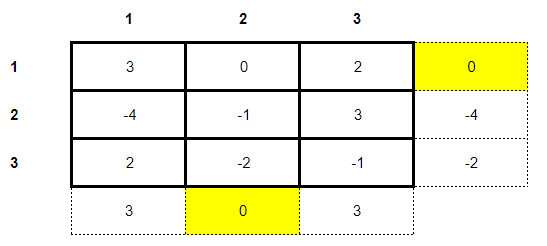
We found a saddle point! The players' optimal strategy in this hypothetical game will be to choose their strategies in such a way that both will end up with a payoff of 0 (a fair game). The value of the game for both players will also be 0, which shows that both will be indifferent whether or not to play the game for the sake of winning.

However, things get more complicated when we analyze the “simple” game of Rock, Paper, Scissors. The matrix of this game is given as follows:


Where the payoffs are given as:

◉ 1 = victory;

◉ 0 = tie;

◉ - 1 = loss

So far a seemingly simple game. As this is a zero-sum game, let's first try to solve it using a minmax. What we found when trying to perform this solution is:


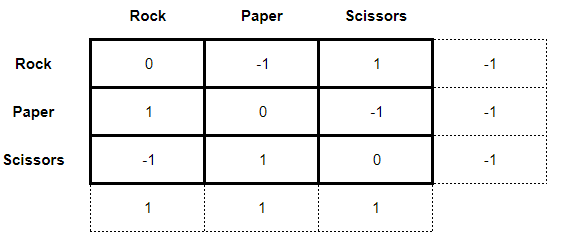
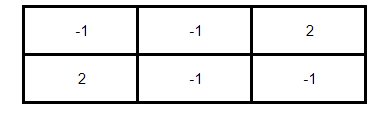
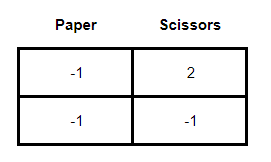
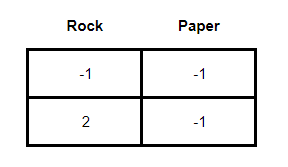
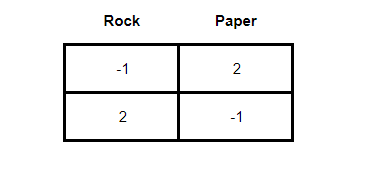
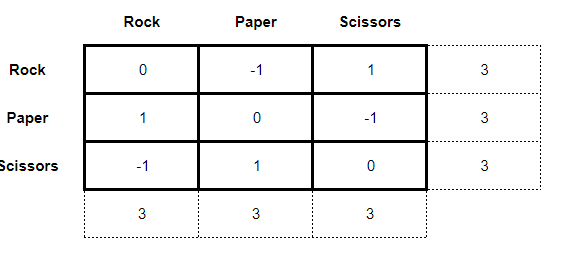
Note that there is no saddle-point for the players, so the minmax solution did not work. When this occurs in zero-sum games, it is necessary to try a mixed strategy solution through dominance. The dominance method consists of comparing, box by box, the payoffs of the players and finding that strategy that presents a better result than the others. When this strategy is found, for the case of the main player, the dominated strategies are excluded from the matrix or, for the case of the rival player, the dominant strategies. As a result, we have a simplification of the game matrix from a 3 x 3 to a 2 x 2 or a 2 x n. It makes it easier for the student to answer.

However, in the case of Rock, Paper, Scissors, this is not a possible solution. Note, dear reader, that there is no dominance in the matrix above, as the comparison cell by cell does not reveal any strategy superior to the others (in fact, the strategies are symmetric!). Well, in that case we will have to resort to a much more exotic method of solving games that I will teach you below…


To solve the game below, we first have to subtract the first line or the first column from the following lines and columns, depending on whether we are analyzing the game from the point of view of the main player (columns) or the rival player (lines). Let's imagine that we are the main player and we are trying to analyze the possible strategies of the rival. In this case, the first step in solving the game involves subtracting the lines from the immediately following lines, obtaining the matrix below:


What we do next is calculate the odds for each strategy. To do this we choose between the three strategies (Rock, Paper or Scissors) and isolate the one we are analyzing. If we are analyzing the odds of the “Rock” strategy, then we would have the following simplification of the matrix above:

Then we multiply the payoffs diagonally and subtract them. Doing this for the above example of the “Rock” strategy we would have:

                                                       (-1) x (-1) - ((-1) x 2) = 3

Thus, the chances of the “Rock” strategy would be equal to 3. Doing the same for “Scissors” we have:

                                                       (-1) x (-1) - ((-1) x 2) = 3

And for “Paper”:


(-1) x (-1) - 2 x 2 = -3

Since the odds cannot be negative, we can disregard the -3 sign and compute it as 3. Thus the odds of the rival player's strategies are 3:3:3. However, dear reader, remember that the strategies of Rock, Paper, Scissors players are symmetrical. Thus, the odds for the main player's strategies are also 3:3:3. This way we can compute the odds in our game matrix as:

Note, dear reader, that we can simplify this matrix even more. The odds can be simplified given that they have a common multiplier (3). Carrying out the division we have that the chances of each player will be 1:1:1.

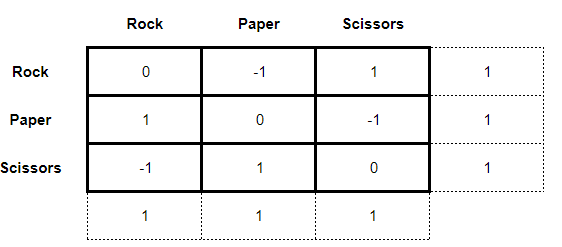
Thus, each player will have to combine their strategies according to the odds of 1:1:1. In other words, their rational choice will be to use… any one of the strategies! There is no clear answer to what the strategy adopted by the player should be. Not strangely if we calculate the value of this game for any of the players we will have:

                                                     (1 x 0) + (1 x -1) + (1) / 3 = 0

A average payoff of the game is 0 and therefore a fair game for both players (nobody loses and nobody wins on average).

The big issue with Rock, Paper, Scissors (apart from the solution) is that any change in the odds of one of the players can affect the value of the game. As a recent post noted, if one of the players has a better chance than the other on one of the strategies (whether he makes a poker face or deters his opponent) then the game is unbalanced; with the player improving his payoff but making the game less interesting to play at the same time!