Regarding the more general question of "how much should interpretability make reference to the data distribution?", here are a few thoughts:
Firstly, I think we should obviously make use of the data distribution to some extent (and much of my work has done so!). If you're trying to reverse engineer a regular computer program, it's extremely useful to have traces of that program running. So too with neural networks!
However, the fundamental thing I care about is understanding whether models will be safe off-distribution, so an understanding which is tied to a specific distribution – and especially to a narrow distribution – is less clear in how it advances my core goals. Explanations which hold narrowly but break off distribution are one of my biggest worries for interpretability, and a big part of why I've taken the mechanistic approach rather than picking low-hanging fruit in correlational interpretability. I'm much more worried about explanations only holding on narrow distributions than I am about incomplete global explanations -- this is probably a significant implicit motivator of my research taste. (Caveat: I'm reluctantly okay with certain aspects of understanding being built on the entire training distribution when we have a compelling theoretical argument for why this captures everything and will generalize.)
Let's return to my example of protein binding affinities from my other comment and imagine two different descriptions of the situation:
- The "global story" – We have a table of binding affinities. When one protein has a much higher binding affinity than the other, it outcompetes it.
- The "on distribution story" – We have a table of proteins which "block" other proteins in practice.
The global story is a kind of "unbiased account of the mechanism" which requires us to think through more possibilities, but can predict weird out of distribution behavior. On the other hand, the "on distribution story" highlights the aspects of the mechanism which are important in practice, but might fail in weird situations.
But what do we want from the on-distribution analysis?
One easy answer is that we just want to use it to make mechanistic understanding easier. Neural networks are immensely complicated computer programs. It seems to me that even understanding small neural networks is probably comparable to something like "reverse engineer a compiled linux kernel knowing nothing about operating systems". It's very helpful to have examples of it running to kind of bootstrap your analysis.
But I think there's something deeper which you're getting at, which I might articulate as distinguishing which aspects of a neural network's mechanistic behavior are "deliberate or useful" and which are "bugs or quirks". For example, in the framework paper we highlight some skip-trigrams which appear to be bugs:
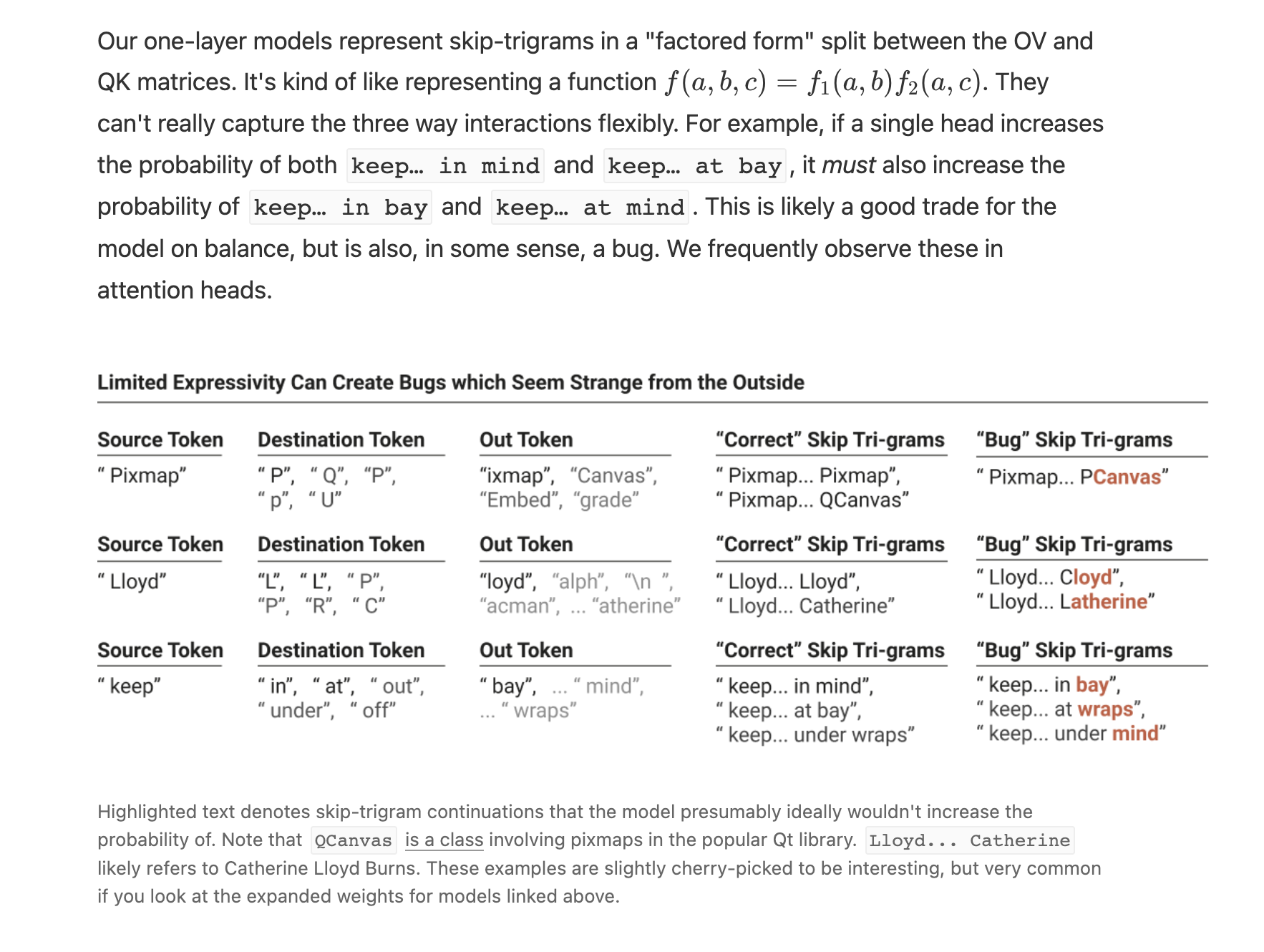
Of course, distinguishing between "correct" skip tri-grams and "bug" skip-trigrams required our judgment based on understanding the domain. In an impartial account of the mechanism, they're all valid skip-trigrams the model implements. It's only with reference to the training distribution or some other external distribution or task that we can think of some as "correct" and others as "bugs".
By more explicitly analyzing on a distribution, one might automate this kind of differentiation. And possibly, one might just ignore these (especially to the extent that other heads or the bigrams can compensate in practice!). This could make a simpler "explanation" at the cost of not generalizing to other distributions.
(In this particular case, I suspect there might actually be a more beautiful, non-distribution specific story to be told in terms of superposition. But that's another topic.)
One interesting thing this suggests is that a "global story" should be able to be "bound" to a distribution to create an in-distribution account. For example, if one has a list of binding affinities for different chemicals, and knows that only a certain subset will be present at the same time, one can produce a summary of which will block each other.
While we're on the topic, it's perhaps useful to more directly describe my concerns about distribution-specific understanding of models, and especially narrow-distribution understanding of the kind a lot of work building Causal Scrubbing seems to be focusing on.
It seems to me that this kind of work is very vulnerable to producing fragile understandings of models which break on a wider distribution due to interpretability illusion type issues.
As one concrete example from my own experience, in the early days of Anthropic I looked into how language models perform arithmetic by only looking at model behavior only on arithmetic expressions. Immediately, lots of interesting patterns popped out and some interesting partial stories began to emerge. However, as soon as I returned to the full training distribution, the story fell apart. All the components I thought did something were doing other things – often primarily doing other things – on the full distribution. Of course, this was a very casual investigation and not anywhere near as rigorous as the causal scrubbing work. But while I'm sure there were ways my understanding on distribution was incomplete, I'm 100x more worried about the fact that it was clearly misleading about the general situation. (My strong suspicion is that there is a very nice story here, but it's deeply intertwined with superposition and we can't understand it without addressing that.)
With that said, I'm very excited for people to be taking different approaches to these problems. My concerns could be misplaced! I definitely think that restricting to a narrow distribution allows one to make a lot of progress on that type of understanding.
I’m sympathetic to many of your concerns here.
It seems to me like the induction head mechanism as described in A Mathematical Framework is an example of just looking at what a part of a model does on a particular distribution, given that those heads also do some unspecified amount of non-induction behaviors with non-induction mechanisms, as eg discussed here https://www.alignmentforum.org/posts/Si52fuEGSJJTXW9zs/behavioral-and-mechanistic-definitions-often-confuse-ai . (Though there’s a big quantitative difference—the distribution where induction happens is way bigger than eg the distribution where IOI happens.) Do you agree?
I moderately disagree with this? I think most induction heads are at least primarily induction heads (and this points strongly at the underlying attentional features and circuits), although there may be some superposition going on. (I also think that the evidence you're providing is mostly orthogonal to this argument.)
I think if you're uncomfortable with induction heads, previous token heads (especially in larger models) are an even more crisp example of an attentional feature which appears, at least on casual inspection, to typically be monosematnically represented by attention heads. :)
As a meta point – I've left some thoughts below, but in general, I'd rather advance this dialogue by just writing future papers.
(1) The main evidence I have for thinking that induction heads (or previous token heads) are primarily implementing those attentional features is just informally looking at their behavior on lots of random dataset examples. This isn't something I've done super rigorously, but I have a pretty strong sense that this is at least "the main thing".
(2) I think there's an important distinction between "imprecisely articulating a monosemantic feature" and "a neuron/attention head is polysemantic/doing multiple things". For example, suppose I found a neuron and claimed it was a golden retriever detector. Later, it turns out that it's a U-shaped floppy ear detector which fires for several species of dogs. In that situation, I would have misunderstood something – but the misunderstanding isn't about the neuron doing multiple things, it's about having had an incorrect theory of what the thing is.
It seems to me that your post is mostly refining the hypothesis of what the induction heads you are studying are – not showing that they do lots of unrelated things.
(3) I think our paper wasn't very clear about this, but I don't think your refinements of the induction heads was unexpected. (A) Although we thought that the specific induction head in the 2L model we studied only used a single QK composition term to implement a very simple induction pattern, we always thought that induction heads could do things like match [a][b][c]. Please see the below image with a diagram from when we introduced induction heads that shows richer pattern matching, and then text which describes the k-composition for [a][b] as the "minimal way to create an induction head", and gives the QK-composition term to create an [a][b][c] matching case. (B) We also introduced induction heads as a sub-type of copying head, so them doing some general copying is also not very surprising – they're a copying head which is guided by an induction heuristic. (Just as one observes "neuron splitting" creating more and more specific features as one scales a model, I expect we get "attentional feature splitting" creating more and more precise attentional features.)

(3.A) I think it's exciting that you've been clarifying induction heads! I only wanted to bring these clarifications up here because I keep hearing it cited as evidence against the framework paper and against the idea of monosemantic structures we can understand.
(3.B) I should clarify that I do think we misunderstood the induction heads we were studying in the 2L models in the framework paper. This was due to a bug in the computation of low-rank Frobenius norms in a library I wrote. This is on a list of corrections I'm planning to make to our past papers. However, I don't think this reflects our general understanding of induction heads. The model was chosen to be (as we understood it at the time) the simplest case study of attention head composition we could find, not a representative example of induction heads.
(4) I think attention heads can exhibit superposition. The story is probably a bit different than that of normal neurons, but – drawing on intuition from toy models – I'm generally inclined to think: (a) sufficiently important attentional features will be monosemantic, given enough model capacity; (b) given a privileged basis, there's a borderline regime where important features mostly get a dedicated neuron/attention head; (c) this gradually degrades into being highly polysemantic and us not being able to understand things. (See this progression as an example that gives me intuition here.)
It's hard to distinguish "monosemantic" and "slightly polysemantic with a strong primary feature". I think it's perfectly possible that induction heads are in the slightly polysemantic regime.
(5) Without prejudice to the question of "how monosemantic are induction heads?", I do think that "mostly monosemantic" is enough to get many benefits.
(5.A) Background: I presently think of most circuit research as "case studies where we can study circuits without having resolved superposition, to help us build footholds and skills for when we have". Mostly monosemantic is a good proxy in this case.
(5.B) Mostly monosemantic features / attentional features allow us to study what features exist in a model. A good example of this is the SoLU paper – we believe many of the neurons have other features hiding in correlated small activations, but it also seems like it's revealing the most important features to us.
(5.C) Being mostly monosemantic also means that, for circuit analysis, interference with other circuits will be mild. As such, the naive circuit analysis tells you a lot about the general story (weights for other features will be proportionally smaller). For contrast, compare this to a situation where one believes they've found a neuron (say a "divisible by seven" number detector, continuing my analogy above!) and it turns out that actually, that neuron mostly does other things on a broader distribution (and they even cause stronger activations!). Now, I need to be much more worried about my understanding…
(I also think that the evidence you're providing is mostly orthogonal to this argument.)
Upon further consideration, I think you're probably right that the causal scrubbing results I pointed at aren't actually about the question we were talking about, my mistake.
but in general, I'd rather advance this dialogue by just writing future papers
Seems like probably the optimal strategy. Thanks again for your thoughts here.
(Context, I work at Redwood)
While we're on the topic, it's perhaps useful to more directly describe my concerns about distribution-specific understanding of models, and especially narrow-distribution understanding of the kind a lot of work building Causal Scrubbing seems to be focusing on.
Can I summarize your concerns as something like "I'm not sure that looking into the behavior of "real" models on narrow distributions is any better research than just training a small toy model on that narrow distribution and interpreting it?" Or perhaps you think it's slightly better, but not considerably?
If so, I mostly agree --- it doesn't very clear this is much better. I'm something like into:
- Picking a distribution
- Training a model to perform well on that distribution
- Interpreting the model (or parts of the model, etc)
as a default interpretability workflow.
For instance, it's not very clear to me that IOI is much more interesting that just training a model on some version of the IOI distribution and then interpreting that model. And I think a key problem with IOI is that the model doesn't really care very much about doing well on this exact task: after having skimmed though copious amounts[1] of OpenWebText, the IOI task as exactly formulated seems pretty non-central IMO.
There are various arguments for looking into narrow examples IMO, but the case is a bit more subtle. (For instance it seems like we should ideally be able to answer questions like 'why did this model have strange behavior in this narrow distribution' where the 'why' will probably have to make reference to how the model behaves on a broader distribution of interest)
It's also possible we disagree about how useful it is to do interpretability on toy tasks. I'm not really sure if there's anything interesting and quick to say here.
I've perhaps skimmed somewhere between 10,000 to 100,000 passages? (I haven't counted) ↩︎
Can I summarize your concerns as something like "I'm not sure that looking into the behavior of "real" models on narrow distributions is any better research than just training a small toy model on that narrow distribution and interpreting it?" Or perhaps you think it's slightly better, but not considerably?
Between the two, I might actually prefer training a toy model on a narrow distribution! But it depends a lot on exactly how the analysis is done and what lessons one wants to draw from it.
Real language models seem to make extensive use of superposition. I expect there to be lots of circuits superimposed with the one you're studying, and I worry that studying it on a narrow distribution may give a misleading impression – as soon as you move to a broader distribution, overlapping features and circuits which you previously missed may activate, and your understanding may in fact be misleading.
On the other hand, for a model just trained on a toy task, I think your understanding is likely closer to the truth of what's going on in that model. If you're studying it over the whole training distribution, features either aren't in superposition (there's so much free capacity in most of these models this seem possible!) or else they'll be part of the unexplained loss, in your language. So choosing to use a toy model is just a question of what that model teaches you about real models (for example, you've kind of side-stepped superposition, and it's also unclear to what extent the features and circuits in a toy model represent the larger model). But it seems much clearer what is true, and it also seems much clearer that these limitations exist.
Thanks for writing this up. It seems like a valuable contribution to our understanding of one-layer transformers. I particularly like your toy example – it's a good demonstration of how more complicated behavior can occur here.
For what it's worth, I understand this behavior as competition between skip-trigrams. We introduce "skip-trigrams" as a way to think of pairs of entries in the OV and QK-circuit matrices. The QK-circuit describes how much the attention head wants to attend to a given token in the attention softmax and implement a particular skip-trigram. The phenomenon you describe occurs when there are multiple skip-trigrams present with different QK-circuit values.
An analogy I find useful for thinking about this is protein binding affinity in molecular biology. (I don't know much about molecular biology – hopefully experts can forgive me if my analogy is naive!) Proteins have a propensity to bind to other proteins, just as attention heads have a propensity to attend between specific tokens and implement skip-trigrams. However, fully understanding the behavior requires remembering that when one protein has a higher binding affinity than another, it can "block" binding. This doesn't mean that it's incorrect to understand proteins as having binding affinity! Nor does it mean that skip-trigrams are the wrong way to understand one-layer models. It just means that in thinking about proteins (or skip-trigrams) one wants to keep in mind the possibility of second order interactions.
I do think your example is very clarifying about the kind of second order interactions that can occur with skip-trigrams! While I definitely knew "skip-trigrams compete for attention", I hadn't realized it could give rise to this behavior.
With that said, I get the sense that maybe you might have understood us to be making a stronger claim about skip-trigrams being independent which we didn't intend. I'm sorry for any confusion here. We do talk about "independent skip-trigram models". Here "independent" is modifying "models" – it's referring to the fact that there are multiple attention heads implementing independent skip-trigram models. (This might seem trivial now, but we had spent an entire section on this point because many people didn't realize this from the original concatenated version of the transformer equations.) Then "skip-trigram" is referring to the fact that the natural units of one-layer models are triplets of tokens. Although our introduction and section introduce this without more context, our actual discussion of skip-trigrams keeps referring back to the OV and QK-circuits, which is the mathematical model they're trying to provide a language for talking about.
I've been meaning to add a number of correctives and clarifications to our papers – this is on the list, and we'll link to your example!
(I'll comment on your more general thesis regarding understanding models with respect to a specific distribution in a separate comment.)
Thanks for this post! I'm not sure how much I expect this to matter in practice, but I think that the underlying point of "sometimes the data distribution matters a lot, and ignoring it is suspect" seems sound and well made.
I personal think it's clear that 1L attn-only models are not literally just doing skip trigrams. A quick brainstorm of other things I presume they're doing:
- Skip trigrams with positional decay - it's easy enough to add a negative term to the attention scores that gets bigger the further away the source token is. For skip trigrams like "keep ... in -> mind" that clearly want to be trigrams, it seems like this has to be going on. You can mediate it with a high BOS attention, so it doesn't attend locally when no skip trigram fires
- Hierarchical skip trigrams (somewhat like your example) - if skip trigram 1 triggers, it stops skip trigram 2 from triggering.
- Dealing with the level of saturation - for a trigram A ... B -> C, it's unclear what happens if there are multiple copies of A, and the model can choose how to mediate this.
- Toy example - let's say attention to A and to BOS are all that matters (everything else is -1000). If BOS is 0 and A is 10, then the model doesn't care if there are multiple As, it saturates immediately. If BOS is 5 and A is 0, then it's now basically linear in the number of As. (In practice I expect it'll be somewhere in the middle)
- "context detection" - text tends to cluster into different contexts (books, wikipedia, etc), which have very different unigram and bigram statistics, and a model could learn to do the correct unigram updates for any destination token, conditional on a bunch of relevant source tokens being there.
- There are probably some tokens that are way more common in some contexts than others (" yield", " return", "\n\t\t" in Python code, etc), and a model could learn skip trigrams from any dest token to these source tokens (probably implemented via the query bias), whose OV circuit just boosts the unigram direction.
- In some sense this is an ensemble of skip trigrams, I think it's different because the natural way to implement it is to have the total attention paid to the special tokens saturate at uniform beyond a certain threshold of possible source tokens
- Skip bigrams - when there's a previous token head that acts semi-independently of the destination token, to implement A __ -> C behaviour. I expect this arises for eg can|'t| vs don|'t|, where the previous token significantly disambiguates the current token.
Worth noting that both some of Anthropic's results and Lauren Greenspan's results here (assuming I understand her results correctly) give a clear demonstration of learned (even very toy) transformers not being well-modeled as sets of skip trigrams.
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2024. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
I don’t completely follow what you mean by data distribution dependence. We can still talk about the function implemented by a transformer in a data distribution independent way, but in general this function might be quite complicated. Should I understand that we can usually simplify the description of the function if we take the data distribution into account?
(thanks to Tao Lin and Ryan Greenblatt for pointing this out, and to Arthur Conmy, Jenny Nitishinskaya, Thomas Huck, Neel Nanda, and Lawrence Chan, Ben Toner, and Chris Olah for comments, and many others for useful discussion.)
In “A Mathematical Framework for Transformer Circuits”, Elhage et al write (among similar sentences):
When I first read this, I (and at least some other readers) interpreted this as a mathematical claim–that the attention layer of a one-layer transformer can be mathematically rewritten as a set of skip-trigrams, and that you can understand the models by reading these skip-trigrams off the model weights (and also reading the bigrams off the embed and unembed matrices, as described in the zero-layer transformer section – I agree with this part).
But this mathematical claim is false: One-layer transformers are more expressive than skip-trigrams, so you can’t understand them by transforming them into a set of skip-trigrams. Also, even if a particular one-layer transformer is actually only representing skip-trigrams and bigrams, you still can’t read these off the weights without reference to the data distribution.
The difference between skip-trigrams and one-layer transformers is that when attention heads attend more to one token, they attend less to another token. This means that even single attention heads can implement nonlinear interactions between tokens earlier in the context.
In this post, I’ll demonstrate that one-layer attention-only transformers are more expressive than a set of skip-trigrams, then I’ll tell an intuitive story for why I disagree with Elhage et al’s claim that one-layer attention-only transformers can be put in a form where “all parameters are contextualized and understandable”.
(Elhage et al say in a footnote, “Technically, [the attention pattern] is a function of all possible source tokens from the start to the destination token, as the softmax calculates the score for each via the QK circuit, exponentiates and then normalizes”, but they don’t refer to this fact further.)
An example of a task that is impossible for skip-trigrams but is expressible with one-layer attention-only transformers
Consider the task of predicting the 4th character from the first 3 characters in a case where there are only 4 strings:
So the strings are always:
This can’t be solved with skip-trigrams
A skip-trigram (in the sense that Elhage et al are using it) looks at the current token and an earlier token and returns a logit contribution for every possible next token. That is, it’s a pattern of the form
………….X……………………Y -> Z
where you update towards or away from the next token being Z based on the fact that the current token is Y and the token X appeared at a particular location earlier in the context.
(Sometimes the term “skip-trigram” is used to include patterns where Y isn’t immediately before Z. Elhage et al are using this definition because in their context of autoregressive transformers, the kind of trigrams that you can encode involve Y and Z being neighbors.)
In the example I gave here, skip-trigrams can’t help, because the probability that the next token after Q is T is 50% after conditioning on the presence of any single earlier token.
This can be solved by a one-layer, two-headed transformer
We can solve this problem with a one-layer transformer with two heads.
The first attention head has the following behavior, when attending from the token Q (which is the only case we care about):
So it attends almost entirely to B if B is present. If B isn’t present (because the first character was A), it will attend almost entirely to C or D. If it attends to C, it writes T; if it attends to D, it writes F. This head therefore writes the correct answer in cases where the first character was A, and writes nothing otherwise.
(By “OV behavior”, I mean W_U W_{OV} embed. So e.g. I’m saying that if you take the embedding for C, then multiply it by this head’s OV, and then unembed that, you’ll get a vector which is in the direction of the unembed for T.)
The second attention head handles the case where the first character was B:
It’s impossible for an ensemble of skip-trigrams to learn this task, if by “ensemble of skip-trigrams” you mean “a logistic regression where all the features are of the form (token A was at position P and token B is at the current position)”, which is the most reasonable interpretation of how transformers could be considered as a set of skip-trigrams.
Proof sketch: Logistic regressions can only perfectly solve classification problems if there’s a hyperplane separating positive and negative examples. In this case, we’re only able to use the skip-trigrams that tell us whether A or B was at the first position and whether C or D was at the second position. A is only present if B isn’t present, so we only need to have one feature that represents the token at the first position; likewise for C and D. So we’re now considering the logistic regression with two features: “is A at the first position” and “is C at the second position”. It’s impossible to separate the two classes for the usual reason that you can’t learn xor with logistic regression. (Bigrams don’t help in this case because for every input, the current token is Q.) (Thanks to Paul Christiano for help with this proof.) This establishes that one-layer transformers cannot be rewritten as sets of bigrams and skip-trigrams.
In this case, the problem could have been solved if the model could express skip-quadgrams. However, we can construct similar problems that one-layer attention-only transformers can solve that skip-quadgrams can’t. (More generally, because softmax induces a nonlinear infinite-order interaction between all the attention scores, for any fixed n, one-layer attention-only transformers (with an unlimited number of heads and an unlimited vocab size) can express functions that ensembles of skip-n-grams can’t.
(One-layer attention-only transformers can express functions that can’t be expressed by skip-n-grams even if they only have a single attention head. I used multiple attention heads in this example because it allowed me to express xor, which is a particularly clean example of a function that skip-trigrams can’t model at all.)
I think that this transformer is probably pretty easy for SGD to learn–it’s not just a pathological counterexample.
IMO, for reasonable definitions of “understanding”, this falsifies Elhage et al’s claim that you can understand the one-layer transformer from its weights
Elhage et al write:
I disagree that they have put their one-layer transformers into a form where all parameters are contextualized and understandable.
To me, what it means to say that a parameter is contextualized and understandable is that you can understand “what role the parameter plays” without learning more about the other parameters or the data distribution. This isn’t true in the example transformer I described above–in both of the heads, you couldn’t really understand why a single attention score had the value it had without looking at the others.
Here’s an intuitive example of how this might come up in a real language model. (I’m not saying that this is actually the best way for the language model to solve the problem I describe, but I am saying that I’m not comfortable assuming this mechanism away without empirical evidence.) Suppose your model has a head that primarily has the responsibility of looking at nouns that appear in news articles and then suggesting related nouns. This head might not do anything on sequences that aren’t news articles (because some of the skip-trigrams it implements are only valid in the context of news articles and not in e.g. Python source files, even though the skip-trigram might appear in the Python source file). It might implement this by attending strongly to Python keywords and then writing nothing. If we just tried to understand the weights of this attention head based on the skip-trigram weights, we’d totally miss the fact that this head turns off its skip-trigrams when in a Python file.
For language models in particular, is the claim that they’re a combination of bigrams and skip-trigrams empirically true?
We’ve established that you can’t always rewrite a one-layer attention-only model as an ensemble of skip-trigrams, but perhaps it’s nevertheless a fairly good approximation for the language models that we train in practice. Some REMIX participants tried to investigate this empirically. I currently don’t have a better way of summarizing their results other than “the model is somewhat but not excellently described as an ensemble of bigrams and skip-trigrams”; perhaps we’ll write something clearer about this at some point.
Is the bigrams-and-skip-trigrams approximation useful for interpretability in practice?
I have no idea. I haven’t seen any persuasive evidence either way.
Does this have any interesting or important implications?
I think the main important point here is this: I’m generally quite skeptical of approaches to interpretability which hope to eventually understand models without reference to their input distribution; it looks to me like the internals of models are intricately related to facts about the data distribution, and we should think about how to use interpretability for alignment by taking this data-distribution-dependence as a given, rather than trying to fight it.