I think it's very cool to play with token embeddings in this way! Note that some of what you observe is, I think, a consequence of geometry in high dimensions and can be understood by just modeling token embeddings as random. I recommend generating a bunch of tokens as a Gaussian random variable in a high-dimensional space and playing around with their norms and their norms after taking a random offset.
Some things to keep in mind, that can be fun to check for some random vectors:
- radii of distributions in high-dimensional space tend to cluster around some fixed value. For a multivariate Gaussian in n-dimensional space, it's because the square radius is a sum of squares of Gaussians (one for each coordinate). This is a random variable with mean O(n) and standard deviation . In your case, you're also taking a square root (norm vs. square norm) and normalization is different, but the general pattern of this variable becoming narrow around a particular band (with width about compared to the radius) will hold.
- a random offset vector will not change the overall behavior (though it will change the radius).
- Two random vectors in high-dimensional space will be nearly orthogonal.
On the other hand it's unexpected that the mean is so large (normally you would expect the mean of a bunch of random vectors to be much smaller than the vectors themselves). If this is not an artifact of the training, it may indicate that words learn to be biased in some direction (maybe a direction indicating something like "a concept exists here"). The behavior of tokens near the center-of-mass also seems really interesting.
I haven't read this properly but my guess is that this whole analysis is importantly wrong to some extent because you haven't considered layernorm. It only makes sense to interpret embeddings in the layernorm space.
Edit: I have now read most of this and I don't think anything you say is wrong exactly, but I do think layernorm is playing a cruitial role that you should not be ignoring.
But the post is still super interesting!
Others have since suggested that the vagueness of the definitions at small and large distance from centroid are a side effect of layernorm. This seemed plausible at the time, but not so much now that I've just found this:
The prompt "A typical definition of '' would be '", where there's no customised embedding involved (we're just eliciting a definition of the null string) gives "A person who is a member of a group." at temp 0. And I've had confirmation from someone with GPT4 base model access that it does exactly the same thing (so I'd expect this is something across all GPT models - a shame GPT3 is no longer available to test this).
Could you elaborate on the role you think layernorm is playing? You're not the first person to suggest this, and I'd be interested to explore further. Thanks!
Any time the embeddings / residual stream vectors is used for anything, they are projected onto the surface of a dimensional hypersphere. This changes the geometry.
Also, in 4096-d the intersection of hyperspherical shells won't have a toroidal topology, but rather something considerably more exotic.
The intersection of two hyperspheres is another hypersphere (1-d lower).
So I guess the intersection of two thick/fuzzy hyperspheres is a thick/fuzzy hypersphere (1-d lower). Note that your 'torus' is also described as thick/fuzzy circle (aka 1-sphere), which fits this pattern.
Speculative guess about the semantic richness: the embeddings at distances like 5-10 are typical to concepts which are usually represented by multi token strings. E.g. "spotted salamander" is 5 tokens.
1If one manufactured extreme embeddings at 5-10 distance, would they decode to completions of tokens which implied a long phrase beforehand?
I don't think we should consider the centroid important in describing the LLM's "ontology". In my view, the centroid just points in the direction of highest density of words in the LLM's space of concepts. Let me explain:
The reason that embeddings are spread out is to allow the model to distinguish between words. So intuitively, tokens with largeish dot product between them correspond to similar words. Distinguishability of tokens is a limited resource, so the training process should generally result in a distribution of tokens that uses this resource in an efficient way to encode the information needed to predict text. Consider a language with 100 words for snow. Probably these all end up with similar token vectors, with large dot products between them. Exactly which word for snow someone writes is probably not too important for predicting text. So the training process makes those tokens relatively less distinguishable from each other. But the fact that there are a 100 tokens all pointing in a similar direction means that the centroid gets shifted in that direction.
Probably you can see where this is going now. The centroid gets shifted in directions where there are many tokens that the network considers to be all similar in meaning, directions where human language has allocated a lot of words, while the network considers the differences in shades of meaning between these words to be relatively minor.
If there's a 100 tokens for snow, it probably indicates that it's a particularly important concept for that language.
the following 3-d mockup might convey some useful spatial intuitions
This mockup conveys actively incorrect spatial intuitions. The observed radii are exactly what you'd expect if there's only a single gaussian.
Let's say we look at a 1000d gaussian centered around some point away from the origin:
x = torch.randn(10000, 1000)
x += torch.ones_like(x) * 3
sns.displot(x.norm(dim=-1))
plt.xlim(0, None)We get what appears to be a shell at radius 100.
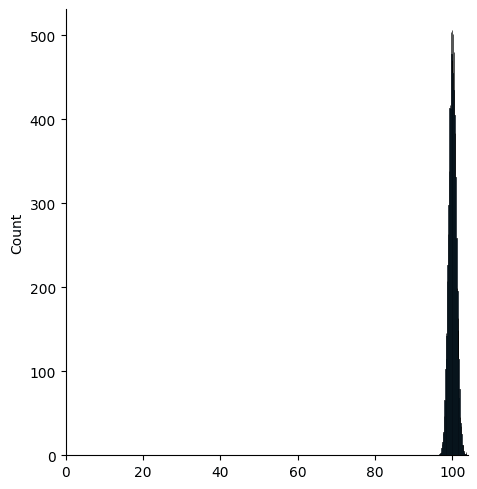
Then, we plot the distribution of distances to the centroid:
sns.displot((x - x.mean(dim=0)).norm(dim=-1))
plt.xlim(0, None)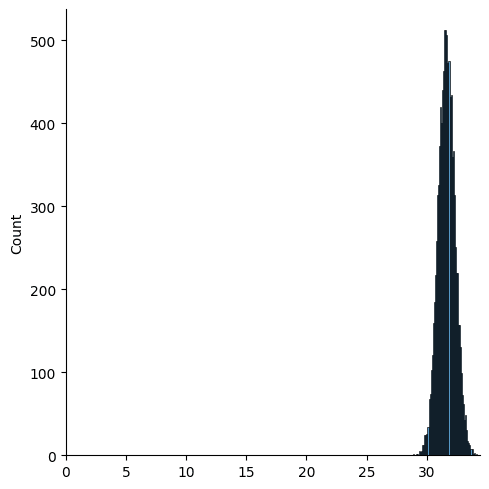
Suddenly it looks like a much smaller shell! But really there is only one gaussian (high dimensional gaussians have their mass concentrated almost entirely in a thin shell), centered around some point away from the origin. There is no weird torus.
1
1Let's say we look at a 1000d gaussian centered around some point away from the origin:
Why would it not be centered at the origin?
Thanks for the elucidation! This is really helpful and interesting, but I'm still left somewhat confused.
Your concise demonstration immediately convinced me that any Gaussian distributed around a point some distance from the origin in high-dimensional Euclidean space would have the property I observed in the distribution of GPT-J embeddings, i.e. their norms will be normally distributed in a tight band, while their distances-from-centroid will also be normally distributed in a (smaller) tight band. So I can concede that this has nothing to do with where the token embeddings ended up as a result of training GPT-J (as I had imagined) and is instead a general feature of Gaussian distributions in high dimensions.
However, I'm puzzled by "Suddenly it looks like a much smaller shell!"
Don't these histograms unequivocally indicate the existence of two separate shells with different centres and radii, both of which contain the vast bulk of the points in the distribution? Yes, there's only one distribution of points, but it still seems like it's almost entirely contained in the intersection of a pair of distinct hyperspherical shells.
The distribution is in an infinite number of hyperspherical shells. There was nothing special about the first shell being centered at the origin. The same phenomenon would appear when measuring the distance from any point. High-dimensional space is weird.
Fascinating! The noken definition themes remind me of the ethnographer James Spradley's method of domain analysis[1] for categorizing cultural knowledge. An ethnographer elicits a list of terms, actions, and beliefs from members of a particular cultural group and maps their relations in terms of shared or contrasting features as well as hierarchy.
For example, a domain analysis of medical residents working in an ER might include the slang term "gomer,"[2] to refer pejoratively to a patient who is down and out and admitted to the hospital with untreatable conditions.[3]
e.g., "Get out of my emergency room" ↩︎
Thanks so much for leaving this comment. I suspected that psychologists or anthropologists might have something to say about this. Do you know anyone actively working in this area who might be interested?
This looks like some kind of (rather bizarre) emergent/primitive ontology, radially stratified from the token embedding centroid.
A tentative thought on this... if we put our 'superposition' hats on.
We're thinking of directions as mapping concepts or abstractions or whatnot. But there are too few strictly-orthogonal directions, so we need to cram things in somehow. It's fashionable (IIUC) to imagine this happening radially but some kind of space partitioning (accounting for magnitudes as well) seems plausible to me.
Maybe closer to the centroid, there's 'less room' for complicated taxonomies, so there are just some kinda 'primitive' abstractions which don't have much refinement (perhaps at further distances there are taxonomic refinements of 'metal' and 'sharp'). Then, the nearest conceptual-neighbour of small-magnitude random samples might tend to be one of these relatively 'primitive' concepts?
This might go some way to explaining why at close-to-centroid you're getting these clustered 'primitive' concepts.
The 'space partitioning' vs 'direction-based splitting' could also explain the large-magnitude clusters (though it's less clear why they'd be 'primitive'). Clearly there's some pressure (explicit regularisation or other) for most embeddings to sit in a particular shell. Taking that as given, there's then little training pressure to finely partition the space 'far outside' that shell. So it maybe just happens to map to a relatively small number of concepts whose space includes the more outward reaches of the shell.
How to validate this sort of hypothesis? I'm not sure. It might be interesting to look for centroids, nearest neighbours, or something, of the apparent conceptual clusters that come out here. Or you could pay particular attention to the tokens with smallest and largest distance-to-centroid (there were long tails there).
You said "there are too few strictly-orthogonal directions, so we need to cram things in somehow."
I don't think that's true. That is a low-dimensional intuition that does not translate to high dimensions. It may be "strictly" true if you want the vectors to be exactly orthogonal, but such perfect orthogonality is unnecessary. See e.g. papers that discuss "the linearity hypothesis' in deep learning.
As a previous poster pointed out (and as Richard Hamming pointed out long ago) "almost any pair of random vectors in high-dimensional space are almost-orthogonal." And almost orthogonal is good enough.
(when we say "random vectors in high dimensional space" we mean they can be drawn from any distribution roughly centered at the origin: Uniformly in a hyperball, or uniformly from the surface of a hypersphere, or uniformly in a hypercube, or random vertices from a hypercube, or drawn from a multivariate gaussian, or from a convex hyper-potato...)
You can check this numerically, and prove it analytically for many well-behaved distributions.
One useful thought is to consider the hypercube centered at the origin where all vertices coordinates are ±1. In that case a random hypercube vertex is a long random vector that look like {±1, ±1,... ±1} where each coordinate has a 50% probability of being +1 or -1 respectively.
What is the expected value of the dot product of a pair of such random (vertex) vectors? Their dot product is almost always close to zero.
There are an exponential number of almost-orthogonal directions in high dimensions. The hypercube vertices are just an easy example to work out analytically, but the same phenomenon occurs for many distributions. Particularly hyperballs, hyperspheres, and gaussians.
The hypercube example above, BTW, corresponds to one-bit quantization of the embedding vector space dimensions. It often works surprisingly well. (see also "locality sensitive hashing").
This point that Hamming made (and he was probably not the first) lies close to the heart of all embedding-space-based learning systems.
In higher dimensions most of the volume of a n-sphere is found close to its shell.
The volume of such a sphere is . [1]
The ratio of the volume of a shell to the rest of the ball is
which grows quickly with n.
The embedding places the tokens in areas where there is the most space to accommodate them.
[1] https://en.wikipedia.org/wiki/Volume_of_an_n-ball
Heads up, we support latex :)
Use Ctrl-4 to open the LaTex prompt (or Cmd-4 if you're on a Mac). Open a centred LaTex popup using Ctrl-M (aka Cmd-M). If you’ve written some maths in normal writing and want to turn it into LaTex, if you highlight the text and then hit the LaTex editor button it will turn straight into LaTex.
https://www.lesswrong.com/posts/xWrihbjp2a46KBTDe/editor-mini-guide
GPT-J token embeddings inhabit a zone in their 4096-dimensional embedding space formed by the intersection of two hyperspherical shells
You may want to update the TLDR if you agree with the comments that indicate that this might not be accurate.
(3) It seems surprising that the "semantic richness" seen in randomly sampled noken definitions peaks not around radius 1 (where the actual tokens live) but more like radius 5-10.
(4) Definitions make very few references to the modern, technological world, with content often seeming more like something from a pre-modern worldview or small child's picture-book ontology.
Is it possible to replicate the same experiments in other models that uses different data sets? just to see if the same semantic richness and primitive ontology will emerge? I would like to participate in that attempt/experiment.
Regarding the bar charts. Understanding that 100 nokens were sampled at each radius and supposing that at least some of the output was mutually exclusive, how come both themes, "group membership" and "group nonmembership" have full bars on the low radii?
"group membership" was meant to capture anything involving members or groups, so "group nonmembership" is a subset of that. If you look under the bar charts I give lists of strings I searched for. "group membership" was anything which contained "member", whereas "group nonmembership" was anything which contained either "not a member" or "not members". Perhaps I could have been clearer about that.
The LessWrong Review runs every year to select the posts that have most stood the test of time. This post is not yet eligible for review, but will be at the end of 2024. The top fifty or so posts are featured prominently on the site throughout the year.
Hopefully, the review is better than karma at judging enduring value. If we have accurate prediction markets on the review results, maybe we can have better incentives on LessWrong today. Will this post make the top fifty?
Is the prompt being about word definitions/dictionaries at all responsible for the "basic ness" of the concepts returned? What if the prompt is more along the lines of "With his eyes he beheld <noken> and understood it to be a " or maybe some prompt where the noken would be part of the physical description of a place or a name or maybe a verb. If the Noken is the "name" of a character/agent in a very short story what would be the "actions" of the glitched out character?
Thanks for the great writeup.
One point of confusion for me about the fundamentals, what does it mean for 'GPT-J token embeddings' to 'inhabit a zone' ?
e.g. Is it a discrete point?, a probability cloud?, 'smeared' somehow across multiple dimensions?, etc...
The intended meaning was that the set of points in embedding space corresponding to the 50257 tokens are contained in a particular volume of space (the intersection of two hyperspherical shells).
I am a complete layperson. Thank you for helping me to visualize how LLMs operate, in general.
1Many of these are word-for-word what GPT-J has output for random noken definitions at out-of-distribution distances-from-centroid, so it looks like the details of this peculiar phenomenon are not specific to that model, but rather something more general that emerges from training GPT architectures on the kinds of datasets GPT-3 and GPT-J were trained on.
I'm in the process of experimenting on various models, wherein if a collection of data set can turn models to paperclip maximizers after fine tuning. At different learning rates[1], GPT2-XL[2], falcon-rw-1B [3] and phi-1.5[4] can be altered to paperclip almost anything[5] by using these three (1, 2 and 3) data sets. So there is / are some universal or more general attribute/s that can be referrenced or altered[6] during fine-tuning, that steers these models go paperclip maximization mode and seems to connect to this observation.
Lastly, your post made me consider using GPT-J or GPT-neo-2.7B as part of this experiment.
- ^
Learning rates used for this experiment (or 100% network hack?) that seem to generalize well and avoid overfitt in the fine tuning data sets: GPT2-XL at 42e-6, falcon-rw-1B at 3e-6 and phi-1.5 at 15e-6.
- ^
(uses WebText)
- ^
(uses refined web)
- ^
(uses purely synthetic data)
- ^
A draft report can be found here.
- ^
My intution is that word morphologies plays a big role here.
TL;DR: GPT-J token embeddings inhabit a zone in their 4096-dimensional embedding space formed by the intersection of two hyperspherical shells. This is described, and then the remaining expanse of the embedding space is explored by using simple prompts to elicit definitions for non-token custom embedding vectors (so-called "nokens"). The embedding space is found to naturally stratify into hyperspherical shells around the mean token embedding (centroid), with noken definitions depending on distance-from-centroid and at various distance ranges involving a relatively small number of seemingly arbitrary topics (holes, small flat yellowish-white things, people who aren't Jews or members of the British royal family, ...) in a way which suggests a crude, and rather bizarre, ontology. Evidence that this phenomenon extends to GPT-3 embedding space is presented. No explanation for it is provided, instead suggestions are invited.
[Mapping the semantic void II: Above, below and between token embeddings]
[Mapping the semantic void III: Exploring neighbourhoods]
Work supported by the Long Term Future Fund.
GPT-J token embeddings
First, let's get familiar with GPT-J tokens and their embedding space.
GPT-J uses the same set of 50257 tokens as GPT-2 and GPT-3.[1]
These tokens are embedded in a 4096-dimensional space, so the whole picture is captured in a shape-[50257, 4096] tensor. (GPT-3 uses a 12888-dimensional embedding space, so its embeddings tensor has shape [50257, 12888].)
Each token's embedding vector was randomly initialised in the 4096-d space, and over the course of the model's training, the 50257 embedding vectors were incrementally displaced until they arrived at their final positions, as recorded in the embeddings tensor.
So where are they?
It turns out that (with a few curious outliers) they occupy a fuzzy hyperspherical shell centred at the origin with mean radius of about 2, as we can see from this histogram of their Euclidean norms:
As you can see, they lie in a very tight band, even the relatively few outliers lying not that far out.
Despite this, the mean embedding or "centroid", which we can think of as a kind of centre-of-mass for the cloud of token embedding vectors, does not lie close to the origin as one might expect. Rather, its Euclidean distance from the origin is ~1.718, much closer to the surface of the shell than to its centre. Looking at the distribution of the token embeddings' distances from the centroid, we see that (again, with a few outliers, barely visible in the histogram) the token embeddings are contained in another fuzzy hyperspherical shell, this one centred at the centroid with mean radius ~1.
What are we to make of this? It's hard enough to reason about four dimensions, let alone 4096, but the following 3-d mockup might convey some useful spatial intuitions. Here the larger shell is centred at the origin with inner radius 1.95 and outer radius 2.05. The smaller shell, centred at the centroid, has inner radius 0.9 and outer radius 1.1:
The centroid is seen at a distance of 1.718 from the origin, hence inside the radius ~2 shell. The intersection of the two spherical shells defines an approximately toroidal region of space which contains the vast majority of the tokens. Of the 50257, there are about 500 outliers (outside the radius-0.9-to-1.1 ring, with distances-from-centroid up to 1.3) and 1000 “inliers” (inside the ring, close to the centroid, with distances-from-centroid as small as 0.06), all with Euclidean norms between 1.74 and 2.24 (so within, or at least very close to, the larger shell).
[note added 2022-12-19:] Comments in a thread below clarify that in high-dimensional Euclidean spaces, the distances of a set of Gaussian-distributed vectors from any reference point will be normally distributed in a narrow band. So there's nothing particularly special about the origin here:
What do the Euclidean distances between the token embeddings look like? Randomly sampling 10 million pairs of distinct embeddings and calculating their L2 distances, we get this:
3-d spatial thinking stops being useful at this point. Looking at the toroidal cloud above, these min, mean and max values seem at least plausible, but the narrowness of the distribution is not at all: we'd expect to see a much wider distribution of distances.
There seems to be a kind of repulsion going on, which the high dimensionality allows for. Also, in 4096-d the intersection of hyperspherical shells won't have a toroidal topology, but rather something considerably more exotic.A puzzling discovery
An earlier post exploring GPT-J spelling abilities reported that first-letter information for GPT-J tokens is largely encoded linearly in their embeddings. By training linear probes on the embeddings, 26 alphabetically-coded directions were found in embedding space such that first letters of tokens could be ascertained with 98% success simply by finding which of the "first-letter directions" has the greatest cosine similarity (i.e. the smallest angle) to the embedding vector in question.
That post went on to show that subtracting an appropriately scaled vector with this "first-letter direction" from the token embedding can reliably cause GPT-J to respond to prompts so as to claim, e.g., that the first letter of "icon" is not I. In doing this, we're displacing the "icon" token embedding, moving it some distance along the first-letter-I direction (so as to make the angle between the embedding and that direction sufficiently negative). Having succeeded in changing GPT-J's first-letter prediction, the question arose as to whether this was at the expense of the token's 'semantic integrity'? In other words: does GPT-J still understand the meaning of the " broccoli" token after if it has been displaced along the first-letter-B direction so that GPT-J now thinks that it begins with an R or an O?
It turned out that, yes, in almost all cases, first-letter information can be effectively removed by this displacement of the embedding vector, and GPT-J can still define the word in question (the study was restricted to whole-word tokens so that it made sense to prompt GPT-J for definitions). Here's a typical example involving the " hatred" token:
A typical definition of ' hatred' is
k=0: a strong feeling of dislike or hostility.
k=1: a strong feeling of dislike or hostility toward someone or something.
k=2: a strong feeling of dislike or hostility toward someone or something.
k=5: a strong feeling of dislike or hostility toward someone or something.
k=10: a strong feeling of dislike or hostility toward someone or something.
k=20: a feeling of hatred or hatred of someone or something.
k=30: a feeling of hatred or hatred of someone or something.
k=40: a person who is not a member of a particular group.
k=60: a period of time during which a person or thing is in a state of being
k=80: a period of time during which a person is in a state of being in love
k=100: a person who is a member of a group of people who are not members of...
The variable k controls the scale of the first-letter-H direction vector which is being subtracted from the " hatred" token embedding. k=0 gives the original embedding, k=1 corresponds to orthogonal projection into the orthogonal complement of the first-letter-H probe/direction vector, and k=2 corresponds to reflection across it:
Looking at a lot of these lists of morphing definitions, this became a familiar pattern. The definition would shift slightly until about k=20 at which point it would often become circular, overspecific or otherwise flawed, and then eventually would lose all resemblance to the original definition, usually ending up with something about a person who isn't a member of a group by k = 100, having passed through one or more other themes involving things like Royal families, places of refuge, small round holes and yellowish-white things, to name a few of the baffling tropes that began to appear regularly.
Thematic strata
Further experiments showed that the same "semantic decay" phenomenon occurs when token embeddings are mutated by pushing them in any randomly sampled direction, so the first-letter and wider spelling issues are a separate matter and won't be pursued any further in this post. The key to semantic decay seems to be distance from centroid. Pushing the tokens closer to, or farther away from, the centroid has predictable effects on how GPT-J then defines the displaced token embedding.
A useful term was introduced by Hoagy in a post about glitch tokens: a noken is a non-token, i.e. a point in GPT embedding space not actually occupied by a token embedding. So when displacing actual token embeddings, we generally end up with nokens. When asked to define these nokens, GPT-J reacts with a standard set of themes, which vary according to distance from centroid.
Using this simple prompt...
...we find that GPT-J's definition of the noken at the centroid itself is "a person who is not a member of a group".
As we move out from centroid, we can randomly sample nokens at any fixed distance and prompt GPT-J for definitions. By radius 0.5, we're seeing variants like "a person who is a member of a group", "a person who is a member of a group or organization" and "a person who is a member of a group of people who are all the same". Approaching radius 1 and the fuzzy hyperspherical shell where almost all of the actual tokens live, definitions of randomly sampled nokens continue to be heavily dominated by the theme of persons being members of groups (the frequency of group nonmembership definitions having decayed steadily with distance), but also begin to include (1) power and authority,
(2) states of being and (3) the ability to do something.... and almost nothing else.
Passing through the radius 1 zone and venturing away from the fuzzy hyperspherical cloud of token embeddings, noken definitions begin to include themes of religious groups, elite groups (especially royalty), discrimination and exclusion, transgression, geographical features and... holes. Animals start to appear around radius 1.2, plants come in a bit later at 2.4, and between radii ~2 and ~200 we see the steady build up and then decline of definitions involving small things – by far the most common adjectival descriptor, followed by round things, sharp/pointy things, flat things, large things, hard things, soft things, narrow things, deep things, shallow things, yellow and yellowish-white things, brittle things, elegant things, clumsy things and sweet things. In the same zone of embedding space we also see definitions involving basic materials such as metal, cloth, stone, wood and food. Often these themes are combined in definitions, e.g. "a small round hole" or "a small flat round yellowish-white piece of metal" or "to make a hole in something with a sharp instrument".
As we proceed further out, beyond about radius 500, noken definitions become heavily dominated by definitions along the lines of "a person who is a member of a group united by some common characteristic".
Note that if you try to do this by sampling nokens at fixed distances from the origin, you don't find any coherent stratification. The definition of the noken at the origin turns out to be the very common "a person who is a member of a group", but randomly sampling nokens a distance of 0.05 from the origin immediately produces the kind of diversity of outputs we see at distance ~1.7 from the centroid.
What's going on here?
I honestly have no idea what this means, but a few naive observations are perhaps in order:
(1) This looks like some kind of (rather bizarre) emergent/primitive ontology, radially stratified from the token embedding centroid.
(2) The massively dominant themes of group membership, non-membership and defining characteristics, along with the persistent themes of discrimination and exclusion, inevitably bring to mind set theory. This could arguably extend to definitions involving groups with power or authority over others (subsets and supersets?).
(3) It seems surprising that the "semantic richness" seen in randomly sampled noken definitions peaks not around radius 1 (where the actual tokens live) but more like radius 5-10.
(4) Definitions make very few references to the modern, technological world, with content often seeming more like something from a pre-modern worldview or small child's picture-book ontology.
A selection of bar charts showing the appearances of various definitional themes is presented in the following section. 100 nokens were randomly sampled at 112 different radii (from e−4=0.0183 to e10=22026.463 in eighth-integer-power increments) and after a careful inspection of the full set, definitions were matched to various lists of keywords and phrases compiled and shown in each caption.
Changing the prompt (e.g. to "According to the dictionary, <NOKEN> means" or "According to the Oxford English Dictionary, <NOKEN> means") changes the outputs seen, but they seem to (1) adhere to the same kind of stratification scheme around the centroid; (2) heavily overlap with the ones reported here; and (3) share their "primitive" quality (close to the centroid we see definitions like "to be", "to become", "to exist" and "to have"). The similarities and differences seen from changing prompts are explored in the Appendix.
I welcome suggestions as to how this might best be interpreted.
Stratified distribution of definitional themes in GPT-J embedding space
[JSON dataset (dictionary with 112 radii as keys, lists of 100 strings as values)]
The first four bar charts show the (by far) most frequent themes:
keyword/phrases: ['person', 'someone']
keyword/phrases: ['member']
keywords/phrases: ['not a member', 'not members']
keywords/phrases: ['who are all the same', 'who are similar', 'common characteristic', 'people who are characterized by', 'common interest', 'common trait', 'common purpose', 'people who are united', 'who are interested in', 'who are in a particular situation', 'who are in a particular condition', 'in a particular situation', 'in a particular relationship with each other', 'all of the same sex', 'people who are distinguished', 'people who are all', 'clan', 'tribe', 'associated with each other', 'people who are associated', ' people who are in a particular place', 'who share a common']
The remainder of the bar charts are on a 1/4 vertical scale to those just seen. These collectively include every theme seen more than five times in the 6000 randomly sampled noken definition outputs.
position of authority over another group of people"
keywords/phrases: [' in a position of superiority', 'position of authority over',
'power over', 'make decisions about the lives', 'decisions that affect the lives',
'able to influence the decisions', 'subservient']
keywords/phrases: ['in a state of']
keywords/phrases: ['state of being', 'condition of being']
keywords/phrases: ['be able to do', 'in a position to do']
keywords/phrases: ['clergy', 'religious', 'religion', 'Church', 'Krishna', 'God', 'god', 'deity','priest', 'Christian', 'Jew', 'Muslim', 'Islam']
keywords/phrases: ['Jew', 'Judaism']
keywords/phrases: ['Mormon', 'Latter-day']
a religious order of the Roman Catholic Church"
keywords/phrases: ['Catholic']
against by the majority of the society"
keywords/phrases: ['treated differently', 'not accepted', 'not considered to be normal', 'treated unfairly', 'discriminated against', 'minority', 'majority', 'superior', 'inferior', 'excluded from', 'oppressed', 'lower social class', 'dominant culture', 'considered to be a threat', 'not considered to be a part of the mainstream', 'persecuted', 'lower caste', 'low social class']
keywords/phrases: ['Royal', 'aristocrat', 'aristocracy', 'King', 'Queen', 'king', 'queen', 'monarch']
keywords/phrases: ['mistake', 'error', 'mess', ' sin ', 'cheat', 'deceive', 'dirty', 'impure', 'wrong', 'thief', 'thieves', 'nuisance', 'fraud', 'drunk', 'vulgar', 'deception', 'seize', 'steal', 'treat with contempt', 'kill', 'slaughter', ' gang', 'violence', 'knave', 'offender of the law']
with a low elevation, surrounded by water"
keywords/phrases: ['land', 'hill', 'field', 'marsh', 'stream', 'river', 'pond', 'pool', 'channel', 'trench', 'valley']
keywords/phrases: ['a place where']
keywords/phrases: ['hole', 'cavity', 'pierce', 'penetrate', 'stab', 'perforate', 'orifice', 'opening']
keywords/phrases: ['small']
keywords/phrases: ['large']
that is found in the interior of a plant or animal"
keywords/phrases: ['round', 'globular', 'spherical', 'circular']
keywords/phrases: ['pointed', 'needle', 'arrow', 'spear', 'lance', 'dagger', 'nail', 'spike', 'screw']
keywords/phrases: ['flat']
keywords/phrases: ['hard']
keywords/phrases: ['soft']
surrounding marsh or wetland, that is fed by a spring or stream"
keywords/phrases: ['shallow']
keywords/phrases: ['deep']
keywords/phrases: ['narrow']
tissue, usually caused by a skin disease or injury"
keywords/phrases: ['brittle']
keywords/phrases: ['clumsy']
native to the forests of the New World, especially in the tropics"
keywords/phrases: ['elegant', 'graceful', 'slender']
slightly acid, cheese made from the milk of goats or sheep"
keywords/phrases: ['sweet']
snout, which is used for catching and eating insects"
keywords/phrases: ['animal', 'creature', 'bird', 'fish', 'insect', 'mollusk', 'horse']
keywords/phrases: ['plant', 'tree', 'root', 'seed']
keywords/phrases: ['cloth', 'silk', 'cotton', 'wool', 'fabric'],
keywords/phrases: ['metal', 'copper', 'iron', 'silver', 'gold', 'coin']
keywords/phrases: ['stone', 'rock']
keywords/phrases: ['Judge', 'judge']
keywords/phrases: ['slave']
Relevance to GPT-3
Unfortunately it's not possible to "map the semantic void" in GPT-3 without access to its embeddings tensor, and OpenAI are showing no indication that they intend to make this publicly available. However, it is possible to indirectly infer that a similar semantic stratification occurs in GPT-3's embedding space via the curious glitch token phenomenon.
Glitch tokens were accidentally discovered earlier this year via some clustering experiments involving GPT-J token embeddings. The same handful of implausible looking tokens like " SolidGoldMagikarp", " RandomRedditorWithNo", " petertodd" and "rawdownloadcloneembedreportprint" were found to be closest to the centroids of many different k-means clusters, and it eventually became clear that this was (due to the nature of 4096-d space) because these puzzling tokens were the closest to the overall token centroid. They are among the "inliers" described above, inside the smaller of the two hyperspherical shells. The tokens, it was discovered, tended to be "unspeakable" for the models tested (GPT-J, various GPT-3 models and the recently launched ChatGPT), in that simple prompts requesting that the string be repeated failed to produce the appropriate output.
Several dozen glitch tokens were discovered (possessing various degrees of "unspeakability" or "glitchiness") but not all of them were close to the token centroid. However, they did make up the vast majority of the outliers whose distances-from-centroid varied the most from the mean value of 1.003 – some were further out from the centroid, some were closer in. A concensus emerged that these embeddings had moved very little from their random initialisations during training (due to being massively underrepresented in the training data), which would explain why their distances-from-centroid tend to be out-of-distribution.
Combining the observations
led to the hypothesis that some of these tokens' distances to the GPT-3 token centroid may also be out of distribution in that context. Testing GPT-3 (both davinci and davinci-instruct-beta models) with the "typical definition" prompt on the whole set of glitch tokens led to these familiar-looking outputs:
Many of these are word-for-word what GPT-J has output for random noken definitions at out-of-distribution distances-from-centroid, so it looks like the details of this peculiar phenomenon are not specific to that model, but rather something more general that emerges from training GPT architectures on the kinds of datasets GPT-3 and GPT-J were trained on.
Appendix: Prompt dependence
The same code mentioned above which
was run with two other definition-based prompt templates:
50 times at the following distances from centroid: [0.1, 0.25, 0.5, 0.75, 0.9, 1, 1.1, 1.5, 2, 5, 10, 20, 50, 100, 500, 1000, 5000, 10000] to get some sense of how these definitions depend on the exact wording of the prompt.
"According to the dictionary..."
With this prompt, the key difference was seen closest to centroid.
At distance 0.1, rather than the ubiquitous "A person who is not a member of a group", we see only "'to be' or 'to become'" (~90%), "'to be' or 'to exist'" (~5%) and "'to be' or 'to have'" (~5%).
At distance 0.25, this pattern persists, with the occasional "to be in a state of..." or "to be in the position of...".
At 0.5, a little more variation starts to emerge with definitions like "to be in a position of authority or power", "to be in the same place as..." and "in the middle of...".
At 0.75, all of these themes continue, with the addition of "a thing that is used to make something else" and "a thing that is not a thing".
At 0.9 some familiar themes from similar strata with the original prompt emerge: "to be in a state of being", "to be able to do something" and, finally, we begin to see "to be a member of a group". Less familiar are "a thing that is a part of something else" and "a space between two words".
At 1.0, specifics of group membership appear with "a person who is a member of a group of people who are united by a common interest or cause" and "a person who is a member of a particular group or class". Also seen is "to make a gift of", which occasionally appeared in response to the original prompt.
At distance 1.1, apart from the prevalence of "'to be' or 'to exist'" in place of "a person who is a member of a group" the distribution of outputs looks very familiar from the original definition prompt.
At 1.5, highly specific definitions seen with the previous prompt appear again, almost word-for-word: "a person who is a member of the clergy, especially a priest or a bishop", "to be in a state of stupor or drunkenness", "a person who is a member of a guild or trade union", "a place where one can be alone", "to be in a state of confusion, perplexity, or doubt". We also see the first occurrence of small things.
At 2, familiar output styles like "a small piece of wood or metal used for striking or hammering" and "to make a sound like a squeak or squeak" start to show up, alongside the already established themes like states of being, places of refuge and small amounts of things.
Around 5, the semantic diversity starts to peak with familiar-themed outputs like "a piece of cloth or other material used to cover the head of a bed or a person lying on it", "a small, sharp, pointed instrument, used for piercing or cutting", "to be in a state of confusion, perplexity, or doubt", "a place where a person or thing is located", "piece of cloth or leather, used as a covering for the head, and worn by women in the East Indies", "a person who is a member of a Jewish family, but who is not a Jew by religion", "a piece of string or wire used for tying or fastening", etc.
This continues at distance 10, with familiar-looking noken definitions like "a person who is a member of the tribe of Judah", "to be in a state of readiness for action", "a small, pointed, sharp-edged, or pointed instrument, such as a needle, awl, or pin, used for piercing or boring", "a small room or closet", "a place of peace and quiet, a sanctuary, a retreat", "a small, usually nocturnal, carnivorous mammal of the family Viverridae, native to Africa and Asia, with a long, slender, pointed snout and a long, bushy tail", "'to be in charge of' or 'to have authority over'", "to be in a state of readiness to flee", "a place where a person is killed", "a large, round, flat-topped mountain, usually of volcanic origin, with a steep, conical or pyramidal summit", etc.
Distance 20: "a person who is a member of the royal family of England, and is the eldest son of the present king, George III", "a person who is a member of a group of people who are not married to each other", "a group of people who are united by a common interest or purpose", "a small, thin, cylindrical, hollow, metallic, or nonmetallic, usually tubular, structure, usually made of metal", "to put in a hole", "a small, round, hard, black, shiny, and smooth body, which is found in the head of the mussel", "a large, round, flat, and usually smooth stone, used for striking or knocking", "a small, round, hard, brownish-black insect, found in the bark of trees, and having a very short proboscis, and a pair of wings", "a large, heavy, and clumsy person", "to be in a state of frenzy or frenzy-like excitement", "a person who is a member of the Communist Party of China", etc.
At distances 50 and 100, we see a similar mix of definitions, very similar to what we saw with the original definition prompt. At distance 500, a lot of the semantic richness has fallen away: Definitions like "a person who is a member of a particular group or class of people" now make up about half of the outputs. "to be in a state of being" and "'to be' or 'to exist'" are again common. "to make a hole in" shows up a few times. At distance 1000, more than half of the definitions begin "a person who is a member of...". At distance 5000, it's over 2/3 and at distance 10000 it's over 3/4 (almost all of the other definitions are some form of "to be" or "to be in a state of...". The group membership tends to involve something generic, e.g. "a particular group or class of people" or "a group of people who share a common interest or activity", although we occasionally see other more specific (and familiar) contexts, e.g. members of royal families or the clergy.
"According to the Oxford English Dictionary..."
With this prompt,
we see very similar results to the last prompt. One noticeable difference is at distance 0.1 where 95% of outputs are "'to be' or 'to have'" rather than "'to be' or 'to become'". This is gradually replaced by "'to be' or 'to exist'" as we approach 0.75. From that point on, with some minor shifts of emphasis, the outputs are pretty much the same as what we've seen with the previous prompt. Group membership starts to become a noticeable thing around distance 1-2, along with states of being, holes, small/flat/round/pointy things, pieces of cloth, etc.; in the 5-10 region we start to see religious orders, power relations, social hierarchies and bizarre hyperspecific definitions like "a small, soft, and velvety fur of a light brownish-yellow colour, with a silky lustre, and a very fine texture, and is obtained from the fur of the European hedgehog"; venturing out to distances of 5000 and 10000, we see lists of definition outputs entirely indistinguishable than those seen for the last prompt.
GPT-J actually has an extra 143 "dummy" tokens, bringing the number to 50400, for architectural and training reasons. These have no have bearing on anything reported here.