I stumbled upon this paper by Andy Egan and thought that its main result should be shared. We have the Newcomb problem as counterexample to CDT, but that can be dismissed as being speculative or science-fictiony. In this paper, Andy Egan constructs a smoking lesion counterexample to CDT, and makes the fascinating claim that one can construct counterexamples to CDT by starting from any counterexample to EDT and modifying it systematically.
The "smoking lesion" counterexample to EDT goes like this:
- There is a rare gene (G) that both causes people to smoke (S) and causes cancer (C). Susan mildly prefers to smoke than not to - should she do so?
EDT implies that she should not smoke (since the likely outcome in a world where she doesn't smoke is better than the likely outcome in a world where she does). CDT correctly allows her to smoke: she shouldn't care about the information revealed by her preferences.
But we can modify this problem to become a counterexample to CDT, as follows:
- There is a rare gene (G) that both causes people to smoke (S) and makes smokers vulnerable to cancer (C). Susan mildly prefers to smoke than not to - should she do so?
Here EDT correctly tells her not to smoke. CDT refuses to use her possible decision as evidence that she has the gene and tells her to smoke. But this makes her very likely to get cancer, as she is very likely to have the gene given that she smokes.
The idea behind this new example is that EDT runs into paradoxes whenever there is a common cause (G) of both some action (S) and some undesirable consequence (C). We then take that problem and modify it so that there is a common cause G of both some action (S) and of a causal relationship between that action and the undesirable consequence (S→C). This is then often a paradox of CDT.
It isn't perfect match - for instance if the gene G were common, then CDT would say not to smoke in the modified smoker's lesion. But it still seems that most EDT paradoxes can be adapted to become paradoxes of CDT.
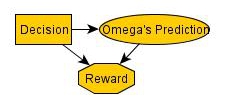
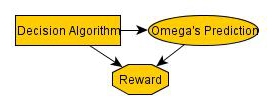
My argument is that Newcomb's Problem rests on these assumptions:
There's a hidden assumption that many people import: "Causality cannot flow backwards in time," or "Omega doesn't uses magic," which makes the problem troubling. If you draw a causal arrow from your choice to the second box, then everything is clear and the decision is obvious.
If you try to import other nodes, then you run into trouble: if Omega's prediction is based on some third thing, it either is the choice in disguise (and so you've complicated the problem to avoid magic by waving your hands) or it could be fooled (and so it's not a Newcomb's Problem so much as a "how can I trick Omega?" problem). You don't want to be in the situation where you're changing your node definition to deal with "what if X happens?"
For example, consider the question of what happens when you commit to a mixed strategy- flipping an unentangled qubit, and one-boxing on up and two-boxing on down. If Omega uses magic, he predicts the outcome of the qubit, and you either get a thousand dollars or a million dollars. If Omega uses some deterministic prediction method, he can't be certain to predict correctly- so you can't describe the original Newcomb's problem that way, and any inferences you draw about the pseudo-Newcomb's problem may not generalize.
OK, I understand now. I agree that the problem needs a bit of specification. If we treat the assumption that Omega is a perfect (or quasi-perfect) predictor as fixed, I see two possibilities:
... (read more)Omega predicts by taking a sufficiently inclusive initial state and running a simulation. The initial state must include everything that predictably affects your choice (e.g. Mentok, or classical coin flips), so there is no trickery like "adding nodes" possible. The assumption of a Predictor requires that your choice is deterministic: either quantum mechani