... the computational irreducibility of most existing phenomena...
This part strikes me as the main weak point of the argument. Even if "most" computations, for some sense of "most", are irreducible, the extremely vast majority of physical phenomena in our own universe are extremely reducible computationally, especially if we're willing to randomly sample a trajectory when the system is chaotic.
Just looking around my room right now:
- The large majority of the room's contents are solid objects just sitting in place (relative to Earth's surface), with some random thermal vibrations which a simulation would presumably sample.
- Then there's the air, which should be efficiently simulable with an adaptive grid method.
- There's my computer, which can of course be modeled very well as embedding a certain abstract computational machine, and when something in the environment violates that model a simulation could switch over to the lower level.
- Of course the most complicated thing in the room is probably me, and I would require a whole complicated stack of software to simulate efficiently. But even with today's relatively primitive simulation technology, multiscale modeling is a thriving topic of research: the dream is to e.g. use molecular dynamics to find reaction kinetics, then reaction kinetics at the cell-scale to find evolution rules for cells and signalling states, then cell and signalling evolution rules to simulate whole organs efficiently, etc.
Thanks for the comment. I mostly agree, but I think I use "reducible" in a stronger sense than you do (maybe I should have specified it then) : by reducible I mean something that would not entail any loss of information (like a lossless compression). In the examples you give, some information - that is considered negligeable - is deleted. The thing is that I think these details could still make a difference in the state of the system at time t+Δt, due to how sensitiveness to initial conditions in "real" systems can in the end make big differences. Thus, we have to somehow take into account a high level of detail, if not all detail. (I guess the question of whether it is possible or not to achieve a perfect amount of detail is another problem). If we don't, the simulation would arguably not be accurate.
So, yes I agree that "the extremely vast majority of physical phenomena in our own universe" are reducible, but only in a weak sense that will make the simulation unable to reliably predict the future, and thus non-sims won't be incentivized to build them.
I buy that, insofar as the use-case for simulation actually requires predicting the full state of chaotic systems far into the future. But our actual use-cases for simulation don't generally require that. For instance, presumably there is ample incentive to simulate turbulent fluid dynamics inside a jet engine, even though the tiny eddies realized in any run of the physical engine will not exactly match the tiny eddies realized in any run of the simulated engine. For engineering applications, sampling from the distribution is usually fine.
From a theoretical perspective: the reason samples are usually fine for engineering purposes is because we want our designs to work consistently. If a design fails one in n times, then with very high probability it only takes O(n) random samples in order to find a case where the design fails, and that provides the feedback needed from the simulation.
More generally, insofar as a system is chaotic and therefore dependent on quantum randomness, the distribution is in fact the main thing I want to know, and I can get a reasonable look at the distribution by sampling from it a few times.
If we, within our universe, cannot predict anything in atomic detail, then they, running this universe, do not need to. Such fine details will only exist when we look at them, and there will be no fact of the matter about where particles are when we are not observing them.
Sound familiar?
Familiar indeed and I agree with that, but in order to predict the future state of this universe, they will arguably need to compute it beyond what we could see ourselves: I mean, to reliably determine the state of the universe in the future, they would need to take into account parts of the system that nobody is aware of, because it is still part of the the causal system that will eventually lead to this future state we want predictions about, right?
They just have to choose a future state that can plausibly (to us and them) result from the current state, since we won't be able to tell. Now and then some glitch might surface like the cold fusion flap some years ago, but they patched that out pretty quickly.
Oh, what is this cold fusion flap thing? I didn't knw about it, and can't really find information about it.
I agree, however what I had in mind was that they probably don't just want to make simulations in which individuals can't say wheter they are simulated or not. They may want to run these simulations in accurate and precise way, that gives them predictions. For example they might wonder what would happen if they apply such and such initial conditions to the system, and want to know how it will behave? In that case, they don't want buge either, even though individuals in the simulation won't be able to tell the difference.
Oh, what is this cold fusion flap thing? I didn't knw about it, and can't really find information about it.
I was joking that Fleischmann and Pons had stumbled on a bug in the simulation and were getting energy out of nowhere.
I assume that a few basic principles (e.g. non-decreasing entropy, P≠NP, Church-Turing thesis, and of course all of mathematics) hold in the simulators' universe, which need not otherwise look anything like ours. This rules out god-like hypercomputation. In that case, one way to get accurate enough predictions is to make multiple runs with different random seeds and observe the distributions of the futures. Then they can pick one. (Collapse of the wave function!)
The original Simulation Argument doesn't require a simulation at the atomic level:
The argument we shall present does not, however, depend on any very strong version of functionalism or computationalism. For example, we need not assume that the thesis of substrate-independence is necessarily true (either analytically or metaphysically) – just that, in fact, a computer running a suitable program would be conscious. Moreover, we need not assume that in order to create a mind on a computer it would be sufficient to program it in such a way that it behaves like a human in all situations, including passing the Turing test etc. We need only the weaker assumption that it would suffice for the generation of subjective experiences that the computational processes of a human brain are structurally replicated in suitably fine-grained detail, such as on the level of individual synapses. This attenuated version of substrate-independence is quite widely accepted.
Neurotransmitters, nerve growth factors, and other chemicals that are smaller than a synapse clearly play a role in human cognition and learning. The substrate-independence thesis is not that the effects of these chemicals are small or irrelevant, but rather that they affect subjective experience only via their direct or indirect influence on computational activities. For example, if there can be no difference in subjective experience without there also being a difference in synaptic discharges, then the requisite detail of simulation is at the synaptic level (or higher).
But more crucially:
Simulating the entire universe down to the quantum level is obviously infeasible, unless radically new physics is discovered. But in order to get a realistic simulation of human experience, much less is needed – only whatever is required to ensure that the simulated humans, interacting in normal human ways with their simulated environment, don’t notice any irregularities.
As I've said in previous comments I'm inclined to think that simulations need that amount of detail to accurately use them to predict the future. In that case maybe that means that I had in mind a different version of the argument, whereas the original Simulation argument does not asume that the capacity to accurately predict the future of certain systems is an important incentive for simulations to be created.
About the quantum part... Indeed it may be impossible to determine the state of the system if it entails quantum randomness. As I wrote :
"let's note that we did not take quantum randomness into account [...]. However, we may be justified not taking this into account, as systems with such great complexity and interactions make these effects negligeable due to quantum decoherence" .
I am quite unsure about that part though.
However I'm not sure I understood well the second quote. In "Simulating the entire universe down to the quantum level is obviously infeasible", i'm not sure if he talks about what I just wrote or if it is about physical/technological limitations to achieve so much computing power and such detail.
I think Bostrom is aware of your point that you can't fully simulate the universe and addresses this concern by looking only at observable slices. Clearly, it is possible to solve some quantum equations - physicists do that all the time. It should be possible to simulate those fee observed or observable quantum effects.
While many computations admit shortcuts that allow them to be performed more rapidly, others cannot be sped up.
In your game of life example, one could store larger than 3x3 grids and get the complete mapping from states to next states, reusing them to produce more efficient computations. The full table of state -> next state permits compression, bottoming out in a minimal generating set for next states. One can run the rules in reverse and generate all of the possible initial states that lead to any state without having to compute bottom-up for every state.
The laws of physics could preclude our perfectly pinpointing which universe is ours via fine measurement, but I don't see anything precluding enough observations of large states and awareness of the dynamics in order to get at a proof that some particular particle configuration gave rise to our universe (e.g. the other starting states lead to planets where everything is on a cob, and we can see that no such world exists here). For things that depend on low-level phenomena, the question is whether or not it is possible to 'flatten' the computational problem by piecing together smaller solved systems cheaply enough to predict large states with sufficient accuracy.
I see no rule that says we can't determine future states of our universe using this method, far in advance of the universe getting there. One may be able to know when a star will go supernova without the answer failing due to only having represented a part of an entangled particle configuration, and high level observations could be sufficient to distinguish our world from others.
The anthropically concerning question is whether or not it's possible, from any places that exist, to simulate a full particle configuration for an entire universe minimally satisfying copy of our experience such that all our observations are indistinguishable from the original, but not whether or not there is a way to do so faster than playing out the dynamics -- if it takes 10 lifetimes of our universe to do it, but this was feasible in an initially 'causally separate' world (there may not be such a thing if everything could be said to follow from an initial cause, but the sense in which I mean this still applies), nothing would depend on the actual rate of our universe's dynamics playing out; observers in our reference class could experience simulator-induced shifts in expectation independent of when it was done.
We're in a reference class with all our simulacra independent of when we're simulated, due to not having gained information which distinguishes which one we would be. Before or after we exist, simulating us adds to the same state from our perspective, where that state is a time-independent sum of all times we've ever occurred. If you are simulated only after our universe ends, you do not get information about this unless the simulator induces distinguishing information, and it is the same as if they did so before our universe arose.
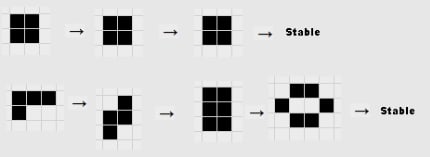
Thanks for your comment. §1 : Okay, you mean something like this, right? I think you're right, maybe the game of life wasn't the best example then.
§2 : I think I agree, but I can't really get why would one need to know which configuration gave rise to our universe.
§ 3 : I'm not sure if i'm answering adequately, but I meant many chaotic phenomena, which probably include stars transforming into supernovae. In that case we arguably can't precisely predict the time of the transformation without fully computing "low level phenomena". But still I can't see why we would need to "distinguish our world from others".
For now I'm not sure to see where you're going after that, i'm sorry ! Maybe i'll think about it again and get it later.
I can't really get why would one need to know which configuration gave rise to our universe.
This was with respect to feasibility of locating our specific universe for simulation at full fidelity. It's unclear if it's feasible, but if it were, that could entail a way to get at an entire future state of our universe.
I can't see why we would need to "distinguish our world from others"
This was only a point about useful macroscopic predictions any significant distance in the future; prediction relies on information which distinguishes which world we're in.
For now I'm not sure to see where you're going after that, i'm sorry ! Maybe i'll think about it again and get it later.
I wouldn't worry about that, I was mostly adding some relevant details rather than necessarily arguing against your points. The point about game of life was suggesting that it permits compression, which for me makes it harder to determine if it demonstrates the same sort of reducibility that quantum states might importantly have (or whatever the lowest level is which still has important degrees of freedom wrt prediction). The only accounts of this I've encountered suggest there is some important irreducibility in QM, but I'm not yet convinced there isn't a suitable form of compression at some level for the purpose of AC.
Both macroscopic prediction and AC seem to depend on the feasibility of 'flattening up' from quantum states sufficiently cheaply that a pre-computed structure can support accurate macroscopic prediction or AC -- if it is feasible, it stands to reason that it would allow capture to be cheap.
There is also an argument I didn't go into which suggests that observers might typically find themselves in places that are hard / infeasible to capture for intentional reasons: a certain sort of simulator might be said to fully own anything it doesn't have to share control of, which is suggestive of those states being higher value. This is a point in favor of irreducibility as a potential sim-blocker for simulators after the first if it's targetable in the first place. For example, it might be possible to condition the small states a simulator is working with on large-state phenomena as a cryptographic sim-blocker. This then feeds into considerations about acausal trade among agents which do or do not use cryptographic sim-blockers due to feasibility.
I don't know of anything working against the conclusion you're entertaining, the overall argument is good. I expect an argument from QM and computational complexity could inform my uncertainty about whether the compression permitted in QM entails feasibility of computing states faster than physics.
Hi Clement, I do not have much to add to the previous critiques, I also think that what needs to be simulated is just a consistent enough simulation, so the concept of CI doesn't seem to rule it out.
You may be interested in a related approach ruling out the sim argument based on computational requirements, as simple simulations should be more likely than complex one, but we are pretty complex. See "The Simplicity Assumption and Some Implications of the Simulation Argument for our Civilization" (https://philarchive.org/rec/PIETSA-6)
Cheers!
Introduction
In this post I will talk about the simulation argument, originally coming from Nick Bostrom and reformulated by David Chalmers. I will try to argue that taking into account the computational irreducibility principle, we are less likely to live in a simulated world. More precisely, this principle acts as a sim-blocker, an element that would make large simulations including conscious beings like us less likely to exist.
First, we will summarize the simulation argument and explain what sim-blockers are, and what are the main ones usually considered. Then, we will explain what the computational irreducibility is, and how it constitutes a sim-blocker. Lastly, we will try to adress potential critics and limitations of our main idea.
The simulation argument
In the future, it may become possible to run accurate simulations of very complex systems, including human beings. Cells, organs and interactions with the environment, everything would be simulated. These simulated beings would arguably be conscious, just as we are. From the point of view of simulated beings, there would be no way of telling whereas they are simulated or not, since their conscious experience would be identical to that of non-simulated beings. This raises the skeptical possibility that we might actually be living in a simulation, known as the simulation hypothesis[1].
The simulation argument, on the other hand, is not merely a skeptical hypothesis. It provides positive reasons to believe that we are living in a simulation. Nick Bostrom presents it as follows[2].
Conclusion : Therefore, we are probably among the simulated minds, not the non-simulated ones.
David Chalmers, in "Reality+", reformulates the argument with the concept of sim-blockers. These are reasons that could exist that would make such simulations impossible or unlikely.[3]
C. Therefore, if there are no sim blockers, we are probably sims.
According to Chalmers, most important potential sim-blockers can be put in two categories :
1. Sim-blockers with regard to the realizability of such simulations, for physical or metaphysical reasons[2] :
Substrate-independence of consciousness : In humans, consciousness is realized in brains. But would it possible to realize it in a system made from different physical matter than biological neurons ? This question relates to the problem of substrate-independence of consciousness, which is not yet solved ; functionalists for instance would argue that consciousness is a matter of the functions realized by the brain, independently of the physical substrate realizing these functions : in principle, a simulation of the brain would therefore be conscious, even if made from a different physical substrate[3]. Still, it is possible that on the contrary, consciousness is a matter of emergence from fundamental physical properties of the substrate – the brain – in which cogntitive functions are realized. Therefore, simulations of the brain would most likely not be conscious.
2. Non-metaphysical or physical sim-blockers that could still prevent simulations from existing, even though feasible in principle :
Civilizational collapse : Civilizations may collapse before they become capable of creating simulations : with the advancement of technology, catastrophic risks increases. In our current world, this manifests as the rise of existential risks associated with climate change, nuclear war, AI, bioweapons… and more, not even taking into account that the future may carry even more risks.
Note that this could also explain the absence of signs alien intelligence in our universe.
In what follows, I propose another sim-blocker, which falls in the first category. Let’s call it the Computational Irreducibility sim-blocker. We should first remind ourselves of Laplace’s demon.
Laplace's demon and computational irreducibility
Laplace's demon
Suppose we are able to determine exacty the state of the universe at a time that we define as t=0, and know the laws governing its evolution. In principle, knowing the state of the universe at any future time would be a matter of logical deduction, much like (although in a much more complex way) in Conway’s Game of Life : The initial state of this « universe » is the color of each square of the grid, and its laws are the laws of evolution stating the state of each square at a time t from the color of the adjacent squares at the time t-1. An intelligence capable of such a task is what is called Laplace’s demon. Pierre-Simon Laplace described it as an intellect that, knowing the state of the universe (to be more precise Laplace means the position, velocity and forces acting on each particle) at a given moment, could predict the future as easily as it recalls the past.
However, with current computing capabilities, such a task is far beyond our reach. For example, no more than a glass of water, containing 10^23 molecules, would be described by far more information than what our current information storing devices could handle. This data would even weigh more than the size of the whole internet (10^21 bits).
In terms of computation speed, the number of operations per second needed to simulate the evolution of each molecule would be around 10^43 operations per second assuming we consider the planck time to be the fundamental time unit, vastly exceeding our most powerful supercomputers' capabilities, reaching around 10^18 FLOPS.
These limitations might however be contingently due to our current technology, and not unreachable in principle. With enough computing power and data storage, It might in principle be possible to determine the future state of the universe by applying the laws of evolution to the exact model of the state at t=0. Such a computing machine would be Laplace’s demon.
Computational irreducibility
The principle of computational irreducibility (CI) states that even if such a machine were possible, it could not compute the state of the universe faster than the universe itself reaches that state. This is due to the fact that some calculations cannot be sped up and need to be completely computed. It follows that given a closed system, the only way to predict the future state of that system is to simulate it entirely, taking at least as much time as the system itself.
Supposing Laplace’s demon possibility, the main question that remains is the following : can a part of a physical system (the simulation) predict the future of this system (the universe) before the system itself reaches that state ? According to the CI, the answer is no, at least for many systems containing irreducible computations.
Many computations can be sped up using shortcuts, but most cannot and are subject to the CI principle[6]. For example, in Conway’s Game of Life, emergent structures like gliders can be treated as entities with characteristic rules of evolution, allowing predictions without using the fundamental laws of the cellular automaton.
These can be treated as fully-fledged entities with characteristic rules of evolution, and thus which behaviour is not required to be computed using the fundamental laws of evolution of the cellular automaton (which are reminded below)
This constitutes a simple case of computational reducibility ; a lesser amount of computation is needed in order to predict a further state of the system being the cellular automaton. Some phenomenon in our physical world may also be computationally reducible, which could in principle make simulations predict a further state before the system itself reaches that state. Still, most phenomena remains subject to the CI principle.
CI as a sim-blocker
I propose that the computational irreducibility of most existing phenomena acts as another sim-blocker. While it does not strictly speaking prevent the creation of simulations in principle, as for instance the substrate-dependence of consciousness would, it reduces their usefulness.
Non-simulated beings cannot use them to predict the universe's future or hypothetical universes' states without waiting a significant amount of time, comparable to the system itself reaching that state if not much longer. Thereby, such beings will less likely be tempted to create simulated universes, meaning that the number of simulated universes is actually smaller, if not much smaller, than without taking into account the CI principle. Therefore, coming back to the simulation argument presented earlier, it follows than we are less likely to be sims.
Critics and limitations
As a potential limitation of what we have just said, let's note that we did not take quantum randomness into account. This could make Laplace's demon impossible, as many physical events are fundamentally random, making the future state of the universe impossible to predict, even in principle and with all data and computing power needed. However, we may be justified not taking this into account, as systems with such great complexity and interactions make these effects negligeable due to quantum decoherence.
We should also note that CI may apply to our world but might not apply to the world running our simulation.
Furthermore, the principle of computational irreducibility does not entirely rule out the possibility of simulations. It merely suggests that such simulations would be less practical and less likely to be used for predicting the future in a timely manner, and reduces the incentive for advanced civilizations to run such simulations. Note that the same concern applies to the main sim-blockers. Each of them either provides arguments for a merely potential impossibility to create sims (e.g the substrate-dependence of consciousness), or merely reduces the incentive to create sims (e.g. the moral reasons). Still, the scenario in which non-sims create sims remains plausible and therefore, it remains also plausible that we are actually sims.
Kane Baker, The Simulation Hypothesis www.youtube.com/@KaneB
Bostrom, Nick (2003). "Are You Living in a Computer Simulation?". Philosophical Quarterly. 53 (211): 243–255
Chalmers DJ (2022) Reality+: virtual world and the problems of philosophy. W. W. Norton & Company, New York, NY
Functionalism (philosophy of mind) on Wikipedia https://en.wikipedia.org/wiki/Functionalism_(philosophy_of_mind)
Laplace, Pierre Simon, A Philosophical Essay on Probabilities, translated into English from the original French 6th ed. by Truscott, F.W. and Emory, F.L., Dover Publications (New York, 1951) p.4.
Rowland, Todd. "Computational Irreducibility." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. https://mathworld.wolfram.com/ComputationalIrreducibility.html
Ibid.