Very cool! I believe this structure allows expressing the "look back N tokens" operation (perhaps even for different Ns across different heads) via a position-independent rotation (and translation?) of the positional subspace of query/key vectors. This sort of operation is useful if many patterns in the dataset depend on the relative arrangement of tokens (for ex. common n-grams) rather than their absolute positions. Since all these models use absolute positional embeddings, the positional embeddings have to contort themselves to make this happen.
Oh, interesting! Can you explain why the "look back N tokens" operation would have been less easily expressible if all the points had been on a single line? I'm not sure I understand yet the advantage of a helix over a straight line.
Is there any sort of regularization in the training process, favouring parameters that aren't particularly large in magnitude? I suspect that even a very shallow gradient toward parameters with smaller absolute magnitude would favour more compact representations that retain symmetries.
Good question. I don't have a tight first-principles answer. The helix puts a bit of positional information in the variable magnitude (otherwise it'd be an ellipse, which would alias different positions) and a bit in the variable rotation, whereas the straight line is the far extreme of putting all of it in the magnitude. My intuition is that (in a transformer, at least) encoding information through the norm of vectors + acting on it through translations is "harder" than encoding information through (almost-) orthogonal subspaces + acting on it through rotations.
Relevant comment from Neel Nanda: https://twitter.com/NeelNanda5/status/1671094151633305602
The helix is already pretty long, so maybe layernorm is responsible?
E.g. to do position-independent look-back we want the geometry of the embedding to be invariant to some euclidean embedding of the 1D translation group. If you have enough space handy it makes sense for this to be a line. But if you only have a bounded region to work with, and you want to keep the individual position embeddings a certain distance apart, you are forced to "curl" the line up into a more complex representation (screw transformations) because you need the position-embedding curve to simultaneously have high length while staying close to the origin.
Actually, layernorms may directly ruin the linear case by projecting it away, so you actually want an approximate group-symmetry that lives on the sphere. In this picture the natural shape for shorter lengths is a circle, and for longer lengths we are forced to stretch it into a separate dimension if we aren't willing to make the circle arbitrarily dense.
A line is just a helix that doesn't curve. It works the same for any helix; it would be a great coincidence, to get a line.
Complete newbie question: is it possible to construct a version of these models that uses a 3 dimensional vector, instead of the 768 dimensional vector?
From the sound of it, the 768 dimensional vector is basically a constant linear transform of the three PCA components. Can we just declare the linear transform to be a constant array, and only train up the three components that appear to be the most needed? Eg generate the 768 from the PCA?
I think you probably could do that, but you'd be restricting yourself to something that might work marginally worse than whatever would otherwise be found by gradient descent. Also, the more important part of the 768 dimensional vector which actually gets processed is the token embeddings.
If you believe that neural nets store things as directions, one way to think of this is as the neural net reserving 3 dimensions for positional information, and 765 for the semantic content of the tokens. If the actual meaning of the words you read is roughly 250 times as important to your interpretation of a sentence as where they come in a sentence, then this should make sense?
This is kinda a silly way of looking at it--we don't have any reason (that I'm aware of) to think of these as separable, the interactions probably matter a lot--but might be not-totally-worthless as intuition.
@AdamYedidia This is super cool stuff! Is the magnitude of the token embeddings at all concentrated in or out of the 3 PCA dimensions for the positional embeddings? If its concentrated away from that, we are practically using the addition as a direct sum, which is nifty.
It is in fact concentrated away from that, as you predicted! Here's a cool scatter plot:
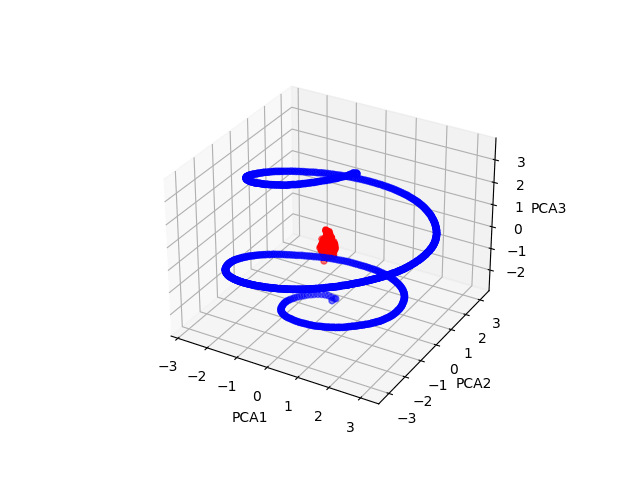
The blue points are the positional embeddings for gpt2-small, whereas the red points are the token embeddings.
If you want to play around with it yourself, you can find it in the experiments/ directory in the following github: https://github.com/adamyedidia/resid_viewer.
You can skip most of the setup in the README if you just want to reproduce the experiment (there's a lot of other stuff going on the repository, but you'll still need to install TransformerLens, sklearn, numpy, etc.
I think you could, but you'd be missing out on the 9% (for gpt2-small) of the variance that isn't in one of those three dimensions, so you might degrade your performance.
I'm pretty confused; this doesn't seem to happen for any other models, and I can't think of a great explanation.
Has anyone investigated this further?
Here are graphs I made for GPT2, Mistral 7B, and Pythia 14M.
3 dimensions indeed explain almost all of the information in GPT's positional embeddings, whereas Mistral 7B and Pythia 14M both seem to make use of all the dimensions.
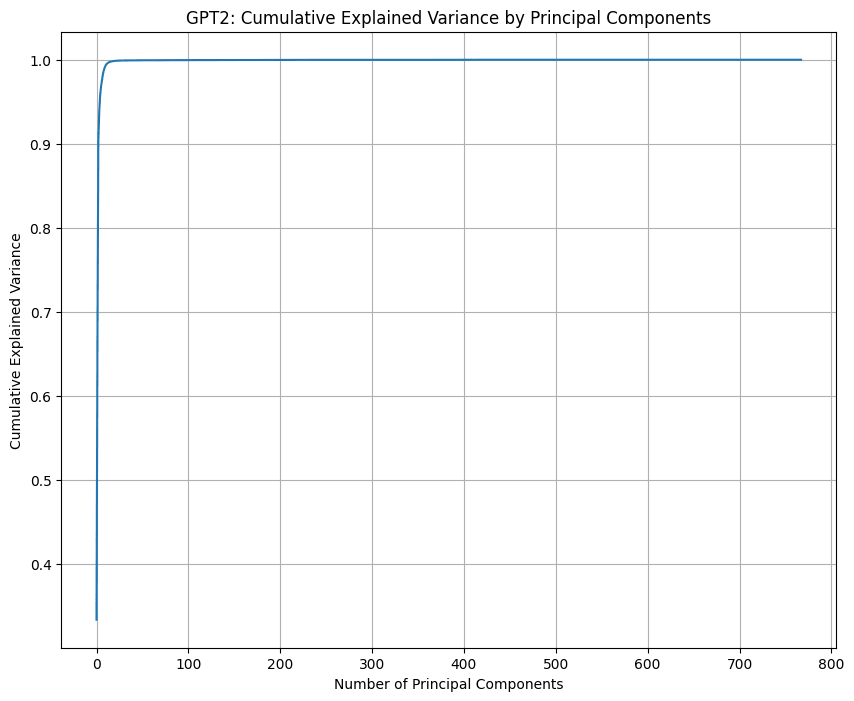
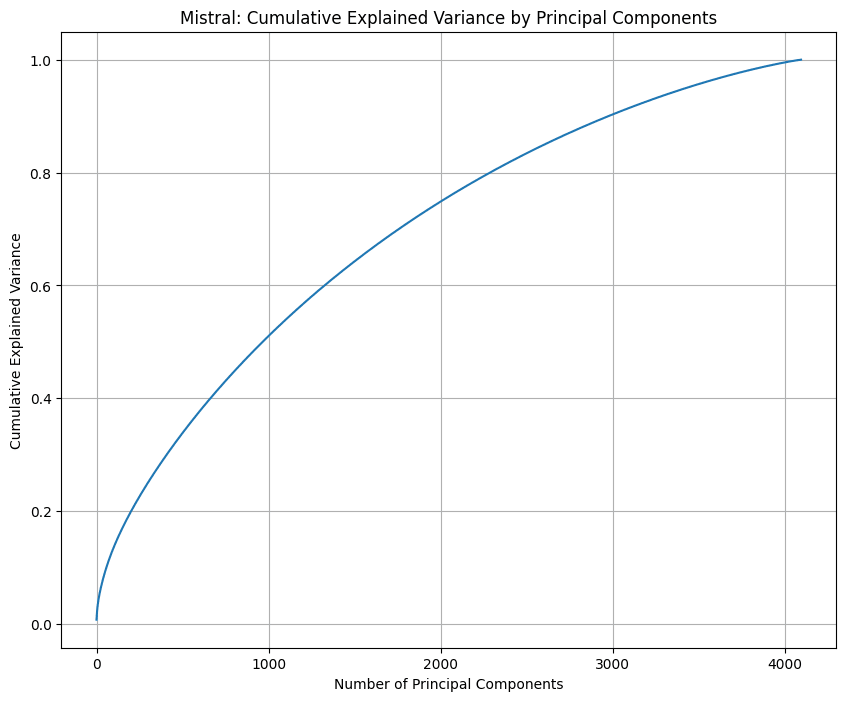
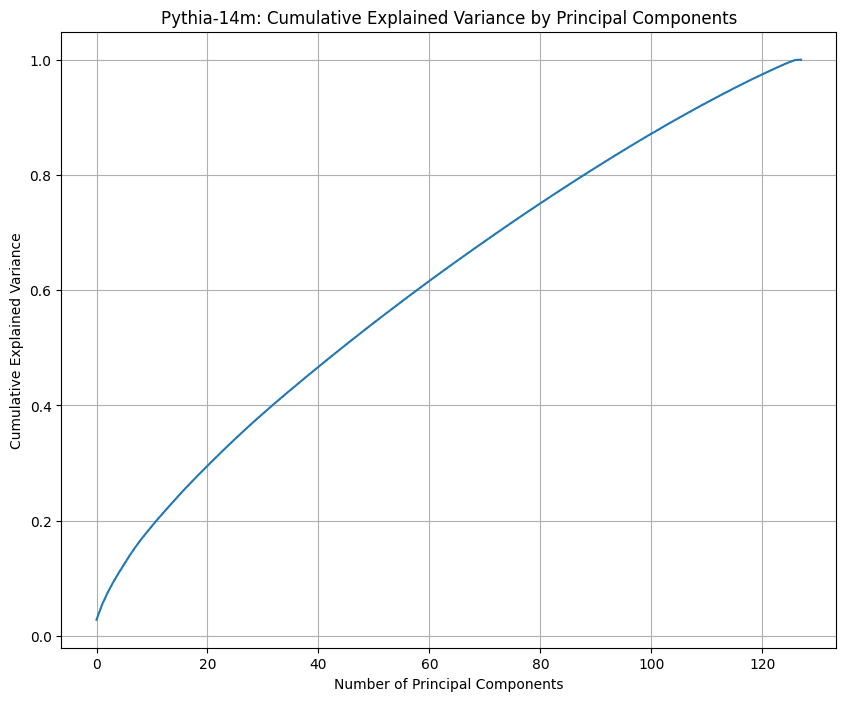
Is there something that would regularise the vectors towards constant norm? An helix would make a lot of sense in this case. Especially one with varying radius, like in some (not all) the images
It remains unexplained why this helical structure is the most natural way for GPT-2 to express position.
Just an intuition but GPT2 uses GELU function which is normalized by pi.
Btw, what visualization softwared did you use here again?
Also, what vectors are you using? is this the final output layer?
I suggest trying the vectors in the encoder layers 0-48 in GPT2-xl. I am getting the impression that the visualization of those layers are more of a submerged iceberg rather than a helix...
In the context of transformer models, the "positional embedding matrix" is the thing that encodes the meaning of positions within a prompt. For example, given the prompt:
Hello my name is Adamthe prompt would generally be broken down into tokens as follows:
['<|endoftext|>', 'Hello', ' my', ' name', ' is', ' Adam'](For whatever reason prompts to GPT-2 generally have an
<|endoftext|>token prepended to them before being fed through, to match how the model was trained.)For this prompt, the mapping of tokens to positions would be as follows:
'<|endoftext|>': 0'Hello': 1' my': 2' name': 3' is': 4' Adam': 5The positional embedding maps the positions of those tokens (0, 1, 2, 3, 4, and 5) to the meanings of those positions in vectorspace. More concretely, the positional embedding matrix maps each of those five numbers to a 768-dimensional vector of floating-point numbers, and that 768-dimensional vector gets added to a different vector that represents the semantic meaning of the token. But the first vector comes directly from the positional embedding matrix, and it is the only way the transformer has of identifying where in the prompt a given token was. So we should expect that each row of the positional embedding matrix is unique. Otherwise, two different positions would be mapped to the same vector, and the transformer would have no way of knowing which of those two positions a given token was in!
There are 1024 rows in the positional embedding matrix; this is because there are 1024 possible positions in the prompt, and each possible position gets its own row.
We should also expect that the different 768-dimensional vectors live in a low-rank linear subspace, which is just a fancy way of saying a line or a plane or something like that. After all, if you were a human engineer designing a transformer from scratch, you might devote just one of the 768 entries in each vector to encode the position—for example, you might use the first entry of each vector for this purpose, and make it be a 0 if the token was in position 0, 1 if it was in position 1, 2 if it was in position 2, and so on, and then you'd have the other 767 entries to use to encode the semantic meaning of each token, without interfering with your encoding of the token's position. Then, in vector-space, the whole positional embedding matrix would lie on a single line—the line of points where the first coordinate of each point was an integer between 0 and 1023, and every other coordinate of each point was 0. To instead use half the vector (for example) to encode the token's position would be very wasteful—you don't need that many entries in the vector just to encode a single integer between 0 and 1023.
The model, of course, was produced by a training algorithm, and so does something weirder than what a human would do. The 768-dimensional vectors mostly live in a low-rank linear subspace; there's a little bit of them that lives outside that linear subspace, but a three-dimensional subspace is enough to explain 90% of the variance over vectors in gpt2-small. We can use a technique called Principal Components Analysis (PCA) to find that three-dimensional subspace. When we graph each vector in the positional embedding matrix as a single point in the three-dimensional subspace, we get a helix:
In this plot and all plots that follow, I omit position 0, because it's always an outlier; that position is the position of the
<|endoftext|>token that gets prepended to every prompt and it has its own weird stuff going on. The dark blue end of the helix is the vectors of the first positions in the prompt; the dark red end of the helix represents the vectors of the last positions in the prompts. Interestingly, we can see that the very last position, position 1023, is an outlier as well; I don't understand why that would be.This result is pretty consistent across the various different GPT-2 models, including the Stanford ones; here's the equivalent plot for all 9 GPT-2's on TransformerLens:
We get a clear helix in all but gpt2-xl (the middle-left plot). I'm not sure why that one is so different; it's still a little helix-like, but a lot less than the 8 others. Interestingly, there's some qualitative differences between OpenAI's four GPT-2's and the five GPT-2's from Stanford; more of the variance in the positional embedding matrix can be attributed to a three-dimensional subspace in OpenAI's models than Stanford's; Stanford's helices are "shakier"; and Stanford's helices have more loops in them than OpenAI's. I don't know where these qualitative differences come from; presumably something about how they were trained. I know that Stanford's were trained on OpenWebText whereas OpenAI's were trained on a private-but-reproducible other dataset, but I don't know of other differences.
We can see some amount of "fraying" in the OpenAI helices on the blue end; this implies that maybe the earliest vectors in the positional embedding matrix are relying on a different subspace than all the others. To check this, I tried truncating out the first 100 vectors (so just looking at the 924 vectors corresponding to positions 100 through 1023).
This makes a big difference to the OpenAI models, getting rid of all the "fraying" and substantially increasing the percent variance explained of the 3D subspace found. It makes very little difference to the Stanford models.
In contrast, if we look at a PCA over just the first 100 positions, this is what we see:
(Note that the 3D space we're looking at isn't the same each time; every time we pick some subset of the vectors to look at, we're finding the "best" 3D subspace for just that set of vectors. That's why this plot doesn't just look like a "zoomed-in" version of the previous plots.)
We can see from these that the OpenAI models really seem to care a lot about the first few tokens and "differentiate" those tokens more by spacing them out. (Who even knows what's going on with the Stanford models here! I'm confused by those plots.)
Some people observed parts of this helical structure over the positional embedding matrices previously; for example, this reddit post notes that many of the entries of the vectors in the pos-embed matrix taken in isolation make something that looks kind of a sine wave. And Lukas Finnevden noticed a periodic pattern to the cosine similarity between rows of the positional embedding matrix (thanks to Arthur Conmy for pointing this out!).
Both of these observations are explained by the helical structure of the positional embedding matrix.
It remains unexplained why this helical structure is the most natural way for GPT-2 to express position. Maybe something about the structure of transformers makes it very easy to encode information as circular patterns? Neel Nanda's Grokking Modular Arithmetic found that a trained network learned to use trigonometric functions to perform modular arithmetic—but that could just be a coincidence, since modular arithmetic seems more clearly related to periodic functions than the positions of tokens in a prompt.